基于分位數回歸的金融風險度量

張 成，周炳均，鄭 興

（西南交通大學 數學學院，成都 611756）

引言

2007年8月，美國次貸危機爆發，進而引發全球金融危機，全球金融系面臨自1929年以來的最大危機。此外，近二十年內國際金融市場的劇烈波動以及金融危機在全世界范圍內頻頻發生，如1992年的貨幣危機、1994年墨西哥金融危機、1997年亞洲金融危機等。同時，一些大的金融機構也經常因為不完善的風險管理而遭受巨大的損失甚至破產，如英國巴林銀行破產案、中航油新加坡等。上述金融事件的頻頻發生，說明現在經濟全球化不斷加深的時代，對金融風險的管理已經成為金融機構必須注重考慮的問題，因此，對于金融風險管理的研究顯得異常的重要。

由于風險價值（VaR）具有定量性、綜合性、直觀性等優點，能夠直觀定量地給出單個資產或者資產組合綜合的風險值，逐漸發展成為金融風險管理中最常用也是最有效的方法，國內外學術界對VaR模型的研究也越來越流行和深入。張堯庭（1998）、鄭文通（1999）等介紹了VaR方法的產生背景、定義、計算方法、用途以及引入中國的必要性[1~2]；肖春來等（2003）在股票價格和收益率服從二元正太分布的假設下，提出一種計算條件VaR的方法[3]；蘇濤（2007）對金融市場風險VaR度量模型進行了改進研究[4]。

分位數回歸理論由Koenker和Bassett提出[5]，其特點是描述在不同變化范圍和條件分布形狀下自變量對因變量的影響。分位數回歸適應了尖峰厚尾這種金融事件序列常見統計特征，并且能夠較好地描述尾部特征。自從分位數回歸的理論提出之后，國內外學者開始將分位數回歸理論應用在教育、工資收入、需求分析、經濟學等其他廣泛領域。段景輝、陳建寶（2009）用分位數回歸對我國城鄉家庭收入差異影響因素進行了解析[6]；段玉（2011）用分位數回歸對湖南省城鄉居民收入與消費需求進行了分析[7]。在金融領域，Taylor（1999，2000）構造持有期為k的分位數回歸VaR模型[8~9]；Engle和Manganeli（2004）首次提出了分位數條件自回歸模型（CAViaR）[10]；關靜、史道濟（2008）選取適當的尾部分位數回歸方法，模擬預測了極端水平下上證指數收益率的條件VaR[11]；張海云（2011）研究了基于分位數回歸的股指期貨風險度量[12]。

本文利用分位數回歸思想，結合GARCH參數模型，用分位數回歸方法估計回歸參數，計算VaR，并與GARCH模型計算的VaR結果進行比較。

一、分位數回歸基本原理

對于線性模型yt=X'β+ut，其中X，β都是p×1維向量。則分位數回歸模型如下：

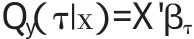
其中，Q（yτ|x）=inf{y：Fy（y|x）≥τ}表示y的分位數為模型中參數β的估計值。如果τ=1/2，回歸模型即為中位數回歸稱作中位數回歸系數估計量。

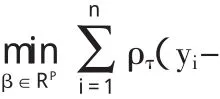
二、GARCH Quantile風險度量模型基本原理

根據Bollerslev提出的GARCH模型，可以得到與之等價的廣義GARCH模型結構如下：

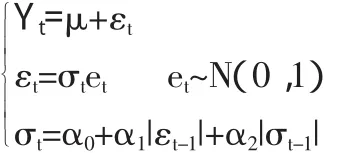
本文將分位數回歸與廣義GARCH模型結合，用GARCH Quantile風險度量方法計算上市公司A股在險價值VaR。

如果給定一個分位數水平τ，則殘差的分位數函數為：

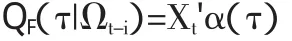
其中，QF（τ|Ωt-i）=inf{y：Fy（yt|Ωt-i）}表示殘差分布F的的τ分位數。如果Yt表示對數收益率，則可得到置信水平為1-τ的VaR為：

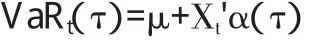
其中，Xt=（1，|εt-1|，|σt-1|）'，α（τ）=α0QF（τ），α1QF（τ），α2QF（τ））'，QF（τ）是殘差分布F的τ分位數函數；此模型即為GARCH Quantile風險度量模型表達式。α（τ）可以通過非線性分位數回歸對其進行參數估計：

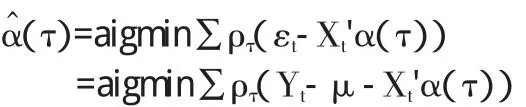
三、實證分析

本文數據選取江蘇國泰（股票代碼：002091）2012年9月18日至2014年3月31日共365個收盤價數據，股票收益率定義為Rt=lnPt-lnPt-1。

首先作收益率序列折線圖（見下圖）。

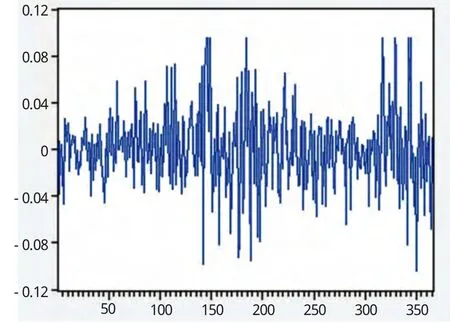
收益率序列折線圖

從下圖中可以看出，江蘇國泰股票收益率基本上在零值附近上下波動，隨著時間的改變收益率也在不斷的改變。從收益率散點圖上可以發現，收益率序列總體上是平穩的，并且會在一段時間內集體的偏高或偏低，即收益率波動的集簇性。可用GARCH模型對收益率數據進行建模擬合。

應用GARCH（1，1）分別在正態分布和t分布下對收益率序列建模，波動方程參數估計結果（見表1）。

表1 N-GARCH（1，1）模型和 t-GARCH（1，1）模型參數估計結果

有參數估計結果可以得到計算收益率序列波動率的表達式，再由VaR的計算公式VaR=Zασt得到VaR的值，其中Zα是GARCH模型中殘差分布Z的下α分位點，t表示持有期，本文中持有期為t=1天。由于波動率σt是一列時間序列，故本文通過公式計算的VaR也是時間序列。分別計算置信水平95%和99%水平下的VaR，結果（見表2）。

表 2 N-GARCH（1，1）模型和 t-GARCH（1，1）模型計算 VaR 結果

應用分位數回歸思想廣義GARCH模型結合的GARCH-Q 模型分別計算置信水平為95%和99%的VaR，建立分位數回歸模型：

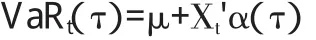
模型參數估計結果（見表3）。

將參數估計結果代入分位數回歸方程即可求得VaR值。由模型表達式可以看出VaR依賴于廣義GARCH模型均值方程殘差滯后項的絕對值以及波動率滯后項的絕對值，故由GARCH-Q模型計算的VaR也是一列時間序列。在不同置信水平下的計算結果（見表4）。

表3 兩種GARCH-Q模型參數估計結果

表4 兩種GARCH-Q模型在95%置信水平下VaR計算結果

對VaR的精確事后檢驗，最常用的的是Kupiec（1995）提出的失敗率檢驗法。其基本思想是，將實際損失超過VaR的記為失敗，用失敗天數除以總觀察天數得到失敗率，將失敗率與預先設定的VaR顯著性水平作比較，越接近則表明VaR模型預測效果越好。

假設將觀察的結果看做是一系列的獨立伯努利試驗，失敗的期望概率為α（1-α為置信水平）。假定實際觀察天數為T，失敗天數為N，則失敗率為p=N/T。原假設為 H0：p=α，Kupiec提出使用似然比檢驗做假設檢驗，LR統計量為：

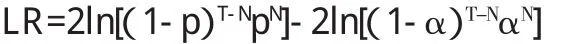
若VaR模型正確，則LR統計量漸進服從χ2（1）分布。LR統計量的值越小，越不能拒絕VaR模型正確的原假設，即LR統計量值越小說明模型預測越準確。

將各個模型在95%置信水平下的失敗率情況整理（見表5）。

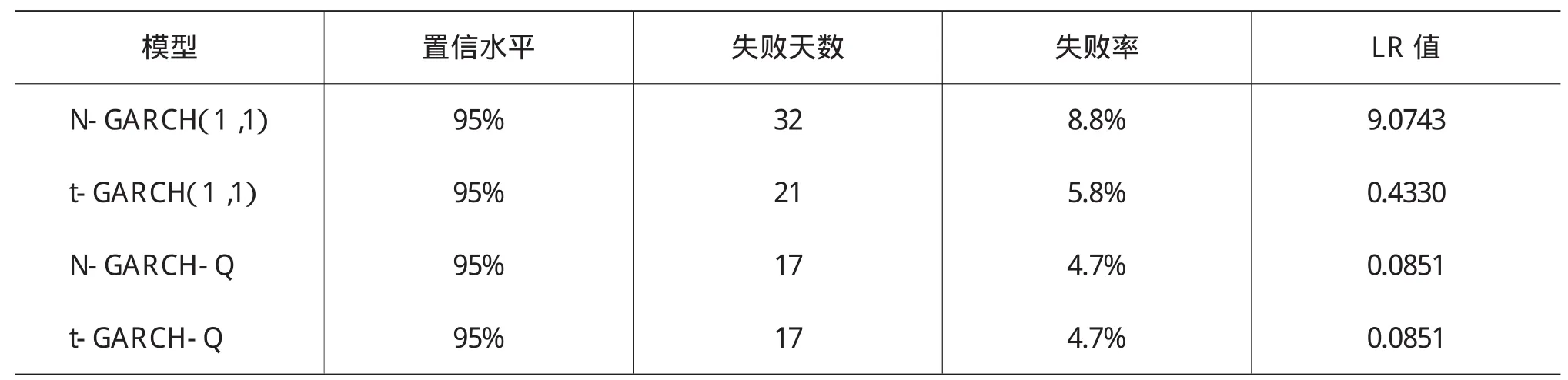
表5 各個模型計算得到的VaR失敗率整理

根據失敗率檢驗法原理，在5%的顯著性水平下自由度為1的卡方分布檢驗在5%的顯著性水平下臨界值為3.8415，在不拒絕原假設前提下，VaR的優劣判斷遵循LR最小準則。從表5結果看，N-GARCH模型置信度為95%的水平下計算VaR的LR值為9.0743，在統計意義下拒絕原假設，可以認為N-GARCH模型計算的VaR不準確，即與實際風險狀況不符。而t-GARCH模型的LR值為0.4330，不拒絕原假設，可認為t-GARCH模型是比較合理的VaR預測模型。而在95%的置信水平下，N-GARCH-Q模型和t-GARCH-Q模型的LR統計量值都是0.0851，遠遠小于兩個GARCH模型的LR值。這說明分位數回歸GARCH模型（GARCH-Q模型）計算VaR比GARCH模型計算的VaR值更加精確，更能夠反映股價波動為投資收益帶來的風險情況。

值得注意的是，N-GARCH-Q模型和t-GARCH-Q模型兩個模型的失敗天數、失敗率和LR統計量值都相等，這體現了分位數回歸計算VaR時最突出的優點，即分位數回歸計算VaR時，不會受收益率分布的影響。也就是說，用分位數回歸進行風險度量，計算VaR時，不需要對收益率的分布做假設，這是分位數回歸相對于其他風險度量方法的最重要的優點。

結論

結合以上結果分析可以得出以下基本結論：

1.從整體上看，GARCH模型計算VaR時，對單只股票或者投資組合的風險判斷上存在明顯的低估現象，對于市場出現劇烈波動時，很難捕捉到市場因子急劇變化對風險的影響。

2.基于分位數回歸思想和GARCH模型結合的GARCH-Q模型，能夠準確地預測股票或投資組合的在險價值VaR，能夠精確地刻畫市場波動時的風險狀況，有效地

克服了GARCH模型低估市場劇烈波動風險的缺點。在風險測量上GARCH-Q模型比GARCH模型具有更加優良的性質和更加準確的度量能力，是更為有效的方法。

3.應用分位數回歸計算VaR時，結果不受收益率分布假設的影響，即用分位數回歸思想計算VaR時，可以不用對收益率分布做假設。

[1]鄭文通.金融風險管理的方法及其應用[J].國際金融研究，1999，(9)：23-26.

[2]張堯庭.金融市場的統計分析[M].南寧：廣西師范大學出版社，1998.

[3]肖春來，柴文義，楊威.條件VaR理論的應用與研究[J].數理統計與管理，2003，(22)：264-268.

[4]蘇濤.金融市場風險VaR度量方法的改進研究[D].天津：天津大學博士學位論文，2007.

[5]Koenker R.Bassett G J.Regression Quantiles[J].Econometrical，1978，(46)：3-50．

[6]陳建寶，段景輝.中國性別工資差異的分位數回歸分析[J].數量經濟技術經濟研究，2009，(10)：87-97.

[7]段玉.基于分位數回歸的城鄉居民收入與消費需求分析[J].求索，2011，(11)：45-47.

[8]Taylor，A Quantile Regression Approach to Estimating the Distribution of Multi-Period Returns[J].Journal of Derivatives，1999，(7)：64-78.

[9]Taylor，A Quantile Regression Neural Network approach to Estimating the Conditional Density of Multi-Period Returns[J].Journal of Forecasting，2000，(19)：299-311.

[10]Engle R.F.and Manganelli S，CAViaR：conditional autoregressive value at risk by regression quantiles[J].Journal of Business and Economic Statistics，2004，(22)：367-381.

[11]關靜，史道濟.基于分位數回歸模型的滬深股市風險測量研究[J].統計與信息論壇，2008，(12)：15-19.

[12]張海云.論分位數回歸在計算VaR中的應用[J].現代商貿工業，2011，(15)：185-186.