導線舞動對輸電桿塔作用的試驗技術*

楊曉輝， 樓文娟， 陳貴寶， 呂中賓

(1.國網河南省電力公司電力科學研究院 鄭州，450052) (2.浙江大學建筑工程學院 杭州，310058) (3.上海交通大學電氣工程系 上海，200030) (4.國網河南省電力公司信陽供電公司 信陽，464000)

?

導線舞動對輸電桿塔作用的試驗技術*

楊曉輝1，3， 樓文娟2， 陳貴寶4， 呂中賓1

(1.國網河南省電力公司電力科學研究院 鄭州，450052) (2.浙江大學建筑工程學院 杭州，310058) (3.上海交通大學電氣工程系 上海，200030) (4.國網河南省電力公司信陽供電公司 信陽，464000)

基于輸電桿塔的實際結構特點及線路舞動發生的不確定性，在實際輸電線路上開展桿塔的舞動承載特性測試難度較大。以實際舞動損壞的500 kV典型桿塔為原型，采用基于相似理論的結構建模方法實現了輸電塔線體系的實驗室節段建模，利用機械加載的方式實現舞動載荷的模擬，并在此基礎上搭建了相應的數據采集和分析系統，能夠實現輸電桿塔的舞動響應特性測試。利用該試驗系統，分別進行了舞動幅值、頻率變化對輸電桿塔動態承載特性的影響分析。結果表明,該試驗系統能夠對輸電桿塔的舞動承載特性進行模擬分析。

輸電線路; 舞動; 桿塔; 相似理論; 結構建模; 動態響應特性; 試驗技術

引 言

輸電線路長時間舞動除造成電氣跳閘、線路停電外，還容易造成導線、桿塔受損等難以直接恢復的機械性破壞，在增加線路運行維護成本的同時，對電網供電的可靠性也帶來了很大影響[1]。通過對近10年來全國范圍內舞動所造成的桿塔損壞事故統計分析發現，舞動造成機械損壞的輸電桿塔數量巨大、個別嚴重的甚至出現了倒塔現象[2]。

自20世紀30年代觀測到輸電線路舞動以來，國內外科研機構和學者便對其開展了深入研究，從舞動發生機理及其成因、舞動特性分析到防舞動措施研究等[3-7]，對輸電線路舞動防治工作起到了一定的促進作用，但對于輸電桿塔的舞動承載特性及其受損原因鮮有涉及。在舞動問題的研究中經常將輸電桿塔簡化為導線的固定支座，忽略了輸電桿塔的影響。目前，關于輸電桿塔的振動特性及其安全性能分析主要依靠數值分析[8-9]，造成這一局面的主要原因有：a．桿塔結構高大、聯接復雜，開展實際輸電桿塔的舞動承載特性測試時，需要布置的測點數量龐大、系統復雜；b．實際線路舞動的發生具有一定的偶然性和隨機性，無法預測具體某個線路段何時會發生舞動。綜合考慮這些因素，利用實際輸電線路桿塔開展舞動承載特性的研究不具有可行性。

基于相似理論的結構建模方法，主要是通過相似定理和固定邊界條件的方法來對“原型”進行建模，在保持“模型”和“原型”相似的前提下，由模型試驗結果推算出原型結構的相應結果，這一建模和問題求解方法在工程結構方面得到了廣泛應用[10]。考慮到輸電桿塔的構件材料為各向同性的鋼材、導線舞動同樣滿足牛頓運動方程，可以采用結構相似的建模方法來對輸電桿塔的舞動承載特性進行分析。

現以500 kV開祥線的實際舞動事故為例，基于結構相似理論和子結構建模法搭建了輸電塔線體系的實驗室模型，通過動力加載裝置模擬不同舞動載荷下的桿塔承載特性測試分析，為輸電桿塔的抗舞性能及其損壞模式研究提供了研究手段和基礎數據。

1 輸電塔線體系的實驗室建模

1.1 試驗建模的相似準則

根據導線舞動特征，輸電鐵塔在導線舞動作用下的運動方程[11]可以表示為

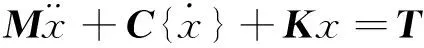
(1)

其中：M為輸電塔的質量矩陣；C為阻尼矩陣；K為剛度矩陣；x為位移；T為導線舞動時傳遞到輸電塔上的張拉力。

根據鋼結構特點可知：輸電塔的質量與材料密度ρ和構件尺寸L有關，桿塔剛度則與材料彈性模量E和桿件尺寸L有關。因此在制作縮比模型時，可取ρ，E，L為基本量，其他物理量均可以表示為基本量的冪次單項式[12]。因此式(1)可改寫為

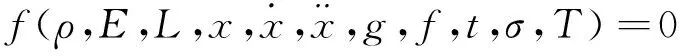
(2)

其中：g，f，t分別為重力加速度、頻率和時間。

將式(2)的物理參數均表示為無量綱參數，可改寫為

(3)

根據量綱和諧的原則，由式(3)可以得出

[1]=[ρ]a1[E]a2[L]a3[L]a4[E0.5ρ-0.5]a5· [Eρ-1L-1]a6[Eρ-1L-1]a7[E0.5ρ-0.5L-1]a8· [E-0.5ρ0.5L]a9[EL2]a10[E]a11

(4)

(5)

由此可知，在結構建模過程中各物理量相似參數能夠滿足上述8個相似準數的條件，則所建試驗模型能夠模擬原輸電桿塔結構的動力響應特性。

1.2 輸電桿塔建模

舞動事件中，實際受損的500 kV開祥線#27桿塔型號為5D-SJ4,桿塔實際高度為54.5 m(其中呼稱高為24 m，塔頭部分30.5 m)，主要造成了塔頭部分中橫擔的破壞。在試驗建模時，選定包含各橫擔的塔頭進行節段建模和試驗研究，如圖1所示。

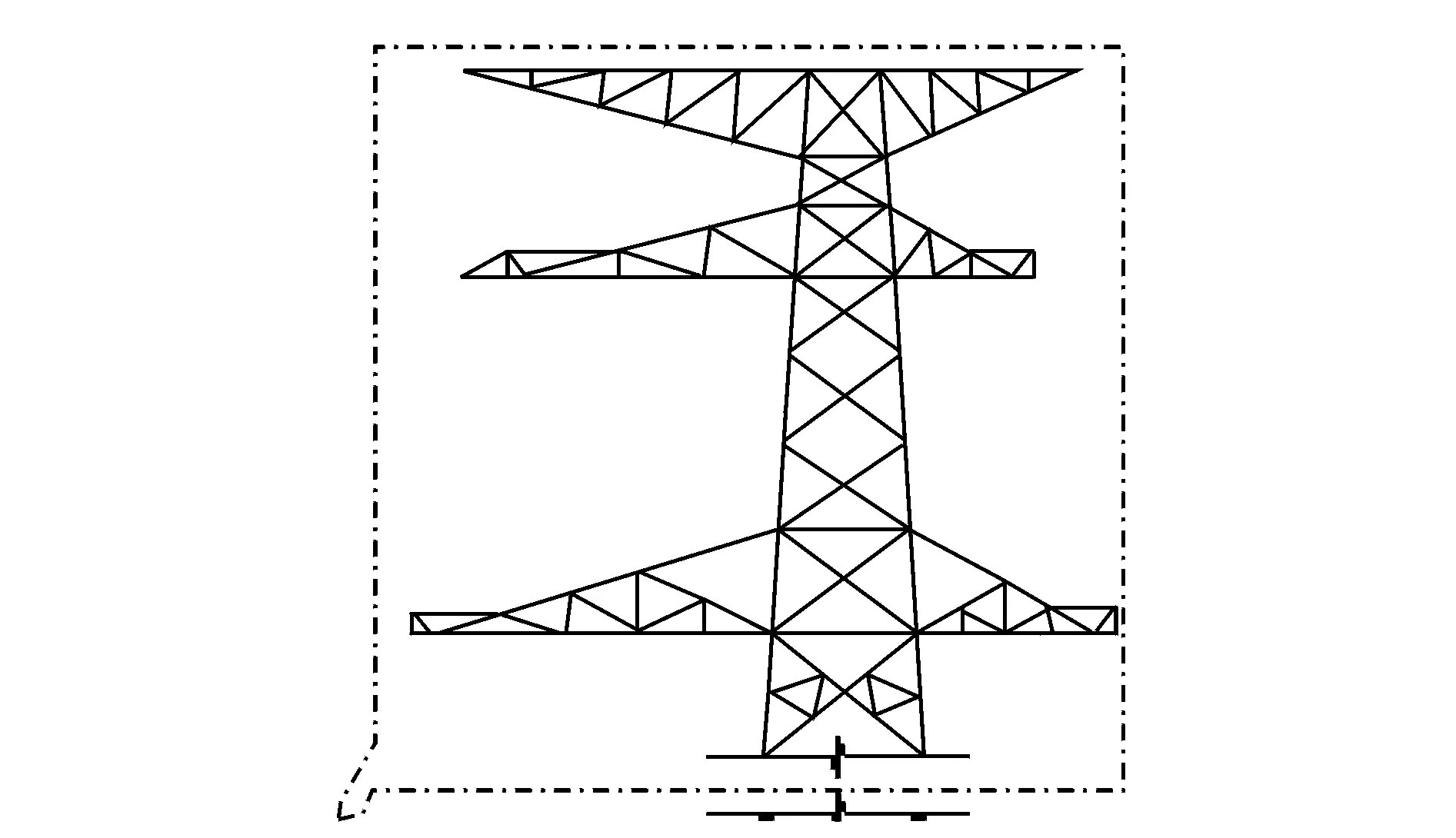
圖1 輸電鐵塔的節段模型Fig.1 The section model of tower

設定輸電塔節段模型的尺寸相似系數為CL=1∶4；制作模型的材料仍然選定為鋼材，彈性模量相似系數CE=1∶1，按照不考慮重力相似的準則考慮，選擇Cρ=1∶1。以式(5)計算得出輸電桿塔張力、應力以及表征其運動特征的頻率、位移、速度和加速度等參數的相似系數。

考慮到輸電桿塔振動時慣性力對構件內力的影響及其所需滿足的動力相似關系，節段模型的支座設計為彈性支座，用以模擬桿塔下半部分的整體剛度。在實際舞動過程中，輸電桿塔下半部分所要承受的外載荷是導線舞動時的動態張拉力，作用在桿塔上時可以視作是壓力和拉力兩種形式的組合。因此，在彈性支座組裝時采用模具彈簧組合并結合螺栓預壓的方式來實現。

1.3 覆冰導線建模

在輸電線路的實際運行過程中，導線覆冰存在一定的不確定性，覆冰厚度及形狀與當時的氣象條件有關[13]。因此在進行覆冰導線建模時，不僅要考慮導線模型與原型之間的相似關系，還需要對導線在不同覆冰狀態下的建模進行考慮。

在覆冰導線建模時，重點考慮導線等效截面積及其重力作用的影響，對導線的分裂數及結構特征忽略不計。選擇外徑為12 mm、型號為7×19不銹鋼鋼絲繩模擬實際輸電導線，對其表面的覆冰模擬則是通過調整設置在導線上的配重塊來實現，即：不同覆冰條件下所設置的配重塊數量不等。在實際使用過程中配重塊沿導線方向均勻布置。 輸電塔線體系的實驗室建模如圖2所示。

圖2 輸電塔線體系的實驗室建模Fig.2 The laboratory model of tower-line system

2 舞動加載及測試技術

2.1 模擬舞動的動力加載技術

由于主要目的是對輸電桿塔的舞動響應特性進行試驗研究，試驗關鍵技術之一是如何再現覆冰導線舞動時產生的動態張拉力。因此試驗過程中對舞動載荷的模擬 可以通過機械加載的方式實現。

有關舞動的現場觀測和前期研究表明：覆冰導線舞動時，運動軌跡為豎向幅值大、橫向幅值小的橢圓或者類橢圓，頻率為導線豎向某個階次的自振頻率[13]。在舞動加載裝置設計時，采用以豎向振幅為半徑的圓形軌跡對導線進行激振，激勵幅值的大小按照相似系數和導線實際舞動幅值進行換算，激勵通過電機驅動的機械裝置實現。

為了檢驗導線跨中在圓形軌跡的激勵狀態下能否產生與導線舞動時相似的動態張拉力變化效果，首先通過數值模擬的方式對其激振效果進行了計算,兩種情況下的導線水平向張力變化對比見圖3。

通過與計算結果的對比分析發現：在沿導線方向上的動張力時程能夠較好吻合，相應的功率譜和特征頻率也具有較好的一致性。

圖3 導線水平向張力變化對比圖Fig.3 Comparison of conductor tension in horizontal direction

2.2 測試系統的搭建與測點布置

根據桿塔動態承載特性的測試，在對輸電桿塔的舞動響應特性試驗中，主要測試數據包括導線張拉力、加速度響應以及桿塔構件應變。其中：導線張拉力通過在試驗導線與桿塔掛點之間串接拉力傳感器的方式進行測量；桿塔加速度采用電荷式加速度傳感器，分別在中橫擔端部、橫隔及其塔頂等位置進行布點測量；桿塔應變采用電阻應變片，選擇帶溫度補償特征的半橋電路測量方法，重點在關鍵部位的受壓和受拉桿件上布點測量。整體的信號采集系統選用TST5912動態信號分析儀進行測量和記錄，為了確保測試系統能夠實現試驗數據的準確、可靠測量，信號采集回路還配置有專門的應變適配器和電荷適配器，用來轉換和放大拉壓力傳感器和應變片采集到的電信號。試驗系統整體如圖4所示。

圖4 測試系統中張力傳感器安裝位置Fig.4 Sensor position for measuring conductor tension

3 桿塔舞動響應特性測試

同等導線覆冰與舞動半徑條件下、不同舞動頻率時輸電桿塔的舞動響應特性見圖5。

圖5 不同舞動頻率時的桿塔響應特性(冰厚0.75 D、舞動半徑15 cm)Fig.5 The dynamic response with different galloping frequency (ice-thickness 0.75 D, vibration diameter 15 cm )

通過舞動頻率變化對輸電桿塔舞動響應特征值的影響可以看出：所有特征參數的幅值對舞動半徑變化呈線性變化；而隨舞動頻率的變化特征則較為復雜，其中加速度對頻率變化較為敏感，導線張力和桿件應變對舞動頻率的變化反應不是很明顯。由此可以得出：舞動幅值對桿塔舞動承載特征的影響要大于頻率的影響。利用該試驗系統，還可以進行舞動事故的反演。根據舞動現場觀測到的覆冰厚度和舞動幅值進行參數調整，用以分析輸電桿塔在導線舞動作用下會發生何種原因的強度損壞。

4 結束語

利用相似理論的結構建模方法，以實際舞動受損的500 kV輸電塔線體系為原型，筆者搭建了塔線體系的縮比模型，并通過相應的激振裝置來模擬實現導線舞動加載，搭建了輸電桿塔舞動響應特征的試驗系統。基于現有的傳感技術，搭建了相應的信號采集與測試系統。利用搭建的輸電塔線舞動響應特性測試系統，能夠根據現場實測的舞動特征參數來對實際輸電線路舞動時桿塔受力狀況進行模擬分析，同時還具備開展舞動特征參數變化對輸電桿塔動態響應特性影響的試驗功能研究。為開展舞動條件下的輸電桿塔承載特性及其損壞模式的研究，提供了試驗方法和條件。

[1] 王少華，蔣興良，孫才新，等．輸電線路導線舞動的國內外研究現狀[J].高電壓技術，2005,31(10)：11-14.

Wang Shaohua, Jiang Xingliang, Sun Caixin, et al. Study status of conductor galloping on transmission line[J]. High Voltage Engineering,2005,31(10):11-14. (in Chinese)

[2] 盧明,孫新良,閻東.500 kV姚邵線舞動倒塔事故分析及對策[J].電瓷避雷器,2008(3):1-5.

Lu Ming, Sun Xinliang, Yan Dong. Cause of Conductor Galloping Tower Collapse at Yaoshao 500 kV Transmission Line[J]. Insulators and Surge Arresters, 2008(3):1-5. (in Chinese)

[3] Nojima T, Shimizu M, Ogi I, et al. Development of galloping endurance design for extra-large 6-conductor bundle spacers by the experience of the full scale 500 kV test line[J]. IEEE Transactions on Power Delivery, 1997,12(4):1824-1829.

[4] Wang Jeff. Overhead conductor vibrations and control technologies[C]∥2006 International Conference on Power System Technology. Chongqing, China: IEEE, 2006: 1-5.

[5] 李新民，朱寬軍，李軍輝．輸電線路舞動分析及其防治方法研究進展[J].高電壓技術,2011,37(2):484-490.

Li Xinmin, Zhu Kuanjun, Li Junhui. Review on analysis and prevention measures of galloping for transmission line[J]. High Voltage Engineering, 2011,37(2):484-490. (in Chinese).

[6] Gurung C B, Yamaguchi H, Yukino T. Identification of large amplitude wind-induced vibration of ice-accreted transmission lines based on field observed data[J]. Engineering Structures, 2002,24(2):179-188.

[7] Lilien J L, Vinogradov A A. Full-scale tests of torsional damper and detuner (TDD) antigalloping device[J]. IEEE Transactions on Power Delivery, 2002,17(2):638-643.

[8] 楊靖波，李正．輸電線路鋼管塔微風振動及其對結構安全性的影響[J]．振動、測試與診斷，2007,27(3):208-211.

Yang Jingbo, Li Zheng. Breeze vibration of transmission steel tubular tower and its effects on structure safety[J]. Journal of Vibration , Measurement & Diagnosis, 2007,27(3):208-211. (in Chinese)

[9] 田利，李宏男，周海鷹．空間變化地震動下輸電塔-線體系振動控制研究[J]．振動、測試與診斷，2013,33(3):369-377.

Tian Li, Li Hongnan, Zhou Haiying. Study on vibration control of transmission tower line system under the vibration of space[J]. Journal of Vibration, Measurement & Diagnosis,2013,33(3):369-377. (in Chinese)

[10]陸瑋,盧文勝,胡錫勇．整體結構模型材性相似調整[J]．結構工程師,2012,28(1)：45-49.

Lu Wei, Lu Wensheng, Hu Xiyong. Similarity adjustment approaches of structure models based on material properties[J]. Structure Engineers, 2012,28(1):45-49. (in Chinese)

[11]Ray Clough， Joseph Penzien．結構動力學[M]．王光遠，譯校．北京：高等教育出版社，2006：140-159.

[12]楊俊杰．相似理論與結構模型試驗[M]．武漢：武漢理工大學出版社，2005：18-22．

[13]郭應龍,李國興,尤傳永．輸電線路舞動[M]．北京:中國電力出版社,2003：103-107.

10.16450/j.cnki.issn.1004-6801.2015.05.028

2013-08-10；

2013-12-13

TM726

楊曉輝，女，1982年9月生，高級工程師。主要研究方向為輸電線路舞動試驗技術與輸變電設備性能檢測。曾發表《500 kV六分裂導線舞動時的動張力變化特征》(《上海交通大學學報》2014年第38卷第9期)等論文。 E-mail:yangxiaohuisoso@163.com