基于CNS性能的飛行間隔安全評估*
賀文紅
(北京西三環中路19號 北京 100071)
?
基于CNS性能的飛行間隔安全評估*
賀文紅
(北京西三環中路19號 北京 100071)
為了有效地確定自由飛行下航空器之間的安全間隔,論文研究了基于通信、導航、監視性能的安全飛行問題。通過分別對所需通信性能、所需導航性能和所需監視性能進行分析,結合概率論相關知識建立了航空器之間的碰撞風險模型,并對不同飛行速度和飛行間隔情況下的碰撞風險進行了計算分析。結果表明兩機水平間隔越大,碰撞概率越小;兩機連線的飛行速度分量越大,所需的最小安全間隔越大。
空中交通管理; CNS性能; 飛行間隔; 碰撞風險
Class Number V321
1 引言
隨著航空運輸業的發展,我國的航空技術的不斷進步,空中交通流量逐漸增大,空域日益擁擠。安全是民航的永恒主題,為了增加空域容量,滿足流量需求,保障空中交通的安全有序,有關間隔安全評估的研究是必不可少的。
為促進空中交通管理系統在全球范圍內的互用性和互通性,國際民航組織(ICAO)在推薦新的通信、導航、監視和空中交通管理系統技術的同時,一直在探索“所需性能”概念的建立與應用。因此提出了基于性能的通信導航監視(CNS)系統,其由所需通信性能(RCP)、所需導航性能(RNP)和所需監視性能(RSP)組成。國內外很多理論研究者從碰撞風險入手,通過建立碰撞風險模型來對飛行間隔的安全進行評估,因此在CNS環境下如何保證飛行安全成為一個研究熱點。
在歐美等航空業發達國家,安全間隔方面的理論工作從20世紀60年代就已經開始進行了,最著名的是英國的Reich在20世紀60年代針對北大西洋地區平行航路系統在縱向、側向和垂直方向分別建立了碰撞風險模型[1~3]。Peter Brooker分別提出了縱向間隔和側向間隔的EVENT碰撞風險模型[4~5]。目前對于CNS性能環境下的碰撞風險研究處于起始階段,國內有一些研究者已經開始對其進行研究,張兆寧、沈金煒等利用Reich模型和概率論的知識提出了CNS環境下的平行航路碰撞風險模型[6~8]。
本文對CNS性能下飛機的飛行間隔安全評估問題進行了探索研究,對同高度飛行情況下如何根據安全目標水平及CNS性能環境來設定相應的飛行間隔,建立了同高度飛行條件下基于CNS定位誤差的碰撞風險模型,并利用Matlab對不同飛行速度和飛行間隔情況下的碰撞風險進行了計算分析。
2 碰撞風險模型建立
假設兩架航空器在同一高度飛行,不妨設兩架飛機初始水平間隔為D1,飛機在接下來的ΔT(ΔT很小,趨近于0)時間內,由于飛機的CNS性能環境造成兩架飛機出現一定的定位誤差,假設通信、導航、監視各自的定位誤差是相互獨立的,且根據文獻[9],通信、導航、監視定位誤差導致的偏航往往都服從均值為0的正態分布[10]。
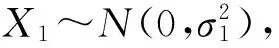
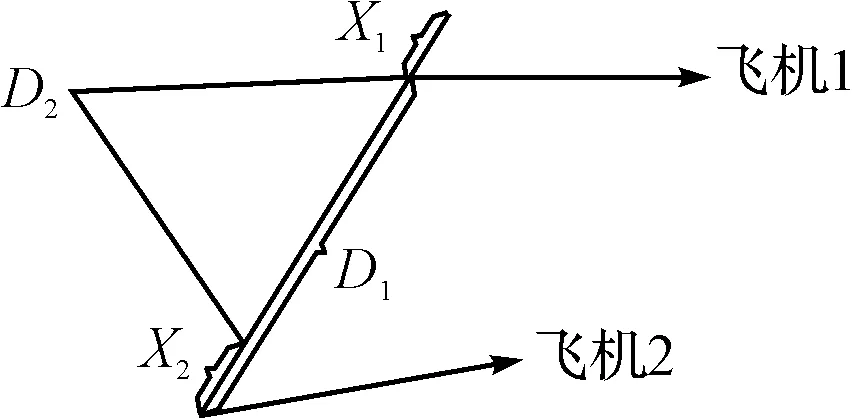
圖1 同高度飛機距離示意圖
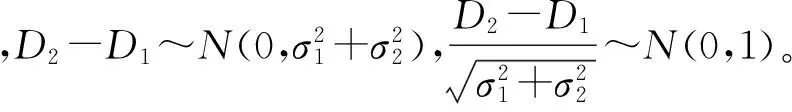
當同一高度層的兩架飛機之間的水平間隔小于飛機尺寸L(L=max(機身長度,翼展長度))時,即認為飛機之間發生了碰撞,因此,兩機碰撞的概率為
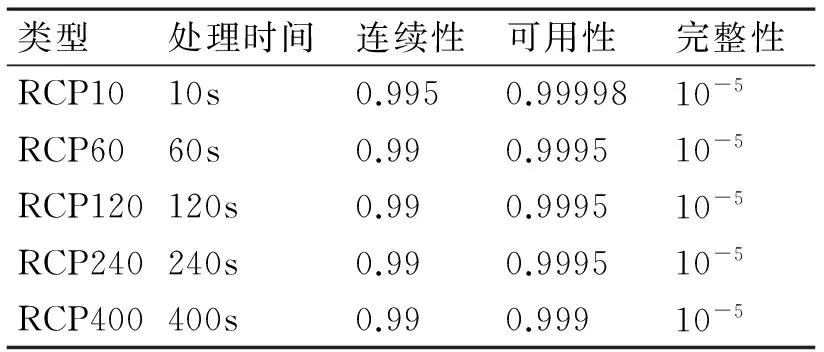
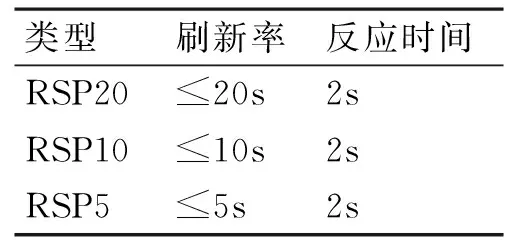
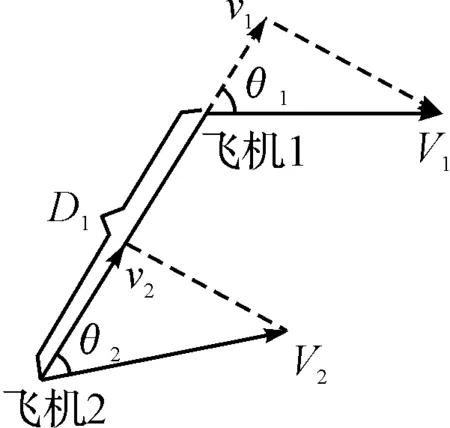
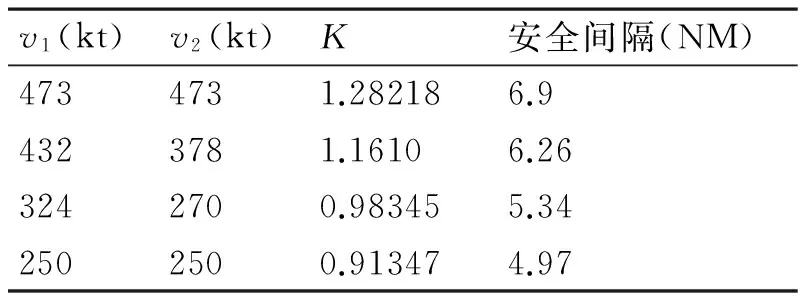
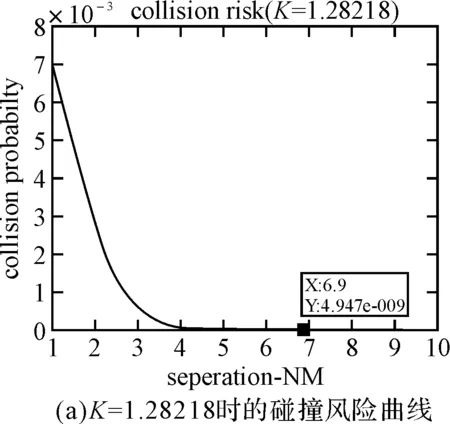
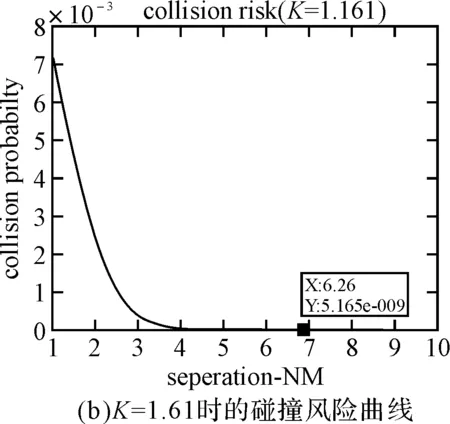
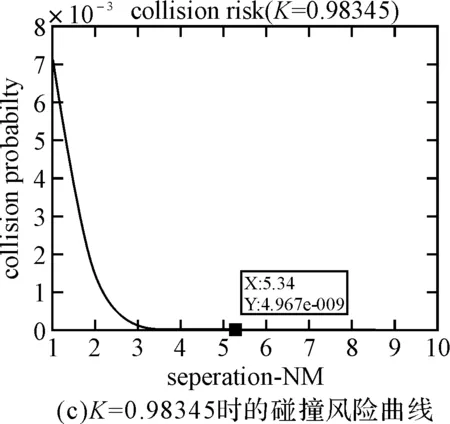
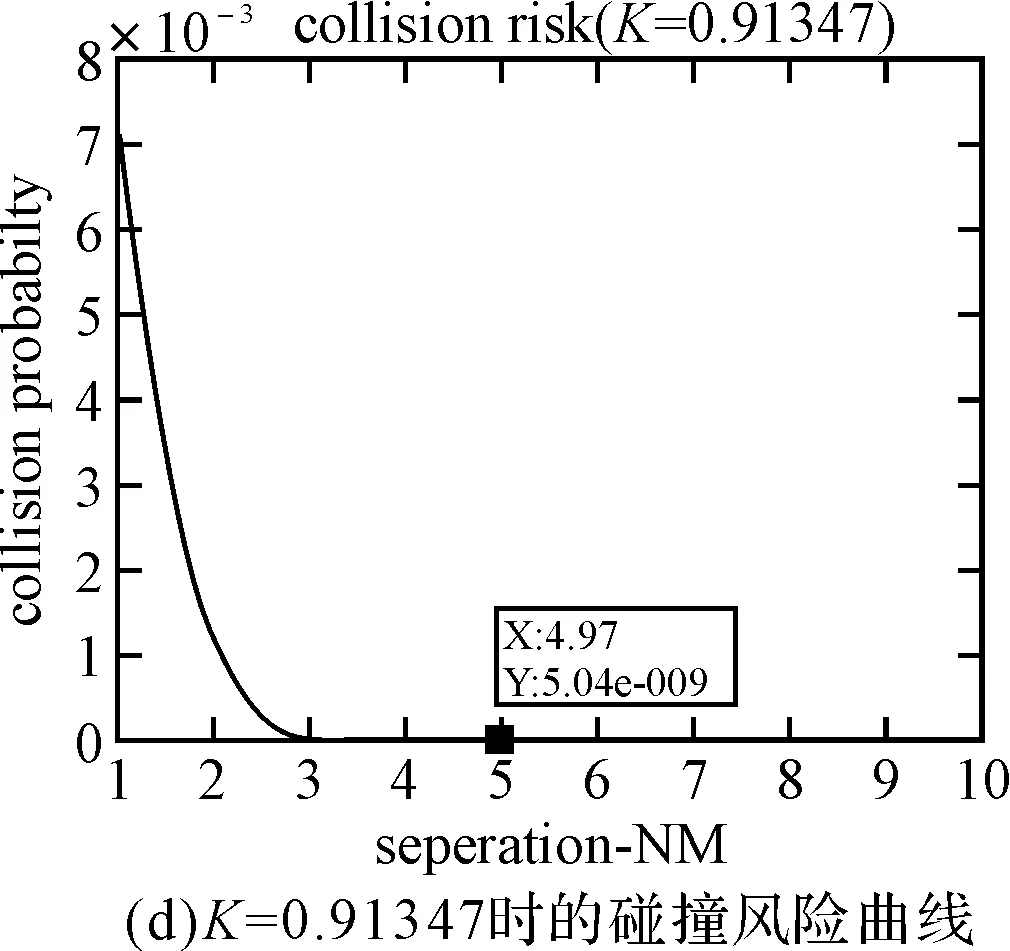
P(|D2| (1) 所以,要想求得碰撞的概率,就需要求解出定位誤差σ(即σ1和σ2),從而需要確定CNS的性能參數。 CNS的性能環境主要分為所需導航性能(RNP)、所需通信性能(RCP)和所需監視性能(RSP)三個方面。 RNP是一種對空域和航路劃分的判據,同時它是對進入該空域或航路飛行的飛機所需導航性能的要求。所需導航性能主要利用導航性能精度劃分空域類型,表1列舉了幾種RNP的類型、參數和應用范圍。 表1 RNP參數表 RCP是通常用處理時間、連續性、可用性和完整性來進行描述,表2給出了它的幾種類型。 表2 RCP參數表 RSP是指在特定的精確度和刷新率條件下,得到航空器的速度、位置的能力,表3列舉了幾種RSP的類型和參數。 表3 RSP參數表 在此,CNS的性能參數分為RNPa、RCPb、RSPc三方面,其中a表示導航精度參數,單位為海里;b表示通信處理時間,單位為秒;c表示監視刷新頻率,單位為秒。根據所需導航性能RNP、所需通信性能RCP和所需監視性能RSP的定義,有如下式子成立: (2) (3) (4) 上述式子中,v是飛機的巡航速度在兩機連線上的分量,σ1、σ2、σ3分別表示導航、通信、監視所導致的水平間隔定位誤差。由式(2)~式(4)可得: 2Φ(a/σ1)-1=0.95 (5) 2Φ(bv/σ2)-1=0.95 (6) 2Φ(cv/σ3)-1=0.95 (7) 從而求得: σ1=a/1.96=0.5102a (8) σ2=bv/1.96=0.5102bv (9) σ3=cv/1.96=0.5102cv (10) 綜上所述,該模型的碰撞概率為 (11) 假設兩架飛機的機型都是B737-200,安全飛行間隔為D1,其翼展長度為28.3m,機身長度為28.6m,所以飛機尺寸L取28.6m,即0.01544海里,兩機飛行速度分別為V1和V2,速度方向與兩機連線的夾角分別為θ1和θ2(圖2)。因此,兩機在連線上的速度分量分別為 v1=V1cosθ1 (12) v2=V2cosθ2 (13) 在此,令 以機載間隔保障系統為例,從機載間隔保障系統的導航性能來看,從美國公布的GPS定位精度已達到米級,所以GNSS已經符合RNP1的要求,所以參數a的取值為1。 供機載間隔保障系統使用的鏈路的傳輸率達到RCP10的要求,所以b的取值為10。 從機載間隔保障系統的監視系統(ADS-B)性能來看,它的更新率達到1s,報文延遲為0.4s~1.2s,所以ASAS符合RSP5的要求,所以c的取值為5。 因此,a=1(海里),b=10(s),c=5(s)。 所以,同高度的碰撞概率公式為 (12) 圖2 兩機速度和間隔示意圖 B737-200的平飛最大速度為473kt(即飛機速度方向與兩機連線的夾角為0時),當θ變化時,兩機連線上的速度v1和v2會減小。結合同高度飛機碰撞模型,通過Matlab軟件對D1從1海里到10海里變化情況下,針對不同的飛行速度進行計算分析(圖3)。由于國際民航組織規定的空中碰撞的安全目標水平為5×10-9,因此可以得到不同K值情況下對應的水平安全間隔(表4)。 表4 不同的飛行速度對應的安全間隔 圖3 不同K值所對應的碰撞風險變化曲線 從圖3可以看出,兩機水平間隔越大,兩機的碰撞概率越小。從表4可以看出,兩機連線上的飛行速度越大(K值越大),所需的最低安全間隔越大。所以在自由飛行的情況下,所需的最小安全間隔應當取K值最大時,所對應的安全間隔。 本文在給定安全目標水平及CNS定位誤差導致的偏航分布下,建立了基于CNS定位誤差的同高度航空器之間的碰撞風險評估模型,由仿真結果該模型及算法具有實際可行性。通過該模型及相應的算法,既可以在給定的安全目標水平及CNS定位誤差下,計算相應的安全間隔,又可以根據安全間隔及CNS定位誤差計算相應的碰撞風險,為以后深入研究CNS性能對碰撞風險的影響提供了一定的理論指導。 [1] REICH P G. Analysis of long-range air traffic systems: separation standards-Ⅰ[J]. Journal of the Institute of Navigation,1966,19(1):88-98. [2] REICH P G. Analysis of long-range air traffic systems: separation standards-Ⅱ[J]. Journal of the Institute of Navigation,1966,19(2):169-186. [3] REICH P G. Analysis of long-range air traffic systems: separation standards-Ⅲ[J]. Journal of the Institute of Navigation,1966,19(3):331-347. [4] Peter Brooker. Longitudinal collision risk for ATC track systems: a hazardous event model[J]. Journal of Navigation,2006,59(1):55-70. [5] Peter Brooker. Lateral collision risk in air traffic systems: a post-reich event model[J]. Journal of Navigation,2003,56(3):399-409. [6] 張兆寧,沈金煒,劉計民.基于CNS定位誤差的側向碰撞風險模型[J].交通運輸工程學報,2009,9(6):110-113. [7] 沈金煒,張兆寧,劉計民.基于CNS定位誤差的平行航路間隔安全評估[J].航空計算技術,2010,40(1):34-36. [8] 張兆寧,劉計民.基于CNS性能的垂直間隔碰撞風險評估[J].中國民航大學學報,2010,28(1):5-8. [9] DAVID E. STEPNER. Modeling of aircraft position errors with independent surveillance[J]. AIAA Journal,1973,11(9):1273-1279. [10] 王欣.空中交通中安全間隔問題的初步研究[D].南京:南京航空航天大學,2001. Flight Separation Safety Assessment Based on CNS Performance HE Wenhong (No. 19 Central Xisanhuan Road, Beijing 100071) In order to ensure the safety separation between the aircrafts under the free flight effectively, the safety flight problems based on the communications, navigation and surveillance performance is studied in this paper. The required communication performance, the required navigation performance and required monitoring performance are analyzed respectively, then the aircraft collision risk model is established combined with probability theory, and the collision risk is calculated and analyzed under the different circumstances of flight speed and flight separation. The analyzed result shows that as the horizontal separation of two aircrafts increases, the collision probability of two aircrafts is smaller. As the velocity component of two aircrafts attachment is greater, the required minimum safety separation is bigger. air traffic management, CNS performance, flight separation, collision risk 2014年11月5日, 2014年12月27日 賀文紅,男,高級工程師,研究方向:指控系統。 V321 10.3969/j.issn1672-9730.2015.05.0093 CNS參數確定

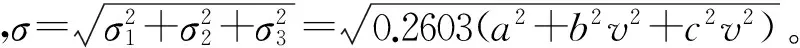
4 實例分析
5 結語

