基于微粒群算法的艦艇計劃修理資源調度優化*

劉 磊 王 平

(海軍工程大學管理工程系 武漢 430033)

?

基于微粒群算法的艦艇計劃修理資源調度優化*

劉 磊 王 平

(海軍工程大學管理工程系 武漢 430033)

為解決艦艇修理計劃中時間和資源制約帶來的問題,提出了基于微粒群算法的艦艇計劃修理資源調度優化方法。將不確定性多項式的求解問題轉化為優先級搜索問題,并利用微粒群算法實現了問題的快速有效求解。工程實例的求解得到了合理有效的分配方案,解決了在資源制約下最小化工期的問題。

微粒群算法; 計劃修理; 資源調度; 優先級

Class Number U674.7

1 引言

艦艇的修理受到時間和資源兩方面的制約。當前艦艇計劃修理中,由于承修單位同時承修多個項目,因而對于單個修理項目,其修理所配備的人力、物力等資源都是有限的。繼而提出了在以縮短修理工期為前提的計劃修理中如何優化調度有限資源的問題[1]。

計劃修理資源調度優化是一個不確定性多項式求解問題,在工程管理方面現行的主要方法是關鍵路徑法,但是該方法以時間最短為前提,無法滿足資源條件的約束,容易出現資源超負荷的問題。

2 艦艇計劃修理進度安排優化模型

一個艦艇修理工程由多個有序的修理項目構成,每個修理項目都有明確的工期要求以及資源需求。修理進度安排優化的目標是充分利用有限的資源,在盡可能短的工期內完成項目,每個項目進行過程中不能中斷,尋優解為各個項目開始與結束的時間。

2.1 艦艇維修工程網絡計劃圖

特定的艦艇修理工程中,各修理項目之間具有前后約束關系,即各修理項目有固定的開工先后順序,將某修理項目之前需要完成的修理項目集合稱為該項目的緊前修理項目,反之為緊后修理項目。通常,用網絡計劃圖表達各維修項目之間的前后約束。

工程網絡計劃圖的實質是有向無環圖(Directed Acyclic Graph,DAG),可以用鄰接矩陣表示。如圖1所示,圖1(a)為一個工程網絡計劃圖,{x1,x2,…,x6}該維修工程所包含的六個維修項目。每個項目對應節點的父節點即為其緊前項目,子節點即為其緊后項目。為了統一工程開始和結束的時間,x1和x6為虛項目,所需工時為0。

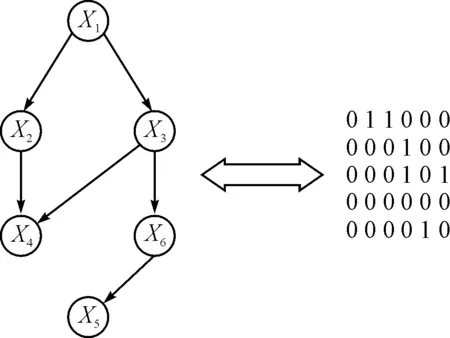
圖1 工程網絡計劃圖及其鄰接矩陣

2.2 艦艇計劃修理進度安排數學模型

艦艇計劃修理進度優化的目標是縮短工期,約束條件包括三項: 1) 修理項目順序制約; 2) 各個修理項目的固定工期; 3) 各種資源限制。其數學模型可表達如下[2]:

mintN
s.t.ti-tj≥dj, ?j∈Zi,i=1,2,…,N

(1)

(2)

其中,N為維修工程包含的項目總數,tN為維修工程的總工期。ti和tj為項目i和項目j的開始時間,di為維修項目i所需要的工期,Zi為項目i的緊前修理項目,m為維修需要的資源種類,rik為修理項目所需要第k類資源的數量,bk為維修工程所配備的第k類資源總量。

上述優化模型中,s.t.(1)隱含約束ti-tj≥0對應于前文的約束條件(1)和(2),表示緊后維修項目必須在緊前維修項目完成的前提下進行,并且項目工期必須足夠。s.t.(2)對應于約束條件(3)為資源約束。

2.3 優化模型的轉換

2.2節描述的數學模型是一個不確定性多項式(NP)問題,需要借助搜索算法尋找問題的解。對于特定的工程網絡計劃圖,其網絡結構確定,節點權值(項目完成時間)確定,因此可以轉化為節點排序的次優求解問題。即將問題的求解轉化為尋找一種項目的優先排序(優先級越高的項目,在資源足夠的條件下,越先進行),使得在該順序之下,維修工程的總計劃工期最短。

由于每個項目的工期固定,為滿足s.t.(1),只需保證緊前項目的優先級大于緊后項目,且緊前項目工期足夠。由于工期所需資源固定,可將s.t.(2)轉化為固定資源的分配,即一旦資源不足,優先級低的維修項目便需要等待前期項目完成再進行資源分配。

3 基于微粒群算法的優化搜索

微粒群算法(Particle Swarm Optimization,PSO)是由美國心理學家Kennedy和電氣工程師Eberhart于1995年提出的一種模擬鳥類群體覓食行為的仿生智能計算方法[3～4]。PSO模型簡單、易于實現、無需梯度信息并在各種連續型優化問題中表現出良好求解效果[5～8]。

微粒群算法的基本思想是通過群體中個體之間的協作和信息共享來尋找最優解。微粒群算法將每個個體看作是在n為搜索空間中的一個沒有重量和體積的微粒,并在搜索空間中以一定的速度飛行,該飛行速度由個體的飛行經驗和群體的飛行經驗進行動態調整[9～10]。

3.1 PSO的搜索方案

(3)

設群體中微粒數為s,群體中所有微粒所經歷過的最好位置為B(t),B(t)∈{P0(t),P1(t),…,Ps(t)},

T(B(t))=min{T(G1(t)),T(G2(t)),…,T(Gs(t))}

(4)

微粒群算法的進化方程可描述為

(5)

式中,下標“i”表示微粒的第i維,即第i個項目的優先級;“k”表示微粒k;t表示第t代;c1、c2為加速常數;為兩個相互獨立的隨機函數。

3.2 目標函數的計算

維修工程需要的總工期是模型的優化目標,對于一個優化方案P,其工程的總工期T(P)的計算方法如圖2所示。具體步驟如下:

Step1 初始化項目調度表,令T(P)=0,調度項目Xj指向虛項目X1。

Step2 查詢調度項目Xj的緊后項目Sj。

Step3 查詢Sj中優先級最高的項目。若該項目已調度過,轉入Step2,否則轉入Step4。

Step4 查詢項目的緊前項目,若完成,轉入Step5,否則轉入Step3。

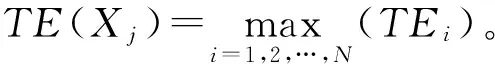
Step6 判斷項目是否全部調度完畢,若未完成,存儲已調度項目序號,并令j=j+1,轉入Step2,否則,轉入Step7。

Step7 令T(P)=TE(Xj)。

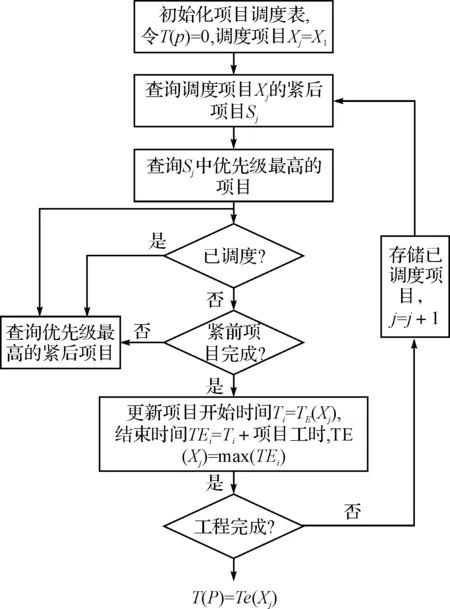
圖2 總工期計算流程

4 實例

選取某艦艇維修工程實例部分計劃進行優化分析。該工程所需人力資源包括電工、鉗工和銅工三種,每天可調度人數分別為30、10、20。圖3為該維修計劃的工程網絡計劃圖,表1為各個項目所需工期和資源。

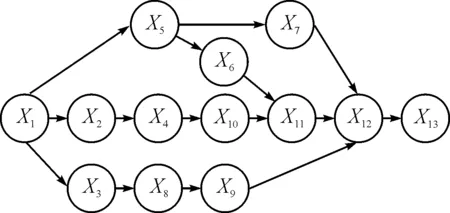
圖3 工程網絡計劃圖

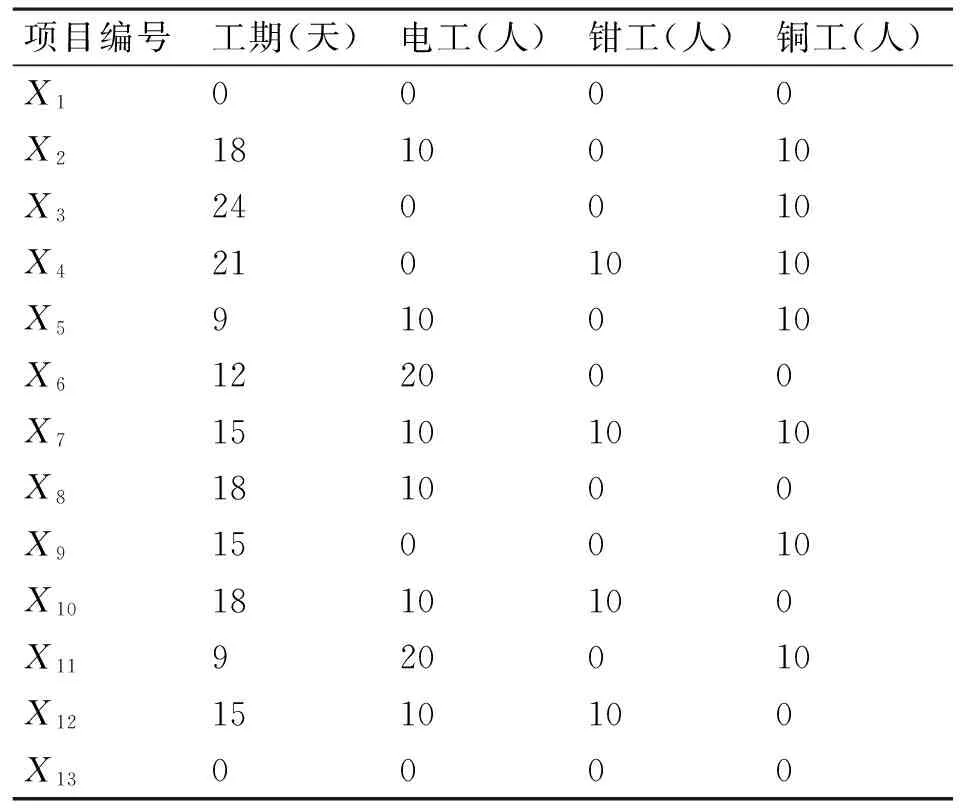
項目編號工期(天)電工(人)鉗工(人)銅工(人)X10000X21810010X3240010X42101010X5910010X6122000X715101010X8181000X9150010X101810100X11920010X121510100X130000

為了滿足微粒群體搜索范圍的有效性,設定群體規模s為10,加速常數c1、c2均為0.5,采用Matlab2009R編程,Win7操縱環境,搜索結束條件為運行100代(t=100),或最優目標值保持不變10代。

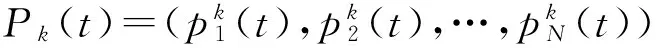
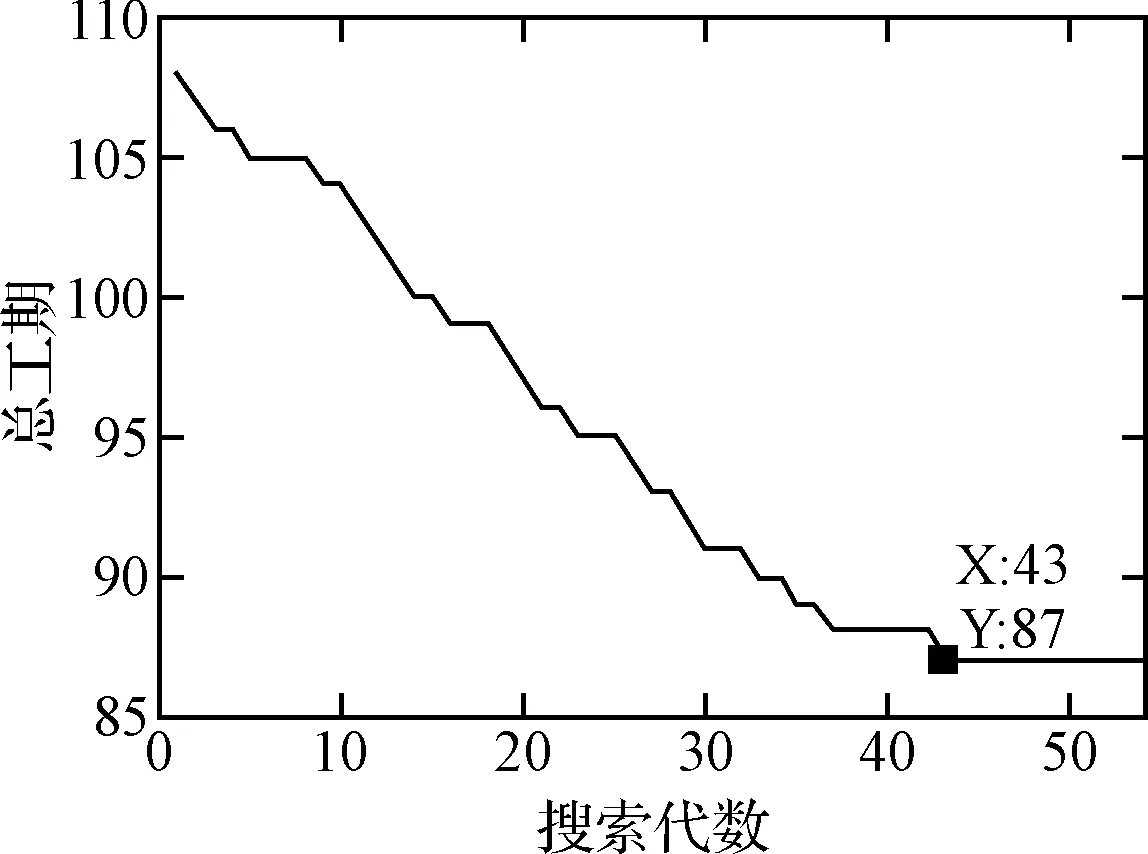
圖4 優化搜索過程

圖4為優化搜索的過程,如圖所示,隨著搜索代數的增加,維修工程的總工期(圖中取值為所有微粒最好位置時的工期)逐漸縮短,優化呈現收斂態勢。在第44代時到達最優維修工期87天,最優值保持10代到達54代時搜索停止。

根據總工期計算流程,可以得到修理工程計劃調度如表2所示。

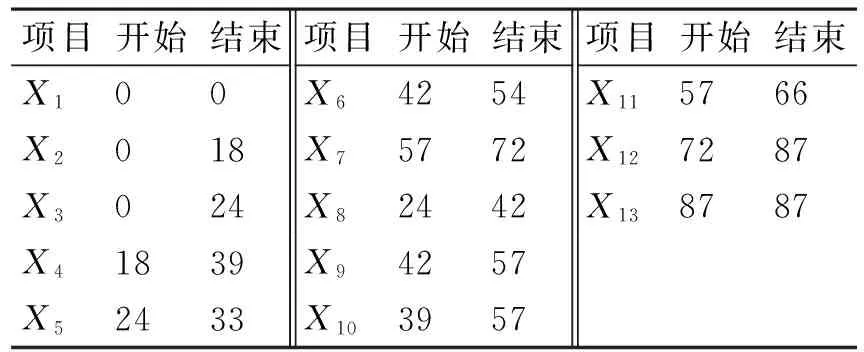
表2 修理工程計劃調度表

5 結語

解決資源受限的計劃維修項目調度問題,其難點是NP問題的尋優求解。本文將NP問題轉化為優先級的尋優搜索,利用PSO算法求得調度方案。所研究方法具有一定的工程實用價值。

[1] 高健.船舶修理管理研究及信息系統開發[D].上海:上海海事大學,2007.

[2] 周世雷,鄭映烽,劉子楊,等.艦艇計劃修理資源約束性項目調度優化[J].四川兵工學報,2013,34(8):86-89.

[3] Kennedy J, Eberhart R C. Particle swarm optimization[C]//Proceeding of 1995 IEEE International Conference on Neural Networks. New York, NY, USA: IEEE,1995:1942-1948.

[4] 謝曉鋒,張文俊,楊之廉.微粒群算法綜述[J].控制與決策,2003,18(2):129-134.

[5] 沙立成,宋珺琤.基于改進粒子群優化LS-SVM的變壓器故障氣體預測[J].華北電力大學學報,2011,38(1):35-38.

[6] 朱童,李小凡,魯明文.位置加權的改進粒子群算法[J].計算機工程與應用,2011,47(5):4-6.

[7] 趙志剛,常成.帶變異算子的自適應粒子群優化算法[J].計算機工程與應用,2011,47(17):42-44.

[8] 任子暉,王堅.加速收斂的粒子群優化算法[J].控制與決策,2011,26(2):201-206.

[9] 梁昔明,董淑華.動態慣性權重和維變異的粒子群優化算法[J].計算機工程與應用,2011,47(5):29-31.

[10] 高浩,冷文浩,須文波.一種全局收斂的PSO算法及收斂分析[J].控制欲決策,2009,24(2):196-201.

Optimization of Resource-Constrained Ship Project Scheduling Based on PSO

LIU Lei WANG Ping

(Department of Management Engineering, Naval University of Engineering, Wuhan 430033)

To solve the problem caused by the time and resource constraints in the ship scheduled repair, the particle swarm optimization algorithm for resource scheduling is put forward. The problem of solving polynomial uncertainty is converted into priority search problem, and then the particle swarm algorithm is used to achieve a rapid and effective solving. The engineering examples has been solved reasonably and effectively, solving the problem of minimal with the chemicals resource constraints.

particle swarm optimization, scheduled repair, resource scheduling, priority

2014年11月19日,

2014年12月30日

劉磊,男,碩士研究生,研究方向:軍事運籌、裝備保障。王平,男,教授,碩士生導師,研究方向:指揮等。

U674.7

10.3969/j.issn1672-9730.2015.05.029