基于Autocad地形圖坐標轉換系統研究

王　義

(中鐵二院工程集團有限責任公司，四川成都　610031)

Research on Autocad Based on Topographic Map Coordinate System Conversion

WANG Yi

基于Autocad地形圖坐標轉換系統研究

王義

(中鐵二院工程集團有限責任公司，四川成都610031)

Research on Autocad Based on Topographic Map Coordinate System Conversion

WANG Yi

摘要介紹同橢球和不同橢球的地形圖坐標轉換方法，并基于Autocad平臺，利用ObjectARX工具開發(fā)地形圖坐標轉換系統，應用于多個高鐵項目，取得了較好的效果。

關鍵詞高斯投影四參數七參數ObjectARX坐標轉換

1概述

隨著我國高鐵技術的迅速發(fā)展，鐵路勘察設計標準更加規(guī)范，對鐵路設計各環(huán)節(jié)的精度要求不斷提高。為了減少長距離鐵路全線制圖帶來的投影變形誤差，鐵路勘察設計中必須針對鐵路全線進行多個投影分帶，以便更好的控制投影變形，提高鐵路勘察設計精度。伴隨投影分帶的不斷細化，帶來了大量的地形圖坐標轉換工作。

詳細介紹兩種地形圖坐標轉換方法，一是同橢球下高斯投影正反算坐標換帶法，二是不同坐標系下通過公共點解算四參數、七參數轉換法。在此基礎上，首次將高斯投影正反算、四參數、七參數公式引入AutoCAD平臺，利用ObjectARX工具開發(fā)了地形圖坐標轉換軟件，保證了換帶精度，提高了作業(yè)效率。

2數字地形圖坐標轉換方法

常用的地形圖坐標轉換方法有兩種，同橢球高斯投影正反算法及不同橢球四參數、七參數轉換法。

2.1　同橢球高斯投影正反算法

為了限制長度變形，以中央子午線進行分帶，把投影范圍限制在中央子午線東、西兩側一定的范圍內，使得統一的坐標系分割成各帶的獨立坐標系。在工程應用中，往往要用到相鄰帶中的點坐標，這樣便涉及到換帶計算。

地形圖轉換前后的坐標系如果是基于同橢球的，并且投影方式相同，可直接采用投影換帶計算，投影方式較常用的有高斯投影、UTM投影及蘭勃特投影等。高斯投影正算公式為

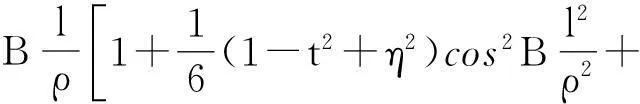
(1)

高斯投影反算公式為

(2)

式中ηf、tf分別為按Bf值計算的相應量。

a為橢球長半軸，帶高程抵償面時：長半軸=長半軸理論值+高程抵償面高程值。為消除長度變形誤差，通常做法是選擇合適的基準投影面以使綜合變形在容許變形范圍之內，這個基準投影面我們稱之為抵償高程面。

b為橢球短半軸，f為橢球扁率，X為子午線弧長，Bf為底點緯度，帶有高程抵償面的解算，在具有高程抵償面進行高斯變換時，應該將緯度B的差值代入

ΔB=sin2B(1-e2sin2B)Z0f/((a+Z0)(1-e2))，

式中，Z0為高程抵償面的高程。

2.2　不同橢球四參數、七參數轉換法

地形圖轉換前后的坐標系如果是基于不同的橢球，需要利用公共點在兩個坐標系下不同的坐標值計算四參數、七參數，通過這些參數計算每個實體轉換后的坐標，修改實體坐標為轉換后坐標，完成不同橢球下地形圖的轉換工作。

四參數轉換法公式為

(3)

式(3)中，x2，y2為轉換后的平面直角坐標，x1，y1為原坐標系下平面直角坐標，坐標單位為m。x0，y0為平移參數，α為旋轉參數，m為尺度參數。解算這4個參數，需要兩個以上公共點。

七參數轉換法公式為

(4)

3地形圖坐標轉轉換系統的設計與實現

為了提高坐標轉換自動化程度，同時減少人工轉換可能出現的差錯，根據實際情況，引用不同的轉換模型，利用ObjectARX工具，采用點對點轉換方法，即遍歷整個AutoCAD文件中的實體，對單個實體定位點坐標進行轉換計算，然后修改單個實體定位點的坐標為變換后的坐標，開發(fā)了數字地形圖坐標轉換軟件。該軟件基于AutoCAD平臺底層開發(fā)，程序運行穩(wěn)定，轉換速度快，可實現海量數據批量轉換。

基于相同橢球轉換時，可查閱1954北京橢球、1980西安橢球、WGS84橢球、國家2000橢球等通用橢球，或自定義橢球的長、短半軸，橢球扁率參數，代入公式(1)、(2)，可實現任意中央子午線、任意高程抵償面間的高精度轉換。數字地形圖坐標轉換軟件能實現自動轉換，開發(fā)環(huán)境采用ObjectARX2008與VS2005，同橢球坐標轉換流程如圖1所示。

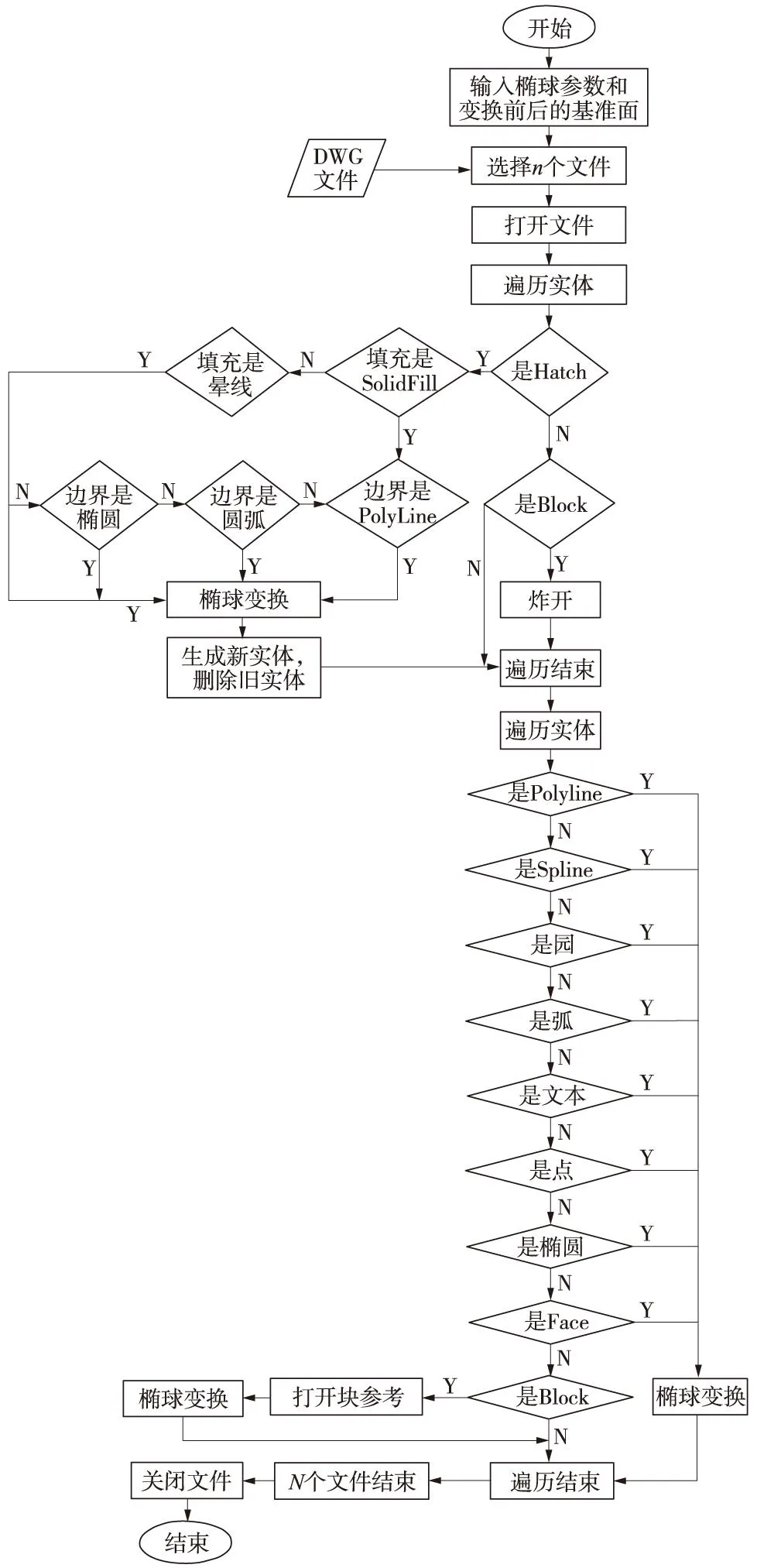
圖1　同橢球坐標轉換流程

基于不同橢球或者任意坐標系的轉換，四、七參數轉換法都可以實現，但考慮地形圖轉換要保證高程值不改變，四參數轉換法更具有實際意義，帶有高程的坐標文本文件轉換可采用七參數轉換法。四參數轉換流程如圖2所示。

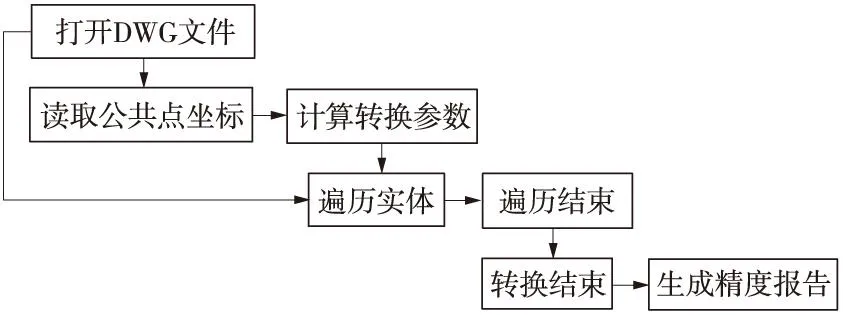
圖2　四參數坐標轉換流程

程序同時提供轉換精度報告，即每個公共點的改正量，改正量如異常，檢查公共點輸入格式及判斷粗差點，剔除粗差點，再進行參數計算，完成地形圖坐標系轉換。

對圖形文件進行轉換時，根據實體類型的不同，做出相應的轉化。例如，針對圖案填充實體可轉換其邊界，刪除原有圖案填充，依據新邊界重新填充圖案；坐標范圍較大的塊(Block)及嵌套塊，如果直接轉換誤差會比較大，對于這種塊程序采取打散后轉換；文字注記、高程點及植被符號以插入點坐標進行轉換；圓弧曲線轉換起始點、終止點及中心點坐標，然后重新生成圓弧曲線；標注實體按標注線和標注文本分開轉換；通過以上手段解決了難以轉換的實體，保證換帶無遺漏。

在實際項目中，會同時涉及到同橢球和不同橢球的轉換，為了保證轉換精度，經常綜合運用高斯正反算法及四參數法。

下面以一個實例來闡述地形圖換帶流程。某項目地形圖為北京54橢球，中央子午線經度100.5°，高程抵償面大地高1 020 m；轉換到WGS84橢球，中央子午線經度101.75°，高程抵償面大地高為1 060 m。可先利用高斯反算模塊將地形圖及公共點轉換到相同中央子午線，再利用四參數模塊進行轉換，這樣，公共點投影到相同中央子午線，四參數轉換殘差最小，精度最高。最后在同橢球下，利用高斯正算模塊將地形圖轉換到對應的工程獨立坐標系。圖3為詳細的換帶流程。

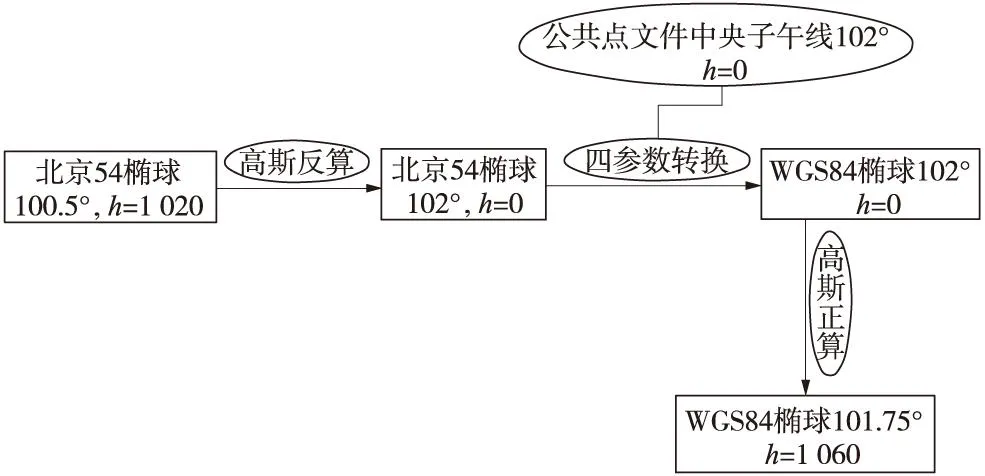
圖3　地形圖換帶流程

4轉換精度檢核

4.1　同橢球換帶精度檢查

隨機抽取某幅地形圖內26個實體坐標，轉換前坐標系采用WGS84橢球，中央子午線經度為103.25°，高程抵償面大地高為1940 m；轉換后坐標系采用WGS84橢球，中央子午線經度為106.5°，高程抵償面大地高為1 255 m。通過本軟件計算和西南交大的GPS2005軟件計算，比較計算結果，其差值如表1。

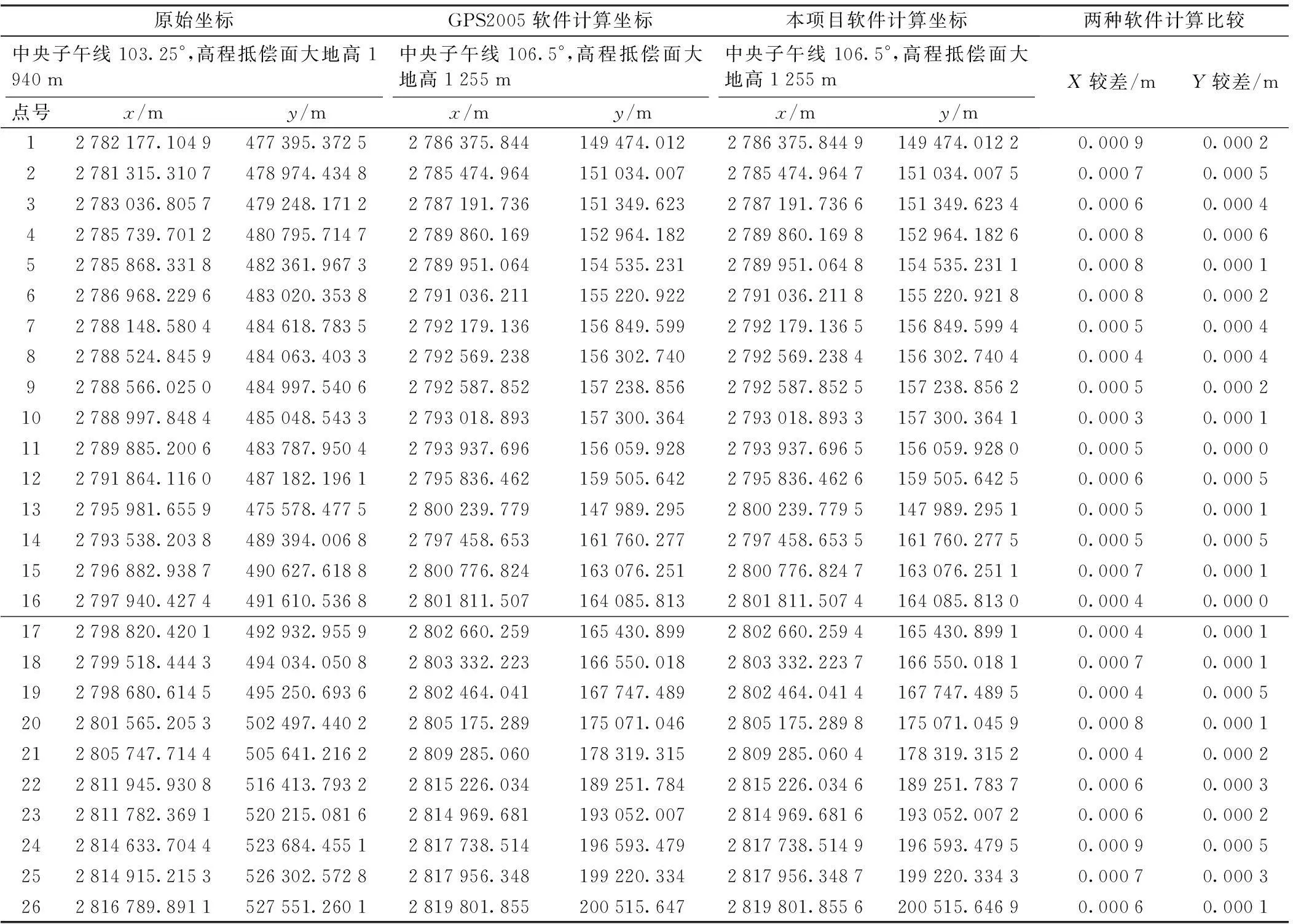
表1　同橢球換帶殘差比較

4.2　參數換帶精度檢查

實驗數據為機載Lidar點云數據，原始坐標系采用Clarke 1880(克拉克)橢球，中央子午線39°，高程抵償面大地高為0 m，投影方式為UTM投影；換帶后的坐標系采用WGS84橢球，中央子午線39°，高程抵償面大地高為0 m，投影方式為高斯投影；經分析前后坐標系為不同橢球，只能利用公共點進行轉換，通過本軟件選擇四參數法計算和Cosawin(科傻)軟件選擇赫爾默特法計算，比較計算結果，其差值如表2。

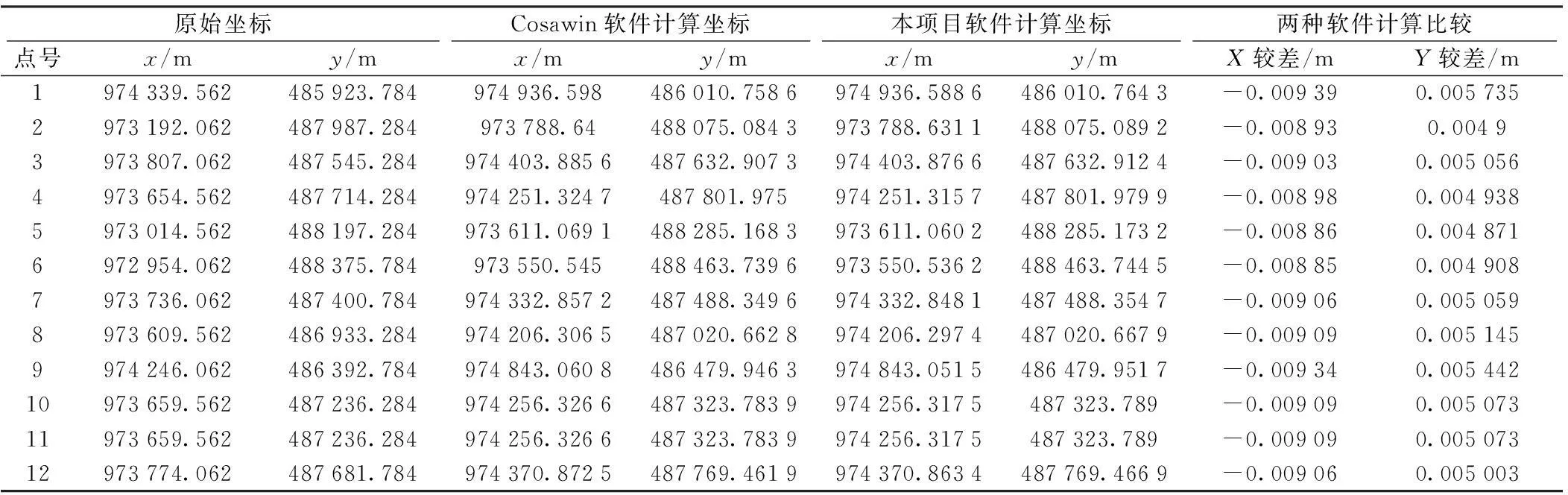
表2　參數換帶殘差比較

從表2統計可見，同橢球高斯正反算轉換法精度優(yōu)于0.1 mm，不同橢球參數轉換法精度可控，與公共點精度相關。

通過多個項目驗證得知，高斯投影正反算法，轉換公式嚴密，換帶精度較高。精度不受長距離、中央子午線經度跨度較大的影響。四參數、七參數轉換方法，通過公共點計算平移、旋轉以及縮放參數，近似實現兩個坐標系的轉換。該方法對于短距離、中央子午線經度跨度不大的情況，轉換方法嚴密有效。但對于長距離、中央子午線經度跨度較大時，轉換精度較差。

5結論

為了解決海量數字地形圖基于多個投影分帶的換帶問題，探索將大地測量學數學模型引入AutoCAD平臺，結合ObjectARX工具開發(fā)的地形圖轉換軟件，實現了高精度、無遺漏及快速批量轉換數字地形圖功能，經過多個高鐵項目實踐驗證，轉換精度可靠，具有較強的實用性。

參考文獻

[1]周適.七參數坐標轉換研究及應用[J].鐵道勘察，2013(5)

[2]楊鋒，林春峰，程昂.基于ObjectArx地形圖數據標準統一軟件的設計與實現[J].鐵道勘察，2014(5)

[3]梅熙.高速鐵路坐標轉換方法探討[J].高速鐵路技術，2012(8)

[4]管建華.基于ObjectARX的空間數據坐標變換及應用[J].現代測繪，2007(1)

[5]鄭敏輝,林鐵.數字地形圖坐標轉換工具的設計與實現[J].測繪技術裝備，2008(1)

[6]劉秀軍,孫小英,袁月欣.省區(qū)矢量數字地圖WGS-84坐標系與1980西安坐標系的轉換[J].測繪，2011(6)

[7]孔祥元,郭際明,劉宗泉.大地測量學基礎[M].武漢：武漢大學出版社，2001

[8]呂忠剛,許世寧.關于抵償高程面與移動中央子午線最佳選取問題的研究[J].東北測繪，2002(2)

[9]王小華,程傳錄,范宏濤，等.基于AutoCAD.NET API的地形圖坐標轉換實現方法研究[J].測繪與空間地理信息，2013(11)

[10]楊本廷.數字地形圖坐標變換的探討[J].城市勘測，2010(1)

中圖分類號：P284

文獻標識碼：B

文章編號：1672-7479(2015)02-0001-04

作者簡介：王義(1975—)，男，2000年畢業(yè)于武漢測繪科技大學攝影測量與遙感專業(yè)，工學學士，高級工程師。

收稿日期：2014-12-31