一類不連續(xù)映射的邊界碰撞分岔分析
諸葛得莉,李群宏
(廣西大學(xué) 數(shù)學(xué)與信息科學(xué)學(xué)院,南寧530004)
?
一類不連續(xù)映射的邊界碰撞分岔分析
諸葛得莉,李群宏
(廣西大學(xué) 數(shù)學(xué)與信息科學(xué)學(xué)院,南寧530004)
本文討論一類分段非線性的不連續(xù)映射.首先通過數(shù)值仿真得到單參數(shù)的分岔圖,發(fā)現(xiàn)該映射存在加周期序列和周期疊加序列.其次,分析了一個典型的周期n+1解及迭代表達(dá)式;并推導(dǎo)了映射RLn序列周期n+1解的邊界碰撞分岔?xiàng)l件,通過數(shù)值仿真得到平面上RLn的周期區(qū)域全局分岔圖.從而,我們驗(yàn)證該映射由于周期n+1解的邊界碰撞分岔形成了加周期序列和周期疊加序列.
不連續(xù)映射;周期n+1解;邊界碰撞分岔;加周期序列;周期疊加序列
0 引言
由于不連續(xù)系統(tǒng)在社會科學(xué)和自然科學(xué)領(lǐng)域中廣泛的存在性,在過去幾年,非光滑系統(tǒng)的分岔及其動力學(xué)行為吸引了越來越多學(xué)者的關(guān)注,特別是系統(tǒng)參數(shù)變化時導(dǎo)致周期解碰撞引起的邊界碰撞分岔現(xiàn)象.如文獻(xiàn)[1]針對一個二維的分段映射,最早給出了邊界碰撞分岔的定義.文獻(xiàn)[2]針對二維分段光滑映射,研究了邊界碰撞分岔的六種類型以及不同分岔出現(xiàn)的動力學(xué)行為.對于n維分段映射中的邊界碰撞分岔,文獻(xiàn)[3]將邊界碰撞分岔成果進(jìn)行了分類.文獻(xiàn)[4]針對一個一維的連續(xù)型線性-曲線映射,分析其周期環(huán)的倍周期分岔?xiàng)l件,并推導(dǎo)邊界碰撞分岔可能出現(xiàn)的動力學(xué)行為.文獻(xiàn)[5]給出了一維及兩維分段光滑連續(xù)映射的邊界碰撞分岔?xiàng)l件,并研究邊界碰撞分岔與非退化分岔之間的關(guān)系.文獻(xiàn)[6]研究一維連續(xù)型的分段光滑非線性映射(平方根映射),給出了邊界碰撞分岔曲線及鞍結(jié)分岔曲線的存在區(qū)域.文獻(xiàn)[7-10]針對分段光滑不連續(xù)映射,推導(dǎo)了邊界碰撞分岔?xiàng)l件,發(fā)現(xiàn)該系統(tǒng)能產(chǎn)生加周期、周期疊加、極限環(huán)、混沌等復(fù)雜的動力學(xué)行為.文獻(xiàn)[11]分析了低周期的邊界碰撞分岔,數(shù)值仿真得到周期疊加序列的存在性.文獻(xiàn)[12]對于一維的具有兩個不連續(xù)點(diǎn)的分段線性映射,得出當(dāng)參數(shù)變化時邊界碰撞分岔能形成加周期序列和周期疊加序列.文獻(xiàn)[13-14]針對一個線性-曲線型不連續(xù)映射,研究其邊界碰撞分岔,推導(dǎo)了周期解的邊界碰撞分岔?xiàng)l件,得到周期環(huán)的存在區(qū)域及兩個環(huán)的共存域.文獻(xiàn)[15]針對一維分段線性不連續(xù)映射,研究其邊界碰撞曲線出現(xiàn)的動力學(xué)行為,發(fā)現(xiàn)會出現(xiàn)增量為一或多于一的周期疊加及多次疊加這類周期的存在區(qū)域.
文獻(xiàn)[16]研究的模型是連續(xù)型分段映射
(1)

1 數(shù)學(xué)模型
本文討論的模型為不連續(xù)分段映射,即
(2)
其中0
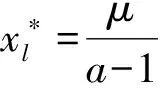
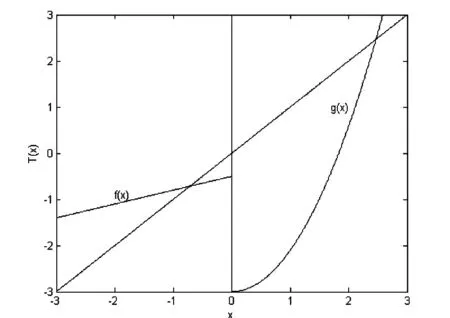
圖1 a=0.9 ,b=0.9,l=-2.5,μ=-0.5系統(tǒng)(2)的圖像
1.1 系統(tǒng)(2)以μ為分岔參數(shù)的分岔圖像
給定參數(shù)a=0.9,b=0.9,l=2.5,數(shù)值仿真得到系統(tǒng)(2)關(guān)于參數(shù)μ的分岔圖像,如圖2所示.可以看到系統(tǒng)(2)存在加周期序列和周期疊加序列.在μ(0,1.2),隨著參數(shù)μ的減少,周期2經(jīng)過周期疊加序列變?yōu)橹芷?序列;再經(jīng)過周期疊加序列變?yōu)橹芷?序列,依此類推.同時發(fā)現(xiàn)在μ(0.4,0.6),周期4和周期5之和剛好等于其間的周期9這類現(xiàn)象.在μ(1.2,1.3),隨著參數(shù)μ的減少,周期9以公差為2成遞增的等差數(shù)列依此遞增,直到出現(xiàn)混沌.
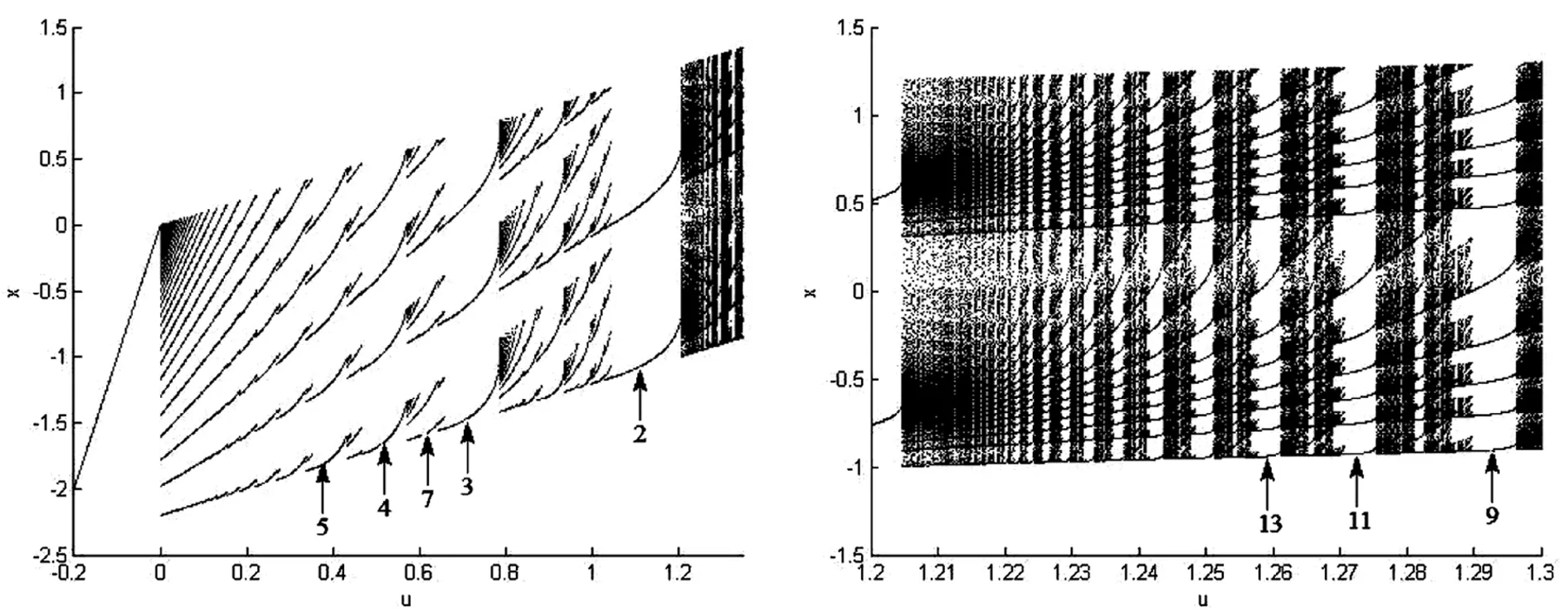
圖2 a=0.9,b=0.9,l=-2.5(a)系統(tǒng)(2)關(guān)于μ的分岔圖像, (b)局部放大圖
1.2 系統(tǒng)(2)的RLn序列的邊界碰撞分岔分析
一個典型的周期n+1解(n≥1)定義為{x0
(3)
由上式得到迭代點(diǎn)xn的表達(dá)式為

(4)
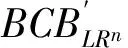
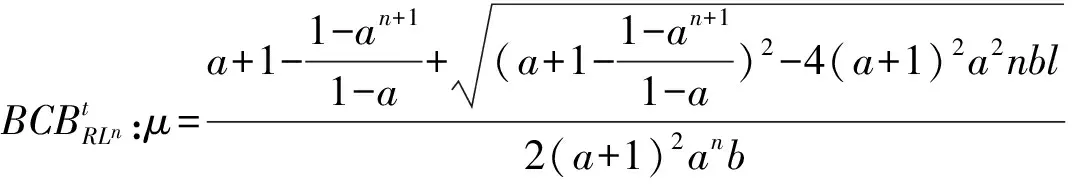
(5)
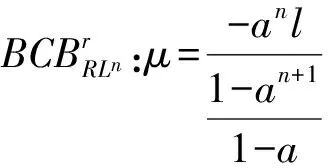
(6)

圖3 b=0.9,l=-2.5時平面(a,μ)上的LRn周期存在區(qū)域
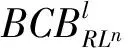
2 結(jié)論
本文針對左邊為線性函數(shù)右邊為非線性函數(shù)的分段不連續(xù)的系統(tǒng)(2)展開研究.首先討論了其發(fā)生邊界碰撞的條件;然后通過數(shù)值仿真驗(yàn)證了這些條件的正確性,從而得到系統(tǒng)(2)確實(shí)存在加周期序列和周期疊加序列.
[1]Nusse H E, Ott E, Yorke J A. Border-collision bifurcations: An explanation for observed bifurcation phenomena[J].Physical Review E, 1994, 49(2): 1073.
[2]Banerjee S, Grebogi C. Border collision bifurcations in two-dimensional piecewise smooth maps[J].Physical Review E, 1999, 59(4): 4052.
[3]Di Bernardo M, Feigin M I, Hogan S J, et al. Local analysis of C-bifurcations in n-dimensional piecewise-smooth dynamical systems[J].Chaos Solitons and Fractals, 1999, 10(11): 1881-1908.
[4]Gardini L, Tramontana F, Sushko I. Border collision bifurcations in one-dimensional linear-hyperbolic maps[J].Mathematics and Computers in Simulation, 2010, 81(4): 899-914.
[5]Sushko I, Gardini L. Degenerate bifurcations and border collisions in piecewise smooth 1D and 2D maps[J].International Journal of Bifurcation and Chaos, 2010, 20(7): 2045-2070.
[6]Avrutin V, Dutta P S, Schanz M, et al. Influence of a square-root singularity on the behaviour of piecewise smooth maps[J].Nonlinearity, 2010, 23(2): 445-463.
[7]Jain P, Banerjee S. Border-collision bifurcations in one-dimensional discontinuous maps[J].International Journal of Bifurcation and Chaos, 2003, 13(11): 3341-3351.
[8]Avrutin V, Schanz M, Banerjee S. Multi-parametric bifurcations in a piecewise-linear discontinuous map[J].Nonlinearity, 2006, 19(8): 1875-1906.
[9]Avrutin V, Schanz M. On multi-parametric bifurcations in a scalar piecewise-linear map[J].Nonlinearity, 2006, 19(3): 531-552.
[10]Tramontana F, Gardini L, Agliari A. Endogenous cycles in discontinuous growth models[J].Mathematics and Computers in Simulation, 2011, 81(8): 1625-1639.
[11]Kumar A, Banerjee S, Lathrop D P. Dynamics of a piecewise smooth map with singularity[J].Physics Letters A, 2005, 337(1): 87-92.
[12]Bischi G I, Gardini L, Tramontana F. Bifurcation curves in discontinuous maps[J].Discrete and Continuous Dynamical Systems-Series B, 2010, 13(2): 249-267.
[13]韋麗梅.分段映射的邊界碰撞分岔及混沌控制[D].廣西: 廣西大學(xué), 2013.
[14]Tramontana F, Gardini L. Border collision bifurcations in discontinuous one-dimensional linear-hyperbolic maps[J].Communications in Nonlinear Science and Numerical Simulation, 2011, 16(3): 1414-1423.
[15]Gardini L, Tramontana F. Border collision bifurcation curves and their classification in a family of 1D discontinuous maps[J].Chaos, Solitons and Fractals, 2011, 44(4): 248-259.
[16]秦志英, 李群宏. 一類非光滑映射的邊界碰撞分岔[J].力學(xué)學(xué)報, 2013, 45(1): 25-29.
Border Collision Bifurcation in a Class of Discontinuous Maps
ZHUGE De-li, LI Qun-hong
(School of Mathematics and Information Sciences, Guangxi University, Nanning,530004, China)
A class of discontinuous piecewise nonlinear maps are considered in the current paper. First of all, one-parameter bifurcation diagrams are obtained by numerical simulations. Then it is found that the maps have periodic adding sequences and periodic stacking sequences. Secondly, the typical periodicn+1 solutions and the iterative expressions are analyzed, and periodicn+1solution conditions of border collision bifurcation in theRLnsequences are deduced. Hence, the periodic regional global diagram in theRLnplane is obtained by the numerical simulation. Finally, it is verified that the map has periodic adding sequences and periodic stacking sequences due to border collision bifurcations of periodicn+1 solutions.
discontinuous maps; periodicn+1 solutions; border collision bifurcations; periodic adding series; periodic stacking sequences
2015-05-18
國家自然科學(xué)基金項(xiàng)目(No.11372077)
諸葛得莉(1990-),女,廣西桂林人,廣西大學(xué)數(shù)學(xué)與信息科學(xué)學(xué)院2013級應(yīng)用數(shù)學(xué)專業(yè)碩士研究生,研究方向?yàn)榉蔷€性動力學(xué).
李群宏(1964-),男,廣西南寧人,廣西大學(xué)數(shù)學(xué)與信息科學(xué)學(xué)院教授,研究方向?yàn)槌N⒎址匠潭ㄐ岳碚摵头蔷€性動力學(xué)理論與應(yīng)用.
O189.1
A
1008-6722(2015) 05-0006-04
10.13307/j.issn.1008-6722.2015.05.02

