Dijkstra算法在三亞旅游線路規劃中的應用

王哲河,林 越,張 僑

(瓊州學院 a.計算機工程學院; b.數學系; c.旅游學院,海南 三亞572022)

?

Dijkstra算法在三亞旅游線路規劃中的應用

王哲河a,林 越b,張 僑c

(瓊州學院 a.計算機工程學院; b.數學系; c.旅游學院,海南 三亞572022)

建立數學模型,結合數據庫技術,運用Dijkstra算法,計算出任意兩個景點之間的最低費用、最短時間、最短路程,供游客路線選擇和相關管理者規劃旅游線路時參考.

數據庫;Dijkstra;最短路徑

0 引言

海南國際旅游島建設背景下,三亞因其得天獨厚的地理位置,獨特豐富的旅游資源,成為了國內外旅游者青睞的旅游目的地之一.設計合理的旅游線路,方便游客選擇,降低旅游的資金、時間和精力成本是提高城市旅游管理水平、旅游形象及旅游競爭力的重要途徑.旅游線路的優化設計問題已經成為國內外學術界研究的重要領域.為便于研究,同時不影響模型的適用性和科學性,本文從眾多線路設計影響因素中抽取景點間路程和道路類型兩個關鍵要素,設置相應的權值,構建三亞旅游線路優化設計的數學模型,利用現代數據庫技術和經典Dijkstra算法設計出了最優(路程、時間、費用)旅游線路,可供游客選擇和管理者決策參考.

1 Dijkstra算法的由來

目前,求最短路徑的算法有Dijkstra 算法、Floyd-Warshall算法、Bellman-Ford算法、Johnson算法等,每種算法都有其獨特的優點,其中由荷蘭計算機科學教授E.W.Dijkstra于1959 年率先提出的Dijkstra 算法可謂最經典,它主要用于解決有向圖中源點到其他節點的最短路徑問題[1-3,5].Dijkstra 算法的主要思想是從源點開始查找邊長最短的相鄰點,然后又以此相鄰點作為新源點查找邊長最短的相鄰點,并記錄沿途各個點(若到達新源點各邊長之和大于前面各邊長之和時須退回到上一個源點,換一條各邊長之和次短的相鄰點作為新源點繼續查找),以此類推,直到新的相鄰點為目的點且到達目的點的各邊長之和最短時就停止查找.此外,邊權賦予的含義不同,其最短路徑的含義也不同,如邊權值表示的是交通費時,最短路徑實際指的是最少交通費.

2 三亞旅游線路的數學模型構建

根據Dijkstra 算法主要思想,結合三亞景點的布局情況,可得出影響游客出行的兩個關鍵要素是景點間路程和道路類型,兩者決定交通費用高低和所需時間多少[4-6].為了便于研究,選擇三亞的幾個主要景點及連通各景點的公路所構成的景點圖 (如圖1所示)作為研究對象,并約定:

①景點:用圓圈代表,圓圈內的數據如65|90表示天涯海角景點門票為65元,停留(參觀)時間為90分鐘,V4中的4表示天涯海角的景點號.

②景點間路程:用曲線代表,曲線邊上的數據如45|1,45表示南山寺至落筆洞兩景點的直通路程為45公里,1表示此路為高速公路.

③交通費用計算方法:高速公路1.5元/km、普通公路2元/km.

④圖1中相關數據是以三亞市公交車實際行駛路程為基礎進行處理后抽象的數據.

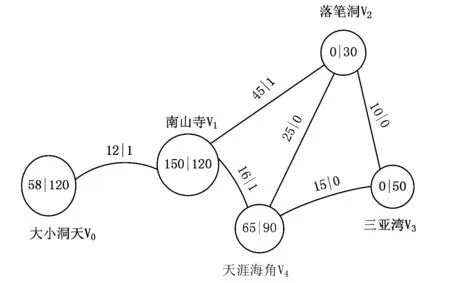
圖1 三亞主要景區景點示意圖

由圖的最短路徑的定義可知,要求圖1中某一個頂點(即景區/點)到其他頂點(即景區/點)的時間最少或費用最低問題,就轉換成了Dijkstra算法求最短路徑問題.由于景區/點門票價格和景點停留平均時間均為固定值,因此只需要利用經典Dijkstra算法計算出任意兩個景點間的最短路徑(路程或時間),即可計算出相應的最小費用及時間.假設用S,T,P分別表示景點至景點的最短路程,最短時間,最低費用;用s,t,p,gv,gp,pv,pp分別表示兩景點間直通距離、景點門票費、景點停留時間、高速公路平均速度、高速公路平均費用、普通公路平均速度、普通公路平均費,表示景點序號;k,z表示道路號,則有:

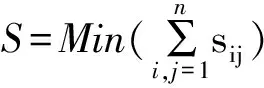
(1)

(2)

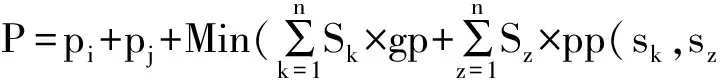
(3)

3 三亞旅游線路信息邏輯模型構建

經典Dijkstra算法中,要求圖的每條邊的權值和每個頂點的值有且只有一個值.為了實現每條邊(或頂點)的值有多個時,需借助于數據庫表的存儲功能, 所以Dijkstra算法運算時是基于數據庫表中的數據進行操作的.根據三亞市旅游景點情況,可建立如下4個數據庫表來存儲有關信息,其結構分別為如表1, 表2, 表3, 表4所示:

表1 道路信息

說明:[道路等級]分為普通公路0,平均速度為80km/h;高速公路1,平均速度為120km/h.假設任兩個景點間道路類型要么全為高速公路,要么全為普通公路.

表2 景點信息

說明:[景點停留平均時間]單位為分鐘;[景點門票]單位為元;[景點等級]分為0A-5A.

表3 景點連通信息

說明:[兩點間距]為0或-1時,表示兩點間無直通路,單位為公里;[方向描述]用始景點ID→終景點ID表示.

表4 最優臨時表

說明:本表中的數據只是程序運行時臨時產生, 程序關閉后其內容將被刪除.

4 算法設計與驗證

由于本研究是基于數據庫的Dijkstra算法應用,所以其求解最短路徑的過程更加復雜.首先封裝一個實現求解最短路徑Dijkstra類,當相關數據初始化完成后再調用此類中的Dijkstra方法求得最短路徑(路程、時間、費用),最后輸出結果.其程序流程如圖2所示.

為了驗證本算法的可行性,假設游客A從三亞灣出發到南山寺為例,其計算過程如下:

第一步:找出三亞灣至南山寺的所有線路,然后根據公式(2),先計算出所經道路所需要時間之和最少的道路,然后再加該道路上各景點的停留時間即可.

第二步:根據公式(3),先計算出所經道路所產生交通費之和最低的道路,然后再加上道上各景點門票費即可.

根據圖1,可知起點為三亞灣,終點為南山寺的線路總共有4條,每一條線路的總路程、所需時間和所需費用如表5所示.

表5 三亞灣->南山寺所有線路

從表5可知:選擇線路2,游客A所需時間和費用都最少.

為了方便游客選擇出行線路和管理者規劃旅游線路,本研究利用Microsoft SQL Sever2012數據庫存儲有關景點的數據和VB.NET語言編程實現計算過程.根據用戶選擇的起始景點、目標景點和優先方案,點擊查詢即可查看最佳線路.比如查詢從三亞灣至南山寺的最佳線路,程序運行效果如圖3所示:

圖3 程序運行效果

通過模擬測試,此程序運行效果與理論計算所得結果(表5所示)基本一致.

5 結語

盡管Dijkstra算法能夠求解城市旅游線路設計的一些最值問題,但其算法復雜度會隨著頂(節)點增多而增大,遍歷計算的頂(節)點越多,計算效率也會變得更低.另外,本研究局限于影響游客出行的兩個關鍵因素進行研究,沒有考慮諸如交通阻塞、自駕車、單行線、景點等級等其他因素對旅游線路選擇的影響,這是今后需要進一步完善的地方.

[1]孟慶偉,張冬姣. 基于Dijkstra最短路徑算法的優化及應用研究[J].電子商務,2014(12): 60-61.

[2]王一松,王直杰.基于實時交通信息的最優路徑規劃算法研究[J].計算機與現代化, 2013 (2):52-54.

[3]王樹西,吳政學.改進的Dijkstra最短路徑算法及其應用研究[J].計算機科學,2012,39(5):223-227.

[4]王佳,趙宏麗.基于Dijkstra算法的京津冀旅游交通線路優化研究[J].統計與決策,2011(13): 81-83.

[5]涂海麗.最短路徑算法及其應用探討[J].科技廣場,2011(9):11-14.

[6]齊信,楊泰平,段永坤,羅真富.基于MapX的Dijkstra算法在城市交通查詢中的實現[J].測繪與空間地理信息,2010(2): 136-139.

Application of the Dijkstra Algorithm in Sanya Tourist Route Planning

WANG Zhe-hea,LIN Yueb, ZHANG Qiaoc

(a.College of Computer Engineering; b. Mathematics Department; c. College of Tourism, Qiongzhou University, Sanya Hainan, 572022,China)

The minimum cost between any two specific scenic spots, the shortest time, the shortest distance are calculated by establishing mathematical model, applying database technology, and using the Dijkstra algorithm. Thus are provided the references for route selection and planning tourist routes.

Database; Dijkstra; shortestpath

2015-03-08

三亞市院地科技合作項目(2012YD29)；瓊州學院校級青年科學基金項目(QYQN201428)

王哲河(1980-),男,海南澄邁人,瓊州學院計算機工程學院計算機講師,碩士,研究方向為數據庫技術、信息化、算法應用研究等.

TP399;F224

A

1008-6722(2015) 05-0098-05

10.13307/j.issn.1008-6722．2015．05．21