基于遺傳算法的彈藥集裝模塊垛位優化*

任俊鵬 嚴 平 譚 波

(海軍工程大學兵器工程系 武漢 430033)

?

基于遺傳算法的彈藥集裝模塊垛位優化*

任俊鵬 嚴 平 譚 波

(海軍工程大學兵器工程系 武漢 430033)

垛位優化是彈藥庫房管理中的重要內容。論文首先對庫房中的彈藥集裝模塊的總搬運距離和各個垛堆的作業頻率建立多目標優化模型——彈藥集裝模塊垛位優化模型;然后采用權重系數變換法的遺傳算法對多目標問題進行優化計算,并結合實例給出了求解的具體步驟和操作過程。最后通過Matlab對實例尺寸為15m×10m×5m的庫房垛位優化進行計算,垛位優化初始解經過計算由最初的139.5697將降為132.5724。通過計算可知優化解的降幅達到了5.01%,證明了這一方法的有效性。

垛位優化; 集裝模塊; 遺傳算法

Class Number TJ410.3

1 引言

海軍彈藥保障正逐步擺脫“人推肩扛”的傳統保障模式,實現以托盤集裝箱為基礎的模塊化儲存和機械化搬運。托盤化的彈藥在進入彈藥庫房后,如何確定其在庫房中堆垛位置就成為一個關鍵的問題。垛位分配是否合理對今后彈藥的作業效率將產生直接的影響。如果彈藥集裝模塊的垛位分配合理,則有利于庫房中進行機械搬運作業,以提高彈藥保障效率;反之,就會出現不同規格的托盤彈藥的布局分散,常用彈藥和戰備彈藥的放置不合理等現象,這些因素對于彈藥的快速高效保障都是不利的。當前,我軍倉庫中儲存的箱裝物資在垛位選擇上還沒有詳細的方案,垛位的分配完全憑倉庫業務人員的經驗進行安排[1],在彈藥的堆垛過程中,對托盤的選擇以及垛位的順序則很少考慮,垛位被隨機排列,直接影響了收發作業的效率。鑒于此種現狀,彈藥庫房中的集裝模塊垛位優化問題開展研究對提高作業效率,增強戰時保障能力都具有重要意義。

2 彈藥垛位優化模型

在實際的倉庫儲存過程中,不能保證一個倉庫只對一種規格的彈藥托盤進行堆放。這就面臨著對一個倉庫中多種規格的彈藥托盤的堆放進行優化計算。既要確定一個倉庫中擺放何種規格的彈藥托盤,還要確定在該倉庫中各個規格的托盤數量和堆碼方式以及對不同彈藥的使用頻率和彈藥的儲備量來確定堆垛的位置,同時還要保證工作通道的寬度和位置設置的科學合理,從而使得每個垛位在收發過程中到門口的總路程L最短[2～3]。這樣才能提高倉庫的利用率和保障能力。

2.1 目標函數L

對整個彈藥庫房的儲存布局優化來說,就是保證每個垛堆中所有彈藥模塊單元的作業路程最小。所以其目標函數L為

Lmin=[F1+F2+F3+…+Fi]

(1)

2.2 子目標函數Fi

為保證庫房內每個垛位的托盤到門口的總路程最短,以倉庫的一個角建立三維直角坐標系,設一個倉庫中有l堆托盤,第i(i=1,2,3,…,l)堆垛中任一托盤的坐標為Vi=(x,i,y,i,z,i)m,n,g,距離函數Fi為第i堆中的所有托盤到門口的總路程。則:

(2)

其中,(i,m,n,g)表示第i堆的第m行,n列,g層的托盤。

2.3 各垛堆的權重系數

由于倉庫中儲存的彈藥品種和儲量不盡相同,且部隊對不同彈藥的需求量也不同。每一垛堆的彈藥品種、批次相同,根據不同的收發頻率和需求量設定第i堆的權重系數為Ki。垛堆的收發頻率越高[4],其權重系數Ki就越大,說明該垛堆應該擺放在靠近門口和主通道的位置,以便于快速、高效的收發作業。

2.4 約束條件

在軍用彈藥倉庫的存儲布局中,影響路徑優化的主要是通道的設置,如果通道的寬度和位置設置合理,就可以大大縮短作業路程和作業時間,提高作業效率。存儲區的通道主要是用于出入庫房作業的工作通道(包括機械搬運通道和手動叉車通道)和人員的檢查通道[5]。主通道連接彈藥倉儲區的進出口和各作業區域,手動叉車通道是連接主通道和各垛堆的通道,一般平行或垂直于主通道,不應與庫房墻壁臨近,檢查通道是相鄰垛堆之間通道,用于對彈藥的日常常規性檢查[6]。

通道寬度設計根據不同作業區域、人員或車輛行走速度、單位時間按通行人數、搬運物品體積等因素而定。為了滿足搬運機械的轉彎半徑和作業順暢,設定作業面T作≥4.2m,叉車通道T叉≥1.8m,為方便庫房的日常檢查,設定檢查通道T檢≥0.6m,為了保證機械作業的安全,垛堆的頂高距天花板的距離D通常大于等于0.5m[7～10]。即約束條件為

(3)

這樣才能保證機械搬運的順利作業,完成收發任務。

2.5 歸一簡化處理

根據彈藥庫房的堆垛原則,同一批次的彈藥和同一型號的托盤集中放置。在儲存布局的確定中,由于垛堆的層數g對于垛堆位置的設定不產生影響,而且在確定了垛堆的位置后,層數g對于作業路程L的影響也比較小。因此,為了簡化運算,將模型中堆垛層數設定為1層。

由式(2)可知,第i垛堆中的任一托盤坐標為Vi,因此Vi可簡化為(xi,yi,1)m,n,1。對于垛堆中的每個托盤的坐標可進行歸一化處理。由于每個垛堆的托盤的規格相同,所以垛堆的中心坐標V中為

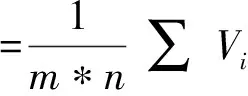
(4)

進而可以得到Fi的簡化

Fi=m*n*V中

(5)

即當確定了一個垛堆的托盤數和中心坐標后,便可以得到該垛堆所有集裝單元的作業路程總值。

2.6 模型表示

綜上所述,根據式(1)～式(5),彈藥庫的儲存布局數學模型為

Lmin=[k1*F1+k2F2+k3F3+…+klFl]

約束條件:

(6)

3 遺傳算法對實例問題的優化求解

3.1 選取算法類型

從上述模型建立過程中可以看出,對于彈藥存儲的集裝模塊優化問題是多目標優化問題,需要考慮多個目標函數的同時優化。根據本模型中的多目標優化,采用權重系數變換法來進行計算,根據各個垛堆不同的收發頻率和需求量等因素綜合設定權重系數Ki。將多目標優化問題化為單目標優化問題,進而求解多目標優化問題[11～12]。

3.2 實例計算

3.2.1 選定托盤規格

托盤是一種用于機械化裝卸、搬運和堆存貨物的集裝單元工具,GJB184A-1999《軍用立柱式托盤和箱式托盤基本尺寸和額定載重量》中規定了三種軍用托盤標準尺寸,分別是800mm×1200mm、1000mm×1200mm和1100mm×1100mm。

設定一地面庫長D=15m,寬W=10m,高為Z=5m,堆垛最多層數為G=3,為簡化計算,選擇規格為1200×1000×1300,1200×800×1300,1100×1100×1300的三種托盤來進行堆垛。為了保障堆碼的順利和收放作業的通暢,設定主作業面4.2m,檢查通道0.6m,叉車通道1.8m。托盤的堆放按照彈藥庫房的堆放原則擺放,保證彈體與通風口方向一致[13]。其堆垛樣式如圖1所示。

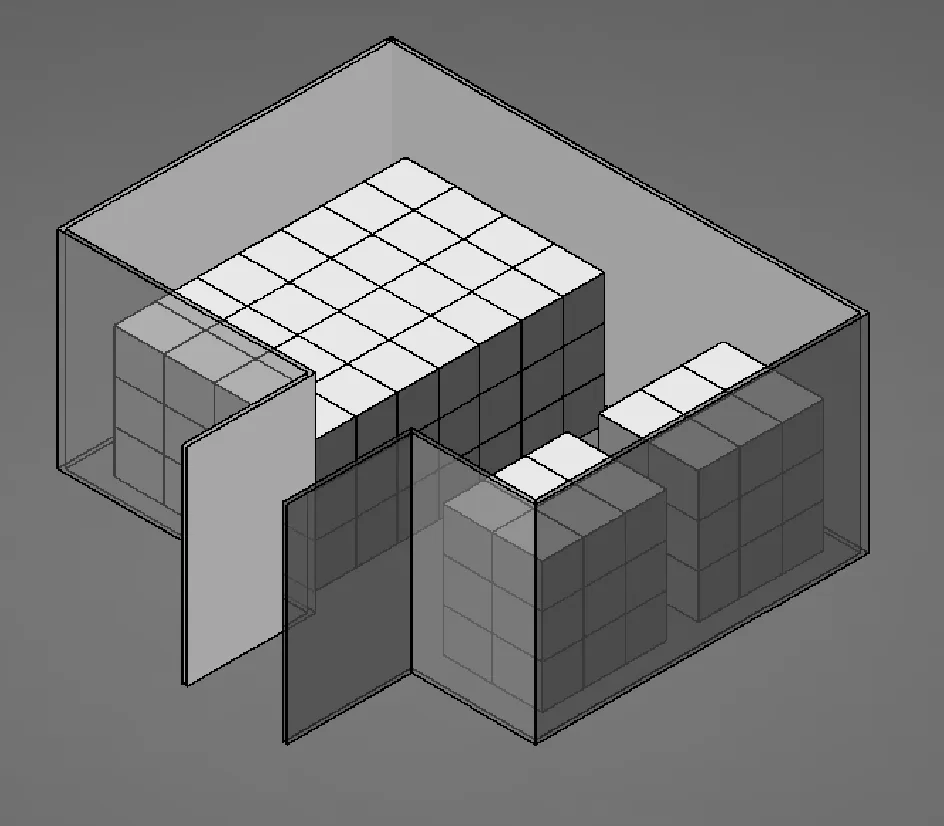
圖1 地面庫堆碼效果圖

3.2.2 數學模型表示

現對實例庫房中的集裝模塊垛位優化模型進行數學表達。設地面彈藥庫有一個出入口,庫房長15m,寬10m,高5m。現存三個垛堆,垛堆的托盤規格分別為:1200×1000×1300,1200×800×1300,1100×1100×1300三種。如圖2所示。

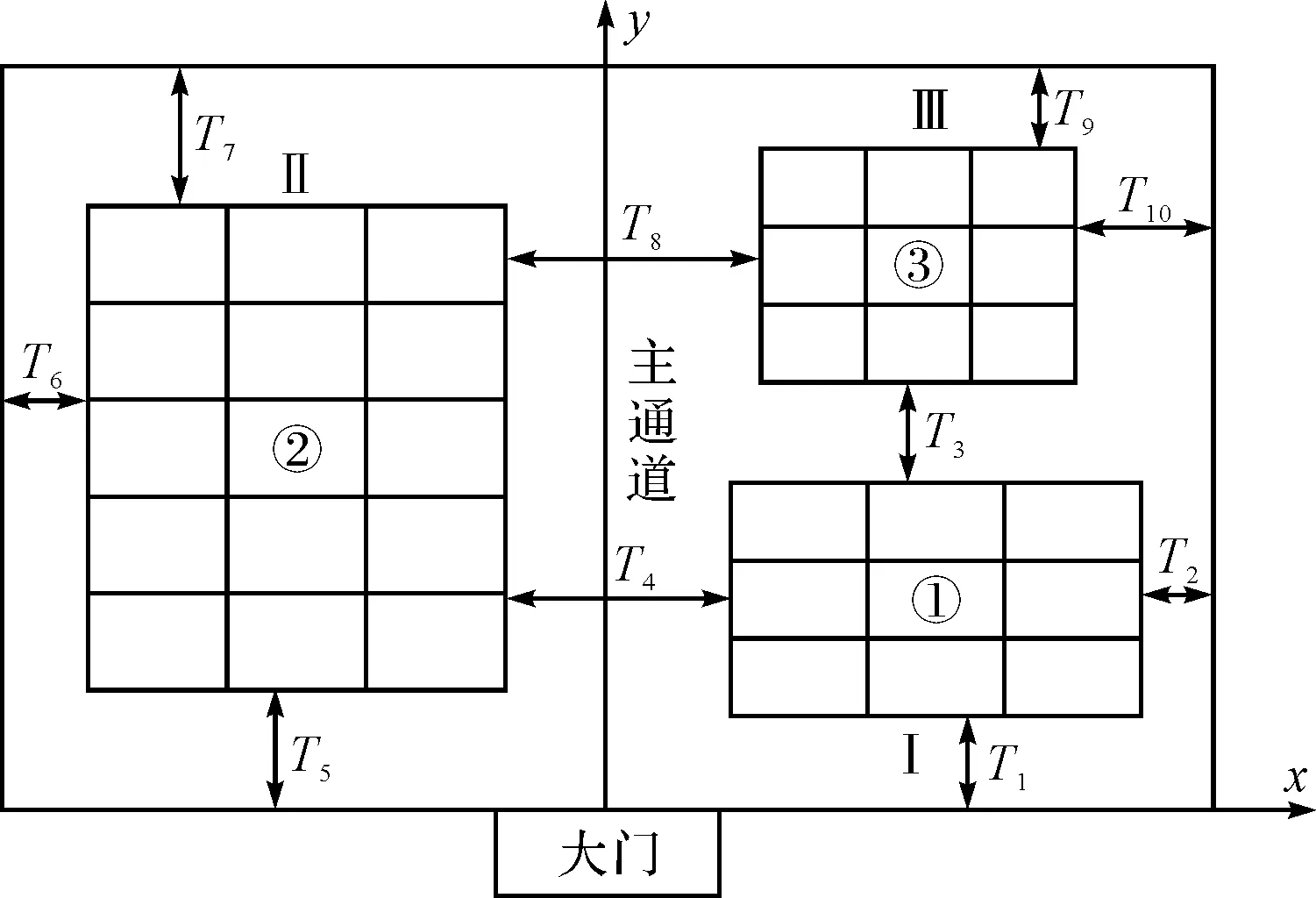
圖2 庫房儲存布局示意圖

其中,各垛堆的權重系數k1=0.7,k2=0.5,k3=0.3。編號為①、②、③的托盤分別為三個垛堆的中心托盤,設其坐標分別為V1(x1,y1),V2(x2,y2),V3(x3,y3)。則目標函數為

Lmin=[k1F1+k2F2+k3F3]

(7)

約束條件:

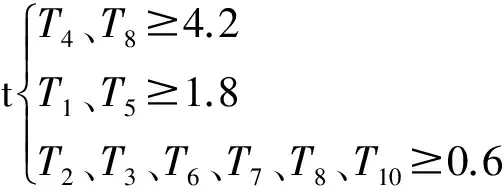
即:

Lmin=[k1F1+k2F2+k3F3]

(8)

3.3 具體算法步驟

· 第一步:編碼

在遺傳算法中最常用的編碼方式為二進制編碼,但是這種編碼方式不能較好地適用于貨位規劃這個多目標優化分配問題[14]。由于約束條件為實數區間,所以本文采用十進制實數編碼。染色體的編碼采用順序表達法,即根據集裝模塊單元的位置在庫房中的順序進行編碼。設定庫房中共有i個集裝模塊單元,每個單元的位置可以設定為(xi,yi),那么染色體的編碼為[(x1,y1)(x2,y2)(x3,y3)(x4,y4)…(xi,yi)],其示意圖如下:

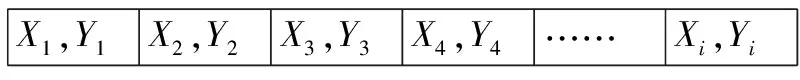
X1，Y1X2，Y2X3，Y3X4，Y4……Xi，Yi

在運算過程中為保證計算的精度,可以將染色體編碼轉換為二進制進行計算,再對計算結果轉換為十進制進行表示。

· 第二步:生成初始種群

根據約束條件,隨機生成數量為N的初始種群,作為垛位優化的初始解。

· 第三步:適應度函數

根據目標函數Lmin=[k1*F1+k2F2+k3F3+…+kiFi]以及權重系數ki計算出每個集裝模塊單元的最短路徑,因此,目標函數值越大,個體遺傳到下一代的概率就越小,即適應度越小。為了滿足目標值的優化要求,就要在選擇之前將個體目標函數轉化為適應值:

(9)

式中Cmax為一個適當的相對較大的數,這里定為L(x)的最大值。適應度函數的分配通過ranking函數計算,按照個體的目標值Lmin由小到大的順序進行對它們進行排序,使用線性評估,給最適應個體的適應度值為2,最差個體的適應度值為0。

· 第四步:選擇遺傳算子

在選擇遺傳算子時采用選擇比例算子。個體被選擇的概率由式(10)給出,

(10)

其中P(xI)為這個個體被選擇的概率,fi為個體的適應度值,∑fi為個體的適應度之和。

· 第五步:交叉、變異運算

在遺傳算法中,通常隨機選擇兩個個體進行交叉操作。通過交叉操作使得目標函數下的優良基因可以充分組合,以保證較大概率的找到目標函數的有化解。交叉概率的取值范圍一般是:0.4～0.99。

變異運算決定了遺傳算法的局部搜索能力。變異算子按照一定的概率(變異概率)選擇部分個體的部分染色體進行變異,被選定的個體按照隨機選擇的兩個垛位的位置進行相互對換,生成新的個體的同時又保持了種群的多樣性。交叉概率的取值范圍一般為:0.0001～0.1。

· 第六步:終止操作

遺傳算法的終止操作有很多種,本文采用設定遺傳的迭代代數。當遺傳迭代代數達到設定數值后,自動停止計算。否則繼續返回到第三步繼續運算,直到到達設定代數為止[15]。

3.4 通過Matlab編程對優化解進行表示

根據本文中的實例設定,可以通過Matlab編程進行運算。設定初始種群NIND=100;最大遺傳代數MAXGEN=50;代溝GGAP=0.9;交叉概率Px=0.7;變異概率Pm=0.02。計算50代后得到最優解如表2及種群均值變化的性能跟蹤如圖3所示。

表2 進化后的最優化解

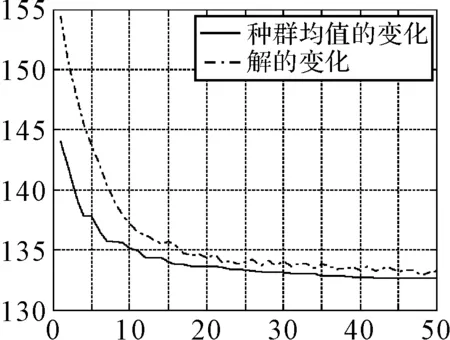
圖3 種群均值變化性能跟蹤圖

4 結果

通過以上計算可以看出,隨著遺傳代數的增加,最優解有了明顯的下降。經過50代的遺傳進化,最優解從最初的139.5697將降為132.5724,降幅達到了5.01%。對于垛堆的位置坐標也得到了最優解:(x1,y1)=(3.9051,3.0000),(x2,y2)=(3.9020,4.3019),(x3,y3)=(3.7513,6.4618)。在優化進程中,庫房中各個通道的寬度數據如表3所示,T3的初始值為0.0833,經過交叉變異30代后達到了0.4358,雖然有所提高,但仍不滿足要求。在50代時達到了0.7118(大于0.6),滿足了庫房作業通道的基本要求。以上數據計算表明通過遺傳算法該對解決垛位優化問題有較為明顯的效果。

表3 優化后的通道數值

5 結語

本文通過對現有彈藥倉庫的集裝化模塊彈藥垛位優化問題建立數學模型,選定合適規格的托盤,運用遺傳算法對彈藥倉庫垛位布局進行實例優化計算,通過Matlab編程計算得出集裝模塊彈藥垛堆的優化位置以及庫房的作業通道設置,在計算過程中,隨著遺傳進化代數的增加,可以看出總路程明顯的減少以及通道寬度的不斷優化,最終實現了彈藥跺位的優化,為提高倉庫作業效率和彈藥堆的合理布局提供了較為科學的依據。

[1] 馮濤,鐘敬武.貨位布局技術在后方倉庫中的研究與實現[J].計算機技術與自動化,2006,25(4):293-295.

[2] 陶英歌,郭乃林,羅紅英.基于遺傳算法的目標分配優化模型研究[J].系統工程與電子技術,2003:817-819.

[3] 魏國辰.物流機械設備的運用與管理[M].北京:中國物資出版社,2002,1:173-190.

[4] 賀鑫,馬振書,李良春,等.遺傳算法在箱裝軍用物資垛位優化中應用[J].科學技術與工程,2011,11(1):93-94.

[5] 朱子音.提高庫房利用率方法研究[D].長春:吉林大學碩士論文,2008:22-23.

[6] 劉昌祺.物流配送中心設施及設備設計[M].北京:機械工業出版社,2004,9:1-18,156-169.

[7] 李梅娟,陳雪波.Pareto遺傳算法在貨位配置中的應用研究[J].控制工程,2006:139-140.

[8] Stengel R F, Ray L R. Stochastic robustness of linear time-invariant systems[J]. IEEE Trans On Aut Control,1991,36(1):82-87.

[9] Ray L R, Stengel RF. AMont Carlo approachtothe analysisof control system robustness[J]. Automatica,1993,29(2):229-236.

[10] Carlos F M, Peter F J. An overview of evolutionary algorithmsin multiobjective optimization[J]. Evolutionary Computation,1995,3(1):1-16.

[11] 雷英杰,張善文,李續武,等.MATLAB遺傳算法工具箱及應用[M].西安:西安電子科技大學出版社,2011:45-61,107-118.

[12] 龔純,王正林.精通MATLAB最優化計算[M].北京:電子工業出版社,313-315.

Ammunition Container Module Stacking Location Optimization Based on Genetic Algorithm

REN Junpeng YAN Ping TAN Bo

(Department of Weaponry Engineering, Naval University of Engineering, Wuhan 430033)

Stacking location optimization is an important content of ammuniction warehouse management. Firstly, this paper establishes the warehouse of the module ammunition container tatal moving distance and the heap stacking location usage frequency multi-objecctive optimization model. Then, the weight coefficient transform method of multi-objective genetic algorithm is used for optimization calculation with true instance, and the specific steps and the operating process are given. Finally, the warehouse of the actual size of 15m×10m×5m optimizations are calculated by Matlab, and the optimization solution down from 139.569 to 132.5724, reduced by 5.01% which have proved the effectiveness of the proposed method.

stacking location optimization, containers module, genetic algorithm

2015年6月13日,

2015年8月1日

任俊鵬,男,碩士研究生,研究方向:武器系統運用與保障工程。嚴平,男,博士,副教授,研究方向:武器毀傷效能與彈藥設計。譚波,男,博士,講師,研究方向:彈藥工程。

TJ410.3

10.3969/j.issn.1672-9730.2015.12.030