多階段數量折扣訂貨模型優化與遺傳算法求解*

孫方東 李宗吉

(1.91183部隊 青島 266102)(2.海軍工程大學兵器工程系 武漢 430033)

?

多階段數量折扣訂貨模型優化與遺傳算法求解*

孫方東1李宗吉2

(1.91183部隊 青島 266102)(2.海軍工程大學兵器工程系 武漢 430033)

針對現有訂貨批量模型在描述庫存成本上的缺陷,對其進行了修正。應用遺傳算法對修正后的模型進行了求解,結合動態規劃最優性原理,著重優化了遺傳算法編碼方案的設計,確保編碼方案的完備性。經實例驗證,該求解方法可有效解決多階段數量折扣問題,克服了動態規劃和S-M法的局限性。

遺傳算法; 數量折扣; 訂貨策略

Class Number TP18

1 引言

供應商為刺激消費需求,減少產品積壓,加速資金流轉,通常會提供數量折扣,即購買商品的數量不同,商品單價也不同,一般情況下購買數量越多,單價越低。在這種情況下,從買方的角度,就需確定其經濟合理的訂貨策略使其成本降低。這是一類典型的動態批量問題,其求解的基本思路是建立描述具體問題的線性或非線性規劃模型,并運用一定的算法求解。現有的規劃模型[5～8]結構均比較相似,但存在對目標函數中庫存成本表達不完善的缺陷。

求解算法中比較常用的是Sliver&Meal啟發式算法(S-M)、拉格朗日松弛解法、動態規劃法(DOQ)和啟發式算法[2]。文獻[3～4]雖指出S-M法有可能收斂到局部最優,并提出了各自的解決方案,但并未從根本上解決此問題。DOQ模型基于對最優解結構屬性的證明,大大縮小了可行解的空間范圍,是求解動態批量問題的最核心和基礎的方法,但DOQ模型對目標函數和約束條件及問題背景均有一定要求[2]。且隨著多級多項目多資源問題的引入,動態規劃作為精確求解方法很難在短時間內取得滿意解。

本文首先修正了現有模型中庫存成本的表達式,使其更符合實際情況,進而應用遺傳算法對模型進行了求解。基于該類問題最優解的性質[8],結合動態規劃最優性原理,著重優化了遺傳算法編碼方案的的設計,確保編碼方案可遍歷各可行解,進而收斂到全局最優。結合文獻[4,7]中的兩個案例,進行了實例計算,計算結果表明,本文提出的優化算法有更好的效果。

2 模型建立

訂貨批量問題屬于多周期規劃問題,將規劃期分成不同的時間周期,基于不同周期的需求,綜合權衡購買成本、訂貨準備成本和庫存成本。優化目標為在恰當的時間購買恰當數量的產品,使相關總成本最小。設周期性檢查庫存,只在期初訂貨,其訂貨量為xi,提前期固定,不允許缺貨。計劃時段為n個周期,計劃期開始時和結束時庫存都為零。成本包括購買成本、訂貨成本和庫存成本。已有文獻[5～8]在建立該問題的模型時,目標函數多采用如下所示的形式:

(1)

式(1)中及下文將用到的各符號代表的物理意義如表1所示。

表1 各符號物理意義

目標函數中第一項為購買成本,第二項為庫存管理成本,第三項為訂貨成本。考察式(1)中的庫存管理成本,該表示方法規定了庫存管理成本僅由期末剩余的庫存所決定,而沒有考慮逐步消耗的備件同樣會帶來管理成本,這顯然是不合理的。考慮一個極端情形,設第i時間段開始時的訂貨在期末恰好用完,該時間段庫存Ii=0,則庫存管理成本為零,顯然不符合實際。因此用hi·Ii計算庫存管理成本是不合適的。

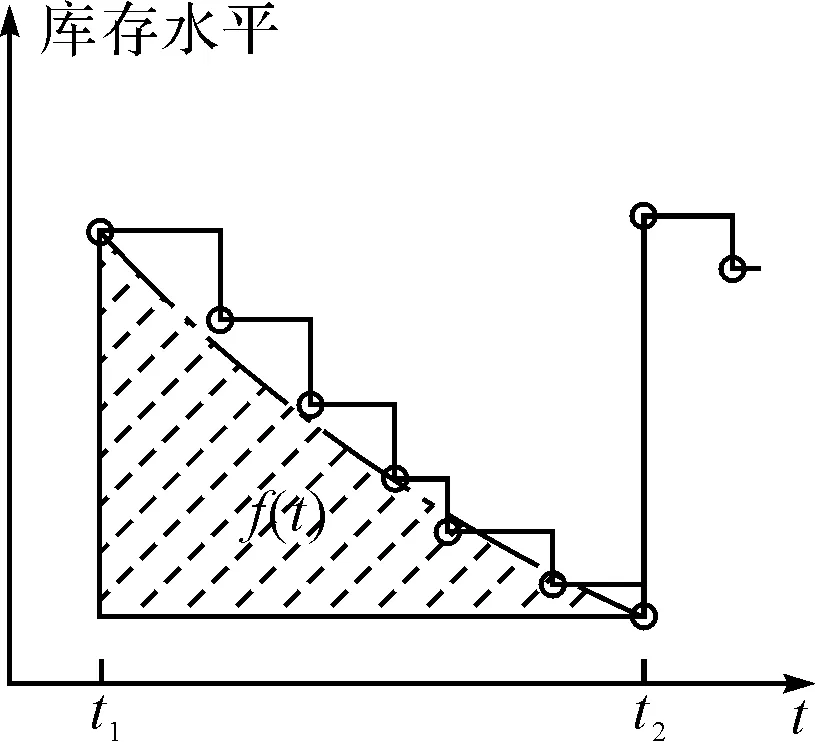
圖1 物資消耗過程

考察物資消耗過程如圖1所示。

(2)

考慮一種較特殊的情形,備件消耗速度不變,這在短周期內是可以接受的。設第i時間段內需求為di,則由需求引起的平均庫存為di/2,加上未消耗完的庫存即為該時間段的總體平均庫存水平,庫存成本為hi·(Ii+di/2),本文即在該種情形下建立模型。

（1）無雙重支付的情形。假設A有1枚比特幣，要將其轉給B。A首先構造一筆交易Tx1：使用私鑰簽署該筆交易，并將交易單Tx1廣播出去。其他實體收到信息后，通過UTXO索引計算A是否有能力支付1枚比特幣，如果有能力支付，則認為此次交易是合法。最后，A的錢包地址減少1枚比特幣，B的錢包地址增加1枚比特幣。

重新建立模型如下:

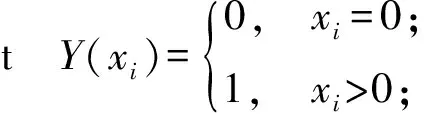
Ii=Ii-1+xi-di

∑xi=∑di

(3)

訂貨序列x={xi,i=1,2,…,n}即為決策變量。

3 算法設計

1) 最優解的性質

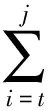
2) 應用遺傳算法求解的思路

遺傳算法的操作對象是與決策變量相對應的編碼,問題的關鍵在于選取合適的操作變量,構造合理的編碼方案,使得編碼方案具有完備性和非冗余性,即遺傳算法空間中的染色體能對應所有問題空間中的候選解,并盡可能縮小尋優空間。文獻[6]提出將每期的訂貨量作為操作變量,采用實值編碼方案。該方案物理意義明確,但問題實質上是只有第一期和最后一期為再生點的特殊情況。同時產生隨機個體的方法會產生大量無意義的冗余方案,造成了計算資源的浪費。文獻[7]將Y(xi)作為操作變量,采用二進制編碼。不存在折扣時,Y(xi)與訂貨量存在一一對應的關系,可以方便的進行轉化,不失為一種具備完備性和非冗余性的好方法。本文中的第一個案例,即采取該方案得到了理想的結果。但存在折扣時,決策變量訂貨量有可能是折扣點,也有可能是實際需求量,與Y(xi)沒有一一對應關系,因此該編碼方案不能解決存在折扣的問題。其提出的案例雖然帶有折扣,但實際按照無折扣進行近似優化,得到的結果不一定是最優。本文在實例計算中對其中的一個案例進行重新優化,得到了更為理想的結果。

本文的編碼方案如下:

設有兩個相鄰的再生點Zj、Zk,構造算法如下:

Step 1:i=1:length(j+1:k)

if length(j+1:k)=1,則j+1期訂貨量為實際需求量;

if length(j+1:k)>1,進入step 2;

Step 2:按照帶折扣問題可行解的性質,對每一階段產生一個可行解矩陣,代表該階段所有的子策略。可行解矩陣每一行為一個可行解,其中第一行可行解的最后一次訂貨小于最小的折扣點,則第l行可行解的最后一次訂貨是第一行可行解最后l次訂貨量之和。以某一階段中有三個訂貨點為例,可能的可行解矩陣結構如下所示:

其中x1、x2、x3是三個訂貨量不為零的訂貨點,訂貨點的訂貨量須滿足最優解性質。此時問題的關鍵為如何實現第一行解的構造,本文中第一行可行解的產生程序框圖如圖2所示。

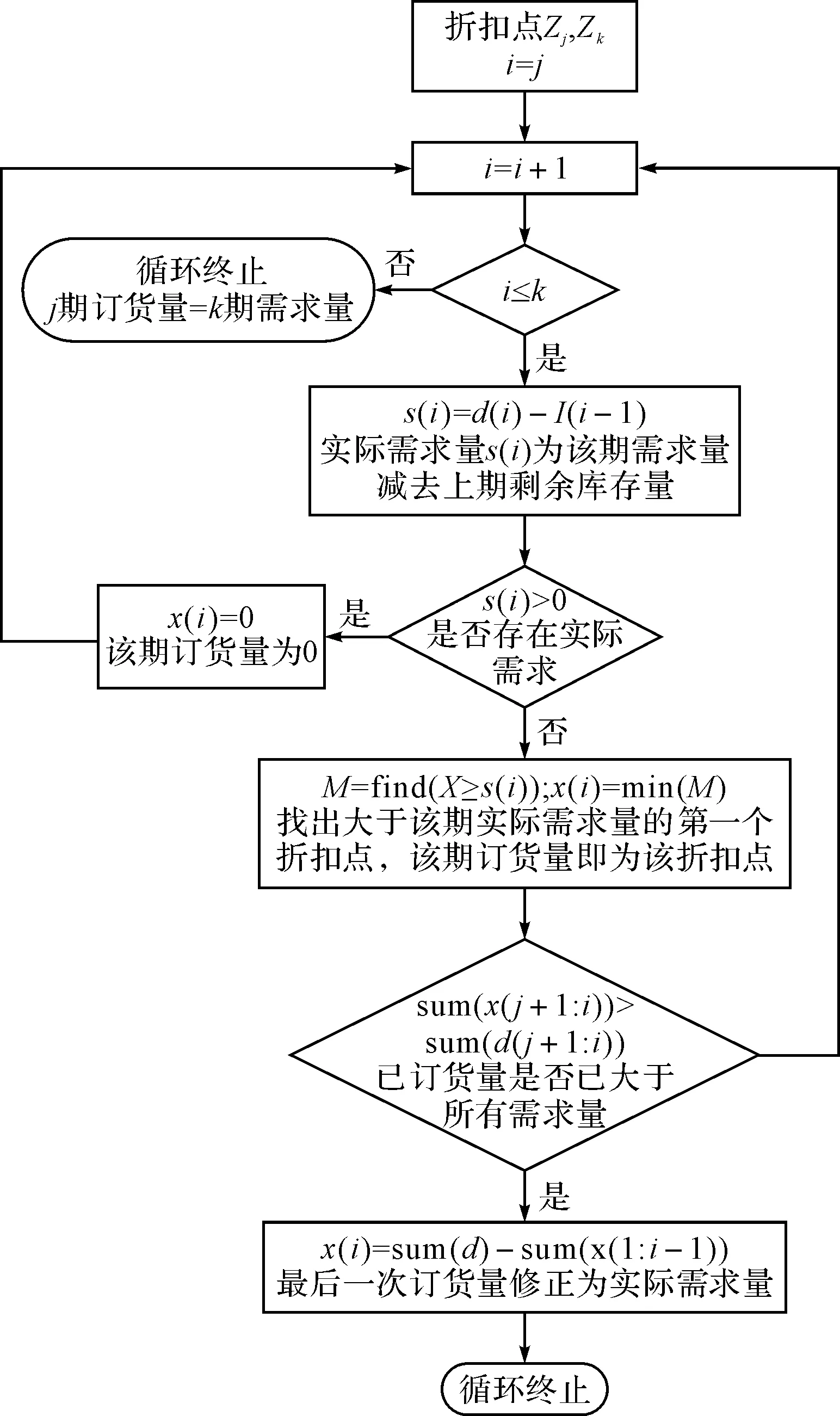
圖2 第一行解產生程序框圖

4 實例計算

例1首先考察無折扣時的優化策略,取文獻[4]中應用S-M法優化訂貨策略的案例,簡便起見,僅取其數據,并去掉量綱。其需求數據如表3所示,其中訂貨費用為1200,儲存費用為50。

表3 物資需求數據

分別應用動態規劃和遺傳算法進行優化,計算結果如表4所示。

表4 訂貨策略優化結果

DOQ及遺傳算法優化策略的到貨點在周期1、4、7,訂貨數量分別為12、24、17,得到總成本費用為8000。S-M法得到的優化策略到貨點分別為1、4、8,訂貨數量分別為12、27、14總成本費用為8250。說明本文提出的方法不僅是有效的,而且優于S-M法,能收斂到全局最優。

由于帶折扣問題涉及多個變化的參數,狀態空間龐大,難以采用動態規劃法驗證本文提出的方法是否收斂到全局最優,故本節選取文獻[7]中案例,對同一案例進行優化,進而比較兩者結果。

例2取文獻[7]中的案例,同樣取其數據,去掉量綱。其中產品1的需求為[50,45,35,60],折扣點為[100,300],單價分別為[12,10,8],訂貨成本分別為[10,11,12,10],儲存成本為[0.5,0.4,0.6,0.5]。文獻[7]中的方法一與本文提出的方法二計算結果對比如表5所示。

表5 計算結果對比

可以看到,本文提出的方法得到的總費用較少。進一步分析結果,本文的計算結果導致一次性大量訂貨,觀察儲存成本與單價,發現產品1的儲存成本僅占單價的5%,一次性大量訂貨是可以接受的,若考慮其他資源的約束,如資金、庫存容量等限制,則要另外建立模型加以分析,就本案例,本文提出的解決方法是較優的。

5 結語

本文首先對帶折扣批量訂貨問題模型進行了修正,使其更符合實際情況。進而基于該類問題最優解的性質,應用遺傳算法對該問題進行了求解,結合動態規劃最優性原理,著重優化了編碼方案的設計,確保算法可收斂到全局最優。同時遺傳算法作為啟發式算法,在求解大型問題時比動態規劃法有更好的尋優速度。此外,遺傳算法構造簡單,可方便地進行拓展以解決更復雜的問題。計算結果也驗證了本文提出的方法的有效性,可對工程實踐給予指導。

[1] 徐健騰,張慶普.多供應商的動態批量問題研究[J].哈爾濱工程大學學報,2010,31(4):451-456.

[2] 王海英,等.基于動態規劃方法的動態批量問題研究[J].科技進步與對策,2009,26(4):162-165.

[3] 金錫萬.多階段需求不均衡時的一種庫存控制模型-兼評Silver&Meal啟發式算法I[J].物流技術,1995(6):15-18.

[4] 唐納德·沃爾特斯著.李習文,李斌譯.庫存控制與管理[M].北京:機械工業出版社,2005:82-86.

[5] 唐立新,楊自厚,王夢光,等.CIMS中帶多資源的CLSP問題的遺傳啟發式算法[J].系統工程理論與實踐,1997(4):39-44.

[6] 王建忠,杜綱.基于遺傳算法的數量折扣訂貨模型求解[J].河北工業大學學報,2006,35(2):81-85.

[7] 田俊峰,楊梅.數量折扣條件下的動態訂貨批量優化[J].西南交通大學學報,2004,39(5):595-599.

[8] 徐健騰,張慶普.多供應商的動態批量問題研究[J].哈爾濱工程大學學報,2010,31(4):451-457.

[9] Shittu, E. (2003). Applying genetic algorithms to the deterministic time-varying fixed quantity lot sizing problem[D]. Masters Thesis. Cairo, Egypt: The American University in Cairo.

[10] Lotfi Gaafar. Applying genetic algorithms to dynamic lot sizing with batch ordering[J]. Computers & Industrial Engineering,2006(51):433-444.

Optimization for Multi-period Ordering Model with Quantity Discount and Solving Based on GA

SUN Fangdong1LI Zongji2

(1. No. 91183 Troops of PLA, Qingdao 266102) (2. Naval Research Institute of New Weaponry Technology & Application, Naval University of Engineering, Wuhan 430033)

The model describing the ordering problem with quantity discount is modified to be true of the reality. And a method was proposed based on Genetic Algorithms, especially the coding method is optimized to get the best result. Using certain numerical examples, the method is proved to be effecter than S-M and DOQ.

GA, quantity discount, order tactics

2015年6月11日,

2015年7月26日

孫方東,男,助理工程師,研究方向:水中兵器動力推進技術。

TP18

10.3969/j.issn.1672-9730.2015.12.031