基于人工神經(jīng)網(wǎng)絡(luò)模型的地下水水位動(dòng)態(tài)變化模擬
魏光輝
(新疆農(nóng)業(yè)大學(xué)水利與土木工程學(xué)院,烏魯木齊 830052)
文章編號(hào):1006—2610(2015)03—0006—04
基于人工神經(jīng)網(wǎng)絡(luò)模型的地下水水位動(dòng)態(tài)變化模擬
魏光輝
(新疆農(nóng)業(yè)大學(xué)水利與土木工程學(xué)院,烏魯木齊 830052)
地下水水位的預(yù)測(cè)在流域地表水和地下水資源的綜合規(guī)劃管理中起著非常重要的作用。在該研究中,人工神經(jīng)網(wǎng)絡(luò)模型被應(yīng)用于希尼爾水庫(kù)周邊地下水水位的預(yù)測(cè)中。采用研究區(qū)6口地下水觀測(cè)井資料,用人工神經(jīng)網(wǎng)絡(luò)模型進(jìn)行模擬預(yù)測(cè)1周后的地下水水位。模型輸入因子包括此前1周蒸發(fā)量、水庫(kù)水位、排渠水位、抽水量和觀測(cè)井地下水位,因此模型有15個(gè)輸入節(jié)點(diǎn)和6個(gè)輸出節(jié)點(diǎn)。將3種不同的神經(jīng)網(wǎng)絡(luò)訓(xùn)練算法,即自適應(yīng)學(xué)習(xí)速率動(dòng)量梯度下降反向傳播算法(GDX)、LM算法和貝葉斯正則化算法(BR)用于地下水水位預(yù)測(cè),并對(duì)模擬結(jié)果進(jìn)行了評(píng)估。結(jié)果表明:3種神經(jīng)網(wǎng)絡(luò)訓(xùn)練算法在研究區(qū)地下水水位預(yù)測(cè)中表現(xiàn)均較好。然而,BR算法的性能總體略優(yōu)于GDX和LM算法。將BR算法訓(xùn)練的人工神經(jīng)網(wǎng)絡(luò)模型用于預(yù)測(cè)研究區(qū)未來(lái)2、3和4周的地下水水位,雖然地下水位預(yù)測(cè)的準(zhǔn)確性隨著時(shí)間的增加有所降低,但模擬效果仍然較好。
人工神經(jīng)網(wǎng)絡(luò);地下水位預(yù)測(cè);GDX算法;LM算法;BR算法
0 前 言
地下水是一種寶貴的自然資源,并已成為世界上所有氣候區(qū)域的可依賴水源[1]。在發(fā)展中國(guó)家,由于地下水可直接輸送到貧困區(qū)、更具成本效益以迅速便捷程度超過(guò)地表水,故開(kāi)發(fā)地下水已成為一種扶貧的工具[2]。然而,由于地下水資源的過(guò)度開(kāi)發(fā),加上越來(lái)越多的地下水污染,導(dǎo)致地下水水位下降和含水層枯竭,這嚴(yán)重威脅了供水和生態(tài)系統(tǒng)的可持續(xù)性。許多非可持續(xù)利用地下水的后果日趨明顯,世界各地,特別是在發(fā)展中國(guó)家,都在關(guān)注如何從含水層獲得一個(gè)長(zhǎng)期的可持續(xù)地下水量[1,3-5]。因此,水資源的可持續(xù)管理特別是地下水資源的可持續(xù)管理是目前及今后一個(gè)時(shí)期需要亟待解決的問(wèn)題。
目前,地下水建模已成為一種強(qiáng)大的工具來(lái)幫助水資源管理者,優(yōu)化地下水的使用,進(jìn)而保護(hù)這一重要資源。在過(guò)去的幾年中,基于數(shù)值模型的物理方法被應(yīng)用于地下水系統(tǒng)的模擬和分析。隨著計(jì)算機(jī)技術(shù)的廣泛使用,這種方法正在被越來(lái)越多的水文地質(zhì)工作者和環(huán)保工作者所使用,并且已經(jīng)將應(yīng)用范圍從地下水含水層的安全產(chǎn)量分析擴(kuò)展到地下水污染整治等問(wèn)題。在大多數(shù)發(fā)展中國(guó)家,由于資料匱乏,使用基于物理方法的數(shù)值模型受到很大限制。因此,在這種情況下,經(jīng)驗(yàn)?zāi)P统蔀橐粋€(gè)有吸引力的模型——因?yàn)樗鼈兛梢蕴峁┹^為有用的結(jié)果,且具有所需資料較少的特點(diǎn)。人工神經(jīng)網(wǎng)絡(luò)(ANN)模型就是此類(lèi)模型中的一種,它非常適合于非線性動(dòng)態(tài)系統(tǒng)建模[6],且不需要對(duì)物理性質(zhì)進(jìn)行明確的定性和定量,并能解決大規(guī)模的復(fù)雜問(wèn)題[7]。目前它已用于降雨徑流模型,降水預(yù)報(bào)、河流流量建模、蒸散量建模、水質(zhì)和地下水建模等[6,8-9]。與地表水水文研究相比,人工神經(jīng)網(wǎng)絡(luò)在地下水水文學(xué)中的應(yīng)用數(shù)量相對(duì)較少。在地下水水文學(xué)中,神經(jīng)網(wǎng)絡(luò)技術(shù)已用于含水層參數(shù)估計(jì)[10-12],地下水水質(zhì)預(yù)測(cè)[13-14],地下水水位預(yù)測(cè)[15-17]。以往關(guān)于地下水水位預(yù)測(cè)的研究中,人工神經(jīng)網(wǎng)絡(luò)模型主要用于單井預(yù)測(cè),即使用1組輸入?yún)?shù)預(yù)測(cè)地下水水位。然而,在目前研究中,通過(guò)使用人工神經(jīng)網(wǎng)絡(luò)模型來(lái)同時(shí)預(yù)測(cè)井群的地下水水位已成為當(dāng)務(wù)之急。本文將人工神經(jīng)網(wǎng)絡(luò)模型與自適應(yīng)學(xué)習(xí)速率動(dòng)量梯度下降反向傳播算法(GDX)、L-M算法和貝葉斯正則化算法(BR)相結(jié)合,用于希尼爾水庫(kù)周邊地區(qū)地下水井群水位預(yù)測(cè),這對(duì)于新疆的地下水開(kāi)發(fā)利用具有極其重要的參考價(jià)值。
1 研究區(qū)概況
希尼爾水庫(kù)位于新疆庫(kù)爾勒市境內(nèi),地理坐標(biāo)介于86°13′~86°18′E,41°33′~41°38′N(xiāo)。水庫(kù)從孔雀河第一分水樞紐引水,是經(jīng)庫(kù)塔干渠總干渠輸水的注入式大(2)型平原水庫(kù)。由于水庫(kù)蓄水,勢(shì)必將導(dǎo)致周邊地下水位在一定程度上的上升。鑒于此,希尼爾水庫(kù)在2000年建設(shè)之初,就在周邊區(qū)域布設(shè)了地下水觀測(cè)井,進(jìn)行周邊區(qū)域的地下水水位觀測(cè)。
本文以希尼爾水庫(kù)下游的庫(kù)爾勒市西尼爾村為研究區(qū),對(duì)研究區(qū)的觀測(cè)井地下水位進(jìn)行分析預(yù)測(cè)。研究區(qū)一共布置了6口地下水位觀測(cè)井,觀測(cè)井位置示意見(jiàn)圖1。研究區(qū)農(nóng)業(yè)灌溉用水主要來(lái)自于地下水,并有少量地表水作為補(bǔ)充灌溉。目前該區(qū)域共有12口井用來(lái)灌溉,這些井的建設(shè)及管理由當(dāng)?shù)氐挠盟畱魠f(xié)會(huì)統(tǒng)一負(fù)責(zé)。

圖1 希尼爾水庫(kù)及觀測(cè)井位置示意圖
2 材料與方法
2.1 數(shù)據(jù)來(lái)源
本研究的數(shù)據(jù)來(lái)源來(lái)自希尼爾水庫(kù)2005年1—12月共計(jì)52組觀測(cè)井水位資料及同期的氣象(降水、蒸發(fā))、水庫(kù)水位、排渠水位等資料。
2.2 神經(jīng)網(wǎng)絡(luò)算法概述
人工神經(jīng)網(wǎng)絡(luò)是一個(gè)并行分布式信息處理系統(tǒng)[18],類(lèi)似于人腦中的生物神經(jīng)網(wǎng)絡(luò)。本文采用前饋式神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)結(jié)合自適應(yīng)學(xué)習(xí)速率動(dòng)量梯度下降反向傳播算法(GDX)、LM算法和貝葉斯正則化算法(BR)進(jìn)行模擬效果比較[19],以確定合適的算法來(lái)進(jìn)行研究區(qū)地下水水位預(yù)測(cè)。
2.2.1 前饋神經(jīng)網(wǎng)絡(luò)
在前饋神經(jīng)網(wǎng)絡(luò)中,節(jié)點(diǎn)一般都安排在層上,從第1個(gè)輸入層開(kāi)始,并在最后1個(gè)輸出層結(jié)束。它可以有幾個(gè)隱藏層,每1層又有1個(gè)或多個(gè)節(jié)點(diǎn)(BP神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)見(jiàn)圖2)。信息從輸入層傳遞到輸出端。第1層的節(jié)點(diǎn)將連接到下一層,但不是在一層。因此,輸出層的每一個(gè)節(jié)點(diǎn)只依賴于上一個(gè)輸入層節(jié)點(diǎn)及對(duì)應(yīng)的權(quán)值。前饋神經(jīng)網(wǎng)絡(luò)的主要優(yōu)勢(shì)是易掌握,可以逼近任意輸入、輸出層[20]。

圖2 BP神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)圖
2.2.2 訓(xùn)練算法
(1) 自適應(yīng)學(xué)習(xí)速率動(dòng)量梯度下降反向傳播算法(GDX)
在標(biāo)準(zhǔn)BP算法中,算法結(jié)果對(duì)于學(xué)習(xí)速率的設(shè)置非常敏感[21-22]。為了克服這個(gè)問(wèn)題,GDX算法結(jié)合自適應(yīng)學(xué)習(xí)率與動(dòng)量訓(xùn)練。自適應(yīng)學(xué)習(xí)率試圖保持盡可能大的學(xué)習(xí)步長(zhǎng),同時(shí)保持學(xué)習(xí)的穩(wěn)定。每個(gè)變量根據(jù)動(dòng)量梯度下降進(jìn)行調(diào)整。這就像一個(gè)低通濾波器,動(dòng)量允許網(wǎng)絡(luò)忽略錯(cuò)誤表面的小功能。該訓(xùn)練算法是最簡(jiǎn)單、最常見(jiàn)的訓(xùn)練算法[23-24]。
(2) L-M算法
傳統(tǒng)的BP算法在進(jìn)行網(wǎng)絡(luò)訓(xùn)練時(shí),往往會(huì)陷入某個(gè)局部最小點(diǎn)。L-M算法使每次迭代不再沿著單一的負(fù)梯度方向,而是允許誤差在梯度下降法和高斯-牛頓法之間自適應(yīng)調(diào)整網(wǎng)絡(luò)權(quán)值,使網(wǎng)絡(luò)有效收斂,大大提高了網(wǎng)速的收斂速度和泛化能力[25]。
L-M優(yōu)化算法權(quán)值調(diào)整公式[26]:
x(i+1)=xi-[JTJ+μI]-1JTe
(1)
式中:x為神經(jīng)網(wǎng)絡(luò)權(quán)值;J為誤差對(duì)權(quán)值微分的雅可比矩陣;μ為控制學(xué)習(xí)過(guò)程的一個(gè)標(biāo)量;e為殘余誤差向量。當(dāng)標(biāo)量μ為零時(shí),就成為牛頓法;當(dāng)標(biāo)量μ增加時(shí),等式就成為小步長(zhǎng)梯度下降法。由于牛頓法具有運(yùn)算速度更快、更準(zhǔn)確、更接近誤差最小值的特點(diǎn)。
(3) 貝葉斯正則化算法
貝葉斯正則化算法涉及優(yōu)化的目標(biāo)函數(shù),它包括傳統(tǒng)的平方和誤差函數(shù)以及一個(gè)稱(chēng)為“管理者(regularizer)”的函數(shù)。貝葉斯正則化算法能夠使最優(yōu)權(quán)值衰減參數(shù)在訓(xùn)練期間自動(dòng)進(jìn)行調(diào)整[27]。
2.3 BP神經(jīng)網(wǎng)絡(luò)設(shè)計(jì)
在Matlab R2011a中,BP神經(jīng)網(wǎng)絡(luò)設(shè)計(jì)包括網(wǎng)絡(luò)的生成、訓(xùn)練及仿真可以通過(guò)調(diào)用一系列函數(shù)來(lái)實(shí)現(xiàn)[28-29]。
由于水庫(kù)周邊地下水水位變化規(guī)律具有明顯的周期特征。因此,對(duì)該時(shí)間序列進(jìn)行模擬時(shí),采用前i個(gè)點(diǎn)值來(lái)得到第i+1個(gè)點(diǎn)值的方法。通過(guò)自相關(guān)分析,達(dá)到顯著水平(a=0.05)的本周地下水埋深與前一周的地下水埋深有關(guān)。同時(shí),通過(guò)相關(guān)分析選取了前一周水庫(kù)平均水位、平均蒸發(fā)量、排渠水位與抽水量作為模型輸入節(jié)點(diǎn)(即輸入因子)。因此,模型輸入節(jié)點(diǎn)共計(jì)15個(gè),輸出節(jié)點(diǎn)為6個(gè)(6口觀測(cè)井的地下水位)。
2.4 評(píng)價(jià)標(biāo)準(zhǔn)
本文采用相關(guān)系數(shù)(R)、平均偏差(bbias)、均方根誤差(RRMSE)與納什效率(Nash-Sutcliffe efficiency,EN-S)來(lái)評(píng)價(jià)模型計(jì)算結(jié)果,各評(píng)價(jià)指標(biāo)計(jì)算式如下[30]:
(2)
(3)
(4)
(5)
3 結(jié)果與討論
3.1 人工神經(jīng)網(wǎng)絡(luò)訓(xùn)練算法評(píng)價(jià)
在人工神經(jīng)網(wǎng)絡(luò)模型進(jìn)行預(yù)測(cè)前,先要對(duì)模型進(jìn)行訓(xùn)練。本模型輸入節(jié)點(diǎn)共計(jì)15個(gè),輸出節(jié)點(diǎn)為6個(gè)(6口觀測(cè)井),以該模型來(lái)預(yù)測(cè)研究區(qū)下一周的地下水水位。各種算法模型最優(yōu)隱含神經(jīng)元個(gè)數(shù)的計(jì)算結(jié)果見(jiàn)表1。
由表1可以看出,各種算法模型最優(yōu)隱含神經(jīng)元個(gè)數(shù)中,L-M算法所需隱含神經(jīng)元個(gè)數(shù)最少,為20個(gè),BR算法所需隱含神經(jīng)元個(gè)數(shù)最多,為40個(gè)。
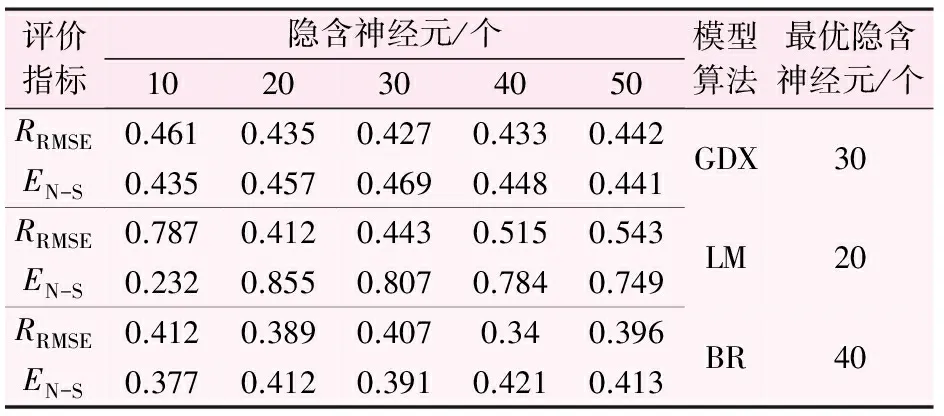
表1 模型隱含神經(jīng)元個(gè)數(shù)計(jì)算表
根據(jù)希尼爾水庫(kù)管理處提供的2005年1月—2005年12月共計(jì)52組觀測(cè)井水位資料及同期的氣象(降水、蒸發(fā))、水庫(kù)水位、排渠水位等資料,通過(guò)神經(jīng)網(wǎng)絡(luò)模擬訓(xùn)練,得到1周后研究區(qū)地下水位不同算法下的評(píng)價(jià)指標(biāo)值(見(jiàn)表2)。

表2 不同算法下的評(píng)價(jià)指標(biāo)值對(duì)比表
由表2可以看出,不同算法模型各項(xiàng)評(píng)價(jià)指標(biāo)計(jì)算值相差不大,但以BR算法略優(yōu)于GDX算法與LM算法。
3.2 研究區(qū)地下水位的預(yù)測(cè)
本文選取研究區(qū)前一周水庫(kù)平均水位、平均蒸發(fā)量、排渠水位與抽水量作為模型輸入節(jié)點(diǎn)(即輸入因子),利用BR算法,對(duì)未來(lái)2、3、4周的地下水位進(jìn)行預(yù)測(cè)分析。因此,模型輸入節(jié)點(diǎn)仍然為15個(gè),輸出節(jié)點(diǎn)為6個(gè)(6口觀測(cè)井)。
考慮到篇幅所限,本文以1號(hào)井與5號(hào)井為例,利用評(píng)價(jià)指標(biāo)對(duì)模型預(yù)測(cè)值進(jìn)行評(píng)價(jià)(見(jiàn)表3)。

表3 不同預(yù)測(cè)時(shí)間段模型擬合效果評(píng)價(jià)表
由表3可以看:① 隨著預(yù)測(cè)時(shí)間的推移,模型預(yù)測(cè)精度有降低的趨勢(shì);② 盡管模型預(yù)測(cè)精度有所降低,但是其精度仍然滿足實(shí)際需要,具有可信性。
綜上所述,經(jīng)過(guò)算法改進(jìn)的人工神經(jīng)網(wǎng)絡(luò)模型可用于研究區(qū)1、2、3與4周之后的地下水位預(yù)測(cè)。因此,將人工神經(jīng)網(wǎng)絡(luò)技術(shù)應(yīng)用于水文或水文地質(zhì)參數(shù)資料缺乏地區(qū)是可行的。
4 結(jié) 語(yǔ)
本文將3種神經(jīng)網(wǎng)絡(luò)算法模型用于研究區(qū)的地下水水位預(yù)報(bào)中,采用前饋神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)模擬了研究區(qū)6口觀測(cè)井1周后的地下水水位。網(wǎng)絡(luò)模型的輸入因子為此前1周蒸發(fā)量,水庫(kù)水位,排渠水位,抽水量和觀測(cè)井地下水位,共有15個(gè)輸入節(jié)點(diǎn)和6個(gè)輸出節(jié)點(diǎn)。使用4項(xiàng)統(tǒng)計(jì)指標(biāo)對(duì)3種網(wǎng)絡(luò)訓(xùn)練算法進(jìn)行評(píng)估。結(jié)果表明:3種訓(xùn)練算法產(chǎn)生的結(jié)果近似相同,可用這3種算法中的任意一種來(lái)對(duì)研究區(qū)的地下水水位預(yù)測(cè)。然而,根據(jù)本文的統(tǒng)計(jì)指標(biāo),BR算法略優(yōu)于其它2種算法。采用基于BR算法訓(xùn)練的人工神經(jīng)網(wǎng)絡(luò)模型進(jìn)一步對(duì)研究區(qū)未來(lái)2、3、4周的地下水水位進(jìn)行預(yù)測(cè)。結(jié)果發(fā)現(xiàn),隨著預(yù)測(cè)時(shí)間的推移,模型預(yù)測(cè)精度有降低的趨勢(shì),但是其精度仍然滿足實(shí)際需要,具有可信性。總體而言,盡管本研究中所使用的數(shù)據(jù)有限,但是經(jīng)過(guò)算法改進(jìn)的人工神經(jīng)網(wǎng)絡(luò)模型仍然能夠合理地預(yù)測(cè)研究區(qū)未來(lái)1周地下水位甚至更遠(yuǎn)時(shí)間(未來(lái)2、3、4周)的地下水水位。
[1] Todd DK, Mays LW. Groundwater hydrology[C].Wiley, Hoboken,2005.
[2] IWMI.The strategic plan for IWMI 2000-2005[M].International Water Management Institute(IWMI),Colombo,2005:28.
[3] Alley WM.The journey from safe yield to sustainability[J].Ground Water,2004, 42(1):12-16.
[4] 許國(guó)志.系統(tǒng)科學(xué)[M].上海:上海科技出版社,2003.
[5] 胡鐵松,袁鵬,丁晶.人工神經(jīng)網(wǎng)絡(luò)在水文水資源中的應(yīng)用[J].水科學(xué)進(jìn)展,1995,6(1):76-82.
[6] 張弘強(qiáng),王春紅.基于MATLAB的BP神經(jīng)網(wǎng)絡(luò)進(jìn)行教師評(píng)估[J].哈爾濱師范大學(xué)自然科學(xué)學(xué)報(bào),2005,21(5):43-46.
[7] 韓力群.人工神經(jīng)網(wǎng)絡(luò)理論、設(shè)計(jì)及應(yīng)用[M].北京:化學(xué)工業(yè)出版社,2002.
[8] 劉國(guó)東,丁晶.運(yùn)用BP網(wǎng)絡(luò)預(yù)測(cè)地下水位[J].西安地質(zhì)學(xué)院學(xué)報(bào),1997,19(2):52-57.
[9] ASCE Task Committee. Artificial neural networks in hydrology-II: hydrologic applications[J].J Hydrol Eng ASCE,2000, 5(2):124-137.
[10] Garcia LA, Shigdi A. Using neural networks for parameter estimation in ground water[J].J Hydrol,2006, 318(1-4):215-231.
[11] Samani M, Gohari-Moghadam M. A simple neural network model for the determination of aquifer parameters[J].J Hydrol,2007,340:1-11.
[12] Karahan H, Ayvaz MT.Simultaneous parameter identification of a heterogeneous aquifer system using artificial neural networks[J].Hydrogeol J,2008, 16:817-827.
[13] Hong YS, Rosen MR. Intelligent characterization and diagnosis of the groundwater quality in an urban fractured-rock aquifer using an artificial neural network[J].Urban Water,2001,3(3):193-204.
[14] Kuo V, Liu C. Evaluation of the ability of an artificial neural network model to assess the variation of groundwater quality in an area of black foot disease in Taiwan[J].Water Res,2004,38(1):148-158.
[15] Uddameri V.Using statistical and artificial neural network models to forecast potentiometric levels at a deep well in South Texas[J].Environ Geol,2007,51:885-895.
[16] Krishna B, Rao YRS, Vijaya T. Modeling groundwater levels in an urban coastal aquifer using artificial neural networks[J].Hydrol Process,2008, 22:1180-1188.
[17] Banerjee P, Prasad RK, Singh VS. Forecasting of groundwater level in hard rock region using artificial neural network[J].Environ Geol,2009, 58:1239-1246.
[18] 陳玉芳.BP神經(jīng)網(wǎng)絡(luò)的算法改進(jìn)及應(yīng)用研究[D].成都:電子科技大學(xué),2004.12-14.
[19] 楊旭,馮國(guó)章.基于BP網(wǎng)絡(luò)的中長(zhǎng)期水文預(yù)報(bào)精度影響分析[J].東北水利水電,2003,21(2):1-3.
[20] 邱林,陳曉楠.基于模擬退火算法的BP網(wǎng)絡(luò)在水文水資源中應(yīng)用[J].華北水利水電學(xué)院學(xué)報(bào),2005,26(1):123.
[21] 儲(chǔ)誠(chéng)山,張宏偉.基于遺傳算法和BP神經(jīng)網(wǎng)絡(luò)的用水量預(yù)測(cè)[J].中國(guó)農(nóng)村水利水電,2006,(4):36-38.
[22] Hagen MT, Demceth HB, Beale MN. Neural network design[M].PWS,Boston,1996.
[23] Bishop CM .Neural networks for pattern recognition[M].Oxford University Press,New York,1995.
[24] Mackay DJC.Apractical Bayesian framework for back-propagation networks[J].Neural Comput,1991,4(3):448-472.
[25] 張兵,袁壽其.基于L-M優(yōu)化算法的BP神經(jīng)網(wǎng)絡(luò)的作物需水量預(yù)測(cè)模型[J].農(nóng)業(yè)工程學(xué)報(bào),2004,20(6):73-76.
[26] Daliakopoulos IN, Coulibaly P.Groundwater level forecasting using artificial neural network[J].J Hydrol,2005,309:229-240.
[27] Bishop CM.Neural networks for pattern recognition[M].Oxford University Press, New York,1995.
[28] 魏鐵軍,王永成.BP網(wǎng)絡(luò)在三江平原井灌區(qū)地下水埋深預(yù)測(cè)中的應(yīng)用[J].黑龍江水專(zhuān)學(xué)報(bào),2009,36(1):26-30.
[29] 魏光輝. 基于RBF神經(jīng)網(wǎng)絡(luò)的河川年徑流量預(yù)測(cè)[J].西北水電,2014,(05):14-17.
[30] 鄧麗娟. 新疆車(chē)爾臣河流域近50余年來(lái)主要水文要素變化研究[D].烏魯木齊:新疆農(nóng)業(yè)大學(xué),2012.
Dynamic Variation Simulation of Ground Water Table Based on Artificial Neural Network Model
WEI Guang-hui
(College of Hydraulic and Civil Engineering, Xinjiang Agricultural University, Urumqi 830052,China)
Predication of the ground water table plays an important role in planning management of catchement surface and ground water resources. In this study, the artificial neural network model is applied in predication of the ground water table around the Xinier reservoir. By application of data from 6 monitoring wells in the study area and of the artificial neural network model, the ground water table after one week is predicated by simulation. The factors input the model include evaporation, reservoir level, escape canal level, water pumped volume and ground water table of the monitoring wells in last week. Therefore, the model is with 15 input points and 6 output points. Three different neural network methods of GDX, LM and BR methods are applied for the predication of the ground water table. The study shows that all three methods perform well in the predication. Generally, BR performance is better than these of GDX and LM. The artificial neural network model trained by BR method is applied for the predication of the ground water table in future 2nd, 3rd and 4th weeks in the study area. The simulation results are still better although the accuracy of the predication of the ground water table slightly decreases with time increment.
artificial neural network model; predication of ground water table; GDX method; LM method; BR method
2014-12-21
魏光輝(1981- ),男,新疆石河子人,高級(jí)工程師,主要從事干旱區(qū)水資源利用與工程建設(shè)管理.
新疆水文學(xué)及水資源重點(diǎn)學(xué)科資助(XJSWSZYZDXK2010-12-02).
P641.2
A
10.3969/j.issn.1006-2610.2015.03.002

