大口徑反射鏡輕量化及其支撐結構設計

李 暢，何 欣

(1.中國科學院長春光學精密機械與物理研究所，長春130033;2.中國科學院大學，北京100049)

引 言

隨著科學技術的不斷發展以及對地觀測要求的不斷提高，高分辨率、寬覆蓋的空間相機逐漸成為光學遙感器的發展趨勢，因此，通常采用具有長焦距、大口徑、大視場等特點的離軸三反光學系統［1-2］。大口徑反射鏡作為光學系統中的一個關鍵元件，在其制造裝配、地面試驗、運載發射以及在軌工作等過程中，會受到重力、溫度變化以及振動等各種復雜環境因素的影響，而這些復雜的環境因素容易使其面形和位置(剛體位移和轉角)發生變化，導致空間相機光學系統的光軸指向產生偏離、波像差變大，進而致使相機的分辨率下降、光學性能變壞。因此，如何設計精度較高的反射鏡及其支撐結構，以減弱或消除上述各種環境因素變化對相機光學系統的影響，始終是國內外科研人員在空間相機研制過程中的重要研究內容和方向［3-4］。

基于此，本文中對某超寬覆蓋空間相機的主反射鏡進行了設計研究，其外形尺寸為800mm×400mm，采用SiC材料制造，屬于大口徑反射鏡。為了完成高比剛度的反射鏡設計，且滿足光學成像要求，作者主要在反射鏡支撐方式選擇、支撐結構設計及鏡體輕量化等方面進行了分析優化，并利用環境試驗進行了上述組件結構的穩定性測試。

1 支撐結構設計

1．1 支撐方式和支撐點選擇

由于相機采用全反射光學系統，反射鏡的背部不參與光束傳輸，因此，常采用剛度較高的背部支撐方式［5］。

對于背部支撐方式，設鏡面在重力下變形量為δ，有如下經驗公式［6］:式中，δ為能接收的鏡面變形峰谷(peak valley，PV)值，通常PV值取波長的1/10，ρ為材料的密度，g為重力加速度，r表示反射鏡半徑(長條形反射鏡即為對角線長度的一半，下同)，E為材料的彈性模量，t代表反射鏡厚度。由(1)式即可得到主鏡的厚度t=93mm。

支撐點數量對反射鏡鏡面變形影響較大，定義最少支撐點數為N，有如下規律［7］:

將主鏡各參量代入(2)式中，可推算出N=3.4。由于上述經驗公式計算的結果未考慮反射鏡鏡體的輕量化，且根據反射鏡半運動學安裝原理中支撐點分布、自由度約束以及結構支撐的穩定性等因素，若選用4點支撐方式，必須采用多層支撐形式以滿足自由度約束要求，造成支撐結構剛度低、質量大、裝配難度高等缺點，因此，本文中選用背部3點支撐方式，以滿足主鏡對支撐結構尺寸、質量和自由度的要求。

對于主鏡背部3個支撐點，其分度圓半徑R用以下方法確定［8］:

由于主鏡為長條形反射鏡，在寬度方向上，支撐點應盡量靠近兩邊，提高寬度方向的剛度，在長度方向上，取兩支撐點間距S =。

1．2 柔性支撐結構設計

在主鏡支撐結構上減弱了個別方向上的剛度，引入了一定的柔性，以此來抵消反射鏡由于溫度變化產生的熱應力和微小變形。柔性鉸鏈被廣泛應用于支撐結構的柔性設計領域，其具有無機械摩擦、結構簡單、釋放自由度和靈敏度高等特點［9］。

柔性鉸鏈通過在某一方向上切開一個柔性槽，以降低該方向上的剛度，體現其柔性，使其能夠產生微小變形，釋放熱應力，只存在一個柔性槽的柔性鉸鏈被稱為單向柔性鉸鏈，而在一般情況下，往往將多個柔性槽成組使用，即可實現在多方向上的柔性，達到釋放多個自由度的目的，將其稱之為多層柔性鉸鏈。

由于主鏡采用背部3點支撐方式，在反射鏡長度方向上對稱分布支撐點位置，基于半運動學安裝定位原理，每個柔性支撐結構需要約束兩個方向的自由度，因此，采用3層組合式柔性鉸鏈，釋放4個方向的自由度，參考Bipod雙腳架設計原理，設計如圖1所示柔性支撐結構，其分為兩個部分，上部分與反射鏡支撐孔粘接，下部分與支撐背板連接，上下兩部分通過螺釘連接。3個柔性鉸鏈對心安裝，便可以恰好約束鏡體6個方向的自由度，又不會因為過定位產生裝配應力。支撐背板的作用是固定連接3個柔性支撐結構，將反射鏡固定安裝在框架指定位置，因此采用高強度的加強筋與薄壁組合的結構形式，組成多個結構封閉的四邊形單元，以達到支撐背板高剛度的的要求。

Fig.1 Flexible supporting structure

對比材料各項性能指標，綜合考慮力學性能、熱性能、對空間環境的適應性以及加工工藝性等因素，選用線脹系數經過特殊匹配的Invar作為反射鏡柔性支撐結構的材料，采用比剛度高、導熱性好、線脹系數低的高體份SiC/Al復合材料作為支撐背板的材料。

根據上述支撐方式和支撐結構的設計結果，主鏡支撐結構如圖2所示。

Fig.2 Sketch of support structure for primary mirror

2 鏡體輕量化設計

在反射鏡背部，布置一系列形狀規則的三角形輕量化孔，具有輕量化率較高、剛度好、“網格效應”低、加工制造工藝成熟等優點［10］。

根據背部3點支撐形式，建立反射鏡鏡體初始結構模型如圖3所示，其中各結構尺寸參量的初值為:支撐孔直徑D=88mm，支撐孔壁厚td=20mm，輕量化孔直徑d=16mm，鏡體厚度 H=93mm，切角 α=40°，鏡面厚tf=8mm，外壁厚ta=8mm，加強筋厚tb=8mm。

Fig.3 Initial structure model of mirror

為確定主鏡鏡體最優的結構尺寸，在反射鏡剛度最大和質量最小之間取得最佳平衡，需要對鏡體進行優化設計。首先建立反射鏡的有限元模型，分析其在1g重力作用下的變形，并提取鏡面最大變形結果，生成優化過程中所需要的分析文件，然后，選擇優化處理器，確定目標函數為反射鏡質量最小，狀態變量為1g重力作用下的鏡面最大變形結果，設計變量為反射鏡結構尺寸參量，選擇背部3點支撐約束，指定優化方法及循環控制方式，便可以進行優化分析。

但是，在主鏡結構優化設計過程中，影響反射鏡鏡體質量和剛度的結構參量有很多，若都進行優化設計，會使設計變量增多，迭代次數增加，運算效率降低，甚至導致無法收斂。由于各結構尺寸的影響程度各不相同，可以首先分析各參量對鏡體質量和1g重力條件下鏡面最大變形量的影響，如圖4和圖5所示。因此，在進行結構優化分析之前，先確定影響較小的結構尺寸參量，降低計算規模，再對影響較大的結構尺寸參量進行多變量優化。

Fig.4 Relationship between structure size and mirror quality

Fig.5 Relationship between structure size and the maximum deformation of mirror

由圖4可以看出，鏡體厚度H、鏡面厚tf、加強筋厚tb和外壁厚ta這4條曲線斜率較大，隨著各結構尺寸的增加，鏡體質量m顯著增大，而其它參量變化對鏡體質量基本沒有影響。同樣，從圖5中可以看到，鏡體厚度H，鏡面厚tf和支撐孔徑D這3條曲線的斜率較大，對1g重力條件下鏡面的法向最大變形量Dmax影響較大。

綜合比較，本文中將鏡體厚度H、支撐孔徑D、鏡面厚tf、外壁厚ta、加強筋厚tb這5個結構尺寸參量作為設計變量，鏡體質量m作為優化分析的目標函數，1g重力條件下鏡面的法向最大變形量Dmax作為狀態變量進行多參量優化，其它結構尺寸仍采用初始值不變，優化迭代過程如圖6所示。

Fig.6 Relationship between structure parameters and iteration number

根據各結構尺寸參量最終取值，建立反射鏡鏡體模型，如圖7所示，SiC反射鏡鏡體的質量為18.54kg，與相同尺寸的實心鏡坯相比，輕量化率高達80.5%，在1g重力條件下，反射鏡鏡面的法向最大變形量為5.23μm。

Fig.7 The final structure model of mirror

3 反射鏡組件有限元分析

對經過分析和優化設計后的主鏡組件進行有限元分析，在建立結構的有限元模型時，以六面體Hex6單元為主，以提高分析精度和效率。利用有限元分析軟件，分析得到主鏡組件在重力和溫度影響下的變化結果，見表1和表2，模態分析得到1階頻率如圖8所示。

Table 1 Influence of gravity on primary mirror

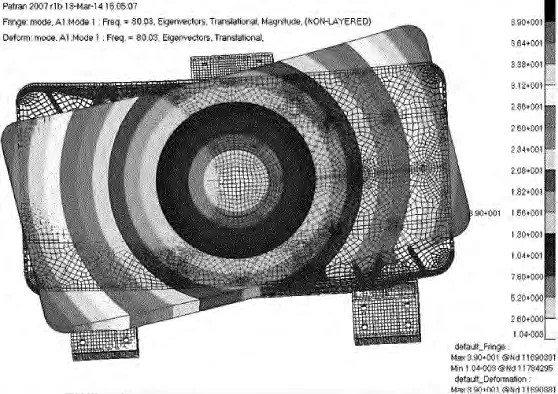
Fig.8 The first-order frequency of primary mirror

由分析結果可以看出，主鏡組件在重力和溫度變化作用下，表征面形變化的PV值和均方根(root mean square，RMS)值，以及表征位置變化的位移值和轉角值均能滿足設計要求，1階頻率為80.03Hz，滿足衛星對載荷特征頻率大于60Hz的要求，因此，主鏡組件結構具有較好的力學適應性、溫度適應性和動態剛度。

4 力學振動試驗

Fig.9 Vibration test of primary mirror

為了驗證上述有限元分析結果的正確性，以及對實際加工裝配后的主鏡組件結構的穩定性有一個客觀評價，對主鏡進行了1g正弦掃頻試驗，測試結構的實際模態，如圖9所示。振動響應曲線如圖10所示，縱坐標表示對測點加速度響應值Ma求以10為底的對數。從響應曲線可以看出，主鏡組件的實際1階頻率為73.06Hz，動態剛度較高，且與有限元分析誤差不到10%，說明了有限元分析結果精度較高。

Fig.10 Response curve of 1g sinusoidal vibration

5 結論

結合自由度理論和柔性鉸鏈原理，完成了主鏡支撐方式和柔性支撐結構的設計，利用參量化建模方法，完成了鏡體的輕量化設計與優化。最后，進行了相應的有限元分析，分析結果顯示，組件具有較好的力學和熱學性能，1階頻率較高，說明主鏡組件鏡體輕量化及柔性支撐結構設計合理，滿足設計要求。

［1］ XIONG Z，YUAN X D，LIU Q G，et al.ANYSYS finite element analysis and experiment study of large aperture reflectors［J］.Laser Technology，2009，33(1):107-109(in Chinese).

［2］ XU T Z，XIN H W，HE X.Random vibration fatigue analysis for mirror component of space camera ［J］.Optical Technique，2013，39(6):549-552(in Chinese).

［3］ AHMAD A.Handbook of optomachanical engineering［M］.Boca Raton，USA:CRC Press，1997:298.

［4］ LI C，HE X.Design and optimization of trussed structure for space camera based on Rayleigh algorithm［J］.Infrared and Laser Engineering，2012，41(9):2405-2409(in Chinese).

［5］ ZHANG X J，LI Z L，ZHANG Z Y.Space telecope aspherical mirror structure design based on SiC material［J］.Infrared and Laser Engineering，2007，36(5):577-582(in Chinese).

［6］ WANG Y，ZHANG J X.Optimization and analysis for the support of the large aperture telescope primary mirror［J］.Opto-Electronic Engineering，2009，36(1):107-113(in Chinese).

［7］ FAN Y C，CHAI F M.Support design for primary mirror with large aperture of optical remote sensor［J］.OME Information，2010，27(5):16-21(in Chinese).

［8］ YODER P R.Opto-mechanical system design［M］.2nd ed.New York，USA:Marcel Dekker，1993:376.

［9］ BAO H，LI Z L.Design of the strip SiC mirror supporting structure and lightweight［J］.Optical Technique，2008，34(4):593-596(in Chinese).

［10］ HAN Y Y，ZHANG Y M，HAN J C，et al.Optimum design of lightweight silicon carbide mirror［J］.Opto-Electronic Engineering，2006，33(8):123-135(in Chinese).