格蘭-付科棱鏡光強(qiáng)透射比曲線(xiàn)波動(dòng)成因的研究

徐兆鵬，朱化鳳，劉 鑫，王天陽(yáng)，劉 佩，李 超

(中國(guó)石油大學(xué)(華東)理學(xué)院，青島266580)

引 言

隨著光學(xué)技術(shù)的發(fā)展，偏振器件在科學(xué)研究和實(shí)際應(yīng)用中起著越來(lái)越重要的作用。由于冰洲石具有光學(xué)性能穩(wěn)定、透射光譜范圍寬(240nm～2800nm)、雙折射率大、具有極好的抗光損傷能力等優(yōu)點(diǎn)［1-3］，因此，當(dāng)前所用的偏光器件有相當(dāng)一部分是利用天然冰洲石晶體制作而成。在許多情況下偏振器都是成對(duì)使用，一個(gè)充當(dāng)起偏器，一個(gè)充當(dāng)檢偏器。理論上，一束線(xiàn)偏振光在通過(guò)起偏器后，其光強(qiáng)透射比會(huì)隨著檢偏器(格蘭-付科棱鏡)的旋轉(zhuǎn)滿(mǎn)足馬呂斯定律曲線(xiàn)。然而實(shí)際研究表明，隨著檢偏器的旋轉(zhuǎn)，曲線(xiàn)不會(huì)完全服從馬呂斯定律曲線(xiàn)，而是光強(qiáng)透射比隨著入射角、入射波長(zhǎng)等的變化，在馬呂斯定律曲線(xiàn)的基礎(chǔ)上，產(chǎn)生一些上下的周期性波動(dòng)［4］。這種波動(dòng)對(duì)格蘭-付科棱鏡表現(xiàn)得尤為明顯。這一現(xiàn)象會(huì)給實(shí)際應(yīng)用，特別是在一些檢偏器需要調(diào)整的環(huán)境下帶來(lái)不利影響［5-6］。格蘭-付科棱鏡是偏振器件的一種，是由兩塊光軸平行于入射面而垂直于三角平面的兩塊三角形的冰洲石晶體膠合在一起構(gòu)成的［7-9］，它在激光技術(shù)中被廣泛應(yīng)用［10-12］。

目前來(lái)看，偏光棱鏡光強(qiáng)透射比波動(dòng)產(chǎn)生的原因相關(guān)方面的研究只有定性的結(jié)果和解釋?zhuān)?，9］，提出光強(qiáng)透射比波動(dòng)與空氣隙間光的干涉有關(guān)，但理論與實(shí)驗(yàn)結(jié)果還相差較大。有學(xué)者進(jìn)行了格蘭-付科棱鏡空氣隙厚度的測(cè)量，考慮了光在空氣隙間的干涉，分析了棱鏡對(duì)單模高斯光束的影響，認(rèn)為透射光束隨光束在棱鏡端面上的入射角變化呈現(xiàn)周期性震蕩，且震蕩特性與入射光的波長(zhǎng)、光強(qiáng)分布特性、棱鏡結(jié)構(gòu)角及空氣隙的厚度有關(guān)［5，13］。

作者利用偏振光實(shí)驗(yàn)系統(tǒng)對(duì)格蘭-付科棱鏡的光強(qiáng)透射比進(jìn)行了實(shí)驗(yàn)，并且通過(guò)設(shè)定棱鏡參量利用光的干涉原理對(duì)實(shí)驗(yàn)過(guò)程進(jìn)行數(shù)值模擬，把得到的數(shù)值模擬結(jié)果和實(shí)驗(yàn)結(jié)果比較分析，結(jié)果二者符合得非常好。

1 格蘭-付科棱鏡的光學(xué)透射特性實(shí)驗(yàn)

1．1 實(shí)驗(yàn)裝置圖

如圖1所示，一束激光出射后穿過(guò)起偏器后變成線(xiàn)偏振光，然后通過(guò)固定在高精度步進(jìn)電機(jī)上的檢偏器(由格蘭-付科棱鏡充當(dāng))，再用光電探測(cè)器收光強(qiáng)信息，用信息控制與處理系統(tǒng)對(duì)光強(qiáng)進(jìn)行處理。為了便于比較，調(diào)整初始狀態(tài)為起偏器與檢偏器的偏振方向垂直。這樣便可方便地比較透射光強(qiáng)隨旋轉(zhuǎn)角的變化關(guān)系曲線(xiàn)。

Fig.1 Schematic of optical path

1．2 實(shí)驗(yàn)結(jié)果

實(shí)驗(yàn)表明，對(duì)同一格蘭-付科棱鏡進(jìn)行多次實(shí)驗(yàn)，其光強(qiáng)透射比曲線(xiàn)的形狀有多種形式。當(dāng)所用格蘭-付科棱鏡的空氣隙的厚度約為20μm、入射波長(zhǎng)為632.8nm時(shí)，圖2中給出了一些實(shí)驗(yàn)中所得的棱鏡在一個(gè)旋轉(zhuǎn)周期內(nèi)的幾條典型光強(qiáng)透射比曲線(xiàn)。從這些曲線(xiàn)可以看出，格蘭-付科棱鏡的光強(qiáng)透射比曲線(xiàn)在馬呂斯定律所給出的曲線(xiàn)的基礎(chǔ)上出現(xiàn)了一些明顯的波動(dòng)。

Fig.2 Typical transmittance curve with the rotation of prism

2 光強(qiáng)透射比公式

當(dāng)一束光入射到格蘭-付科棱鏡的時(shí)候，大部分光直接透射，由于棱鏡的膠合面光潔度非常高，部分光在空氣隙間要發(fā)生多光束干涉。

格蘭-付科棱鏡的結(jié)構(gòu)如圖3所示。n2和n′的反方向代表入射光和折射光的波矢方向，n1是入射端面的法線(xiàn)方向，n2是剖面的法線(xiàn)方向。由n1和n2確定的平面為棱鏡主截面。n1和n2之間的夾角等于結(jié)構(gòu)角S。中間帶點(diǎn)的圓圈代表晶體的光軸。下面提到的軸線(xiàn)指的是從交點(diǎn)O開(kāi)始、方向向上的射線(xiàn)。

Fig.3 Illustration model for Glan-Foucault prism experiments

為表示檢偏器在圖1中所示的實(shí)驗(yàn)裝置中的空間位置，假設(shè)檢偏器的在步進(jìn)電機(jī)上的旋轉(zhuǎn)軸為n0′，以n1為軸線(xiàn)，俯視逆時(shí)針?lè)较驈闹鹘孛娴饺肷涿嬷g轉(zhuǎn)過(guò)的角度為Ψ，為入射光的方位角。入射角j和方位角Ψ的組合被稱(chēng)為空間入射角。旋轉(zhuǎn)軸n0′和出射面的法線(xiàn)n1間的夾角為α;入射光的法線(xiàn)n′和旋轉(zhuǎn)軸n0′間的夾角為 β;平面 n0′-n2繞 n0′逆時(shí)針旋轉(zhuǎn)到面n0′-n′所轉(zhuǎn)過(guò)的角度為 Φ′，檢偏器的旋轉(zhuǎn)角 Φ =Φ′-Φ0，其中Φ0是Φ′的初始值。角度Ψ，α，β，Φ 和Φ0共同決定了隨著檢偏器轉(zhuǎn)動(dòng)時(shí)的空間入射角。

根據(jù)幾何關(guān)系，隨著空間入射角以及轉(zhuǎn)軸方位的不同，光束在空氣隙上的入射角就不同。設(shè)光束在空氣隙上的折射角和入射角分別為i和j，如圖4所示。光束在空氣隙表面的光強(qiáng)反射比R符合菲涅耳公式s分量的表達(dá)式，可表示為:

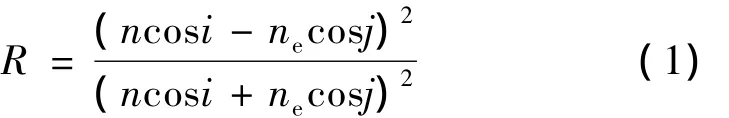
式中，n為空氣折射率，ne為晶體中e光的折射率。

考慮到多光束干涉的影響，當(dāng)從起偏器出射的線(xiàn)偏振光入射到格蘭-付科棱鏡，隨著檢偏器的轉(zhuǎn)動(dòng)光強(qiáng)透射比可表示為［13］:

Fig.4 Structure of air gap

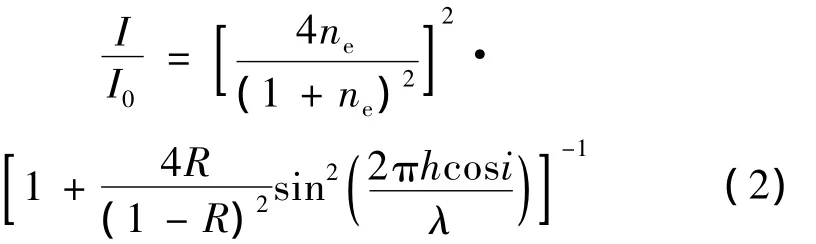
式中，h為空氣隙厚度，λ為入射光波長(zhǎng)，I為透射光強(qiáng)，I0為入射光強(qiáng)。

3 數(shù)值模擬實(shí)驗(yàn)

結(jié)合上面的實(shí)驗(yàn)參量，格蘭-付科棱鏡空氣隙厚度h=20μm，He-Ne激光器的出射波長(zhǎng)為632.8nm，棱鏡結(jié)構(gòu)角取S=38.8528°，晶體中 e光主折射率 ne=1.48515。一個(gè)棱鏡的空氣隙、結(jié)構(gòu)角等量是固定不變的，因此通過(guò)改變?chǔ)罚粒拢?的值可以得到不同數(shù)值模擬曲線(xiàn)。利用MATLAB可以模擬出這些角度取不同值條件下的光強(qiáng)透射比曲線(xiàn)(如圖5所示)。

Fig.5 Simulated graph in different initial conditions

圖5 中曲線(xiàn) a、曲線(xiàn) b、曲線(xiàn) c分別為當(dāng) Ψ =0°，α =0．06°，β =0．76°，Φ0=10°;Ψ =0．5°，α =0．3°，β =1．6°，Φ0=8°;Ψ =0．4°，α =0．4°，β =1°，Φ0=15°時(shí)所對(duì)應(yīng)的曲線(xiàn)，它們分別可與圖2中的曲線(xiàn)a、曲線(xiàn)b、曲線(xiàn)c 3條線(xiàn)對(duì)應(yīng)。

比較圖5和圖2可知，數(shù)值模擬的結(jié)果與實(shí)驗(yàn)結(jié)果相一致，有所差別的地方主要來(lái)源于棱鏡經(jīng)過(guò)膠合之后，空氣隙的厚度很難與理論設(shè)計(jì)相一致，會(huì)在一定程度上影響干涉的強(qiáng)弱，致使模擬曲線(xiàn)和實(shí)驗(yàn)曲線(xiàn)略有差別。圖中只是給出了部分理論模擬和實(shí)驗(yàn)結(jié)果，其它大量的實(shí)驗(yàn)曲線(xiàn)都可以找到其對(duì)應(yīng)的理論模擬結(jié)果，只是對(duì)應(yīng)的初始角度有所不同。實(shí)驗(yàn)中所得曲線(xiàn)的光強(qiáng)透射比值整體上較數(shù)值模擬所得值偏小，這是由于實(shí)際的實(shí)驗(yàn)中除了存在反射損失外，還存在其它形式的光能損失，如散射存在光能量損失等。

4 討論

從圖5與圖2的比較結(jié)果也可以看出，數(shù)值模擬圖和實(shí)驗(yàn)圖在透射比峰值對(duì)應(yīng)轉(zhuǎn)角以及曲線(xiàn)形狀等方面還存在一定差異。針對(duì)此差異，分析其主要來(lái)源是在對(duì)實(shí)驗(yàn)進(jìn)行模擬的過(guò)程中所取的各個(gè)參量不一定跟實(shí)驗(yàn)過(guò)程中的實(shí)際參量完全一致，而且有些參量取值的微小變化都會(huì)對(duì)曲線(xiàn)有一定的影響。舉例說(shuō)明如下。首先討論在Ψ，α，β，Φ0的值相同的條件下，改變空氣隙厚度h、棱鏡結(jié)構(gòu)角S以及入射光波長(zhǎng)λ時(shí)所得到的圖像的形狀。為了使模擬結(jié)果便于分析，采用控制變量法進(jìn)行數(shù)值模擬，取 Ψ =0°，α=0．06°，β =0．76°，Φ0=10°保持不變，依次改變空氣隙厚度 h、棱鏡結(jié)構(gòu)角S以及入射光波長(zhǎng)λ得到數(shù)值模擬圖。圖5中曲線(xiàn)a為對(duì)照組模擬圖線(xiàn)，參量為h=20μm，S=38.8528°，λ =632.8nm。曲線(xiàn) b、曲線(xiàn) c、曲線(xiàn) d 為實(shí)驗(yàn)組模擬圖線(xiàn)，參量分別為h=21μm，S=38.8528°，λ =632.8nm;h=20μm，S=38.8°，λ =632.8nm;h=20μm，S=38.8528°，λ =631nm。

從圖6中的曲線(xiàn)a、曲線(xiàn)b、曲線(xiàn)c和曲線(xiàn)d可以看出，在Ψ，α，β，Φ0保持不變的條件下，通過(guò)微小改變棱鏡空氣隙厚度h、棱鏡結(jié)構(gòu)角S以及晶體入射光波長(zhǎng)λ中的任何一個(gè)值都會(huì)使曲線(xiàn)的峰值與形狀發(fā)生一定的變化，這說(shuō)明微小的角度、厚度、入射波長(zhǎng)等的變化都會(huì)使實(shí)驗(yàn)?zāi)M圖像與對(duì)照模擬圖像有角度上和形狀上的不對(duì)應(yīng)。而在實(shí)驗(yàn)中，想要得到準(zhǔn)確的棱鏡空氣隙厚度h、棱鏡結(jié)構(gòu)角S的值以及單一波長(zhǎng)的入射光是不容易的，總會(huì)存在一定誤差，要模擬出完全相同的曲線(xiàn)非常困難。除此之外，任何其它的角度參量Ψ，α，β，Φ0的微小變化也都會(huì)產(chǎn)生曲線(xiàn)的微小平移或形變。因此，在本文中的數(shù)值模擬與實(shí)驗(yàn)結(jié)果的對(duì)比中，只考慮曲線(xiàn)的大體形狀與峰值個(gè)數(shù)等主要特征而忽略其諸如峰值對(duì)應(yīng)轉(zhuǎn)角的細(xì)節(jié)。

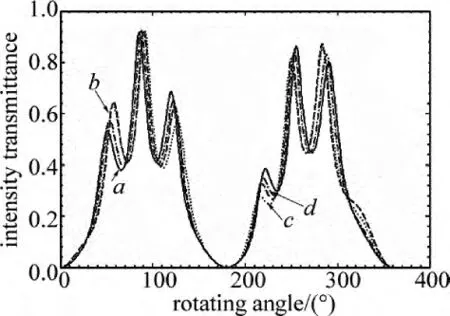
Fig.6 Simulated graph of controlled experiment with slight varing of h，S，λ

模擬實(shí)驗(yàn)中，同一參量比較大的變化會(huì)使曲線(xiàn)產(chǎn)生比較大的形變。例如格蘭-付科棱鏡空氣隙厚度在膠合過(guò)程中會(huì)與預(yù)設(shè)的值有差別。根據(jù)(1)式和(2)式，h的變化會(huì)影響干涉條件，從而影響光強(qiáng)透射比曲線(xiàn)的波動(dòng)。在實(shí)際研究與應(yīng)用中，一般在膠合過(guò)程中，(1)式和(2)式中的空氣隙厚度h不能取為0(甚至接近于0)，否則就將產(chǎn)生倏逝波;h也不能太大，否則空氣隙的直接透射光束和反射之后透射的光束之間的光程差超出了相干長(zhǎng)度，將無(wú)法發(fā)生干涉，要討論厚度的影響，可以在15μm～35μm范圍內(nèi)討論。圖7中曲線(xiàn)a、曲線(xiàn) b、曲線(xiàn) c為當(dāng)參量 Ψ =0°，β =0．1°，α =0．4°，Φ0=15°，h 分別為 15μm，25μm，30μm 時(shí)根據(jù)(2)式所得的數(shù)值模擬曲線(xiàn)。

Fig.7 Simulated intensity transmittance curve of the prism with the same initial angle for different thickness of air gap

從圖7中可以看出，格蘭-付科棱鏡在一個(gè)旋轉(zhuǎn)周期內(nèi)，隨著空氣隙厚度h的增大，光通過(guò)棱鏡后的光強(qiáng)透射比曲線(xiàn)上會(huì)出現(xiàn)數(shù)量越來(lái)越多的波動(dòng)。從這個(gè)角度出發(fā)，可以考慮通過(guò)控制格蘭-付科棱鏡空氣隙的厚度的方法來(lái)適當(dāng)減少格蘭-付科棱鏡光強(qiáng)透射比曲線(xiàn)的波動(dòng)。

5 曲線(xiàn)上波動(dòng)的抑制

根據(jù)以上棱鏡的透射比曲線(xiàn)上的波動(dòng)的成因，有兩種方法可抑制曲線(xiàn)上的波動(dòng)。

方法一:根據(jù)馬呂斯定律的修正公式［14］:

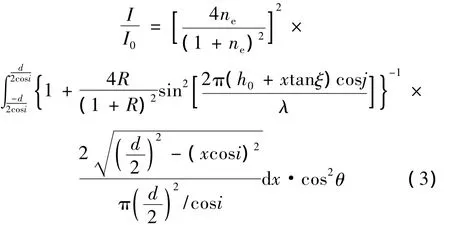
式中，ξ為空氣隙的膠合誤差，x為光斑的某部分在空氣隙上相對(duì)于中心的坐標(biāo)位置，d為入射光束的光斑直徑，h0為棱鏡空氣隙厚度。取不同的空氣隙的膠合誤差進(jìn)行數(shù)值模擬。圖8中a，b，c 3條曲線(xiàn)所示分別對(duì)應(yīng)的參量分別為 α =0．06°，β =0．76°，Φ0=10°，ξ=0．1°;α =0．06°，β =0．76°，Φ0=10°，ξ=0．2°，Ψ =0°，α =0．06°，β =0．76，Φ0=10°，ξ=0．3°。圖8 中3 條曲線(xiàn)參量與圖5中曲線(xiàn)a參量相比，不同之處只有圖5中曲線(xiàn)a的空氣隙的膠合誤差 ξ=0°。

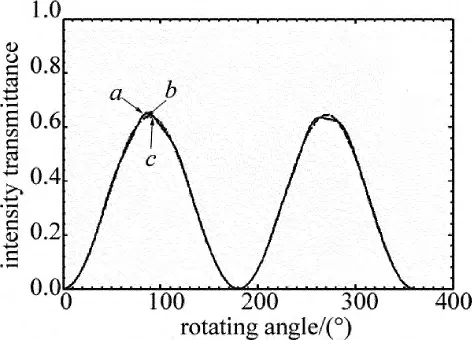
Fig.8 Simulated graph of modified formulas of the Malus law

由圖8可見(jiàn)，格蘭-付科棱鏡的光強(qiáng)透射比曲線(xiàn)波動(dòng)曲線(xiàn)的波動(dòng)可以通過(guò)在棱鏡膠合的過(guò)程中給定一個(gè)合適的誤差得以抑制。

方法二:令圖3中入射光的法線(xiàn)n′和旋轉(zhuǎn)軸n0′間的夾角β=0°，可以實(shí)現(xiàn)光強(qiáng)透射比曲線(xiàn)上波動(dòng)的完全抑制。圖9中3條曲線(xiàn)為圖5中3條曲線(xiàn)在β=0°且其余參量均相同的情況下的數(shù)值模擬圖，兩圖中a，b，c 3條曲線(xiàn)依次對(duì)應(yīng)。從圖9和圖5的比較結(jié)果可以看出，令β=0°可以有效抑制格蘭-付科棱鏡光強(qiáng)透射比曲線(xiàn)上的波動(dòng)。

Fig.9 Simulated graph when β =0°

6 結(jié)論

通過(guò)實(shí)驗(yàn)測(cè)量了格蘭-付科棱鏡的光強(qiáng)透射比，對(duì)可能出現(xiàn)的情況進(jìn)行了數(shù)值模擬，模擬結(jié)果與實(shí)驗(yàn)結(jié)果相一致，證實(shí)了格蘭-付科棱鏡光強(qiáng)透射比曲線(xiàn)上的波動(dòng)產(chǎn)生的具體原因，即是由于光束的空間入射角的不同致使其在膠合面上的入射角變化，進(jìn)而引起光束在空氣隙間多光束干涉條件的變化所產(chǎn)生的，這為設(shè)計(jì)出能抑制光強(qiáng)透射比曲線(xiàn)波動(dòng)的格蘭-付科棱鏡提供了一種思路。根據(jù)透射比曲線(xiàn)上波動(dòng)的成因，提出了抑制光強(qiáng)透射比波動(dòng)的方法兩種方法，令棱鏡的轉(zhuǎn)軸和系統(tǒng)的光軸重合或給棱鏡設(shè)定一個(gè)合適的膠合誤差，兩種方法均可有效地抑制光強(qiáng)透射比曲線(xiàn)的波動(dòng)。

［1］ WANG T，WU F Q，MA L L.Effect of air-gap polarizing prism on distribution of light intensity of single-mode gaussian beam［J］.Acta Optica Sinica，2006，26(9):1335-1339(in Chinese).

［2］ ZUBOV V A.Polarization analyzes operating in a wide spectral range［J］.Journal of Russian Laser Research，1997，18(1):17-38.

［3］ WANG T，WU F Q，MA L L.Transmitting characteristics of deferent girding radios single mode Gaussian beam［J］.Journal of Qufu Normal University(Nature Science Edition)，2006，32(4):72-74(in Chinese).

［4］ LI H X，F(xiàn)AN J Y，SU F F，et al.Suppressing the disturbance in the transmission of Glan-Thompson-type prism polarizers［J］.Chinese Optics Letters，2010，8(4):428-430.

［5］ MENG X Sh，WANG T，WU F Q，et al.The measurement of the Glan-Foucault prisms air-gap. ［M］.Laser Technology，2010，34(3):413-416(in Chinese).

［6］ ZHU H F，SONG L K，CHEN J W，et al.Modified formula of Malus’law for Glan-Taylor polarizing prisms［J］.Optics Communication，2004，245(1/6):1-9.

［7］ FAN J Y，LI H X，WU F Q.A study on transmitted intensity of disturbance for air-spaced Glan-type polarizing prisms［J］.Optics Communication，2003，223(1):11-16.

［8］ LI H X，WU F Q，F(xiàn)AN J Y.Thermodynamic effect on transmitted intensity perturbance of air-gaped Glan-type polarizing prisms［J］.Acta Physica Sinica，2003，52(8):2081-2085(in Chinese).

［9］ WANG C M，SONG L K，WANG L，et al.Effect of incident angles on splitting ratio of Glan polarizing splitting prisms［J］.Laser Technology，2008，32(2):102-104(in Chinese).

［10］ LI J Zh，LI G H.Spectrophotometer polarization spectrum measurement［J］.Spectroscopy and Spectral Analysis，1994，14(5):121-126.

［11］ LI J Zh.Handbook of optics［M］.Xi’an:Technology and Science Press of Shanxi，1986:497-521(in Chinese).

［12］ BENNETT J M.Handbookofoptics［M］.NewYork，USA:McGraw-Hill，1995:3.1-3.19.

［13］ ZHU J K，WU F Q，REN Sh F.Forward and backward splitting angles of Wollaston prisms and their symmetry［J］.Laser Technology，2012，36(5):636-638(in Chinese).

［14］ ZHU H F，LI D L，SONG L K，et al.Precise analysis of formation and suppression of intensity transmittance fluctuations of glan-taylor prisms［J］.Laser ＆ Optoelectronics Progress，2013(5):052302(in Chinese).