隨機(jī)變量非正態(tài)分布且相關(guān)的機(jī)械零件單模失效可靠度分析

劉華漢，蔣 瑋，楊光輝，呂海霆

（大連理工大學(xué) 機(jī)械工程學(xué)院，遼寧 大連 116024）

0 引 言

機(jī)械產(chǎn)品的可靠性設(shè)計(jì)不同于電子產(chǎn)品可靠性設(shè)計(jì).對(duì)機(jī)械系統(tǒng)來(lái)說(shuō)有3種不同形式的相關(guān)性問(wèn)題：一是考慮引起零件單模失效的隨機(jī)變量相關(guān)性問(wèn)題，二是考慮零件失效模式之間相關(guān)性問(wèn)題，三是機(jī)械系統(tǒng)零件間的相關(guān)性問(wèn)題.而對(duì)于機(jī)械系統(tǒng)中單個(gè)零件的可靠度分析，應(yīng)充分考慮上述前兩種相關(guān)性問(wèn)題.目前的研究工作集中在零件失效模式間相關(guān)性問(wèn)題及機(jī)械零件（單模失效）間的相關(guān)性問(wèn)題［1－10］的研究方面，而對(duì)于機(jī)械零件隨機(jī)變量相關(guān)的單模失效問(wèn)題的研究鮮有報(bào)道.

機(jī)械零件可靠度計(jì)算的基本理論為應(yīng)力－強(qiáng)度干涉理論（又稱(chēng)為應(yīng)力－強(qiáng)度相干模型），在以往的文獻(xiàn)中，此理論都是在應(yīng)力和強(qiáng)度完全獨(dú)立的情況下導(dǎo)出的，但實(shí)際上并不是所有的零件可靠性問(wèn)題中的應(yīng)力和強(qiáng)度完全獨(dú)立，例如軸系零件設(shè)計(jì)變量的荷載、強(qiáng)度等因素之間存在程度不同的相關(guān)性［11］.同時(shí)，在需要考慮構(gòu)件的自重時(shí)，構(gòu)件的應(yīng)力和強(qiáng)度之間也存在相關(guān)性［12］.喻天翔等［13］通過(guò)非線性變換，建立了僅考慮應(yīng)力、強(qiáng)度兩個(gè)隨機(jī)變量相關(guān)時(shí)的零件單模失效可靠度模型，并探討了相關(guān)系數(shù)對(duì)零件單模可靠度的影響及相對(duì)誤差，但假設(shè)隨機(jī)變量的分布都為正態(tài)分布且只考慮應(yīng)力、強(qiáng)度兩個(gè)變量相關(guān).

引起機(jī)械零件廣義應(yīng)力與強(qiáng)度隨機(jī)性的因素主要有材料、加工、制造、安裝、荷載等，如同種材料性能分布的不均勻、制造精度誤差.正是由于這些參數(shù)的隨機(jī)性才有了可靠度的概念.要想得到這些因素的實(shí)際隨機(jī)性參數(shù)是比較困難的，因此在理論分析中常常假設(shè)這些因素服從常見(jiàn)的分布，如正態(tài)分布、威布爾分布、指數(shù)分布等.現(xiàn)有的大多數(shù)文獻(xiàn)中假設(shè)隨機(jī)參數(shù)服從正態(tài)分布，但很多情況下并非如此.這時(shí)就需要探求隨機(jī)變量因素服從其他分布時(shí)的可靠度計(jì)算公式，探求將非正態(tài)分布轉(zhuǎn)化為正態(tài)分布的方法，利用正態(tài)分布運(yùn)算的成熟的計(jì)算技術(shù)來(lái)求得零件可靠度.

本文針對(duì)引起機(jī)械零件單模失效的隨機(jī)變量為不相關(guān)正態(tài)隨機(jī)變量、相關(guān)正態(tài)隨機(jī)變量、不相關(guān)非正態(tài)隨機(jī)變量、相關(guān)非正態(tài)隨機(jī)變量4種情況，借鑒結(jié)構(gòu)可靠性求解理論，尋求建立機(jī)械零件單模失效可靠度求解模型的統(tǒng)一方法.主要是建立相關(guān)非正態(tài)隨機(jī)變量的可靠度求解理論模型.不相關(guān)正態(tài)隨機(jī)變量的可靠度理論是求解其他3種情況的基礎(chǔ).最后，通過(guò)齒輪傳動(dòng)的實(shí)例說(shuō)明本文所提方法的有效性.

1 零件單模失效可靠度求解統(tǒng)一模型建立

全面考慮引起機(jī)械零件單模失效的各個(gè)因素：隨機(jī)變量是否服從正態(tài)分布，隨機(jī)變量之間是否具有相關(guān)性，隨機(jī)變量之間是否為線性關(guān)系.機(jī)械零件單模失效可靠度求解統(tǒng)一模型框圖如圖1所示.設(shè)零件單模失效的極限狀態(tài)方程為M＝G（X），其中X＝（X1X2…Xn）T為隨機(jī)變量，它們共同影響失效狀態(tài)函數(shù)中的應(yīng)力強(qiáng)度.這些隨機(jī)變量中可能含有非正態(tài)隨機(jī)變量，各個(gè)隨機(jī)變量之間可能存在相關(guān)性.下面將對(duì)統(tǒng)一模型由簡(jiǎn)單到復(fù)雜展開(kāi)說(shuō)明.

圖1 機(jī)械零件單模失效可靠度模型Fig.1 Single failure mode reliability model of the mechanical components

1.1 隨機(jī)變量正態(tài)分布不相關(guān)時(shí)零件單模可靠度求解理論

此為求解零件可靠度最簡(jiǎn)單也是基礎(chǔ)的模型，如圖1中Ⅰ框所示，計(jì)算步驟如下：

步驟1 正態(tài)隨機(jī)變量正則化為標(biāo)準(zhǔn)正態(tài)隨機(jī)變量.

假設(shè)影響極限狀態(tài)方程的隨機(jī)變量為Y＝（Y1Y2…Yn）T，極限狀態(tài)方程為

其中Yi～N（μi，σ2i），各隨機(jī)變量不相關(guān)，通過(guò)式（2）正則化為標(biāo)準(zhǔn)正態(tài)隨機(jī)變量Z＝（Z1Z2…Zn）T，則極限狀態(tài)方程轉(zhuǎn)化為式（3）的形式：

步驟2 零件單模可靠度的求解.

將極限狀態(tài)方程（1）以正則化后的標(biāo)準(zhǔn)正態(tài)隨機(jī)變量表示為式（3），則式（3）分為兩種情況：隨機(jī)變量Zi的線性組合或非線性組合，下面分別表述：

（1）若極限狀態(tài)方程（3）為n維標(biāo)準(zhǔn)正態(tài)隨機(jī)變量Zi的線性組合：

可靠度指數(shù)

可靠度

（2）若極限狀態(tài)方程（3）為非線性組合，則可采用兩種方法求解.

①一 次 二 階 矩（first－order second－moment，F(xiàn)OSM）法［17］.

將式（3）在平均值處一階泰勒展開(kāi)，僅保留一階項(xiàng)：

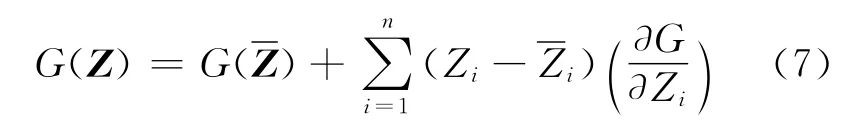
則

零件單模可靠度可由式（5）、（6）求得.

②改進(jìn)的一次二階矩（advanced first－order second－moment，AFOSM）法［18］.

通過(guò)求解式（9）得到可靠度指數(shù)β，代入式（6）求得可靠度.對(duì)于式（9）的求解可以采用Lagrange乘子迭代法導(dǎo)出的公式進(jìn)行迭代計(jì)算，將在2.1中詳細(xì)介紹.

1.2 隨機(jī)變量正態(tài)分布相關(guān)時(shí)零件單模可靠度求解理論

假設(shè)影響極限狀態(tài)方程的隨機(jī)變量為X＊＝（X＊1X＊2…X＊n）T，極限狀態(tài)方程為

步驟1 正態(tài)隨機(jī)變量正則化為標(biāo)準(zhǔn)正態(tài)隨機(jī)變量.

按照式（2）、（3）的形式將相關(guān)的非標(biāo)準(zhǔn)正態(tài)隨機(jī)變量X＊＝（X＊1X＊2…X＊n）T正則化為相關(guān)的標(biāo)準(zhǔn)正態(tài)隨機(jī)變量Y＊＝（Y＊1Y＊2…Y＊n）T，然后根據(jù)下述步驟2、步驟3進(jìn)行零件單模可靠度的求解.

步驟2 相關(guān)的標(biāo)準(zhǔn)正態(tài)隨機(jī)變量轉(zhuǎn)化為不相關(guān)的正態(tài)隨機(jī)變量.

將相關(guān)的標(biāo)準(zhǔn)正態(tài)隨機(jī)變量Y＊＝（Y＊1Y＊2…Y＊n）T線性變換為不相關(guān)的正態(tài)隨機(jī)變量Y＝（Y1Y2…Yn）T，Yi～N（μi，σi2）.

變換過(guò)程如下：

設(shè)隨機(jī)變量Y＊＝（Y＊1Y＊2…Y＊n）T的協(xié)方差矩陣為

由線性代數(shù)理論可知，矩陣CY＊ 可通過(guò)式（12）線性變換成對(duì)角矩陣：

其中A是一個(gè)正交矩陣，它的列向量等于矩陣CY＊ 的特征向量，對(duì)角矩陣CY由式（13）計(jì)算：

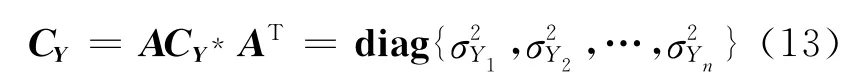
對(duì)角矩陣CY的對(duì)角元素σ2Yi等于矩陣CY＊ 的第i個(gè)特征值.由式（12）可得互不相關(guān)的正態(tài)隨機(jī)變量Y＝（Y1Y2…Yn）T.

步驟3 變量正態(tài)分布相關(guān)時(shí)零件單模可靠度求解.

經(jīng)過(guò)步驟1、步驟2所述方法變換后，可靠度的求解轉(zhuǎn)化為1.1中討論的問(wèn)題，按照1.1中提供的方法就可以得到考慮隨機(jī)變量正態(tài)分布且相關(guān)時(shí)的零件單模失效下的可靠度.

1.3 含有非正態(tài)隨機(jī)變量且相關(guān)時(shí)零件單模可靠度求解理論

研究發(fā)現(xiàn)，自然界中大多數(shù)的物理量在經(jīng)過(guò)無(wú)數(shù)次的統(tǒng)計(jì)分析后都近似服從正態(tài)分布，因此有關(guān)正態(tài)分布函數(shù)的性質(zhì)、特征、數(shù)字特征等研究也最多，發(fā)展了許多可用的結(jié)論及大量的可供參考查閱的數(shù)據(jù).基于此現(xiàn)行對(duì)于由高維極限狀態(tài)函數(shù)表示的可靠度關(guān)系式的求解都是以各隨機(jī)變量服從正態(tài)分布為前提下得出的.然而面對(duì)多維極限狀態(tài)函數(shù)中含有非正態(tài)隨機(jī)變量的情形，只有將非正態(tài)隨機(jī)變量轉(zhuǎn)化為正態(tài)隨機(jī)變量，才能利用現(xiàn)有成熟的、計(jì)算精度高的可靠度理論進(jìn)行機(jī)械零件可靠度的求解，本節(jié)將對(duì)隨機(jī)變量中含有非正態(tài)隨機(jī)變量的情形進(jìn)行研究.

假設(shè)機(jī)械零件單模失效的極限狀態(tài)方程為

其中X＝（X1X2…Xn）T，為影響應(yīng)力、強(qiáng)度分布的隨機(jī)變量，X中含有非正態(tài)隨機(jī)變量且各隨機(jī)變量之間具有相關(guān)性.此種情況下機(jī)械零件單模失效可靠度求解步驟如下：

步驟1 將X中的非正態(tài)隨機(jī)變量轉(zhuǎn)化為正態(tài)隨機(jī)變量.

（1）Rosenblatt變換（Rosenblatt transformation，RT）［14］

Rosenblatt證明：任意非正態(tài)隨機(jī)變量X，理論上都可以通過(guò)Rosenblatt變換轉(zhuǎn)化為線性無(wú)關(guān)的標(biāo)準(zhǔn)正態(tài)隨機(jī)變量Z.但這種變換具有局限性，需要知道n維隨機(jī)變量X的聯(lián)合累積分布函數(shù)，具體變換形式如下：

設(shè)n維隨機(jī)變量X的聯(lián)合累積分布函數(shù)為FX（X），則n維標(biāo)準(zhǔn)正態(tài)線性無(wú)關(guān)隨機(jī)變量Z可以通過(guò)式（15）得到：

按順序反求式（15）中的方程，可以得到n維標(biāo)準(zhǔn)正態(tài)線性無(wú)關(guān)隨機(jī)變量Z：

式（16）中的條件概率密度函數(shù)通過(guò)聯(lián)合概率密度函數(shù)按式（17）、（18）求得：

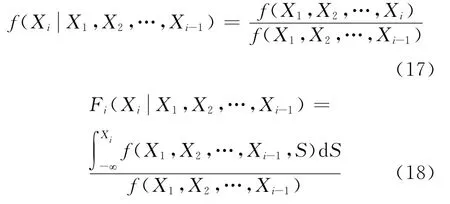
同理可通過(guò)逆變換按順序反求式（16）得到X＝（X1X2…Xn）T.由式（16）變換求得不相關(guān)標(biāo)準(zhǔn)正態(tài)隨機(jī)變量Z＝（Z1Z2…Zn）T.

（2）R－F變換［15］

設(shè)Xi為臨界破壞面上的特定點(diǎn)，通過(guò)令原始分布FXi（Xi）和當(dāng)量正態(tài)分布在特定點(diǎn)Xi處具有相等的概率密度函數(shù)和累積分布函數(shù)，則可求得當(dāng)量正態(tài)分布的均值和標(biāo)準(zhǔn)差

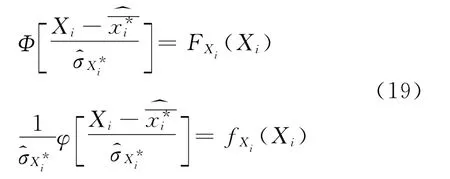
由式（19）得

變換得到正態(tài)隨機(jī)變量X＊＝ （X＊1X＊2…X＊n）T.

步驟2 含有非正態(tài)隨機(jī)變量且相關(guān)時(shí)零件單模可靠度求解.

利用Rosenblatt變換方法進(jìn)行非正態(tài)隨機(jī)變量的正態(tài)化時(shí)，必須利用隨機(jī)變量的聯(lián)合概率密度函數(shù)，這一點(diǎn)在實(shí)際中較難實(shí)現(xiàn)；但經(jīng)過(guò)此種變換后，含有非正態(tài)隨機(jī)變量且相關(guān)的隨機(jī)變量經(jīng)轉(zhuǎn)換后直接轉(zhuǎn)化為不相關(guān)的標(biāo)準(zhǔn)正態(tài)隨機(jī)變量，此時(shí)利用1.1中所述的方法就可以快速地求出其可靠度.

R－F變換方法簡(jiǎn)單，較容易在計(jì)算機(jī)上實(shí)現(xiàn)，并不需要聯(lián)合概率密度函數(shù).將非正態(tài)隨機(jī)變量正則化為標(biāo)準(zhǔn)正態(tài)隨機(jī)變量Y＊＝ （Y＊1Y＊2…Y＊n）T；然后按照1.2中所述方法將相關(guān)正則化正態(tài)隨機(jī)變量Y＊＝ （Y＊1Y＊2…Y＊n）T線性變換為不相關(guān)正態(tài)隨機(jī)變量Y＝ （Y1Y2…Yn）T；最后按照1.1中所述方法求解得到考慮隨機(jī)變量為非正態(tài)分布且相關(guān)時(shí)機(jī)械零件單模可靠度值.

2 機(jī)械零件單模失效可靠度求解算法

本章將根據(jù)第1章介紹的機(jī)械零件單模失效可靠度求解統(tǒng)一模型理論探討可靠度求解的計(jì)算機(jī)實(shí)現(xiàn)算法，機(jī)械零件單模極限狀態(tài)方程為式（14）描述的n維方程，含有非正態(tài)隨機(jī)變量，且各隨機(jī)變量之間存在相關(guān)性.算法中非正態(tài)隨機(jī)變量利用R－F變換方法正則化為正態(tài)隨機(jī)變量；可靠度指數(shù)β的求解采用H－L 方法，利用Lagrange乘子迭代法導(dǎo)出的公式進(jìn)行迭代計(jì)算.

2.1 Lagrange乘子迭代法推導(dǎo)

Lagrange乘子迭代法詳細(xì)敘述如下：

設(shè)

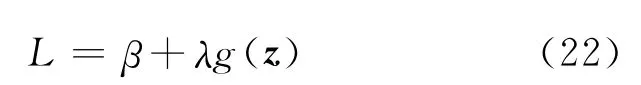
求L的極小值得

令

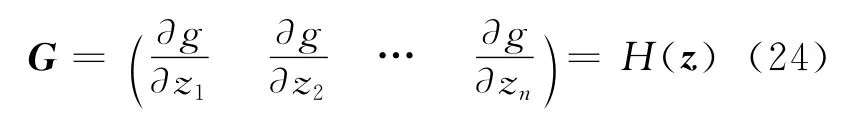
則式（23）可表示為

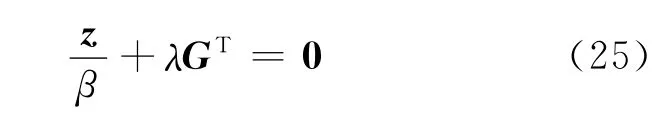
因此

所以

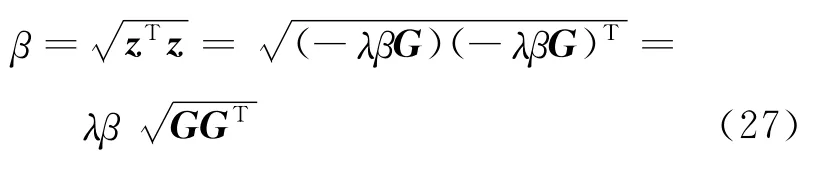
則

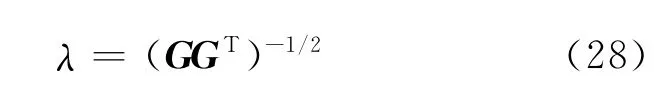
將式（28）代入式（26）得

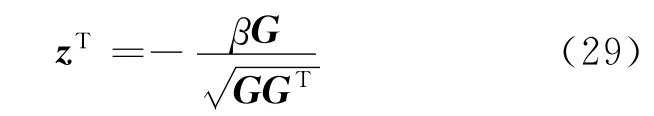
將式（29）代入式（21）得

采用數(shù)值方法可以計(jì)算出

則式（24）、（29）、（30）即可組成Lagrange乘子迭代法計(jì)算的迭代公式.

2.2 機(jī)械零件單模可靠度求解算法

假設(shè)影響零件單模可靠度的非正態(tài)隨機(jī)變量為X＝（X1X2…Xn）T，由以上敘述得到可靠度求解算法的完整步驟如下：

步驟1 設(shè)置初始點(diǎn)x＝（x1x2…xn）T.

步驟2 在設(shè)計(jì)點(diǎn)x＝（x1x2…xn）T處利用式（19）、（20）進(jìn)行R－F 變換，得到，將非正態(tài)隨機(jī)變量在xi處轉(zhuǎn)換為正態(tài)隨機(jī)變量x＊i.

步驟4 對(duì)相關(guān)的標(biāo)準(zhǔn)正態(tài)隨機(jī)變量y＊＝（y＊1y＊2…y＊n）T按照式（11）～（13）線性變換為互不相關(guān)的正態(tài)隨機(jī)變量y＝ （y1y2…yn）T.

步驟5 將y＝（y1y2…yn）T由式（2）正則化為互不相關(guān)的標(biāo)準(zhǔn)正態(tài)隨機(jī)變量z＝（z1z2…zn）T，形成臨界破壞面g（z）＝0.

步驟6 在z處計(jì)算

步驟7 將zT＝βηα代入g（z）＝0并解得β＝β＋min.

步驟8 采用步驟7計(jì)算得到的β重新計(jì)算zT＝βηα.

重復(fù)步驟6～8直到計(jì)算結(jié)果收斂（以z穩(wěn)定作為收斂指標(biāo)）.

步驟12 由式（5）求得可靠度指數(shù)，式（6）求得機(jī)械零件單模失效可靠度.

3 算 例

本文以某1.6 MW 風(fēng)力發(fā)電機(jī)平行級(jí)直齒圓柱齒輪傳動(dòng)為研究對(duì)象，通過(guò)對(duì)風(fēng)機(jī)齒輪箱傳動(dòng)系統(tǒng)受力分析得到直齒圓柱齒輪傳動(dòng)各項(xiàng)參數(shù)：齒輪材料及熱處理為17CrNiMo6低碳合金鋼、滲碳淬火，小齒輪轉(zhuǎn)矩T1＝2.542 8×107N·mm，小齒輪轉(zhuǎn)速n1＝1 600r／min，齒數(shù)Z1＝19，Z2＝94，齒輪模數(shù)m＝12mm，齒寬系數(shù)φd＝0.4，重合度εa＝1.36，齒輪精度7 級(jí)，表面粗糙度Ra＝3.2，使用壽命為20a，高速、輕微振動(dòng).本文僅針對(duì)齒輪傳動(dòng)的齒面接觸疲勞可靠性進(jìn)行分析.

按國(guó)家標(biāo)準(zhǔn)規(guī)定的方法計(jì)算或查線圖得到與齒面接觸疲勞可靠性相關(guān)各參量的均值［19］和文獻(xiàn)［20］中給出的方法估算原則得到各參量的均值和標(biāo)準(zhǔn)差如下：Ft＝（81 785.964 9，4 089.298 2）N，d1＝（228，1.14）mm，b＝（91.2，0.456）mm，KV＝（1.323，0.145 5），KHβ＝（1.348 4，0.044 5），KHα＝（1.225 4，0.040 4），ZV＝（0.949 2，0.031 3），KA＝（1.5，0.049 5），σHlim＝（1 450，174）MPa，ZN＝（1，0.033），ZL＝（1，0.033），ZR＝（2.783 6，0.091 9），ZW＝（1，0.005），ZX＝（0.958，0.004 8），ZH＝（2.494 6，0.012 473），ZE＝（189.8，0.949）定義極限狀態(tài)方程為

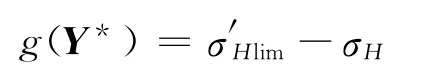
以上各參數(shù)的含義及應(yīng)力σH、強(qiáng)度σ′Hlim的計(jì)算式參考國(guó)家標(biāo)準(zhǔn)GB 3480—1997.下面分3 種情況對(duì)該齒輪傳動(dòng)的可靠度進(jìn)行求解.

（1）假設(shè)各隨機(jī)變量均服從正態(tài)分布，其均值和方差如前所述，各隨機(jī)變量之間相互獨(dú)立，此種情況下根據(jù)文獻(xiàn)［21］提供的方法計(jì)算得到可靠度指標(biāo)β＝1.374 112，R＝0.915 330 5.

（2）假設(shè)各隨機(jī)變量均服從正態(tài)分布，相關(guān)隨機(jī)變量之間的相關(guān)性以齒面接觸疲勞應(yīng)力－強(qiáng)度干涉理論中應(yīng)力σH與強(qiáng)度σ′Hlim之間的相關(guān)性代替，相關(guān)系數(shù)為ρ.由文獻(xiàn)［21］方法得到該齒輪傳動(dòng)的齒面接觸疲勞應(yīng)力S為σH～N（2 887.905 4，205.214 62），齒面接觸疲勞強(qiáng)度δ為σ′Hlim～N（3 670.270 5，531.088 12），則得到可靠度指標(biāo)

當(dāng)相關(guān)系數(shù)ρ在區(qū)間［－1，1］內(nèi)變化，得到可靠度指數(shù)β、可靠度R隨ρ變化曲線如圖2所示.

圖2 ρ－β、ρ－R 曲線Fig.2 ρ－β，ρ－Rcurves

由圖2可知，在相關(guān)系數(shù)ρ從－1 增大到1（即應(yīng)力、強(qiáng)度相互獨(dú)立到應(yīng)力、強(qiáng)度完全相關(guān)）時(shí)，可靠度指數(shù)β從1.063 1增大到2.400 8，相應(yīng)的可靠度R從0.856 010增大到0.991 802，可靠度R的相對(duì)變化率為15.86%，變化較大.此時(shí)若忽略應(yīng)力、強(qiáng)度之間的相關(guān)性將會(huì)產(chǎn)生兩種結(jié)果：若實(shí)際為正相關(guān)，此時(shí)利用獨(dú)立假設(shè)理論就會(huì)低估系統(tǒng)本身可靠性，通過(guò)改變?cè)O(shè)計(jì)來(lái)提高其可靠度時(shí)設(shè)計(jì)成本增高，造成不必要的浪費(fèi)；若實(shí)際為負(fù)相關(guān)，則高估了系統(tǒng)的可靠性，按照此可靠性設(shè)計(jì)的產(chǎn)品，因過(guò)早的失效破壞而達(dá)不到設(shè)計(jì)要求.

以簡(jiǎn)單的應(yīng)力、強(qiáng)度雙變量相關(guān)的模型為基礎(chǔ)，分析相關(guān)系數(shù)對(duì)不同零件單模可靠度的影響.以應(yīng)力、強(qiáng)度相互獨(dú)立時(shí)可靠度為基準(zhǔn)，求解可靠度隨相關(guān)系數(shù)在［0，1］內(nèi)的變化曲線，通過(guò)對(duì)多種具有不同基準(zhǔn)可靠度的機(jī)械零件ρ－R曲線分析知，基準(zhǔn)可靠度越小，考慮與不考慮相關(guān)系數(shù)時(shí)的可靠度差別越大.因此可以得出結(jié)論，當(dāng)在假設(shè)變量相互獨(dú)立情況下求得的可靠度較大時(shí)（如0.999），變量之間的相關(guān)性可以忽略，以它們相互獨(dú)立求得可靠度，這樣不僅簡(jiǎn)化了計(jì)算，還不會(huì)影響機(jī)械零件可靠性?xún)?yōu)化設(shè)計(jì)的精度.

（3）假設(shè)各隨機(jī)變量服從正態(tài)分布，通過(guò)分析國(guó)家標(biāo)準(zhǔn)GB 3480—1997 中各隨機(jī)參數(shù)的計(jì)算知某些隨機(jī)變量之間具有相關(guān)性：Ft、KV、KHα、KHβ、ZV、b與d1具有相關(guān)性；KHβ與b具有相關(guān)性.

定義可靠度極限狀態(tài)方程中各隨機(jī)變量為

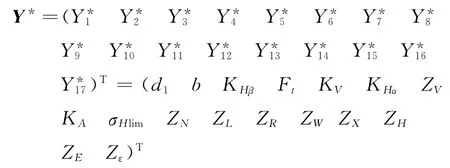
根據(jù)各隨機(jī)變量計(jì)算式設(shè)定相關(guān)隨機(jī)變量相關(guān)系數(shù)為

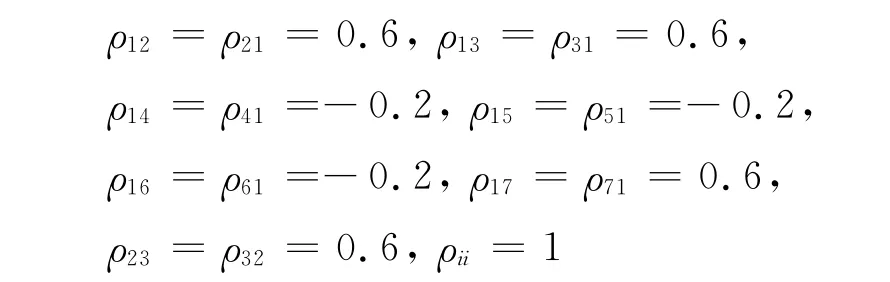
假設(shè)相關(guān)隨機(jī)變量線性變換為非相關(guān)變量后的隨機(jī)變量為z＝（z1z2…zn）T，利用本文介紹的求解算法求解此種情況下的可靠度，設(shè)初始值為z＝（1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1）T，以前后兩次迭代z向量之間的距離作為收斂判據(jù)：經(jīng)過(guò)3次迭代后可靠度指數(shù)β穩(wěn)定在4.216 7，并且經(jīng)過(guò)6次迭代后距離L達(dá)到7.637 1×10－5.所以求得的可靠度為R＝Φ（4.216 7）＝0.999 987 6.

（4）假設(shè)隨機(jī)變量Ft、KV、KHα、KHβ、ZV、b、d1服從對(duì)數(shù)正態(tài)分布，7個(gè)變量間的相關(guān)性情況與（3）中所述相同；其他隨機(jī)變量服從正態(tài)分布；所有隨機(jī)變量的均值和標(biāo)準(zhǔn)差同上.利用本文介紹的求解算法，求解此種情況下的可靠度.外層經(jīng)5次循環(huán)，內(nèi)層循環(huán)分別為63、65、67、68、69次時(shí)，可靠度指數(shù)β穩(wěn)定在4.202 1，此時(shí)精度為1×10－6.所以求得的可靠度為R＝Φ（4.202 1）＝0.999 987 2.

由以上討論可知，本文介紹的變量相關(guān)的機(jī)械零件單模可靠度求解算法是可行的，且具有較高的收斂速度，對(duì)于復(fù)雜的變量相關(guān)的可靠度的求解具有重要的應(yīng)用價(jià)值.另外，從考慮各個(gè)變量之間的相關(guān)性與將只考慮廣義應(yīng)力、強(qiáng)度之間單相關(guān)性求得的可靠度可以看出，差別很大，因此在求解變量相關(guān)可靠度時(shí)，為使求得的可靠度比較精確，應(yīng)盡量將各個(gè)相關(guān)變量的相關(guān)性做單獨(dú)處理，不要將其等效為應(yīng)力、強(qiáng)度之間的相關(guān)性.

4 結(jié) 論

（1）本文以系統(tǒng)中機(jī)械零件的單模失效為研究對(duì)象，通過(guò)探討影響單模失效極限狀態(tài)方程的隨機(jī)變量的不同特征：是否含有非正態(tài)隨機(jī)變量、隨機(jī)變量間是否相關(guān)，建立了考慮含有非正態(tài)隨機(jī)變量和隨機(jī)變量具有相關(guān)性時(shí)的機(jī)械零件單模失效下可靠度求解的統(tǒng)一模型，并對(duì)統(tǒng)一模型求解的理論進(jìn)行了詳細(xì)的論述.

（2）基于所建立的機(jī)械零件單模失效下的可靠度求解統(tǒng)一模型，提出了高效的計(jì)算機(jī)求解算法.

（3）通過(guò)算例說(shuō)明了隨機(jī)變量之間的相關(guān)性對(duì)零件單模失效可靠度的影響，表明在零件單模失效求解中忽略隨機(jī)變量的相關(guān)性將會(huì)帶來(lái)較大的誤差.通過(guò)分析得到，當(dāng)基準(zhǔn)可靠度較大時(shí)（如0.999 9），變量之間的相關(guān)性可以忽略，這樣在不影響優(yōu)化設(shè)計(jì)精度的前提下簡(jiǎn)化了可靠度的計(jì)算.

（4）本文提出的理論為含有非正態(tài)隨機(jī)變量時(shí)零件單模失效下可靠度的求解提供了一個(gè)很好的方法.實(shí)例證明，所提出的計(jì)算機(jī)實(shí)現(xiàn)算法收斂速度快，具有很強(qiáng)的實(shí)用性.

本文所建立的機(jī)械零件單模失效下可靠度求解模型可應(yīng)用于機(jī)械零件任意一種失效模式下的可靠度求解，如熱疲勞、磨損、溫度失效等，這對(duì)機(jī)械零件考慮多模失效下可靠度理論的發(fā)展也具有指導(dǎo)作用.

［1］ Cornell C A.Bounds on the reliability of structural systems［J］.Journal of Structural Division，1967，93（1）：171－200.

［2］ Ditlevsen O.Narrow reliability bounds for structural systems ［J］.Journal of Structural Mechanics，1979，7（4）：453－472.

［3］ FENG Yuan－sheng.A method for computing structural system reliability with high accuracy［J］.Computers ＆Structures，1989，33（1）：1－5.

［4］ 董 聰.現(xiàn)代結(jié)構(gòu)系統(tǒng)可靠性理論［D］.西安：西北工業(yè)大學(xué)，1993.DONG Cong.The reliability theory of modern structural system ［D］.Xi′an：Northwestern Polytechnical University，1993.（in Chinese）

［5］ 孫玉秋，張祖明.機(jī)械系統(tǒng)可靠度計(jì)算方法——階段連續(xù)界限理論［J］.機(jī)械設(shè)計(jì)與制造，2001（2）：3－5.SUN Yu－qiu，ZHANG Zu－ming.Reliability calculation method of the mechanical system—phases sequence bounds theory ［J］.Machinery Design ＆ Manufacture，2001（2）：3－5.（in Chinese）

［6］ 喻天翔，孫玉秋，張祖明.多模式失效的機(jī)械零件可靠度計(jì)算新理論［J］.機(jī)械工程學(xué)報(bào)，2003，39（3）：134－138.YU Tian－xiang，SUN Yu－qiu，ZHANG Zu－ming.Reliability computing new theory of mechanical elements with multi failure mode ［J］.Chinese Journal of Mechanical Engineering，2003，39（3）：134－138.（in Chinese）

［7］ 王 正，謝里陽(yáng)，李 兵.多種失效模式下的機(jī)械零件動(dòng)態(tài)可靠性模型［J］.中國(guó)機(jī)械工程，2007，18（18）：2143－2146.WANG Zheng，XIE Li－yang，LI Bing.Timedependent reliability model of component with multiple failure modes ［J］.China Mechanical Engineering，2007，18 （18）：2143－2146.（in Chinese）

［8］ 王 正，謝里陽(yáng)，李 兵.考慮載荷作用次數(shù)的失效相關(guān)系統(tǒng)可靠性模型［J］.東北大學(xué)學(xué)報(bào)：自然科學(xué)版，2007，28（5）：704－707.WANG Zheng，XIE Li－yang，LI Bing.Reliability model of failure－dependent system with frequency of loading taken into account ［J］.Journal of Northeastern University：Natural Science，2007，28（5）：704－707.（in Chinese）

［9］ Neves R A，Mohamed－Chateauneuf A，Venturini W S.Component and system reliability analysis of nonlinear reinforced concrete grids with multiple failure modes［J］.Structural Safety，2008，30（3）：183－199.

［10］ 閆 明，張義民，李 鶴，等.機(jī)械零件相關(guān)失效可靠度計(jì)算的二重積分模型［J］.東北大學(xué)學(xué)報(bào)：自然科學(xué)版，2011，32（10）：1460－1463.YAN Ming，ZHANG Yi－min，LI He，etal.Double integration model for reliability computation of mechanical components at dependent failure modes［J］.Journal of Northeastern University：Natural Science，2011，32（10）：1460－1463.（in Chinese）

［11］ 吳 波.軸的多失效模型與可靠性研究［J］.機(jī)械設(shè)計(jì)，1998，15（6）：47－48，57.WU Bo.Study on the multi－failure mode model and reliability of the shaft ［J］.Journal of Machine Design，1998，15（6）：47－48，57.（in Chinese）

［12］ 何水清，王 善.結(jié)構(gòu)可靠性分析與設(shè)計(jì)［M］.北京：國(guó)防工業(yè)出版社，1993.HE Shui－qing，WANG Shan.Structure Reliability Analysis and Design［M］.Beijing：National Defense Industry Press，1993.（in Chinese）

［13］ 喻天翔，成剛虎，張選生，等.考慮變量相關(guān)的機(jī)械零件可靠度計(jì)算［J］.西安理工大學(xué)學(xué)報(bào)，2003，19（1）：73－75.YU Tian－xiang，CHENG Gang－h(huán)u，ZHANG Xuansheng，etal.Reliability computation of mechanical parts in considering variable correlations ［J］.Journal of Xi′an University of Technology，2003，19（1）：73－75.（in Chinese）

［14］ Rosenblatt M.Remarks on a multivariate transformation ［J］.Annals of Mathematical Statistics，1952，23（3）：470－472.

［15］ Rackwitz R，F(xiàn)iessler B.Structural reliability under combined random load sequences ［J］.Computers and Structures，1978，9（5）：489－494.

［16］ Cramér H.Mathematical Methods of Statictics［M］.New Jersey：Princeton University Press，1999.

［17］ Cornell C A.Structural safety specifications based on second－moment reliability analysis［J］.IABSE Reports of the Working Commissions，1969，4：235－245.

［18］ Hasofer A M，Lind N C.Exact and invariant second－moment code format ［J］.Journal of Engineering Mechanical Division，ASCE，1974，100（EM1）：111－121.

［19］ 《現(xiàn)代機(jī)械傳動(dòng)手冊(cè)》編輯委員會(huì).現(xiàn)代機(jī)械傳動(dòng)手冊(cè)［M］.2版.北京：機(jī)械工業(yè)出版社，2002.Editing Committee of Modern Handbook of Mechanical Transmission.Modern Handbook of Mechanical Transmission ［M］.2nd ed.Beijing：China Machine Press，2002.（in Chinese）

［20］ 張義民.汽車(chē)零部件可靠性設(shè)計(jì)［M］.北京：北京理工大學(xué)出版社，2000.ZHANG Yi－min.Reliability Design of the Auto Components ［M］.Beijing：Beijing Institute of Technology Press，2000.（in Chinese）

［21］ 芮延年，傅戈雁.現(xiàn)代可靠性設(shè)計(jì)［M］.北京：國(guó)防工業(yè)出版社，2007.RUI Yan－nian，F(xiàn)U Ge－yan.Modern Reliability Design ［M］.Beijing：National Defense Industry Press，2007.（in Chinese）