濱海斜坡復式護岸斷面波浪爬坡試驗研究

常 江，柳淑學＊，李金宣，代英男

（1.大連理工大學 海岸和近海工程國家重點實驗室，遼寧 大連 116024；2.中交第一航務工程勘察設計院有限公司，天津 300222）

0 引 言

護岸是保護海岸、河岸和湖岸使其免受水浪的沖擊、侵蝕而構筑的水邊設施［1］.現代護岸設計的內容要廣泛得多，更強調景觀性、親水性和生態性.護岸與濱水的親水設施一道成為內容涉及水利、土木工程、園林景觀和藝術的綜合性的水邊環境設計［2］.護岸的形式多種多樣，采用斜坡式結構是與較差地基和較淺水深等自然條件相適應的一種經濟結構形式.復式斷面護岸是常采用的一種斜坡式護岸結構，其前坡供游人進行親水活動，后坡提供休閑娛樂的場所.從環境與景觀的角度上看，在滿足抵御波浪沖擊、保障護岸安全的前提下，應盡量將護岸實體壓低［3］.

當波浪相對較大時，波浪會沿著護岸斜坡上爬，在坡頂形成爬坡流.波浪爬高是濱海海堤堤頂高程確定的最重要因素［4］，同樣也是堤式護岸堤頂高程確定的關鍵所在.此外，景觀性護岸頂常有與休閑相關的建筑和設施，堤頂爬坡流的厚度往往是這些休閑設施設計的依據之一.波浪爬高的影響因素主要有波浪特性、斜坡坡度、斜坡護面結構形式和斜坡滲透等多種.目前，針對斜坡斷面的波浪爬高，國內外許多學者進行了大量的研究，提出了多種經驗計算方法.其中應用最廣的有我國堤防設計規范中的方法［5］和歐美廣泛應用的van der Meer法［6－8］.這些方法主要針對海堤前斜坡，且復式斷面的前坡和后坡坡度相對較大，普遍大于1∶5，計算的結果為累計率為X%的爬高.而對于濱海護岸，堤頂后方一般為人活動區域，坡度較緩，大多取為3%左右，波浪爬坡流能夠爬到的最大高度或者最大距離對于護岸的設計具有重要的影響.此外，最大爬坡高度和爬坡流厚度與護岸前沿處的越浪量具有直接關系，可以用護岸前沿的越浪量大小來反映.

針對目前工程設計需要，本文基于物理模型試驗，研究不同堤頂高程在不同波浪要素作用下波浪沿濱海護岸斷面爬坡范圍和爬坡流不同位置處的厚度，探討最大爬坡距離和爬坡流厚度的影響因素和其影響規律，建立爬坡距離和爬坡流厚度與護岸前沿越浪量的關系，在此基礎上參考相關研究成果討論比尺效應對試驗結果的影響，以期為工程實際設計和相應數值計算模型的驗證提供參考.

1 試驗概述

越浪量的大小直接決定了濱海護岸頂岸邊波浪的爬坡距離和大小，而護岸越浪量的研究相對比較成熟，因此本研究旨在建立波浪在濱海護岸頂岸邊的爬坡距離和爬坡流厚度與護岸前沿越浪量的關系.試驗針對光面斜坡護岸，在大連理工大學海岸和近海工程國家重點實驗室的海洋環境水槽中進行，水槽長50m，寬3m，高1m，可同時產生波浪和水流.水槽的工作段在縱向分割成0.8 m 和2.2 m 兩個部分，試驗段設在0.8 m 寬 部分.水槽一端裝有由微機控制的液壓伺服造波機，由計算機自動控制產生所要求模擬的波浪.該造波系統可根據需要產生規則波和不同譜型的不規則波.水槽末端設有消浪斜坡和消波裝置.試驗水槽布置示意圖如圖1所示.

測量波浪爬坡高度和爬坡流厚度的試驗布置如圖2所示，堤前水深為0.4m，護岸坡度為1∶2，景觀護岸工程護岸頂岸邊區域考慮排水因素一般設有一定的坡度，但是考慮景觀因素，坡度一般較緩，參考相關實際工程應用，本文試驗研究的岸邊坡度選較為常見的3∶100，試驗模型中的堤頂超高Rc從小到大分別取0.06、0.08、0.10 和0.12m.測量水流厚度采用北京水利科學研究院研制的DJ800多點浪高儀采集處理系統，該系統可同步測量多點水面過程并進行數據分析，誤差小于0.15%，波高分辨精度為±1mm.從堤頂開始，沿護岸每隔50cm 在斜坡上設置一個小水坑，里面灌滿與斜坡平齊的水，深度約5cm，在里面設置浪高儀，當有水流流過測量點時，浪高儀上水面高度發生變化.本試驗中一共設置了11個浪高儀，最大測量范圍為距護岸前沿5.0m.

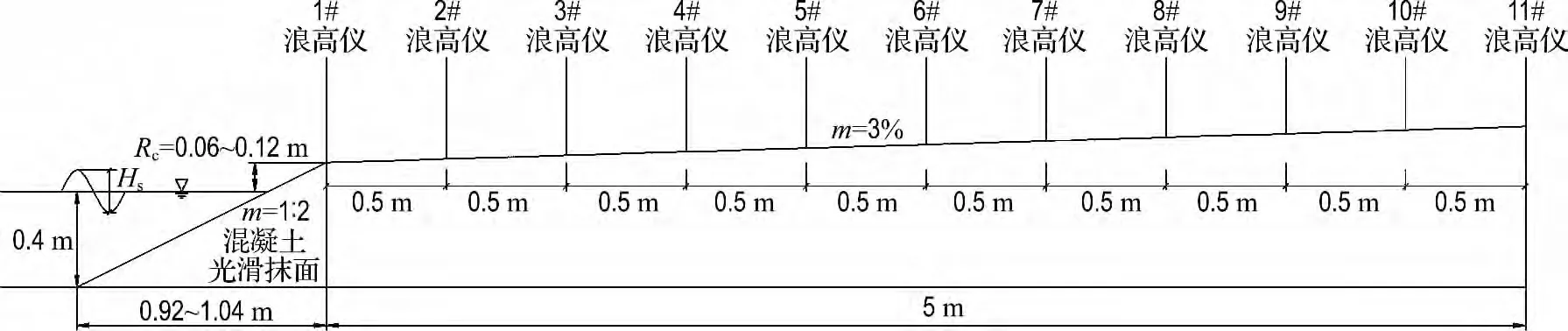
圖2 波浪爬坡試驗布置圖Fig.2 Sketch of the experimental setup for the wave running upon slope revetment

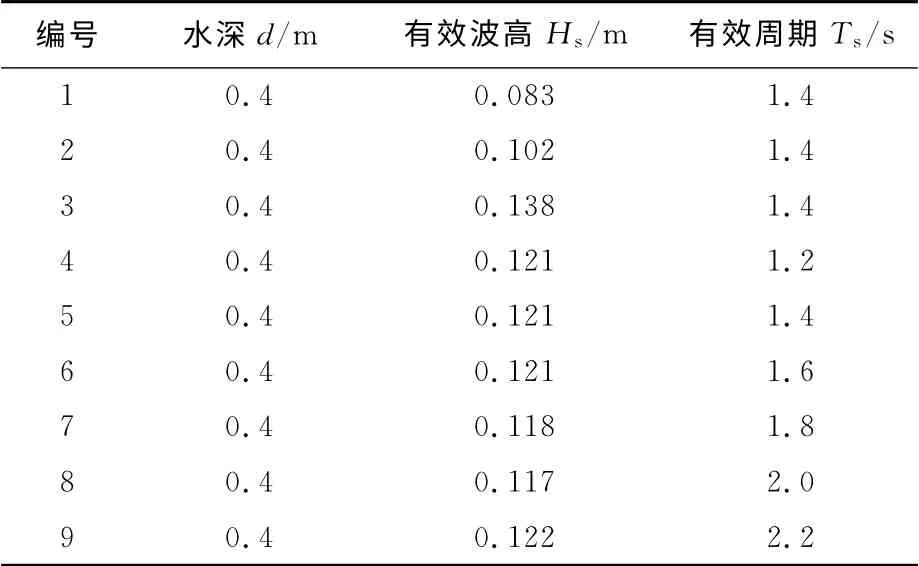
表1 不規則波試驗參數Tab.1 Irregular wave test parameters

試驗采用不規則波，選取在當前水深下較大波高的不同波浪，但未破碎，不規則波波浪要素如表1所示.波浪頻譜采用Goda 改進的JONSWAP譜［9］，時間間隔為0.02s，數據采集長度8 192，周期較長（1.8、2.0 和2.2s）時為16 384，波數為120～180個，每組試驗重復3次.

2 試驗結果分析

2.1 平均越浪量分析

為了研究波浪爬坡高度和爬坡流厚度與護岸前沿平均越浪量的關系，在建立斜坡模型前針對護岸前沿的平均越浪量進行了測量，測試方法和結果可參考代英男等［10］在相關試驗研究中給出的結果.為了驗證試驗所得越浪量結果，將試驗測得量綱一化平均越浪量與《海港水文規范》（JTJ 213—98）、歐洲國家推薦使用的van der Meer（VDM）方法，以及陳國平等給出的方法［11］的計算結果進行比較，結果如圖3所示，圖中給出了量綱一化平均越浪量與相對堤頂超高Rc／Hs的關系.從圖中可以看出，試驗值在規范方法與VDM 方法和陳國平方法之間，略大于規范方法計算結果，變化趨勢與規范方法和陳國平等方法［11］一致.因此可以根據實際需要采用規范方法或陳國平方法［11］來計算護岸前沿的越浪量.

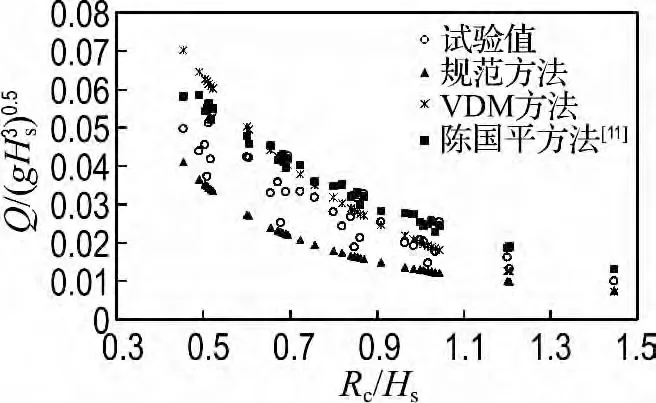
圖3 波浪平均越浪量試驗結果與規范方法、VDM 方法和陳國平方法比較Fig.3 Comparison between experimental results and calculated results by Standard，VDM and Chen Guo－ping methods

2.2 波浪爬坡試驗數據處理

最大爬坡高度是指一組波浪作用下，波浪爬上護岸后能夠爬到的相對護岸前沿的最大高度或者距離，體現了波浪在護岸上的爬坡能力，也反映了斜坡護岸上的最大浸水范圍.為了直觀體現這種爬坡能力，試驗中采用沿護岸能夠爬到的最大距離，用Lmax來表示.在斜坡上目測波浪能夠爬到的最遠位置，測量此位置距斜坡前沿的距離即為波浪沿斜坡的最大爬坡距離.

在不規則波作用下，浪高儀測得的水面高度典型過程線如圖4所示.可以明顯看出，不規則波作用下，爬坡流水面高度也呈現出不規則的變化.如前所述，每個浪高儀放置在斜坡上的小水坑中，里面灌滿與斜坡平齊的水，因此每組試驗中，基準零點為試驗過程中采集到的水面高度最小值，通過計算采集到的水面高度與該基準零點的差得到爬坡流厚度.為了得到穩定的試驗結果，取前1／3個厚度峰值的平均值為研究對象，用hc來表示.此外，在實際工程應用中，最大厚度往往也很重要，所以也研究了每組試驗的最大厚度峰值，用hcmax來表示.為了分析波浪沿護岸最大爬坡距離、爬坡流厚度和各影響因素之間關系，需要將物理量進行量綱一化處理.考慮各物理因素的影響，本文相對最大爬坡距離定義為L＊max＝Lmax／Hs，爬坡流厚度定義為h＊c＝hc／Hs，量綱一化越浪量Q＊＝距護岸前沿相對距離L＊a＝La／Hs，其中La為浪高儀距護岸前沿的距離，Hs為有效波高.

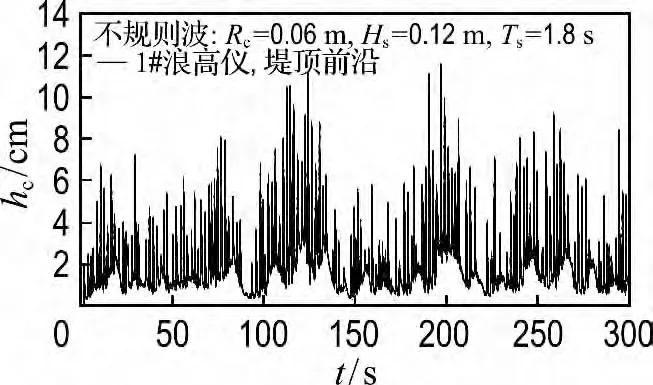
圖4 不規則波作用下護岸上波浪爬坡流的水面過程線Fig.4 The surface course of wave run－up flow on revetment with irregular wave

2.3 最大爬坡距離與護岸前沿平均越浪量關系

圖5給出了試驗所得波浪沿護岸相對最大爬坡距離Lmax／Hs與量綱一化越浪量的關系.從圖中可以看出隨著量綱一化越浪量的增大，相對最大爬坡距離也增大，考慮當越浪量為0時的爬坡距離為0，因此采用冪指數關系擬合后得到的最大爬坡距離Lmax／Hs與量綱一化越浪量的關系為

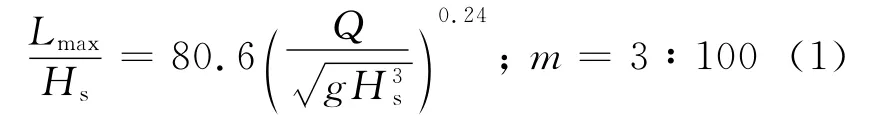
圖6為式（1）的計算結果（Lmax／Hs）c和試驗結果（Lmax／Hs）e的比較，可以看出計算結果和試驗結果符合良好.

2.4 爬坡流厚度與護岸前沿平均越浪量關系

爬坡流厚度取決于護岸前沿平均越浪量和距護岸前沿的距離，因此需要考慮在距護岸前沿相對距離相同的情況下，爬坡流厚度與護岸前沿平均越浪量的關系.圖7給出了不同位置試驗測得的爬坡流厚度與量綱一化越浪量的關系，可以看出，各組次中相對爬坡流厚度隨著平均越浪量的增大而明顯增大.

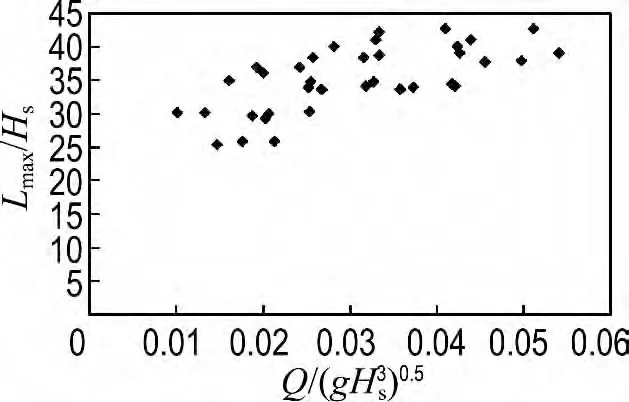
圖5 波浪沿護岸相對最大爬坡距離與護岸前沿量綱一化平均越浪量的關系Fig.5 The relationship between relative maximum wave ascent and the dimensionless average wave overtopping discharge at the front of slope

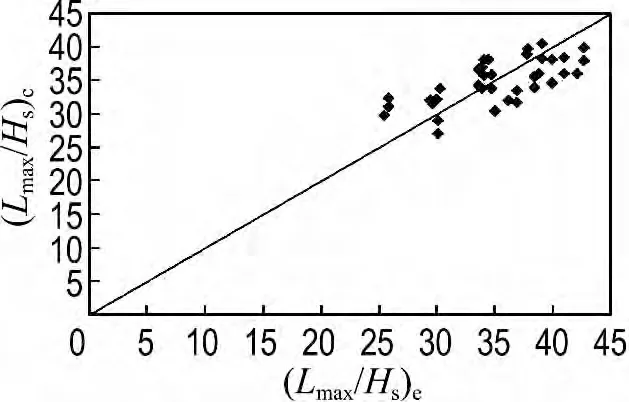
圖6 波浪沿護岸最大爬坡距離試驗值和計算值的比較Fig.6 Comparison between experimental value and calculated value of maximum wave ascent at the front of slope

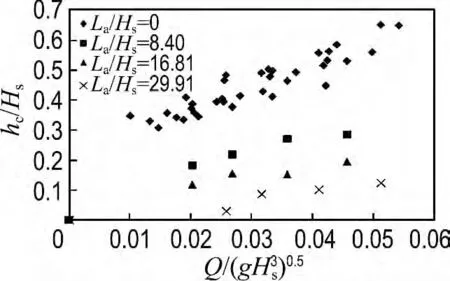
圖7 相對爬坡流厚度與護岸前沿量綱一化平均越浪量的關系Fig.7 The relationship between relative thickness of wave run－up flow and the dimensionless average wave overtopping discharge at the front of slope

2.5 爬坡流厚度與距護岸前沿距離關系

圖8為相同量綱一化越浪量情況下，相對爬坡流厚度hc／Hs與相對距護岸前沿距離La／Hs的關系，可以看出，相對爬坡流厚度隨著相對距護岸前沿距離的增大而明顯減小，并且各試驗結果減小的趨勢大致相同.

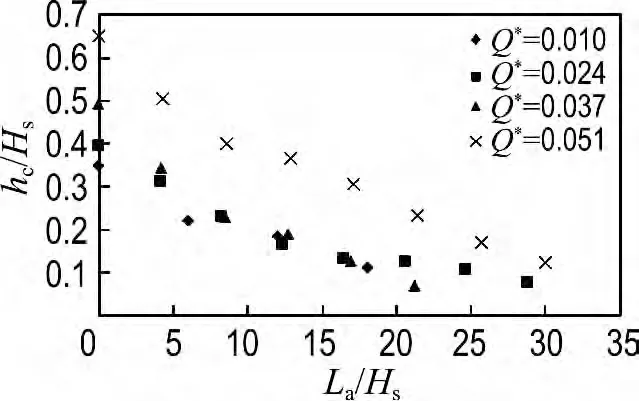
圖8 相對爬坡流厚度與相對距護岸前沿距離的關系Fig.8 The relationship between relative thickness of wave run－up flow and the relative distance from slope front

2.6 爬坡流厚度計算經驗公式

為了得到不同位置處爬坡流厚度計算的經驗公式，首先建立護岸前沿處的爬坡流厚度計算公式，在此基礎上，進一步建立爬坡流厚度沿斜坡衰減系數的公式，因此不同位置處的相對爬坡流厚度可以寫為

式中：hc0／Hs為護岸前沿處的相對爬坡流厚度；Cr為爬坡流厚度沿斜坡的衰減系數，定義為距護岸前沿一定距離處的爬坡流厚度與護岸前沿爬坡流厚度的比，顯而易見，衰減系數Cr受相對距護岸前沿距離La／Hs的影響.

類似于波浪沿斜坡最大爬坡距離的分析，參考圖5，當越浪量為0時，護岸前沿的爬坡流厚度亦為0，可采用冪指數關系來擬合護岸前沿處爬坡流厚度與護岸前沿平均越浪量的關系，得到如下計算公式：

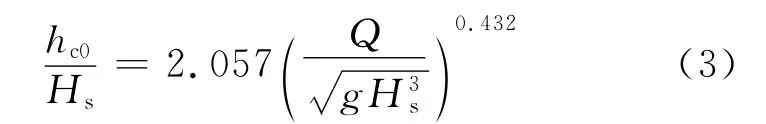
為了得到爬坡流厚度的衰減系數，圖9給出了試驗分析所得Cr隨La／Hs的變化情況.可以看出，隨著La／Hs增大，Cr明顯減小.采用指數關系進行擬合可得到如下關系式：

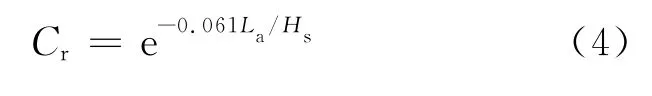
把式（3）和（4）代入式（2），則可以得到波浪沿護岸相對爬坡流厚度hc／Hs與相對距護岸前沿距離La／Hs和護岸前沿量綱一化平均越浪量Q／的關系：

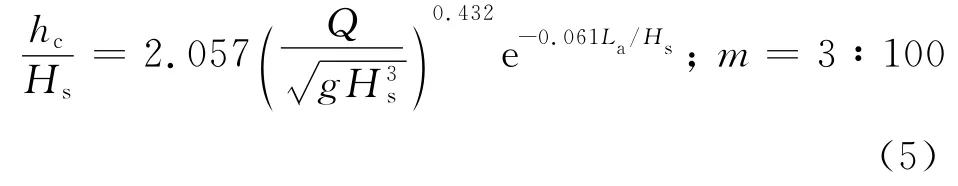
式（5）的計算值和試驗值的比較如圖10 所示，從圖中可以看出，計算值與試驗值符合良好.需要說明的是，式（5）中La／Hs的最大取值為由式（1）計算所得的值.

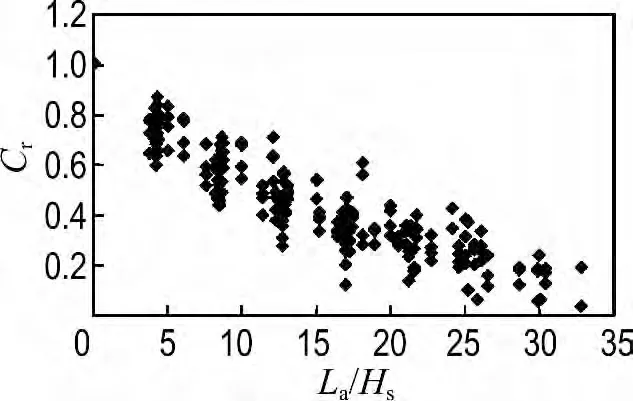
圖9 衰減系數Cr 與相對距護岸前沿距離La／Hs 的關系Fig.9 The reduction degree of flow thickness Cr with the relative distance from slope front La／Hs

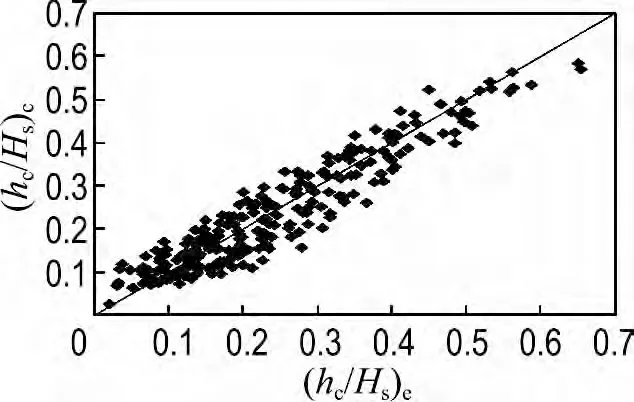
圖10 波浪爬坡流厚度計算值與試驗值的比較Fig.10 The comparison between experimental value and calculated value of thickness of wave run－up flow

2.7 爬坡流最大厚度分析

以上給出的是不規則波作用下爬坡流厚度的有效值（1／3值），為了得到爬坡流的最大值，圖11給出了爬坡流厚度統計的1／3 值（hc）和最大值（hcmax）的關系，可以看出，兩者近似符合線性關系，最大值約為1／3值的1.626倍，即

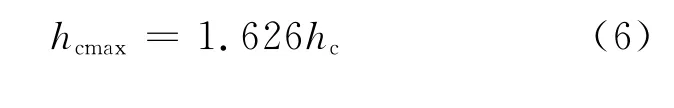
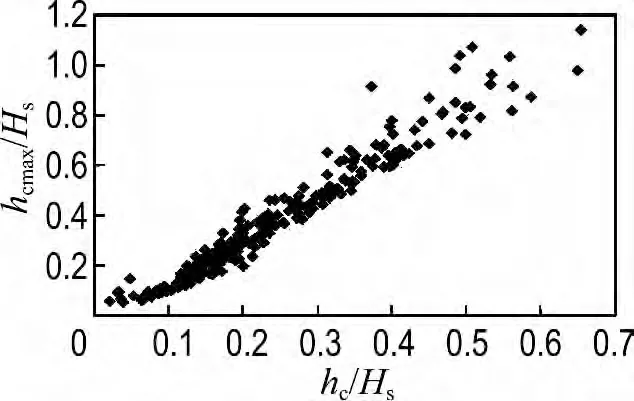
圖11 波浪爬坡流厚度最大值與1／3值的關系Fig.11 The relationship between maximum and 1／3 thickness of wave run－up flow

3 比尺效應的影響分析討論

本文基于模型試驗建立了爬坡流距離和厚度與越浪量之間的關系，由于比尺效應的問題，其對于原型實際工程的適用性需要進一步研究.事實上，由于原型觀測的復雜性，目前相關的研究成果大多是在物理模型試驗研究的基礎上給出的，而試驗的比尺效應對于波浪越浪、爬高、護面塊體穩定等的影響一直是人們關心的問題.

在越浪量研究方面，van der Meer等［12］通過1∶7和1∶35兩個比尺的模型試驗研究，得出兩個比尺下堤前波浪反射情況和越過堤頂波浪個數接近，即越浪量接近，無實質區別.李曉亮［13］在越浪量研究中提到De Rouck等［14］總結的一些海防建筑物原型實測越浪量，將這些結果與一些試驗結果進行對比，認為光滑斜坡堤的比尺效應可以忽略.歐洲《海防建筑物越浪手冊》［15］中也提到，對于光滑斜坡堤，比尺效應調整系數為1.0，即可以不考慮比尺效應的影響.而在波浪爬高方面，歐洲《海防建筑物越浪手冊》［15］中，總結了不同比尺下的波浪在斜坡上的爬高試驗數據，并將其與經驗公式進行對比，認為在不同比尺下波浪爬坡的變化規律相同.楊運澤［16］通過模型試驗研究得出，用小比尺模型試驗，實際爬坡高度會估計得偏小，而Ahrens［17］采用不規則波在光滑斜坡上的爬坡研究中提到Stoa等［18－19］通過比尺為1∶20和1∶40的模型試驗研究，得出爬坡比尺效應調整系數隨結構物坡度的變化.總體來講，在模型比尺1∶20和1∶40條件下，比尺效應的影響取決于結構物的坡度，1∶1.5坡度時最大影響系數為14%，坡度越陡或越緩，比尺效應的影響越小，當坡度小于1∶8時，比尺效應的影響在5%以內.

本文模型試驗的模型設計是在參考相關工程的基礎上進行的，模型試驗的比尺在1∶20～1∶30，因此在應用本文試驗成果時，可以根據實際工程情況，適當考慮比尺效應的影響.

4 結 論

（1）波浪在護岸上后方的最大爬坡距離隨著護岸前沿平均越浪量的增大而增大，并且建立了最大爬坡距離與量綱一化越浪量的關系.

（2）護岸頂爬坡流的厚度與護岸前沿平均越浪量和距護岸前沿距離有關，隨著越浪量的增大，爬坡流厚度增大，隨著距護岸前沿距離的增大，爬坡流厚度減小.

（3）在護岸頂岸邊坡度為3∶100情況下，分別建立了護岸前沿處相對爬坡流厚度與量綱一化平均越浪量的關系以及爬坡流厚度沿斜坡的衰減系數與相對距護岸前沿距離的關系，在此基礎上，建立了爬坡流厚度與護岸前沿平均越浪量和距護岸前沿距離的關系.

（4）分析了在一定越浪量條件下，爬坡流厚度的最大值和1／3 值的關系，總體來講，最大值是1／3值的1.626倍.

（5）基于現有的參考資料和研究成果，分析了比尺效應對于越浪和波浪爬坡等的影響規律，綜合各方面研究成果，對于光滑斜坡，越浪量受比尺效應的影響可以忽略，但比尺效應對于波浪的爬坡具有一定的影響，其影響取決于結構的坡度，坡度在1∶1.5時最大在14%左右，當坡度小于1∶8時，比尺效應的影響在5%以內.

本文參考相應實際工程進行了護岸頂岸邊坡度為3∶100的模型試驗，研究成果可以為相應數值模型提供驗證依據，同時也可以為相關工程設計提供基本的參考.總體來講，在護岸前沿越浪量一定的情況下，坡度越緩，爬坡距離越大，沿程厚度越小.不同坡度堤壩情況下的爬坡流厚度和距離還應進一步研究.

［1］ 河川治理中心.濱水地區親水設施規劃設計［M］.北京：中國建筑工業出版社，2005.Center for River Governance.Water Affinity Facilities Planning and Design of Waterfront［M］.Beijing：China Building Press，2005.

［2］ 張丙印，倪廣恒.城市水環境工程［M］.北京：清華大學出版社，2005.ZHANG Bing－yin，NI Guang－heng.City Water Environment Engineering ［M］.Beijing：Tsinghua University Press，2005.

［3］ 何元瑭，陸明生.新型景觀護岸結構設計［J］.水運工程，2005（4）：39－41.HE Yuan－tang，LU Ming－sheng.A new－type landscape revetment structural design［J］.Port ＆Waterway Engineering，2005 （4）：39－41.（in Chinese）

［4］ 苗 青，江 洧.波浪在海堤上的爬高及消浪措施研究綜述［J］.廣東水利水電，2007（6）：5－7，22.MIAO Qing，JIANG Wei.The review of studies of wave run－up on seawall and wave dissipation measures ［J］.Guangdong Water Resources and Hydropower，2007（6）：5－7，22.（in Chinese）

［5］ 水利部水利水電規劃設計總院.GB 50286—98 堤防工程設計規范 ［S］.北京：中國計劃出版社，1998.China Renewable Energy Engineering Institute.GB 50286－98Code for Design of Levee Project［S］.Beijing：China Planning Press，1998.（in Chinese）

［6］ U.S.Army Corps of Engineers.Coastal Engineering Manual，Engineer Manual 1110－2－1110［M］.Washington D C：U.S.Army Corps of Engineers，2004.

［7］ Krystian W P.Dikes and Revetments Design：Maintenance and Safety Assessment ［M ］.Rotterdam：A.A.Balkema，1998：43－52.

［8］ Krystian W P.Geosynthetics and Geosystems in Hydraulic and Coastal Engineering［M］.Rotterdam：A.A.Balkema，2000：25－26.

［9］ Goda Y.A comparative review on the functional forms of directional wave spectrum ［J］.Coastal Engineering Journal，1999，41（1）：1－20.

［10］ 代英男，柳淑學，常 江，等.斜坡堤越浪流厚度及堤后次生波的試驗研究［J］.水運工程，2011（12）：1－5.DAI Ying－nan，LIU Shu－xue，CHANG Jiang，et al.Experimental research on layer thickness of wave overtopping flow and secondary wave conditions over sloping breakwater ［J］.Port ＆Waterway Engineering，2011（12）：1－5.（in Chinese）

［11］ 陳國平，周益人，嚴士常.不規則波作用下海堤越浪量試驗研究［J］.水運工程，2010（3）：1－6.CHEN Guo－ping，ZHOU Yi－ren，YAN Shi－chang.Test study on wave overtopping under irregular wave action ［J］.Port ＆ Waterway Engineering，2010（3）：1－6.（in Chinese）

［12］ van der Meer J W，Veldman J J.Singular points at berm breakwaters：scale effects，rear，round head and longshore transport［J］.Coastal Engineering，1992，17（3－4）：153－171.

［13］ 李曉亮.斜向和多向不規則波在斜坡堤上越浪量的研究［D］.大連：大連理工大學，2008.LI Xiao－liang.The study of overtopping on sloping seawall under oblique and multidirectional irregular waves ［D］.Dalian： Dalian University of Technology，2008.（in Chinese）

［14］ De Rouck J，Verhaeghe H，Geeraerts J.Crest level assessment of coastal structures — General overview ［J］.Coastal Engineering，2009，56：99－107.

［15］ Pullen T，Allsop N W H，Bruce T，etal.EurOtop：Wave Overtopping of Sea Defences and Related Structures －Assessment Manual ［M］.Hamburg：Kommissionsverlag，2007.

［16］ 楊運澤.模型比尺對塊體穩定性及斜坡堤水力特性的影響［J］.港口工程，1995（1）：17－24.YANG Yun－ze.The model scale effects on the stability of armor blocks and hydraulic characteristics of breakwater［J］.Port Engineering，1995（1）：17－24.（in Chinese）

［17］ Ahrens J P.Irregular Wave Run－up on Smooth Slopes ［M］.Fort Belvoir：National Technical Information Services，Operations Division，1981.

［18］ Stoa P N.Reanalysis of Wave Run－up on Structures and Beaches［M］.Fort Belvoir：National Technical Information Services，Operations Division，1978.

［19］ Stoa P N.Revised Wave Run－up Curves for Smooth Slopes ［M］.Fort Belvoir：National Technical Information Services，Operations Division，1978.