考慮群樁相互作用的層狀地基沉降研究

劉 蕓 李鏡培 鐘光玉

(1．同濟大學地下建筑與工程系，上海20092;2．巖土及地下工程教育部重點實驗室(同濟大學)，上海200092;3．上海南匯建工建設(集團)有限公司，上海201399)

1 引言

群樁基礎由于其承載力高、沉降小、制作靈活方便和適用條件廣泛等諸多優點，在大型橋梁及城市高層建筑基礎建設中得到了廣泛的應用［1］。然而，在上部荷載作用下群樁的沉降性狀會直接影響到上部建筑的安全與穩定。由于群樁受力沉降受樁－樁、樁－土、荷載、樁型及土體性質等眾多因素的影響，其在上部荷載作用下的受力變形機理較為復雜。因此，如何準確合理地確定群樁相互作用系數，分析群樁的沉降機理，并提出群樁沉降的計算方法，具有十分重要的理論研究和現實意義。

目前，群樁間相互作用及沉降研究主要采用以下解析方法:Poulos［2］基于彈性疊加原理，引入群樁相互作用系數，將彈性介質兩根樁的計算結果按相互作用系數方法擴展至群樁，提出了群樁沉降的彈性算法。由于此方法力學概念簡單、操作性強，在實際工程中得到了廣泛的應用。Randolph［3－4］將單樁和樁帽分開考慮，考慮了樁筏相互作用系數來對樁筏基礎的剛度影響，在此基礎上提出了群樁下的樁筏基礎沉降的計算方法。閆綱麗等［5］利用剪切位移法，引入樁－樁相互作用模型，提出了群樁相互作用系數的簡單計算方法，但僅限于群樁處于均質土中。董建國和趙錫宏［6］通過修正函數對理論相互作用系數進行修正，但是修正函數的確定過于依賴工程實測資料，具有一定的局限性。陳云敏［7］將群樁中每根樁的樁頂沉降分成樁身壓縮和樁端沉降兩部分，樁身壓縮由單樁靜載荷試驗或其他方法估算，樁端沉降根據分層總和法計算，提出了一種考慮土－樁－筏相互作用的樁筏基礎簡化分析法。趙明華等［8－9］以荷載傳遞法推導出樁周土的位移場，疊加各樁引起的附加位移，通過修正Boussinesq解得到樁端土剛度系數矩陣，在此基礎上提出了一種群樁沉降計算的方法。此外部分學者采用有限元法和邊界元法對群樁的受荷沉降問題進行了詳細的研究，但計算較為繁瑣，也難于從機理上反映群樁沉降問題的本質。

通過以上文獻可以看出，以往對群樁沉降問題的研究多集中于均質地層，地基土的分層特性、群樁的加筋效應和遮簾效應都沒有得到良好的反映。針對這一問題，本文在充分考慮群樁“加筋效應”和“遮簾效應”的基礎上，根據剪切位移法提出了群樁相互作用系數的簡便算法，并建立了相應群樁沉降的計算公式。本文對完善層狀地基沉降計算理論及群樁設計都具有重要意義。

2 相互作用系數αij的推導

Poulos等［2］在分析幾何形狀、尺寸和受荷狀態完全相同的兩樁組成的群樁時，引入相互作用系數 αij，其定義為

因此，根據疊加原理，群樁沉降公式可寫為

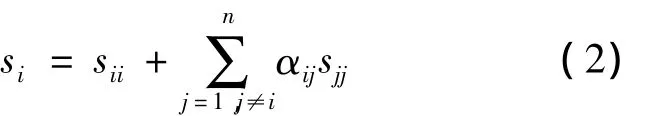
式中，sii為自身樁頂荷載下產生的沉降;sjj為鄰樁樁頂荷載作用下產生的沉降。

由式(2)可知，相互作用系數計算的合理與否直接影響群樁沉降計算的精度。較多理論在計算時，僅考慮群樁處于均質土中，不考慮地基土的分層，因此過高地估計樁與樁之間的相互影響，或者提出的公式不利于計算。因此，筆者在剪切位移法的基礎之上，提出一種考慮樁的“加筋效應”和“遮簾效應”且計算簡便的計算αij的方法，利于方便準確地計算群樁沉降。

2．1 單樁沉降分析

根據彈性理論和軸對程可以得到地表下任一深度z處樁的豎向位移滿足方程:

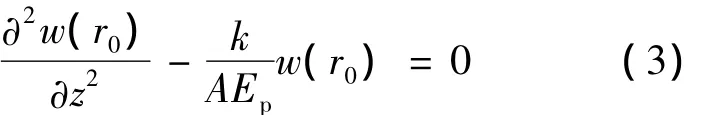
式中，Ep為樁身彈性模量;w(r0)為樁沿深度方向的位移;A為樁身截面積;r0為樁的半徑;k=2πG/ln(rm/r0);rm=2．5Lρm(1 － ν);L 為樁長;ν為土的泊松比。

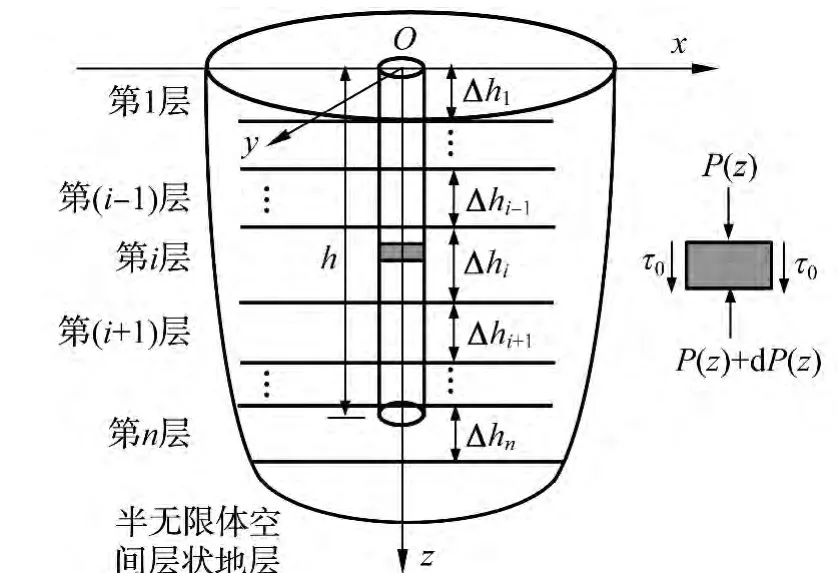
圖1 荷載傳遞法計算圖式Fig．1 Load transfer analysis model

在層狀地基有限深度內，將樁分為n段，則ρm表達式為

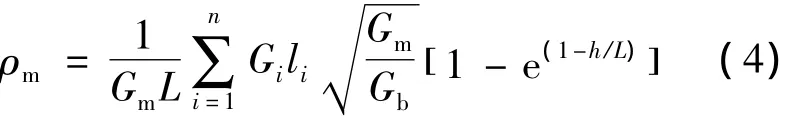
式中，Gm為土的最大的剪切模量;li為單元i的厚度;Gi為單元i土的剪切模量;Gb為樁端土的剪切模量;h為樁端至剛性層的距離。

若討論長度為L的樁段，按土層分為n段，依次遞推可以得到樁頂位移與樁頂軸力之間的關系:

式中，wb為樁端位移;pb為樁端荷載;Gb和ν分別為樁端土的剪切模量和泊松比。

2．2 兩樁共同作用分析

如圖2所示，任取其中2樁為例進行分析。其樁身部分位于成層土中，各個基樁的尺寸L，材料彈性模量Ep及入土深度均相同。

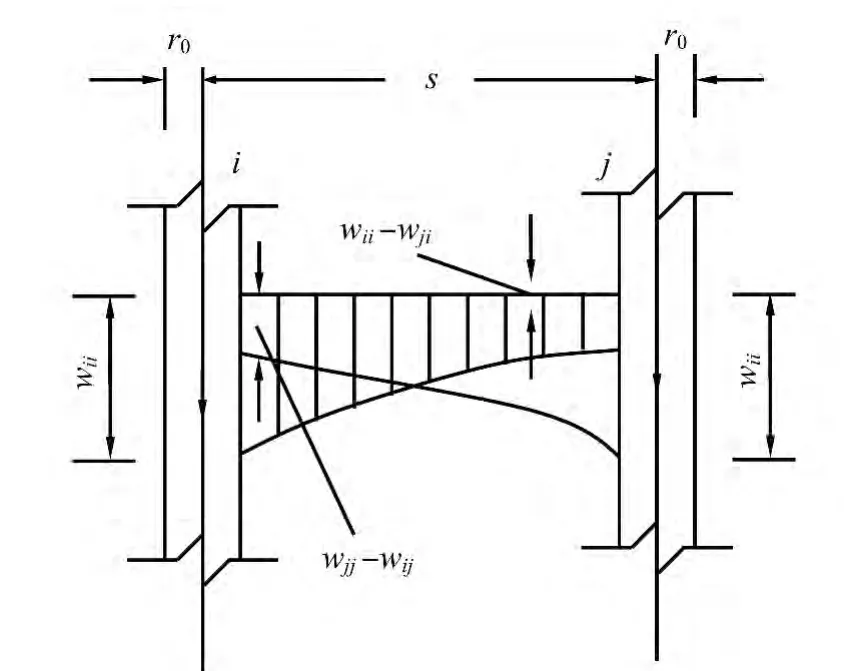
圖2 樁－樁相互作用分析Fig．2 Pile-pile interaction analysis

考慮樁的“遮簾效應”和“加筋效應”，樁i的位移由2個部分組成:樁i在自身荷載下引起的位移wii，以及由于樁的“遮簾效應”和“加筋效應”樁j在自身荷載下引起樁i的位移wij，同理可得樁j的位移組成。即:

若兩根樁的尺寸以及所受荷載都相同，則有:

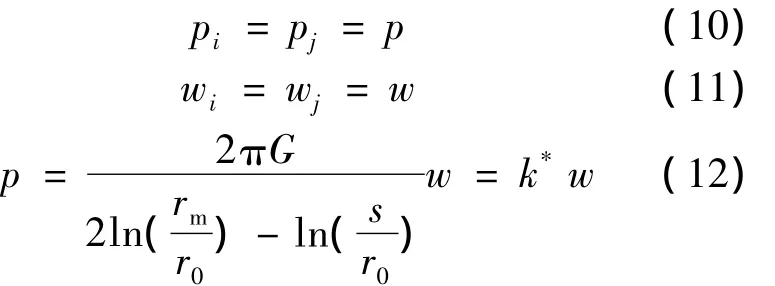
式中:pi，pj分別為i和j樁的樁頂軸力;s為兩樁的中心距;k*為兩根樁共同作用時樁側土的剛度。

2．3 考慮加筋效應和遮簾效應兩樁間相互作用系數推導

設i樁樁端軸力pi=1，可得樁端位移為

由式(5)可得單樁時樁頂軸力pti和位移wti，從而得到在樁頂軸力pti=1時的位移:

再求在j樁的作用下引起的i樁樁頂的位移。兩樁相互作用時，當樁端軸力pi=1時樁i端產生的位移為:

將式(12)中的k*帶入式(5)中，取代k，可得到兩樁相互作用時樁頂位移進而可得考慮兩樁相互作用時，樁i的樁頂軸力=1時的位移

因此可以得到樁j存在時引起的樁i頂部的位移(此時樁i的樁頂軸力=1)為

因此，式(1)的相互作用系數的定義可得:

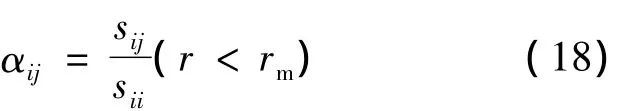
式(18)即為在考慮樁的加筋和遮簾效應時，推導出的層狀地基相互作用系數的具體表達式。

把式(18)代入式(2)，得到考慮樁的“遮簾效應”和“加筋效應”作用時的群樁沉降公式:

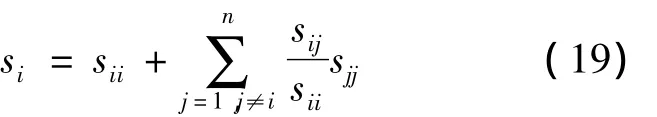
在n根樁組成的群樁中，第i根樁的沉降sii的計算［10］為

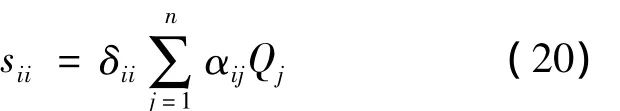
式中，單樁沉降系數δii是單樁在單位荷載下的沉降，它的計算參照文獻［11］;αij=αji，αii=1，本文的計算公式即可計算;Qj為作用在j樁上的荷載。

由于各樁的參數完全相同，剛性承臺中，它們的沉降相同，即:

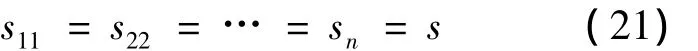
各樁的荷載之和等于總的豎向荷載，即:

聯立式(19)－式(22)即可得到群樁沉降值。

3 群樁沉降算例分析

為了驗證本文算法的合理性以及正確性，選取文獻［12］中上海某馨苑高樓群樁基礎的沉降結果與本文計算結果與進行比較。根據文獻［12］，基礎尺寸為53．4 m ×18．1 m，Φ600 mm 的PHC管樁182根，樁長27 m，樁頂入土深度為5 m，彈性模量為Ep=45 GPa，具體參數及荷載參數見表1。群樁區域內土層分為7層，該工程土層分布條件見表2。

表1 群樁沉降計算參數Table 1 Computation parameters for the group pile settlement

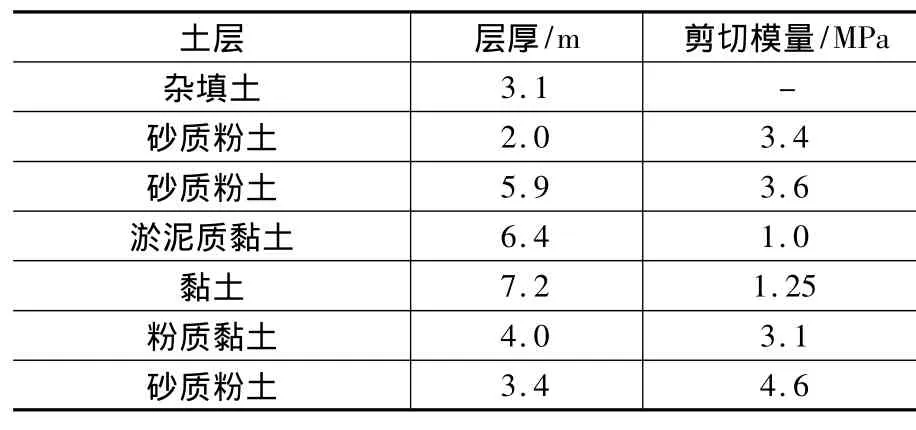
表2 地基土分層特征值Table 2 General characteristic values of layered ground

采用本文提出的方法計算得到的群樁沉降值與實測值的對比情況見表3。

從表3可以看出，某馨苑建成后，群樁實測沉降為37．75 mm，本文方法計算群樁沉降值為30．68 mm，本文計算值與實測值的比值為0．81，與實測值較接近。由于在計算中沒有考慮土體的塑性和非線性，因而計算結果會小于實測值，但總體來講本文計算值其與實測值的差距很小，因而可以應用于對沉降有嚴格要求或者沉降值較小的群樁基礎沉降計算及預測中。

表3 群樁沉降計算值與實測值對比Table 3 Group pile settlement comparison between the measured value and the calculated value

4 相互作用系數的影響因素分析

4．1 與文獻［5］解比較

本文方法得到的相互作用系數和文獻［5］得到的結果進行比較，圖3給出了文獻［5］與本文方法計算4×4群樁(地質條件以及各項參數取與實例相同)相互作用系數的結果。從圖3可以看出地基的非均勻性對相互作用系數的影響很大。非均勻地基中的相互作用系數比均勻地基中文獻［5］計算得到的結果要小很多，這也造成了用傳統方法得到的相互作用系數去計算群樁沉降較實測值偏大的原因之一。

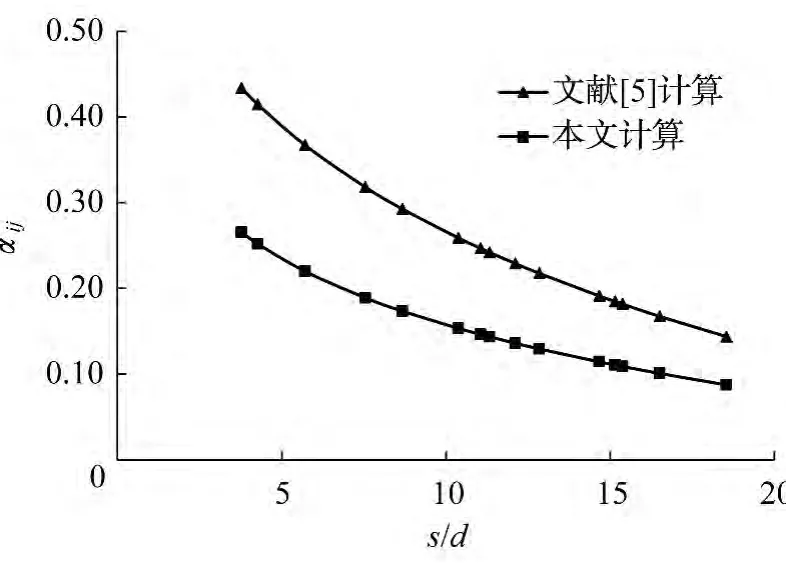
圖3 分層土中相互作用系數Fig．3 Interaction coefficient in layered soil

4．2 群樁相互作用系數的影響分析

以群樁沉降算例為例進行分析。圖4給出了相互作用系數隨樁長細比的變化，圖5給出了相互作用系數隨樁身剛度的變化。

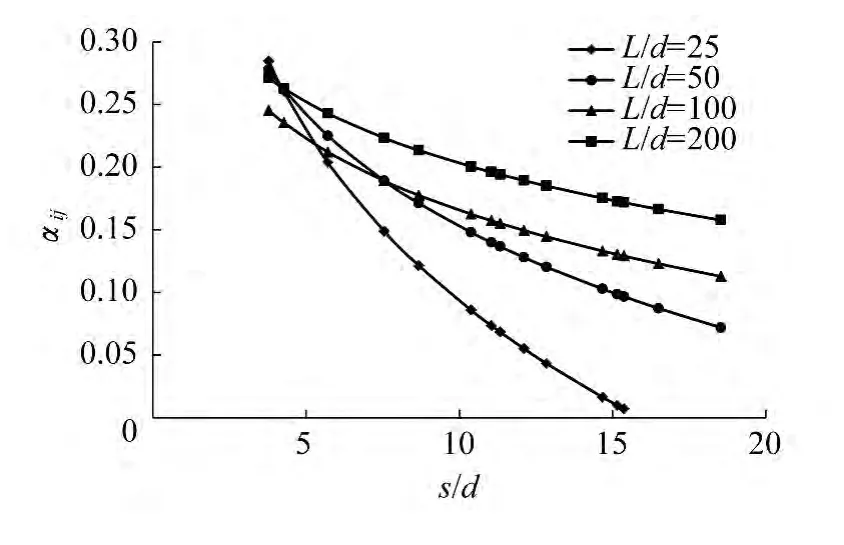
圖4 兩樁的相互作用系數隨樁長細比的變化Fig．4 The interaction coefficients of two piles along with the change of pile slenderness ratios

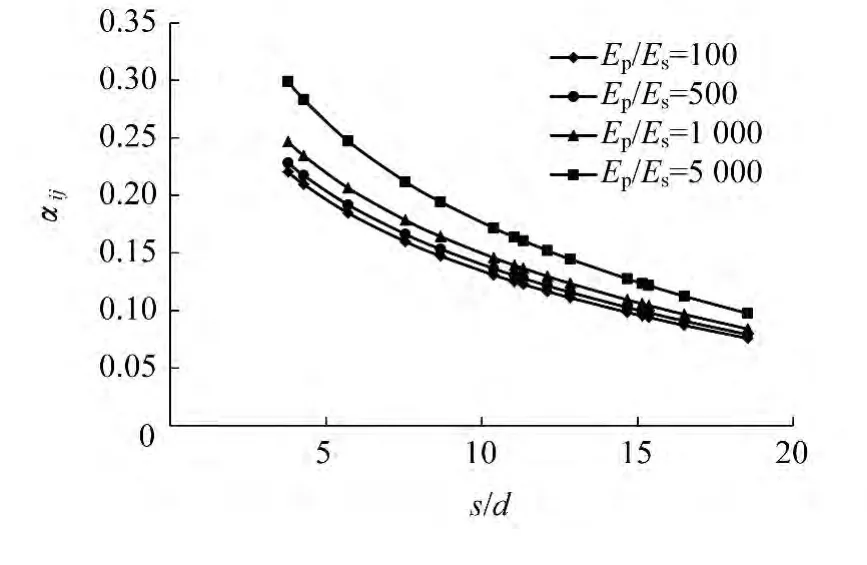
圖5 兩樁的相互作用系數隨樁身剛度的變化Fig．5 Interaction coefficient of two piles along with the change of pile stiffness

分析圖4和圖5可以得到如下規律:

(1)樁的相互作用系數隨著樁間距的增加、樁身剛度的減小或者樁長細比的增加會有所減小。

(2)在圖4中，樁的長細比為L/d=25時已明顯地偏離真實情況，而且在s/d＞16時已無法計算相互作用系數。對此本文的見解為:由于樁的長細比比較小，平面應變假定不能成立。

(3)在圖5中，當樁身的剛度在適中的范圍時(100＜Ep/Es＜5 000)，由于樁的剛度引起的相互作用系數之間的差距較小。

5 結論

針對群樁相互作用系數及沉降問題，根據剪切位移法，考慮土體的成層特性及群樁“遮簾效應”和“加筋效應”，對兩樁間相互作用系數的計算方法進行改進，建立了層狀地基群樁沉降的計算公式，分析了群樁沉降的工程實例。得到的結論如下:

(1)通過推導兩樁相互作用系數，建立群樁沉降的計算公式，該公式也適用于層狀地基。

(2)算例與工程實例分析表明:該方法的計算結果與實測值吻合較好，適用于對沉降有嚴格要求或者沉降值較小的工程。

(3)樁的相互作用系數隨著樁間距的增加而減小，隨樁身剛度的增大而增大，隨樁長細比的增加而減小。

(4)本文方法只適用于等長的群樁，對于群樁中各樁剛度不同的情況并不適應，需要進一步研究與發現。

［1］ 薛亮．橋梁樁基礎計算機輔助分析設計系統［D］．成都:西南交通大學，2007:4-5．Xue Liang．Computer-aided analysis and design of bridge pile foundation［D］．Chengdu:Southwest Jiaotong University，2007:4-5．(in Chinese)

［2］ Poulos H G，Davis E H．Pile foundation analysis and design［M］．New York:John Wiley and Sons，1980．

［3］ Randoplh M F．Design methods for pile groups and piled rafts［R］．S．O．A．Report，13ICSMFE，New Delhi，1994，5:61-82．

［4］ Randoplh M F．Design of piled foundaitions［R］．Cambridge Univ． Eng． Dept．，Res． Rep． soils TR143，1983．

［5］ 閆綱麗，張紅芬．群樁間相互作用系數計算［J］．華東水利水電學院學報，2011，32(3):93-95．Yan Gangli，Zhang Hongfen．Interaction coefficient between the pile group［J］．Journal of East China Water Conservancy and Hydropower College，2011，32(3):93-95．(in Chinese)

［6］ 董建國，趙錫宏．高層建筑地基基礎-共同作用理論與實踐［M］．上海:同濟大學出版社，1997．Dong Jianguo，Zhao Xihong．High-rise building foundation base-interaction theory and practice［M］．Shanghai:Tongji University Press，1997．(in Chinese)

［7］ 陳云敏，陳仁朋．考慮相互作用的樁筏基礎簡化分析方法［J］．巖土工程學報，2001，23(6):686-691．Chen Yunmin，Chen Renpeng．Simplified analysis method considering the interaction of pile raft foundation［J］．Geotechnical Engineering，2001，23(6):686-691．(in Chinese)

［8］ 趙明華，鄒丹，鄒新軍，等．群樁沉降計算的荷載傳遞法［J］．工程力學，2006，23(7):119-123．Zhao Minghua，Zou Dan，Zou Xinhua，et al．Load transfer method of pile group settlement calculation．［J］．Engineering Mechanics，2006，23(7):119-123．(in Chinese)

［9］ 趙明華，鄒丹，部新軍，等．基于荷載傳遞法的高承臺樁基沉降計算方法研究［J］．巖石力學與工程學報，2005，24(13):2310-2314．(in Chinese)Zhao Minghua，Zou Dan，Bu Xinjun，et al．High pile caps foundation settlement based on the load transfer method［J］．Rock Mechanics and Engineering，2005，24(13):2310-2314．

［10］ 劉金礪，黃強，李華，等．豎向荷載下群樁變形性狀及沉降計算［J］．巖土工程學報，1990:1-13．Liu Jinli，Huang Qiang，Li Hua，et al．Pile groups deformation behavior and the settlement under vertical load［J］．Geotechnical Engineering，1990:1-13．(in Chinese)

［11］ 朱百里，沈珠江．計算土力學［M］．上海:上海科學技術出版社，1995，17(6):233-267．Zhu Baili，Shen Zhujiang．Calculation of soil mechanics［M］．Shanghai:Shanghai Science and Technology Press，1995，17(6):233-267．(in Chinese)

［12］ 楊敏，王偉．群樁沉降計算的試樁曲線法［J］．結構工程師，2008，24(5):77-88．Yang Min，WangWei．Calculation method of pile group settlement based on static load test curves［J］．Structural Engineers，2008，24(5):77-87．(in Chinese)