基于最小二乘法的感應電能無線傳輸系統負載辨識方法

蘇玉剛 陳 龍 王智慧 呼愛國 戴 欣

(1.重慶大學自動化學院 重慶 400030 2.奧克蘭大學電子與計算機工程系 奧克蘭 1010)

?

基于最小二乘法的感應電能無線傳輸系統負載辨識方法

蘇玉剛1陳 龍1王智慧1呼愛國2戴 欣1

(1.重慶大學自動化學院 重慶 400030 2.奧克蘭大學電子與計算機工程系 奧克蘭 1010)

基于最小二乘法提出一種新型負載辨識方法，以PS結構電流型感應電能傳輸(IPT)系統為例，建立其非線性高階微分方程并構建數據矩陣，通過最小二乘法獲得系統的過程參數矢量，將負載辨識問題轉換為系統參數辨識問題，完成系統的負載辨識，最后通過仿真及實驗，驗證了此方法的可行性。

感應電能傳輸(IPT) 最小二乘法 參數辨識

0 引言

感應電能傳輸(Inductive Power Transfer，IPT)技術是一種借助時變電磁場將電能從電源端耦合到負載端的電能傳輸新技術[1，2]。IPT技術理論及其關鍵技術的深入研究，推動了IPT技術在電動車充電、電子產品充電、生物醫電以及照明系統等諸多領域的廣泛應用[3-9]。

在某些實際應用中(例如廚房家電)，能量拾取裝置按要求放置于能量發射平臺上，且發射線圈與拾取線圈之間距離固定，此情況下可將互感近似視為定值，但負載的改變無法避免。由于系統負載的變化，源自能量接收端(二次電路)的反射阻抗會在能量發射端(一次電路)具有相應變化，使得一次電路的固有頻率發生漂移[10]，從而不再與工作頻率匹配。這將導致系統偏離軟開關工作點，從而影響系統的功率傳輸能力，增加開關損耗及電磁干擾(EMI)[11]。此外，當負載變化，系統需根據當前負載情況調整能量發射端的控制模式，實現系統的最佳效率跟蹤控制，負載辨識是其關鍵問題。因此，為了建立更加高效、可靠、穩定的IPT系統，負載的辨識問題亟待解決。然而，系統的高階非線性使得負載辨識問題成為一個技術瓶頸。針對上述問題，文獻[12-14]基于系統的能量模型，從能量守恒角度建立方程，完成對負載的辨識。文獻[15]在初始時刻給系統注入能量，隨后使其自由振蕩，通過推導出一次電流衰減率與負載之間的關系完成負載辨識，但不是一種穩態下的負載辨識策略。

本文基于最小二乘法提出一種新型的負載辨識策略。以PS結構的電流型IPT系統為例，通過建立系統非線性高階微分方程完成對數據矩陣的構建，并在此基礎上利用最小二乘法完成對系統過程參數的辨識，通過過程參數矢量及負載間的線性關系完成對負載的辨識，將直接對負載辨識的問題轉換為對系統參數辨識的問題。最后通過仿真分析及實驗驗證了此方法的可行性，且具有一定準確度，是一種易實現的負載辨識方法。

1 主電路拓撲

圖1給出了較常見的PS結構電流型IPT系統。該系統由一次電路及二次電路兩個獨立部分所組成。在一次側部分，直流電壓源Edc提供整個系統的電能輸入，Ldc為濾波電感，Edc與Ldc串聯可近似視為電流源并在穩態時產生近似恒定電流idc。開關管S1～S4構成一次高頻逆變電路，兩組開關管(S1，S4)及(S2，S3)輪流導通將DC激勵電流idc逆變為高頻方波電流iac，一次電容Cp、一次繞組Lp構成一次并聯諧振電路；在二次側部分，二次電容Cs、二次繞組Ls構成二次串聯諧振電路，二級管VD1～VD4及濾波電容C構成二次整流電路，將高頻交流電壓轉換為電壓uo作用于負載RL上。其中，M為耦合電感Lp、Ls之間互感，Rp、Rs分別為電感Lp、Ls串聯等效電阻。

對于一次電路，電壓源Edc產生直流電壓流經濾波電感Ldc，通過高頻逆變電路后輸出近似方波的電流iac；對于二次電路，帶有濾波電容C的整流電路與負載RL并聯時可等效為負載Req，等效負載Req的阻抗由

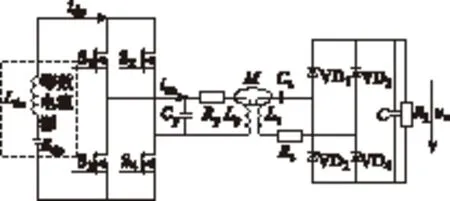
圖1 基于PS型IPT系統主電路拓撲Fig.1 The main circuit of a PS-type IPT system

Req=(8/π2)RL≈0.81RL

(1)

因此可得到主電路的等效電路，如圖2所示。其中，iac為一次逆變器輸出方波電流，up為一次諧振電容Cp端電壓，ip為一次繞組諧振電流，us為二次諧振電容Cs端電壓，is為二次繞組諧振電流，R1為電阻Req、Rs串聯等效電阻，即

R1=Req+Rs

(2)

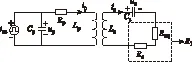
圖2 基于PS型IPT系統的等效電路圖Fig.2 The equivalent circuit of PS-type IPT system

2 IPT系統負載辨識

2.1 基于最小二乘法的參數辨識

對于上述IPT系統，可獲得如下形式的差分方程

z(k)+a1z(k-1)+…+amz(k-m)=

b1u(k)+…+bn+1u(k-n)

(3)

由于k存在一系列取值，因此可進一步將式(3)改寫為矩陣形式

ZL=HLθ

(4)

其中

(5)

(6)

(7)

式中，ΗL為系統數據矩陣；L為數據長度。

當負荷功率分別為2 MVA、4 MVA、6 MVA，功率因數為0.85，XC=0時，串補裝置處節點電壓分別為9.57 kV、8.89 kV、8.19 kV，若加入補償度k=2.25的補償電容時，補償點電壓分別提升1.272 kV、1.591 kV、1.668 kV。結果如圖4所示：容量與電流的平方成正比，而串聯電容器補償的電壓與線路電流成正比。因此，當線路容量增大時，電流增大，補償的電壓也隨之增大。這就是串補的負荷自適應特性，也是其他無功補償均不具備的特性。

顯然，可通過最小二乘法，得到過程參數矢量θ的最小二乘估計

(8)

2.2 IPT系統數據矩陣構建及負載辨識

為了獲得IPT系統的過程參數矢量及數據矩陣，首先建立系統非線性微分方程。

由圖2所示的等效電路圖，構建如下方程

(9)

選取一次逆變器輸出方波電流iac及一次繞組電流ip作為考慮的狀態變量。將式(9)進行Laplace變換可得到Iac(s)、Ip(s)之間的關系為

(a1s4+a2s3+a3s2+a4s+a5)Ip(s)=

(b1s2+b2s+b3)Iac(s)

(10)

進而獲得如下傳遞函數

(11)

其中

(12)

(13)

為了獲得更為精準的系統離散模型，經過分析比較，選用Tustin法對式(11)進行離散化處理。處理后得到如下關系式(Iac(z)、Ip(z)分別為iac、ip的Z變換)

(14)

其中

(15)

(16)

式中，c=2/T，T為采樣周期。

將式(14)進行反變換可構建出IPT系統的一組差分方程

(17)

最終可得到IPT系統的數據矩陣及過程參數矢量

(18)

(19)

(20)

3 仿真分析及實驗驗證

為了驗證本文提出的負載辨識方法，基于Matlab/Simulink仿真平臺建立系統仿真模型，并基于主電路拓撲搭建實驗系統，其中一、二次諧振回路的主要參數見表1。

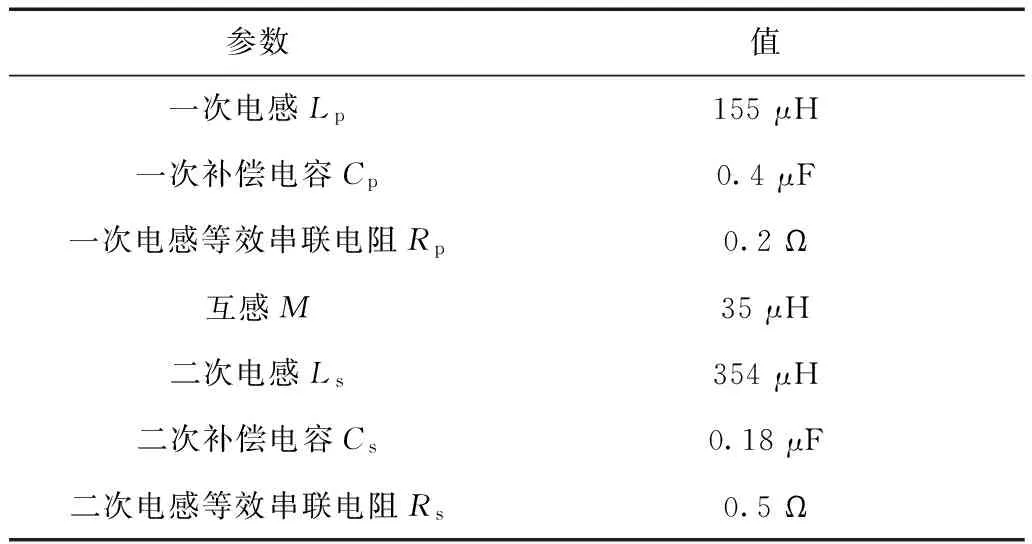
表1 IPT系統仿真及實驗參數Tab.1 Parameters of IPT System

以負載大小為30 Ω及50 Ω的情況為例進行仿真及實驗驗證。圖3、圖4分別給出逆變器輸出電流iac及諧振電流ip的仿真波形及實驗波形。可以看出，iac為近似交變方波，ip為正弦波，與圖2的分析結果一致。在負載大小為30 Ω、50 Ω的情況下，對圖3、圖4中所示的狀態變量iac、ip進行采樣，分別進行50次辨識。為了簡化計算，通常將數據矩陣構建為方陣，因此這里數據長度L取值為9。

為了便于對比，圖5a、圖5b分別給出了負載值為30 Ω、50 Ω時50次仿真及實驗負載辨識結果的統計圖。由圖5可得出，當負載值為30 Ω時，仿真結果中誤差率在5%以內的占97%，相對的，實驗結果誤差較大，其誤差率在5%以內的辨識結果占91%；當負載值為50 Ω時，仿真結果和實驗結果誤差率在5%以內的比例分別為94%及88%。

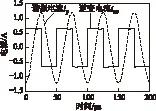
圖3 一次諧振電流及逆變電流仿真波形Fig.3 Simulation waveforms of resonant current and inverter current in the primary side

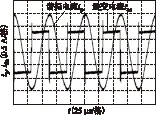
圖4 一次諧振電流及逆變電流實驗波形Fig.4 Experimental waveforms of resonant current and inverter current in the primary side

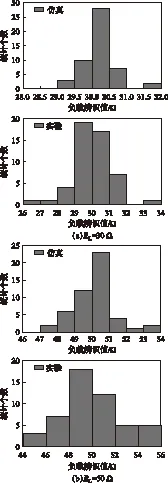
圖5 負載辨識結果分布Fig.5 Distributing of load detection results

為了更直觀地表明辨識準確度的平均水平，表2進一步給出了上文獲得的負載辨識仿真及實驗結果的數據分析。

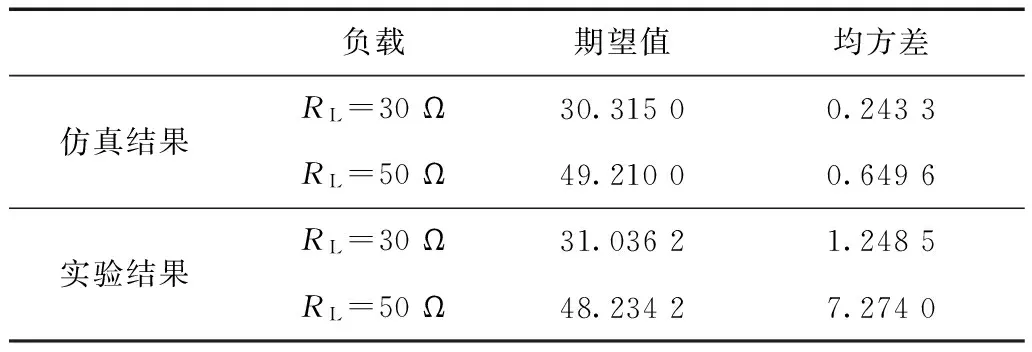
表2 負載辨識結果分析Tab.2 Results analysis of system

由表2可知，當負載RL分別為30 Ω和50 Ω時，仿真得到負載辨識結果期望值的誤差率分別為1.05%和1.58%，實驗得到負載辨識結果期望值的誤差率分別為3.45%和3.53%。因此，在多次辨識后，對得到的數據進行分析，并取其期望值作為最終負載辨識結果能顯著提高結果的準確度。另外，通過圖5及表2可看出實驗結果的分布區間較寬、總體均方差較大、辨識結果誤差較大，這是由于噪聲干擾、實驗儀器的誤差及算法存在一定誤差等原因造成。

顯然，辨識次數與辨識結果的誤差率之間存在一定規律，在實際應用中應根據不同情況選擇不同的辨識次數。圖6通過仿真給出了當負載RL分別為30 Ω及50 Ω時，辨識次數與負載辨識結果誤差率之間的規律。

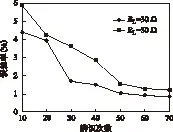
圖6 負載辨識結果誤差率比較Fig.6 Error rates comparisons

從圖6可看出，隨著辨識次數的增加，誤差率逐漸下降。值得注意的是，當辨識次數達到50次時，誤差率下降曲線逐漸平滑。因此，在實際應用中如需較高的辨識準確度，辨識次數選擇50次即可滿足，繼續增加辨識次數不但不再使誤差率有顯著下降，反而會增加計算成本，影響辨識的實時性。相反，如需較快的辨識速度，可根據實際情況降低辨識次數，當然這樣也會相應的降低辨識準確度。

4 結論

本文通過對感應式無線電能傳輸系統建模分析，完成其數據矩陣的構建，并以此為基礎利用最小二乘法完成負載辨識。針對系統運行中因負載變化而增大系統控制難度的問題，提出一種實時的負載辨識方法。仿真及實驗結果表明該辨識方法具有較高準確度，并通過仿真給出了辨識次數和辨識結果誤差率之間的關系。該方法對于其他結構類型IPT系統的負載辨識具有參考價值。

[1] 黃學良，譚林林，陳中，等.無線電能傳輸技術研究與應用綜述[J].電工技術學報，2013，28(10)：1-11. Huang Xueliang，Tan Linlin，Chen Zhong，et al.Review and research progress on wireless power transfer technology[J].Transactions of China Electrotechnical Society，2013，28(10)：1-11.

[2] Covic G A，Boys J T.Inductive power transfer[J].Proceedings of the IEEE，2013，101(6SI)：1276-1289.

[3] Hui S Y R，Ho W W C.A new generation of universal contactless battery charging platform for portable consumer electronic equipment[J].IEEE Transactions on Power Electronics，2005，20(3)：620-627.

[4] Si Ping，Hu A P，Malpas S，et al.A frequency control method for regulating wireless power to implantable devices[J].IEEE Transactions on Biomedical Circuits and Systems，2008，2(1)：22-29.

[5] 周煜，于歆杰，程錦閩，等.用于心臟起搏器的經皮能量傳輸系統[J].電工技術學報，2010，25(3)：48-53. Zhou Yu，Yu Xinjie，Cheng Jinmin，et al.Transcutaneous energy transmission system for cardiac pacemaker[J].Transactions of China Electrotechnical Society，2010，25(3)：48-53.

[6] James Jason E I，Chu Alex，Robertson Daniel，et al.A series tuned high power IPT stage lighting controller[C].IEEE Energy Conversion Congress and Exposition，Phoenix，AZ，2011：2843-2849.

[7] Robertson D，Chu A，Sabitov A，et al.High power IPT stage lighting controller[C].IEEE International Symposium on Industrial Electronics (ISIE)，Gdansk，2011：1974-1979.

[8] 曹玲玲，陳乾宏，任小永，等.電動汽車高效率無線充電技術的研究進展[J].電工技術學報，2012，27(8)：1-13. Cao Lingling，Chen Qianhong，Ren Xiaoyong，et al.Review of the efficient wireless power transmission technique for electric vehicles[J].Transactions of China Electrotechnical Society，2012，27(8)：1-13.

[9] Budhia M，Boys J T，Covic G A，et al.Development of a single-sided flux magnetic coupler for electric vehicle IPT charging systems[J].IEEE Transactions on Industrial Electronics，2013，60(1)：318-328.

[10]Wang Chwei-Sen，Covic G A，Stielau O H.Power transfer capability and bifurcation phenomena of loosely coupled inductive power transfer systems[J].IEEE Transactions on Industrial Electronics，2004，51(1)：148-157.

[11]唐春森，孫躍，戴欣，等.感應電能傳輸系統多諧振點及其自治振蕩穩定性分析[J].物理學報，2011，60(4)：745-753. Tang Chunsen，Sun Yue，Dai Xin，et al.Analysis of multiple resonant operating points and their autonomous oscillation stabilities in inductive power transfer systems[J].Acta Physica Sinica，2011，60(4)：745-753.

[12]Dai Xin，Sun Yue，Tang Chunsen，et al.Dynamic parameters identification method for inductively coupled power transfer system[C].IEEE International Conference on Sustainable Energy Technologies，Kandy，2010：1-5.

[13]戴欣，王智慧，唐春森，等.感應電能傳輸系統參數辨識與恒流控制[J].重慶大學學報，2011，34(6)：98-104. Dai Xin，Wang Zhihui，Tang Chunsen，et al.Study on constant current control of in ductive power transfer with parameter identification[J].Journal of Chongqing University，2011，34(6)：98-104.

[14]Wang Zhihui，Lv Xiao，Sun Yue，et al.A simple approach for load identification in current-fed inductive power transfer system[C].IEEE International Conference on Power System Technology，Auckland，2012：1-5.

[15]Wang Zhihui，Li Yupeng，Sun Yue，et al.Load detection model of voltage-fed inductive power transfer system[J].IEEE Transactions on Power Electronics，2013，28(11)：5233-5243.

A Load Identification Method for Inductive Power Transfer System Based on the Least Squares Algorithm

SuYugang1ChenLong1WangZhihui1AiguoPatrickHu2DaiXin1

(1.Automation college of Chongqing University Chongqing 400030 China 2.Department of Engineering The University of Auckland Auckland 1010 New Zealand)

Identifying load parameters is essential to establishing an efficient，reliable and stable inductive power transfer (IPT) system.Additionally，it is the key problem to achieve optimal efficiency tracking control.This paper focuses on the parallel-serial-(PS)-type current-fed IPT system and the data matrix can be constructed by setting up high order nonlinear differential equations of the system.The load identification problem is then transformed in to the system parameter identification problem，which is solved by the acquisition of the system process parameters vector based on the least squares algorithm.Finally，the simulations and the experiments can verify the feasibility of the proposed method.

Inductive power transfer，least squares algorithm，load identification

國家自然科學基金(51477020，51377183)和國家自然科學青年基金(51207173)資助項目。

2014-11-06 改稿日期2015-01-10

TM724

蘇玉剛 男，1962年生，博士，教授，研究方向為無線電能傳輸技術、電力電子技術、控制理論應用與自動化系統集成。(通信作者)

陳 龍 男，1989年生，博士研究生，研究方向為電力電子技術和無線電能傳輸技術。