基于Weibull 時間序列函數與負指數法的動態沉陷預計

王小華 胡海峰 廉旭剛

(太原理工大學礦業工程學院，山西 太原030024)

研究開采沉陷動態過程對于預防沉陷災害的發生具有重要的實用價值，對此，Knothe［1］于1952 年提出了Knothe 時間函數模型，但經實踐證明該模型不符合地表下沉的客觀過程;常占強等［2］假設地表觀測點的沉陷速度在整個沉陷過程的中間時刻最大，將沉陷過程劃分為前后對稱的2 個過程，采用對加速和減速階段分別建模的方法改進了Knothe 時間函數，但基于該對稱假設建立的模型不完全符合實際情況;徐洪鐘等［3］采用了Logistic 曲線研究地表下沉的動態過程，但該曲線模型為生物增長模型，其增長量的增加應有一定的基數基礎，同時該模型求出的下沉速度和加速度在初始時刻均不為0，這顯然不符合開采引起的地表沉陷的客觀規律。一些學者也從不同的角度研究了描述地表沉陷區觀測點下沉量的時間序列函數［4-6］，但該函數模型描述的地表下沉不完全符合地表沉陷的客觀過程;劉玉成等［7-8］分別從下沉曲線形狀、下沉速度和加速度3 個方面比較分析了現有的各類時間函數模型對描述地表沉陷過程的適應性，指出只有Weibull 時間序列函數能夠完整描述地表沉陷的動態過程，并基于該函數建立了地表沉陷的動態概率積分模型。在各類開采沉陷預計模型中，負指數法因其預計參數通常表示為與地質采礦條件數據有關的經驗公式，函數形式直接根據實測資料選定，使得預計結果更接近地表沉陷的真實狀況，在表示對于拐點不呈反對稱的實際下沉曲線方面具有更大的靈活性［9］。為此，在充分研究采場上覆巖層破斷特征［10-12］及工作面停采后地表移動變形規律［13-17］的基礎上，將Weibull 時間序列函數與負指數沉陷函數相結合，建立充分采動條件下走向主斷面的動態地表移動變形模型，研究開采沉陷的動態過程。

1 建模理論基礎

1.1 Weibull 時間序列函數

采用Weibull 曲線函數描述地表沉陷區某觀測點下沉量與時間的關系，表達式為

式中，Wm為地表沉陷區觀測點沉陷穩定后的最大下沉量，mm;n1為與采空區上覆巖層性質有關的參數，決定地表觀測點下沉過程的時間長短;t 為觀測點下沉所用的時間，d;k 為與采空區上覆巖層性質有關的參數，決定地表觀測點在下沉過程中時間軸上的運動路徑，可由下沉速度和加速度的變化規律體現。參數n1、k 可通過最小二乘法擬合確定。

對式(1)計算一階和二階導數分別得到地表觀測點下沉速度v(t)和加速度a(t)的函數表達式

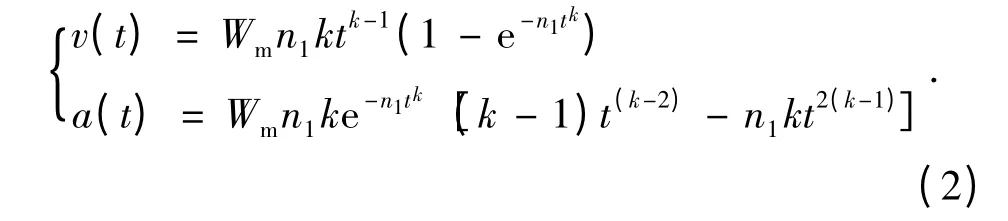
文獻［7］通過分析得出Weibull 函數曲線大致呈“S”型，能有效描述地表沉陷有限增長的動態過程，且下沉速度的變化過程為0 →vmax→0 ，加速度的變化過程為0 →+amax→0 →－amax→0 ，均與地表沉陷的物理過程相符合。

1.2 走向主斷面半無限開采負指數法下沉預計公式

地表下沉盆地穩定后，走向半無限開采的負指數法下沉預計公式為［18］

式中，Cym為沿走向的采動程度系數;H 為煤層采深，m;W0為充分采動條件下地表的最大下沉值，mm;a，n，c 為負指數法的特定參數，a 為橫向發育系數，n 為形態系數，c 為最大下沉點的位置系數。

式(3)中參數a，n，c 可按照文獻［19］給出的3種方法(最小二乘法、圖解法和電算法)求取，若缺乏實測地表移動觀測資料，可按照類比法并參照礦區已有的相關資料選取參數。煤層上覆巖層中硬條件下負指數法的有關預測參數見表1。

表1 中硬巖層條件下模型的預測參數值Table 1 Model prediction parameter values of medium hard rock strata

2 地表沉陷動態負指數法預計模型

2.1 主斷面動態沉陷模型的一般形式

地表沉陷盆地內觀測點的下沉變化過程在時間和空間上是相對獨立的，表現在剖面線上任意點在時間軸上的下沉過程以及整條剖面線在空間軸的下沉過程具有相對獨立性［20］。因此地表沉陷盆地主斷面上的動態下沉計算模型可定義為

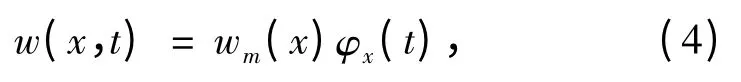
式中，wm(x)為地表沉陷盆地穩定后主斷面的下沉曲線函數;φx(t)為地表沉陷盆地主斷面上任意x 點的下沉時間序列函數。

文獻［21］通過采用FLAC3D軟件模擬煤層的連續開采過程，并結合地表沉陷結果，得出了在相同的開采條件和過程中，地表沉陷盆地主斷面任意2 點的下沉過程在時間上具有相同的運動規律。因此沉陷盆地主斷面上的所有觀測點下沉時間序列可用函數φ(t)來表示，即φ(t)= φx(t)，于是，地表沉陷盆地主斷面的動態下沉模型可表示為

2.2 充分采動走向主斷面動態負指數法預計模型

走向主斷面在充分采動條件下，隨著工作面的不斷推進，下沉曲線也向前移動，其位置關系見圖1(l0為超前影響距離，m;ω 為超前影響角，(°);δ0為邊界角，(°))，以工作面開采至P1時的坐標系統為準，設工作面向前推進l 時所用的時間為t。

圖1 下沉曲線隨的位置變化Fig.1 Position change of subsidence curves

當地表下沉盆地穩定后，此時走向半無限開采的負指數法下沉預計公式為

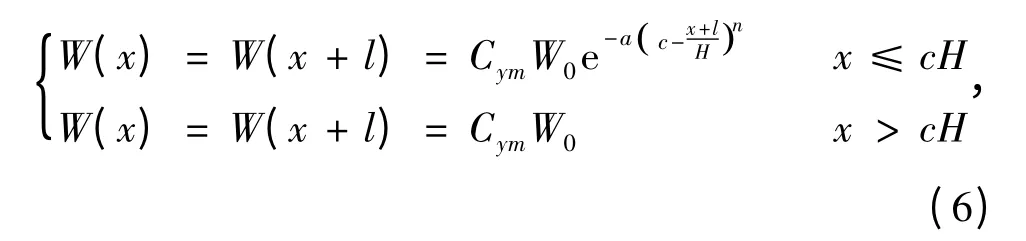
式中，l 為工作面推進距離，m。

將式(4)、式(5)中的主斷面的下沉曲線函數wm(x)用走向半無限開采的負指數法下沉預計公式(式(6))表示，主斷面上所有觀測點下沉的時間序列函數φ(t)用Weibull 時間序列函數(式(1))表示，則可建立充分采動條件下走向主斷面的動態沉陷負指數法下沉預計模型

對(7)式分別計算x 的一階、二階導數，可得到充分采動走向主斷面動態沉陷負指數法傾斜和曲率預計模型

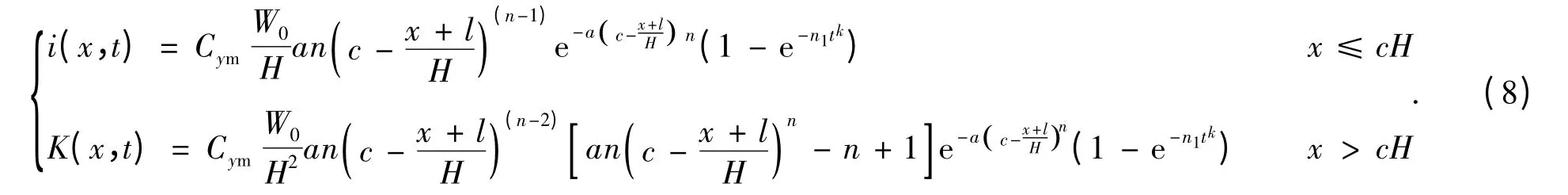
由文獻［19］給出的水平移動、水平變形與傾斜、曲率的關系可得到充分采動走向主斷面動態沉陷負指數法水平移動和水平變形預計模型

3 應用實例

山西某煤礦開采一工作面走向長約1 850 m，傾向長270 m，煤層平均采深約610 m，煤層開采厚3.3 m，煤層傾角約7°。在走向主斷面上方地表距離開切眼約1 260 m 處沿著煤層開采方向設立一走向觀測線，共設觀測點48 個，點間距25 m，沿著工作面推進方向觀測點編號順序為348#，347#，…，301#，隨后在2012 年7 月—2014 年8 月連續進行了21 次觀測。地面沉陷有效觀測點為301#～343#點，對下沉量最大的343#點的各期下沉量采用Weibull 時間序列函數擬合，得到參數n1=0.00 035 mm/d，k =3.11。該工作面上覆巖層多為粉砂巖和泥巖，巖性較軟，且松散層較厚，參考該礦已有的參數資料，綜合選取下沉系數q=0.86，水平移動系數b=0.25，沿走向的采動程度系數Cym=0.94。將最終穩定后的各觀測點數據采用文獻［8］給出的最小二乘法擬合，計算出負指數法的特定參數a=3.6，n=3.1，c=tan30°。

采用圖1 所示坐標系統，下沉10 mm 的343#點即圖1 中的N1點，所對應的的工作面開采位置為P1點。4 期不同的l、t 值所對應的預測曲線見圖2，其中第2 期和第4 期相應觀測點的實測值、預計值及預計誤差見表2。

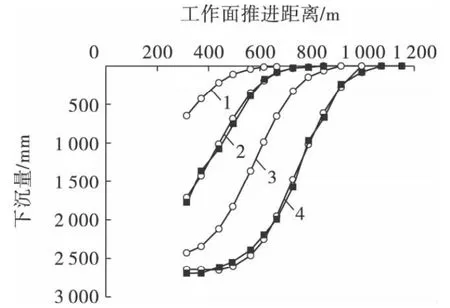
圖2 走向主斷面下沉曲線隨時間變化Fig.2 Main section subsidence curves change with time

由圖2、表2 可知，下沉預計曲線隨時間的變化符合工作面推進過程中地面沉陷的實際過程;第2 期和第4 期的預計曲線與實測曲線形態相近，2 期的最大相對誤差分別為7.3%和2.7%，擬合效果較好。

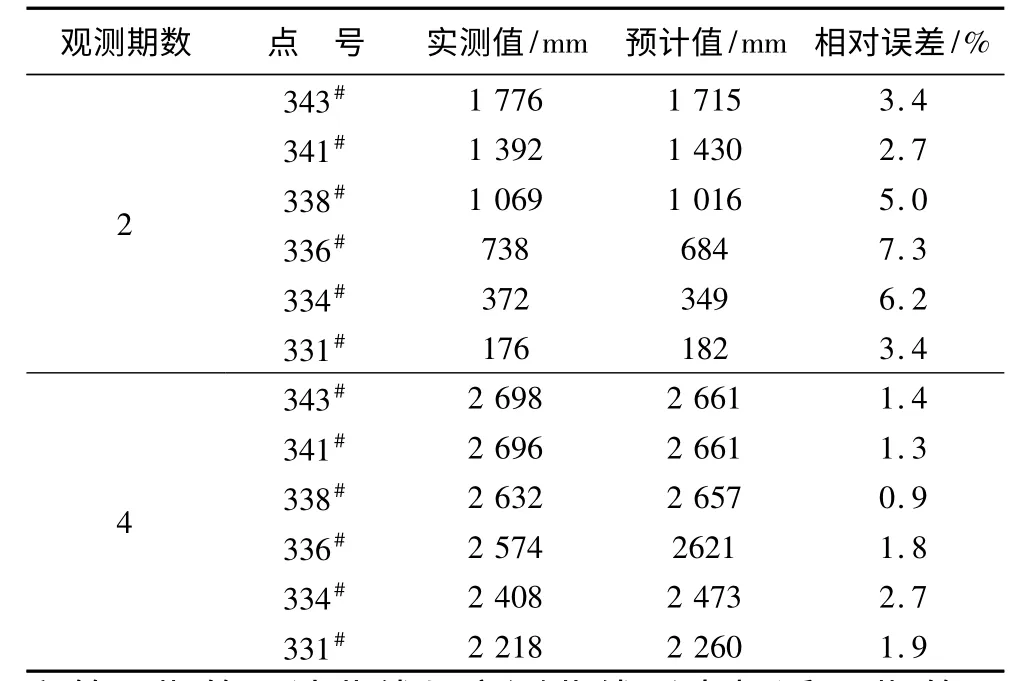
表2 預計誤差Table 2 Prediction error

充分采動走向主斷面動態傾斜、曲率、水平移動和水平變形曲線，見圖3。由圖3 可知，基于Weibull時間序列函數和負指數法的動態沉陷預計模型在一定程度上可描述煤層工作面開采過程中地表沉陷的動態變化過程。

4 結 語

分析了Weibull 時間序列函數描述開采沉陷區觀測點的動態變化過程，并給出了充分采動條件下走向主斷面負指數法的下沉預計公式及參數求取方法。在此基礎上，將Weibull 時間序列函數與負指數法相結合，建立了充分采動條件下走向主斷面動態負指數法預計模型，并進行了實例驗證分析。結果表明，該模型的地表動態沉陷預測結果與實際觀測值的誤差較小，從而證明了該模型的有效性。

圖3 4 類曲線隨時間的變化Fig.3 Four kinds of curves change with time

［1］ 崔希民，繆協興，趙英利，等. 論地表移動過程的時間函數［J］.煤炭學報，1999，24(5):453-456.

Cui Ximin，Miao Xiexing，Zhao Yingli，et al.Discussion on the time function of time dependent surface movement［J］. Journal of China Coal Society，1999，24(5):453-456.

［2］ 常占強，王金莊. 關于地表點下沉時間函數的研究——改進的克諾特時間函數［J］.巖石力學與工程學報，2003，22(9):1496-1499.

Chang Zhanqiang，Wang Jinzhuang.Study on time function of subsidence:the improved Knothe time function［J］. Chinese Journal of Rock Mechanics and Engineering，2003，22(9):1496-1499.

［3］ 徐洪鐘，李雪紅. 基于Logistic 增長模型的地表下沉時間函數［J］.巖土力學，2005(S):151-152.

Xu Hongzhong，Li Xuehong. Time function of surface subsidence based on logistic growth model［J］.Rock and Soil Mechanics，2005(S):151-152.

［4］ 王正帥，鄧喀中. 采動區地表動態沉降預測的Richards 模型［J］.巖土力學，2011，32(6):1664-1668.

Wang Zhengshuai，Deng Kazhong.Richards model of surface dynamic subsidence prediction in mining area［J］.Rock and Soil Mechanics，2011，32(6):1664-1668.

［5］ 朱廣軼，沈紅霞，王立國.地表動態移動變形預測函數研究［J］.巖石力學與工程學報，2011，30(9):1889-1895.

Zhu Guangyi，Shen Hongxia，Wang Liguo. Study of dynamic prediction function of surface movement and deformation［J］.Chinese Journal of Rock Mechanics and Engineering，2011，30(9):1889-1895.

［6］ 彭林軍，趙曉東，李術才.深部開采地表沉陷規律模擬研究［J］.巖土力學，2011，32(6):1910-1914.

Peng Linjun，Zhao Xiaodong，Li Shucai.Simulating research on rules of surface subsidence due to deep mining［J］. Rock and Soil Mechanics，2011，32(6):1910-1914.

［7］ 劉玉成，曹樹剛，劉延保.可描述地表沉陷動態過程的時間函數模型探討［J］.巖土力學，2010，31(3):925-931.

Liu Yucheng，Cao Shugang，Liu Yanbao. Discussion on some time functions for describing dynamic course of surface subsidence due to mining［J］.Rock and Soil Mechanics，2010，31(3):925-931.

［8］ 劉玉成.基于Weibull 時間序列函數的動態沉陷曲線模型［J］.巖土力學，2013，34(8):2409-2413.

Liu Yucheng. Dynamic surface subsidence curve model based on Weibull time function［J］.Rock and Soil Mechanics，2013，34(8):2409-2413.

［9］ 王世道，林福欽.兩種巖移計算方法的比較［J］.礦山測量，1986(4):22-24.

Wang Shidao，Lin Fuqin.The comparison of two calculation methods of rock movement［J］.Mine Surveying，1986(4):22-24.

［10］ 李文增，李 岐，馬 群.采動影響下覆巖破壞動態發展過程的數值模擬［J］.金屬礦山，2012(9):37-39.

Li Wenzeng，li Qi，Ma Qun. Numerical simulation of overburden rock strata fracture dynamic progressive process induced by caving［J］.Metal Mine，2012(9):37-39.

［11］ 王新豐，高明中，陳雨雪，等.基于彈性薄板理論的采場頂板破斷特征分析［J］.金屬礦山，2015(6):24-28.

Wang Xinfeng，Gao Mingzhong，Chen Yuxue，et al.Analysis of fracturing characteristics of stope roof based on elastic thin plate theory［J］.Metal Mine，2015(6):24-28.

［12］ 王啟慶，李文平，李小琴，等.采場上覆整體移動帶堅硬巖層破斷規律研究［J］.金屬礦山，2014(3):15-20.

Wang Qiqing，Li Wenping，Li Xiaoqin，et al. Study on hard strata rupture law of overlying integrated moving belt at stope［J］. Metal Mine，2014(3):15-20.

［13］ 劇成宇，鄧喀中.工作面停采后地表下沉規律研究［J］.金屬礦山，2009(4):22-25.

Ju Chengyu，Deng Kazhong.Research on the law of ground subsidence after stoping halt［J］.Metal Mine，2009(4):22-25.

［14］ 胡海峰，趙陽升，康建榮，等.煤礦采空區跨度和延續時間與地面殘余變形的相關規律及實證［J］. 巖石力學與工程學報，2008，27(1):65-71.

Hu Haifeng，Zhao Yangsheng，Kang Jianrong，et al. Related laws and verification of mined-out area span，time and residual deformation［J］. Chinese Journal of Rock Mechanics and Engineering，2008，27(1):65-71.

［15］ 王 偉，盧廷浩. 基于Weibull 曲線的軟基沉降預測模型分析［J］.巖土力學，2007，28(4):803-808.

Wang Wei，Lu Tinghao. Study on prediction model of soft foundation settlement based on Weibull curve［J］.Rock and Soil Mechanics，2007，28(4):803-808.

［16］ 任 松，姜德義，楊春和. 復雜開采沉陷分層傳遞預測模型［J］.重慶大學學報:自然科學版，2009，32(7):823-828.

Ren Song，Jiang Deyi，Yang Chunhe. Stratification transfer model for predicting complex mining subsidence ［J］. Journal of Chongqing University:Natural Science Edition，2009，32(7):823-828.

［17］ 許 冬，王臨清，吳 侃. 任意形狀工作面沉陷預計計算方法［J］.金屬礦山，2014(5):55-59.

Xu Dong，Wang Linqing，Wu Kan. Mining subsidence prediction calculation methods of random shape working face［J］.Metal Mine，2014(5):55-59.

［18］ 滕永海. 采動過程中地表移動變形計算研究［J］. 礦山測量，1997(4):17-20.

Teng Yonghai.Calculation of surface movement and deformation in mining process［J］.Mine Surveying，1997(4):17-20.

［19］ 中國統配煤礦總公司. 煤礦測量手冊［M］.北京:煤炭工業出版社，1990.

China National Coal Corporation. Coal Measure Manual［M］. Beijing:China Coal Industry Publishing House，1990.

［20］ 劉玉成.開采沉陷的動態過程模型研究［M］.長沙:中南大學出版社，2013.

Liu Yucheng. Study of the Ground Surface Dynamic Subsidence Model Due to Underground Coal Mining［M］. Changsha:Central South University Press，2013.

［21］ 劉玉成.煤層開采地表移動過程的FLAC3D模擬研究［J］.煤炭科學技術，2012，40(5):93-95.

Liu Yucheng.Study on FLAC3Dsimulation of surface ground movement process for underground seam mining［J］. Coal Science and Technology，2012，40(5):93-95.