Meissel－Stokes核函數應用于區域大地水準面分析

榮 敏，周 巍，任紅飛

（1．信息工程大學 地理空間信息學院，河南 鄭州450052；2．西安測繪研究所，陜西 西安710054；3．西安測繪總站，陜西 西安710054）

精化大地水準面是滿足大地測量和諸多地球科學發展需要的一項重要工作。Stokes理論框架下建立邊值問題計算大地水準面時，理論上需要在全球范圍內進行求解［1－2］。但由于測量數據、成本以及計算效率等多個方面的原因，實現全球積分不太可能［3－4］。為了解決此問題，提高計算精度，有關學者提出多種改善方式，通常是將積分域分為球冠（近區）和剩余部分（遠區）［3－4］，近區應用Stokes公式積分計算，忽略其遠區影響。再者是基于高精度地球重力場模型，采用移去－恢復法，移去重力場中的低頻（長波）影響［5］。在此基礎上，還可考慮采用修正St okes核函數，改善標準Stokes特性，提高近區計算能力，減弱其遠區效應等。

較早的修正Stokes核函數理論有：M．S．Molodensky（1962）、Wong和Gore（1969），以及Meissl（1971）等［6－15］。2003年，Michael Kern對于多種修正Stokes核函數，基于EGM96和GPM98B進行研究分析，認為Meissel－Stokes具有計算速度快、實現方便、遠區影響小等特點［11］。2013年，傅露等結合DNSC08－CRA模型中的美國重力數據，分析比較幾種修正Stokes核函數，得出采用修正Stokes核函數 可有效改善計算精度 其中Meissel－Stokes核函數，計算簡單，速度較快，是一種較優的修正Stokes核函數［12］。2007年，李建成提出在厘米級精度要求下，重新研究Stokes核函數和構造截斷函數問題［3－4］。研究修正Stokes核函數，是實現建立厘米級精度大地水準面的主要理論問題和關鍵技術之一。文獻［16］中認為使用標準Stokes核函數會遺漏部分長波影響，而引入誤差。因此，本文基于EGM2008地球重力場位系數模型，分析討論Meissel－Stokes和標準Stokes核函數特性，并利用它們計算大地水準面差距，比較兩者計算大地水準面精度，用以精化區域大地水準面。

1 大地水準面計算

應用Stokes公式計算大地水準面差距N的表達式為［1－2］

式中：R為地球平均半徑；γ0為正常重力異常；Δg（R，Ω′）為大地水準面上的重力異常值；Ω′為積分面；dΩ′＝sin?′d?′dλ′＝sinψdψdα；?′和λ′為積分點余緯和經度；ψ為計算點與積分點之間的角距；α為計算點至積分點方向的方位角。

標準Stokes核函數為［15］

通常將積分區域劃分為近區和遠區，即Ω0為近區，Ω－Ω0為遠區，則式（1）可重新表達為

采用移去－恢復法，移去地球重力場模型，計算至n＝L階時的重力異常值ΔgL，獲取剩余重力異常值Δgres，計算剩余大地水準面差距Nres，其算式為

利用地球重力場位系數模型，模型重力異常Δgn的算式為式中：GM為地心引力常數；Cnm和Snm為完全正常化的球諧系數；ˉPnm（cos?）是完全規格化締合Legendre函數；?和λ分別為地心緯度和經度；n和m分別為地球重力場模型的階與次。

近區，當ψ＝0°時，Stokes積分式存在弱奇異。求解該問題時，需要做一小變化，用以減弱奇異計算，則近區大地水準面差距的計算公式，可表示為

Q0為零階截斷誤差系數，則有

遠區效應，一般考慮使用地球重力場位系數模型計算，算式為

式中：ψ0為截斷積分半徑；εn為重力場位系數誤差；Qn（ψ0）為截斷誤差系數，其算式為

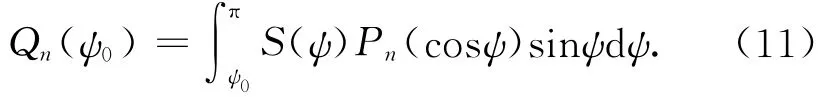
式中：Pn（cosψ）為Legendre多項式。

遠區效應的計算誤差主要由地球重力場位系數誤差和截斷誤差組成。重力場模型位系數誤差是隨著重力場模型生成而存在，屬于已知量。截斷誤差是指模型階次截斷至L階所引起的誤差，是遠區效應的主要影響量。截斷誤差小，遠區效應就小，則在一定精度下可忽略其影響。

2 Meissel-Stoke核函數S M（ψ）應用于大地水準面計算

1966年，De Witte發現在原Stokes核函數零交點處的截斷誤差比較小。基于該理論，1971年Meissel給出了Meissel－Stokes公式［9－15］，則有

近區，將式（12）代入式（6），替換原標準Stokes核函數，則有

遠區效應δNM的計算表達式為［9－15］

式中：Qmn（ψ0）為Meissel－Stokes核函數相應的截斷誤差系數。

Meissel－Stokes截斷誤差系數計算式中，應用Legendre多項式循環迭代關系，其截斷誤差收斂速度較快，尤其在采用移去－恢復法時效果明顯。

3 精度檢測

利用EGM2008重力場位系數模型和實驗區內的重力點數據，評價Meissel－Stokes核函數應用于區域大地水準面差距計算。首先，計算重力點移去L＝120階，計算至360階的重力異常模型值，作為殘余重力異常值Δg121－360然后 基于重力點的殘余重力異常值，生成2．5′×2．5′格網值；接著，采用Stokes公式，計算殘余大地水準面差距Nres，經恢復，獲得大地水準面差距N′360；最后，以EGM2008位系數模型，n＝2～360獲得的NM360為真值，求差值δN，統計其精度，具體的計算過程見式（17）、式（18）。

差值δN當中包含遠區效應的截斷誤差、重力場模型位系數引入的誤差，以及重力數據格網化和積分離散化誤差。

4 計算與分析

為評價Meissel－Stokes核函數在區域大地水準面精化中的應用，首先，分析核函數和截斷誤差系數與積分半徑及模型階次關系；然后，計算分析兩重力點截斷誤差隨積分半徑的變化。

4．1 核函數和截斷誤差系數分析

基于EGM2008地球重力場位系數模型，分析標準Stokes核函數和Meissel－Stokes核函數與截斷積分半徑關系，如圖1所示。分別取截斷積分半徑為1°，3°，6°和12°，其截斷誤差系數，隨重力場位系數模型階次變化情況，如圖2所示。

圖1 核函數隨0°≤ψ≤6°的變化

由圖1可見，Meissel－Stokes函數和標準Stokes核函數，都隨著球面角距的增加，其值逐漸減小；當球面角距在0．5°范圍以內，核函數值變化較為劇烈；當球面角距大于0．5°時，其相對平緩。Meissel－Stokes函數收斂速度快于標準Stokes核函數。截斷積分半徑越小，Meissel－Stokes函數值變化越大，與Stokes核函數的差異也相對較大。

由圖2可見，Meisel－Stokes截斷誤差系數，截斷積分半徑為1°時，其截斷階次在120階收斂至0附近；截斷積分半徑為3°和6°時，其截斷階次大致在70階，收斂至0附近。當截斷積分半徑為12°時，在大約20多階，收斂至0附近。

整體上，模型截斷階次越高，則截斷誤差系數值越小，并隨之逐漸穩定。截斷積分半徑越大，收斂速度越快。當截斷階次L≥120階時，Meissel－Stokes的截斷誤差系數值都在0附近。而標準Stokes核函數計算值，相對變化劇烈，其大都取至L≥180時，相對穩定。

圖2 截斷誤差系數隨模型階次的變化

4．2 截斷誤差分析

在實驗區，選取兩個重力點，具體情況見表1。利用EGM2008重力場位系數模型，分析標準Stokes和Meissel－Stokes核函數，截斷至L＝120時，分別取截斷積分半徑為1°，3°和6°，截斷誤差隨著模型階次的變化見圖3所示。

由圖3可見，隨著截斷半徑增加，截斷誤差值減小。基于Meissel－Stokes核函數的截斷誤差，相對標準Stoke核函數的計算值，要穩定且量值要小。標準Stokes核函數計算的截斷誤差，在后相對穩定。地形高也對截斷誤差略有影響。由此可見，采用Meissel－Stokes核函數，解算至120階，其截斷誤差影響趨于穩定。

表1 截斷誤差計算點

圖3 截斷誤差圖（m）

4．3 Meissel-Stokes核函數應用分析

實驗區位于北緯28°～32°，東經108°～114°，東部較為平坦，西部為多山區。其中分布有8 564個實測重力點值，高程最大值為2 890．5 m，最小值為18．2 m，平均值為233．4 m。實際地形見圖4。

圖4 實驗區地形圖

為評價Meissel－Stokes核函數，利用EGM2008地球重力場位系數模型，截斷至L＝120階，計算實驗區內，大地水準面上的殘余重力異常模型值，并生成2．5′×2．5′格網值，統計值見表2。

表2 基于EGM2008模型的實驗數據統計表 mGal

選用積分半徑為1°，截斷階次為L＝120，計算殘余大地水準面差距，統計結果見表3。恢復后，獲得的大地水準面差距結果，統計情況見表4；圖5（a）為L＝360階，EGM2008模型計算的大地水準面差距；圖5（b）為由標準Stokes核函數，計算獲得大地水準面差距；圖5（c）為由Meissel－stokes核函數，計算的大地水準面差距。統計大地水準面差距的偏差，結果見表5。

圖5 大地水準面差距圖（m）

由圖5可見，基于標準Stokes和Meissel－Stokes核函數計算的大地水準面差距都與模型值趨勢接近；但相對而言，標準Stokes核函數計算的大地水準面差距與模型值的差異明顯。

表3 剩余大地水準面差距計算值統計 m

表4 大地水準面差距計算值統計 m

表5 大地水準面差距計算值與模型值的偏差統計表m

由表3～表5可知，基于標準Stokes核函數，移去L＝120，計算大地水準面差距值，比EGM2008模型值小；最大相差大約0．8 m；平均值相差0．02 m以內。基于Meissel－Stokes核函數，計算的大地水準面差距，較模型值偏大；最大相差在大約0．2 m；平均值相差大約0．01 m。基于Meissel－Stokes核函數，采用1°積分半徑，較標準St okes核函數計算的大地水準面差距，標準偏差小。

由表5可知，利用Stokes和Meissel－Stokes核函數計算的大地水準面差距，與模型值存在偏差。究其原因一是截斷積分半徑和截斷階次有限性；二是截斷誤差較大；三是地球重力場位系數誤差；四是重力點數據分布不均勻，格網化時引入了誤差；五是Stokes積分離散化誤差引入的誤差等。但相對而言，Meissel－Stokes計算精度比Stokes計算精度要好。

5 結束語

基于EGM2008重力場位系數模型，精化區域大地水準面計算時，認為截斷至120階以上，積分半徑≥6°時，可忽略其遠區效應。而實際上，由于測量數據有限性，很難達到所需的積分半徑要求，因此可考慮選用Meissel－Stokes核函數，它收斂速度快，截斷誤差小且穩定。相同條件下，采用Meissel－Stokes計算大地水準面差距，其精度比標準Stokes核函數計算大地水準面的精度高。由此可見，在大地水準面精化工作中，采用移去－恢復法，應用Meissel－Stokes核函數，可提高大地水準面的計算精度，為實現建立厘米級精度大地水準面這一目標服務。

［1］ 陸仲連．地球重力場理論與方法［M］．北京：解放軍出版社1996年．

［2］ HOFMANN－WELLENHOF B，MORITZ H．Physical geodesy［M］．second edition，Springer Wien New Yor k，2006．

［3］ 李建成．我國現代高程測定關鍵技術若干問題的研究及進展［J］．武漢大學學報：信息科學版，2007，32（11）：980－987．

［4］ 李建成．最新中國陸地數字高程基準模型：重力似大地水準面CNGG2011［J］．測繪學報，2012，41（5）：651－660，669．

［5］ 劉曉剛，劉雁雨，曹紀東，等．GPS水準采用移去－恢復技術擬合大地水準面方法的研究［J］．測繪工程，2008，17（3）：70－73．

［6］ 魏子卿，王剛．用地球位模型和GPS／水準數據確定我國大陸似大地水準面［J］．測繪學報，2003，32（1）：1－5．

［7］ 傅露，褚永海．區域大地水準面確定中Stokes核函數的應用［J］．大地測量與地球動力學，2013，33（2）：110－113，119．

［8］ FEATHERSTONE W E，EVANS J D，OLLIVER J G．A Meissl－modified Vanicek and Kleusberg kernel to reduce the truncation error in gravi metric geoid computations［J］．Journal of Geodesy，1998，72：154－160．

［9］ SJ?BERG L E，HUNEGNA W A．Some modifications of Stokes for mula the account for truncation and potential coefficient errors［J］．Journal of Geodesy，2000，74：232－238．

［10］SJ?BERG L E．A computational scheme to model the geoid by the modified Stokes f or mula without gravity reductions［J］．Journal of Geodesy，2003，77：423－432．

［11］ELL MANN A．Two deter ministic and three stochastic modifications of Stokes’s f or mula：a case study f or the Baltic countries［J］．Journal of Geodesy，2005，79：11－23．

［12］VANICEK P，FEAT HERSTONE W E．Perfor mamce of three types of Stokes’s ker nel in the combined solution f or the geoid［J］．Journal of Geodesy，1998，72：684－697．

［13］EVANS J D，FEATHERSTONE W E．Improved convergence rates f or the tr uncation error in gravimetric geoid deter mination［J］．Journal of Geodesy，2000，74：239－248．

［14］KERN M．An Analysis of the Combination and Downward Continuation of Satellite，Airborne and Terrestrial Gravity Data［R］．Canada：University of CALGARY，2003．

［15］SPRLAK M．Generalized geoidal estimators f or deterministic modifications of spherical Stokes’f unction［J］．Contributions to Geophysics and Geodesy，2010，40（1）：45－64．

［16］WANG Y M，SALEH J，LI X，et al．The US Gravimetric Geoid of 2009（USGG2009）：model develop ment and evaluation［J］．Journal of Geodesy，2012，86：165－180．