湍流大氣中動態激光散斑的數值模擬

韓星星

(西安交通大學城市學院，陜西 西安710018)

1 引言

利用目標激光散斑特征對目標的運動特征進行檢測在軍事和民用領域具有重要的應用價值。自20世紀80年代以來，國內外大批學者對漫射平面、圓柱、圓錐、球等多種目標平動、轉動以及振動狀態下的散斑特性進行了大量的理論和實驗研究［1－2］。隨著計算機技術的發展，數值模擬逐漸成為一種重要的研究手段，2004年李小兵等人提出了利用激光散斑實時測量目標散射面角振動的原理，并從干涉條紋的角度對仿真參數進行了分析，模擬了兩個散射元的情況［3］。但是這種模擬方法由于效率太低而無法用于大量散射元情況。1999年程傳福等人對高斯隨機表面光散射產生的散斑場進行了模擬并分析了散斑光強的概率密度函數［4］，但是該算法只適用于夫瑯和費區。

在實際應用中，激光的發射和接收通常都是在大氣環境下進行的，受到大氣湍流的影響，激光會發生閃爍、漂移、展寬等現象。這些現象對目標回波散斑特征產生不可忽視的影響。經過幾十年的研究，人們已經發展出了幾何光學、Rytov近似、Markov近似等解析方法來計算激光的傳輸特性，但它們都是在一定條件下的近似，其適用范圍有限。而數值方法由于其廣泛的適應性得到眾多研究者的重視，其中研究最多的是分步傅里葉方法。

分步傅里葉方法是求解拋物方程的一種通用的方法，在多個領域都有應用。從20世紀80年代開始，國內外學者就不斷地把分步傅里葉方法應用到光波在大氣中的傳輸計算中［5－8］，但多數文獻模擬的都是靜止光斑，無法體現光斑隨時間的變化特性。本文首先在無湍流的情況下利用分步傅里葉算法，模擬了真空中的動態散斑場，然后結合凍結場理論，模擬了湍流大氣中的動態散斑場，并分析了兩種情況下激光回波散斑場的時空相關特性。

2 分步傅利葉算法的推導

在圖1所示的系統中，激光器發射孔徑位于平面z=0上，光軸與z軸平行，接收器位于平面z=L，s和ρ分別是發射平面和接收平面上垂直于傳播軸的位置矢量。在發射平面上，單位振幅高斯波束的光場為:

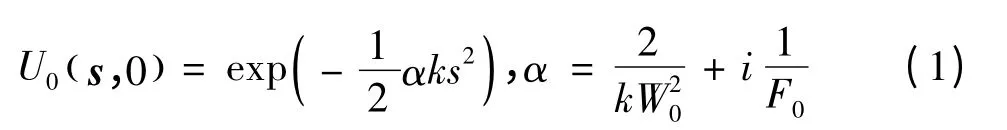
其中，k是波數;W0是波束有效半徑;F0是波前曲率半徑。

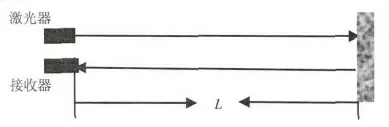
圖1 激光散斑測量示意圖

分步傅里葉算法是一種在電磁波及光波傳輸模擬領域廣泛應用的方法，算法原理公式［9］為:

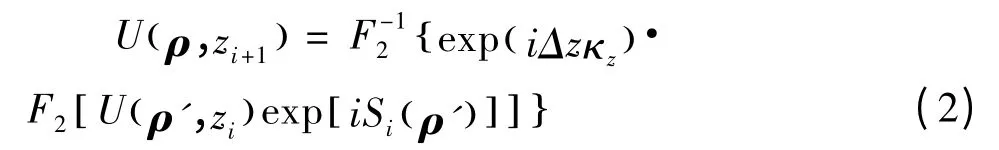
為了利用數值方法計算式，其中的U和S都要經過離散化［10－11］:

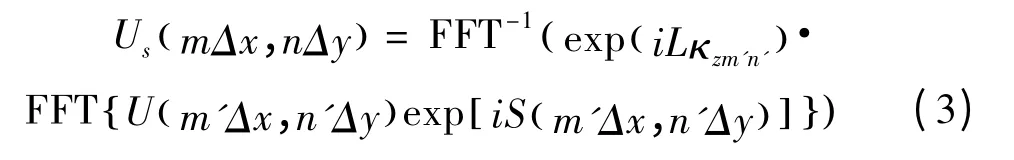
把相位屏劃分為N×N的正方形網格，場和相位屏只在網格結點上有值。當激光在真空中傳播并被漫射面反射時，其模擬過程只需要一個相位屏，這個相位屏代表了漫反射面，其生成方法為:

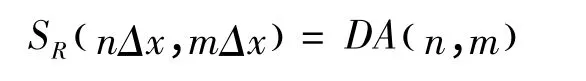
其中，D是相位屏的均方差;A是獨立均勻分布的隨機數矩陣。

為了考察散斑的動態特征，需要模擬當物體運動時，不同時刻的散斑圖樣。式(3)可變形為:

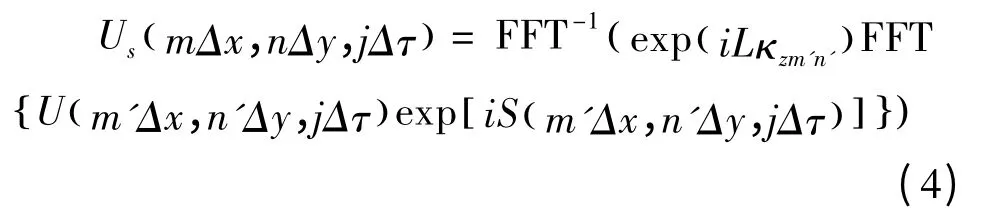
假設目標以速度v沿x軸正向平動，則相位屏也要做相同的運動，即:

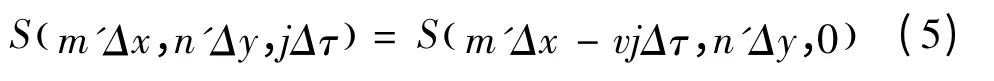
如果l=vnΔτ/Δx是整數，則在模擬第j個散斑時，直接把矩陣S沿x軸正向移動l個網格，空出來的網格點用新生成的隨機數補上即可。但是在一般情況下，l不是整數，而漫射面的性質決定了不能用插值方法得到任意位置的S。本文采用沿相反方向移動光源的方法，對于第n個散斑，發射波束為:

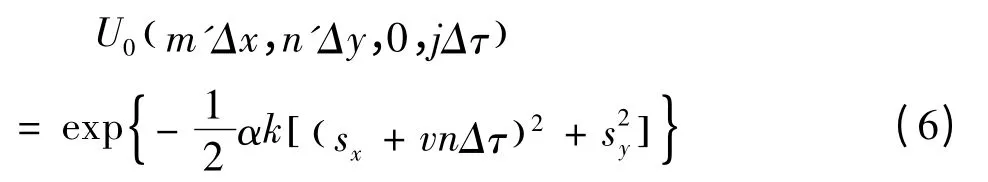
3 真空中散斑的模擬

選擇發射波為準直的高斯波束，波長λ=1．06μm，初始半徑W0=3 cm，半徑為WR=3 cm的漫射圓盤距離波源L=2000 m，目標以v=2 m/s的速度沿x方向移動，單站接收。不考慮大氣湍流對激光的擾動，圖2給出了不同時刻接收面上的散斑圖樣。

可以看到相鄰時刻的兩幅圖都有較強的相似性，時間間隔越大，散斑圖樣相差也越大。隨著時間的推移，亮斑的位置發生的移動，且形狀發生了變化，有的亮斑消失了，并有新的亮斑生成，即通過模擬圖像觀察到了動態散斑現象中的平移和沸騰現象。

利用模擬得到的散斑可以統計計算散斑場的空間相關函數，它反映了散斑場隨著橫向位置移動的變化快慢，決定了散斑顆粒的尺寸。圖3給出了當初始半徑不同時，散斑場空間相關函數隨著兩點距離的變化，它們對獨立生成的100個散斑圖樣進行統計得到的。三條曲線中，當W0=3 cm時激光的散斑場空間相關函數下降最慢，其次是W0=5 cm和W0=1 cm。在真空中當初始半徑分別為W0=1，3，5 cm時，照射在目標平面上的光斑半徑分別為W=3．8，4．2，5．4 cm，這說明散斑尺寸是由目標平面上的光斑半徑決定的，這和理論公式是一致的，即光斑半徑越小，散斑尺寸越大。

圖2 真空中漫射面回波動態散斑圖樣

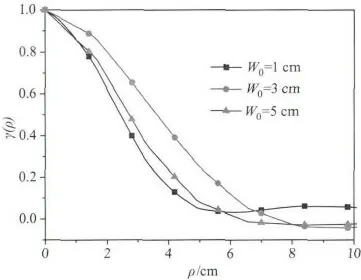
圖3 真空中漫射面回波散斑場空間相關函數

利用一系列不同時刻的散斑圖樣可以統計計算散斑圖樣相關程度隨著時間間隔的變化。圖4顯示了不同初始半徑的激光散斑圖樣時間相關函數。可以看出時間相關函數的下降速度與目標移動速度成正比。對于不同的初始半徑的激光，散斑時間相關函數的下降速度由快到慢依次是W0=1，5，3 cm，這和空間相關函數的變化是不同的。這說明，時間相關函數不但和目標平面上的光斑半徑有關，還和目標平面上的光斑相位分布有關。當W0=3 cm時的光斑最小，其散斑最大，相應的相關時間最大。W0=1 cm時的光斑雖然小于W0=5 cm，但是當W0=1 cm時，光斑上的相位變化要更劇烈，從而造成目標移動時，散斑相關時間的減小，所以W0=1 cm時的相關時間最小。

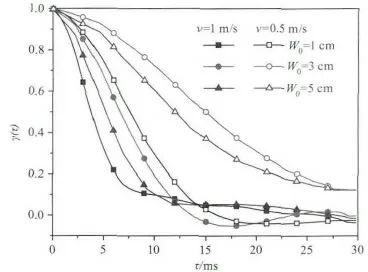
圖4 真空中漫射面回波散斑場時間相關函數

4 湍流中的散斑模擬

當傳輸路徑處于湍流之中時，激光在前向傳輸和反射過程中受湍流的擾動，振幅和相位都會發生變化，形成的散斑場的統計特性也會發生變化。湍流對光場的擾動也可以利用相位屏模擬，但是只有當路徑較短，湍流擾動較小時，才可以把整個路徑的湍流等效為一個相位屏，對于較長的路徑及較強的湍流(σ2I=1．23C2nk7/6L11/6＞0．1)時，把整個路徑劃分為多段，每個段路徑上的湍流都可以等效為一個隨機相位屏，第(i+1)個相位屏上的場可以利用式(4)由第i個相位屏上的場得到，以此類推即可由發射場得到散射場。

湍流是由空氣運動形成的，所以湍流通常還伴隨著一定速度的風，根據凍結場理論，對散斑場時間統計特性有影響的是風的橫向速度。假設風的速度矢量為vw=vxex+vyey，其中ex、ey分別是沿x、y方向的單位矢量。在Δτ的時間間隔內，湍流等效相位屏沿x、y方向移動的網格數分別為lx=vxnΔτ/Δx和ly=vynΔτ/Δx。由于湍流折射率譜的能量主要集中在低頻，所以其等效相位屏起伏在空間上較為緩慢，當lx和ly不是整數時，平移后的相位屏可以采用插值的方法得到。

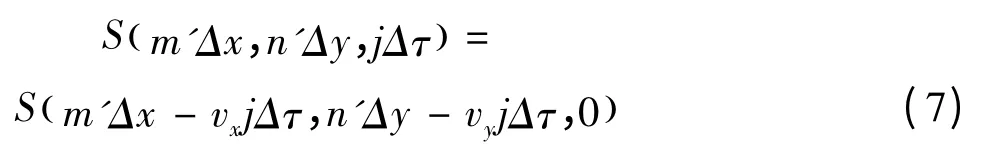
其中，S( m'Δx－vxjΔτ，n'Δy－vyjΔτ，0)可以利用三次樣條插值方法由S( m'Δx，n'Δy，0)得到。

當目標運動時，本文采用反向移動整個系統的方法，此時湍流等效相位屏的移動速度應采用v'w= ( vx－v) ex+vyey。在相位屏移動時，必須保證進入有效計算范圍內的部分相位屏不能成為空白，所以模擬過程中生成長和寬都為2N的相位屏，當vx－v和vy都為正時，漫射目標的等效相位屏與湍流等效相位屏第一象限重疊，這樣可以最大限度的利用生成的相位屏。當v'w為其他值時，依此類推。

在上一節激光散射系統的基礎上考慮大氣湍流效應，湍流結構常數為C2n=1．8×10－14m－2/3，單程路徑上的Rytov方差為σ2I=2，單程路徑被平均分為20段，整個路徑共設置了40個湍流等效相位屏和一個目標等效相位屏。不考慮前、后向路徑上湍流的相關性，即前、后向路徑上的相位屏均不相同。

圖5給出了湍流大氣中不同時刻接收面上的散斑圖樣，其中目標運動速度為vt=1．0exm/s，風速度矢量vw=－1．0exm/s。相比真空中的散斑，湍流中的散斑樣本的不同之處有三點，一是散斑平均尺寸變小了;二是真空中的散斑邊緣比較光滑，而湍流中的散斑邊緣更加不規則;三是湍流中的散斑隨著時間的變化更快，第四幅散斑圖和第一幅已經觀察不到相似性。

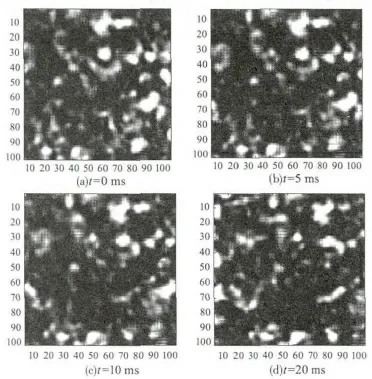
圖5 湍流中漫射面回波動態散斑圖樣

圖6 顯示了不同初始半徑的高斯波束在湍流中照射到無窮大漫射平面形成的散斑場的空間相關函數，它們對獨立生成的100個散斑圖樣進行統計得到的。與圖3相比可以發現，在湍流中空間相關函數下降速度更快，這代表著散斑尺寸更小，這與圖5顯示的信息是一致的。三條曲線下降速度的排序與圖3中相同，這表明了湍流對不同初始半徑的激光散斑影響大致是相同的。

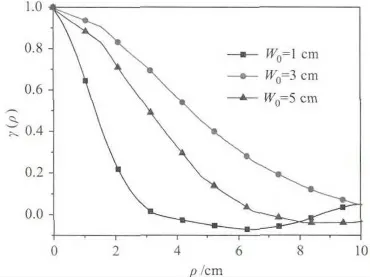
圖6 湍流中漫射面回波散斑場空間相關函數

圖7 顯示了湍流大氣中不同初始半徑的激光散斑圖樣時間相關函數。在湍流大氣中，即使目標不運動，受湍流效應的影響散斑場仍然隨時間變化。當目標運動和風的運動同時存在時，散斑受雙重作用調制，時間相關函數下降速度更快，即相關時間變得更小。而風速沿不同方向時，時間相關函數變化不大，說明湍流和目標對散斑場的影響是相互獨立的。

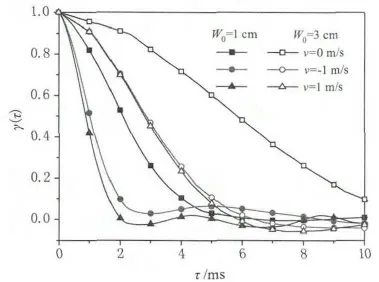
圖7 湍流中漫射面回波散斑場空間相關函數

5 討論與結論

本文采用分步傅里葉算法模擬了真空和湍流大氣中激光照射漫射面后，反射波形成的散斑場。并在該方法中引入了時變相位屏，從而模擬了當漫射面運動時以及湍流隨著風向運動時，散斑場隨著時間的變化。對模擬得到的散斑進統計計算，得到了散斑場的空間和時間相關函數。結果表明，相關長度由目標上的光斑尺寸決定，光斑越大，接收面上的散斑越小。而相關時間不僅受目標平面上的光斑尺寸影響，還受目標平面上的光場相位影響，光場相位隨著位置的變化越快，相關時間就越短。本文研究結果為在湍流大氣中利用散斑遠程測量目標運動速度提供了理論基礎。

［1］ A Hayashi，Y Kitagawa．High－resolution rotation－angle measurement of a cylinder using speckle displacement detection［J］．Appl．Opt．1983，22(8):3520－3525．

［2］ QIN Yuwen，DAI Jiabin，CHEN Jinlong．Developments on electronic speckle method［J］．Journal of Experimental Mechanics，1996，11(7):410－416．(in Chinese)秦玉文，戴嘉彬，陳金龍．電子散斑方法的進展［J］．實驗力學，1996，11(7):410－416．

［3］ LI Xiaobing，PENG Renjun，WU Jian．Real－time measurement of the object angular vibration by laser speckles［J］．High Power Laser and Particle Beams，2004，16(4):413－416．(in Chinese)李小兵，彭仁軍，吳健．目標角振動的散斑法實時測量［J］．強激光與粒子束，2004，16(4):413－416．

［4］ CHENG Chuanfu，QI Dongping，LIU Deli，et al．The computational simulations of the Gaussian correlation random surface and its light－scattering speckle field and the analysis of the intensity probability density［J］．Acta Physica Sinica，1999，48(9):1635－1643．(in Chinese)程傳福，亓東平，劉德麗，等．高斯相關隨機表面及其光散射散斑場的模擬產生和光強概率分析［J］．物理學報，1999，48(9):1635－1643．

［5］ M Z M Jenu，D H Bebbington．Fourth－moment calculation of optical propagation in a turbulent atmosphere with use of the split－step method．I．Plane wave［J］．J．Opt．Soc．Am．A．，1994，11(11):2862－2870．

［6］ J M Martin，S M Flatte．Intensity images and statistics from numerical simulation of wave propagation in 3－D random media［J］．Applied Optics，1998，27(11):2111－2126．

［7］ RAO Ruizhong．Pattern characteristics of collimated laser beam in a turbulent atmosphere I．Characteristic Radii［J］．Chinese Journal of Lasers，2002，29(10):879－894．(in Chinese)饒瑞中．湍流大氣中準直激光束的光斑特征Ⅰ．特征半徑［J］．中國激光，2002，29(10):879－894．

［9］ QIAN Xianmei，RAO Ruizhong．Spatial distribution of Gaussian－beam scintillation in atmosphere by numerical simulation［J］．Chinese Journal of Quantum Electronics，2006，23(3):320－324．(in Chinese)錢仙妹，饒瑞中．高斯光束大氣閃爍空間分布的數值模擬研究［J］．量子電子學報，2006，23(3):320－324．

［10］WANG Lijin，LI Qiang，WEI Honggang，et al．Numerical simulation and validation of phase screen distorted by atmospheric turbulence［J］．Opto－Electronic Engineering，2007，34(3):1－5．(in Chinese)王立瑾，李強，魏宏剛，等．大氣湍流隨機相位屏的數值模擬和驗證［J］．光學工程，2007，34(3):1－5．

［11］ZHANG Huimin，LI Xinyang．Numerical simulation of wavefront phase sceen distorted by atmospheric turbulence［J］．Opto－Electronic Engineering，2006，33(1):14－19．(in Chinese)張慧敏，李新陽．大氣湍流畸變相位屏的數值模擬方法研究［J］．光電工程，2006，33(1):14－19．