位移譜阻尼調整系數模型研究

王國弢等

摘要：基于408條地震地面運動記錄的統計分析，首先研究了地震動持時、矩震級、斷層距和場地類別等對阻尼調整系數的影響，然后采用非線性回歸分析提出了能體現持時和矩震級影響的阻尼調整系數模型.研究結果表明：持時和矩震級對阻尼調整系數有顯著的影響，而斷層距和場地類別影響較弱；阻尼調整系數相對于阻尼比存在異方差性；持時的影響可以通過在模型中包含線性震級項來體現.本文所提出的包含線性矩震級項的阻尼調整系數模型既能體現矩震級的影響，也能間接地體現地震動持時對阻尼調整系數的影響；模型的標準差能體現阻尼調整系數相對于阻尼比的異方差性.本文的研究結果可直接用于阻尼比為5%的位移譜衰減模型，也可為我國抗震設計規范的制訂和修改提供參考.

關鍵詞：地震動持時；矩震級；斷層距；場地類別；阻尼調整系數；阻尼；位移譜衰減模型

中圖分類號：P315；TU352.1 文獻標識碼：A

位移反應譜衰減模型在地震危險性分析和工程結構的抗震設計及分析中具有十分重要的意義.通常的統計分析僅給出阻尼比為5%的位移反應譜衰減模型，而實際結構具有各種阻尼比，對每一阻尼比都提供一個衰減模型是不切實際的，因而需要采用阻尼調整系數將阻尼比為5%的位移反應譜衰減模型調整到其它阻尼比的位移反應譜衰減模型.在阻尼比為5%的位移反應譜衰減模型的基礎上，通過阻尼調整系數得到其它阻尼比位移反應譜衰減模型的合理性及可靠性取決于阻尼調整系數的合理性及可靠性.在這方面，國外已有不少學者對其進行了研究：如Newmark和Hall1，Wu和Hanson2及Idriss3提出了考慮阻尼比和周期影響的位移譜阻尼調整系數回歸方程，Ashour4及Tolis和Faccioli5提出了僅考慮阻尼比影響的位移譜阻尼調整系數回歸方程；而國內學者主要針對我國抗震規范6-7中設計反應譜阻尼調整系數的不足，建議了相應的改善方法或對其適用性進行了評價，如胡聿賢8及王曙光等9提出了與周期和阻尼比有關的阻尼調整系數，曹加良等10對我國抗震規范設計反應譜阻尼調整系數進行了定性的評價.以上研究僅考慮了結構自身參數主要是自振周期和阻尼對阻尼調整系數的影響，并沒有考慮結構外部因素如震級、斷層距、場地條件、地震動持時等對阻尼調整系數的影響.近年來，不少學者開始對外部因素的影響進行研究，如Lin和Chang11研究了場地條件對位移譜阻尼調整系數的影響，對不同場地類別給出了相應的阻尼調整系數回歸方程，結果表明，場地類別對阻尼調整系數的影響較弱；Bommer和Mendis12及Cameron和Green13初步探討了矩震級、斷層距、場地條件和地震動持時等對位移譜阻尼調整系數的影響，但并未進行深入定量的分析；Stafford 等14則在Bommer和Mendis研究的基礎上，定量地分析了地震動持時對位移譜阻尼調整系數的影響，并提出直接考慮地震動持時的阻尼調整系數模型，但由于目前所使用的位移譜衰減模型15-19均未包含持時這個參數，所以直接包含地震動持時的阻尼調整系數模型不便于工程應用.鑒于以往研究的不足，本文首先深入地研究了各種外部因素對位移譜阻尼調整系數的影響.研究表明：持時和矩震級對阻尼調整系數有顯著的影響；斷層距和場地類別影響較弱可忽略.然后根據地震動持時與矩震級存在正的強相關性20，且譜衰減模型15-19中均包含了矩震級這個參數，本文采用非線性回歸分析提出了僅包含矩震級項的位移譜阻尼調整系數模型.最后通過模型的殘差分析，驗證了提出的模型能間接地考慮地震動持時對位移譜阻尼調整系數的影響.

1地面運動加速度時程記錄

本文使用了408條地震地面運動記錄，這些地面運動記錄下載于太平洋地震工程研究中心的強震數據庫http： peer.berkeley.edupeer ground motion database.地面運動記錄的相對能量持時21D5-95分布在1.4～80.3 s之間，矩震級Mw分布在5～8之間，觀測點到斷層破裂面的最近距離Rrup分布在0.1～100 km之間，地表厚度30 m內平均剪切波速Vs，30分布在116.3～2 016.1 ms之間，峰值地面加速度PGA分布在0.1～1.434 5 g之間.

2阻尼調整系數的概率分布

位移譜阻尼調整系數被定義為：

DSFξ，T=SDξ，TSD5%，T. 1

式中：DSF為位移譜阻尼調整系數；ξ為阻尼比；T為單自由度體系的自振周期；SDξ，T為ξ≠5%，周期為T時彈性單自由度體系的位移譜值；SD5%，T為ξ=5%，周期為T時彈性單自由度體系的位移譜值.通常可以認為在指定周期和阻尼比處的位移譜值服從對數正態分布22，對式1兩邊取自然對數有：

ln DSFξ，T=ln SDξ，T-ln SD5%，T.

2

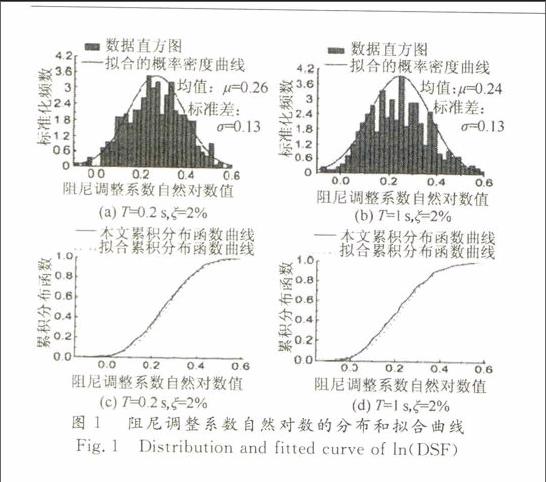
由式2可知，如果SDξ，T與SD5%，T不相關，則lnDSFξ，T服從正態分布，DSF服從對數正態分布.但是SDξ，T與SD5%，T是相關的，所以在理論上DSF并不嚴格服從對數正態分布.根據本文的分析，在T∈0.1， 7.5的范圍內，lnDSFξ，T與正態分布曲線擬合得較好；而在此周期范圍外，擬合結果并不理想，如圖1所示.圖 1給出了ξ=2%時，在T=0.2 s和1 s處，lnDSF數據點的直方圖、累積分布函數曲線圖及相應的正態分布函數的擬合結果.

在指定的周期和阻尼比處，本文認為阻尼調整系數近似地服從對數正態分布，并取回歸模型為：

lnDSF=μξ，T，X+ε. 3

式中：μξ，T，X為lnDSF的期望；X為對阻尼調整系數有顯著影響的外部因素向量；ε為隨機誤差且ε～N0，σ2；σ2為方差.由于阻尼調整系數近似服從對數正態分布，以下的統計分析中均采用阻尼調整系數的中值.

3外部因素對阻尼調整系數的影響分析

本文采用軟件SeismoSignal對每條輸入地震波分別計算了11個阻尼比下的位移譜，這11個阻尼比分別為：0.5%，1%，2%，3%，5%，7%，10%，15%，20%，25%和30%.對每個阻尼比，單自由度體系取如下20個周期：0.02，0.04，0.06，0.08，0.10，0.14，0.20，0.24，0.30，0.40，0.50，0.60，0.80，1.00，2.00，3.00，4.00，5.00，7.50和10.00 s.然后再根據式1，對每條輸入地震波求得各阻尼比下的位移譜阻尼調整系數.

3.1地震動持時的影響

工程中對于地震動持時有各種不同的定義，本文采用的持時為相對能量持時21D5-95，即從地震動能量達到總能量的5%開始至達到總能量的95%為止所經歷的時間.總能量定義為地面加速度平方的積分，即Arias強度23.

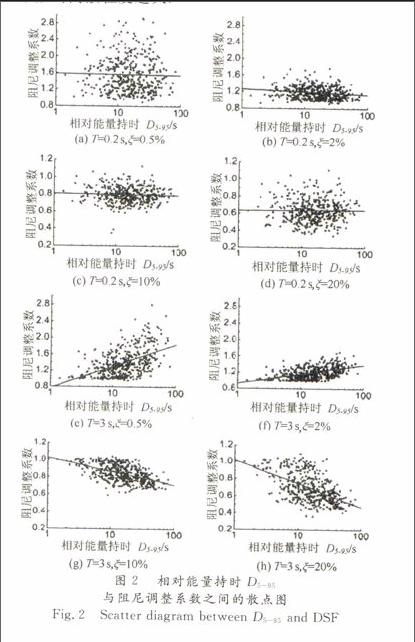
為了研究D5-95對阻尼調整系數的影響，本文作出了不同周期和阻尼比處的阻尼調整系數與D5-95之間的散點圖.限于篇幅，圖2僅給出了周期T=0.2 s和3 s時，分別在阻尼比ξ=0.5%，2%，10%和20%處，阻尼調整系數與D5-95之間的散點圖.圖2中直線為阻尼調整系數和D5-95的線性擬合線，其斜率表明了D5-95對阻尼調整系數的影響程度.由圖2可知，D5-95對阻尼調整系數的影響與周期和阻尼比有關：在短周期范圍內如T=0.2 s，見圖2a～d，D5-95對阻尼調整系數無顯著影響，而在短周期范圍外如T=3 s，見圖2e～h，當ξ<5%時，阻尼調整系數隨D5-95的增加而增加，且阻尼比越小這種趨勢越明顯；當ξ>5%時，阻尼調整系數隨D5-95的增加而減小，且阻尼比越大這種趨勢越明顯.圖2還表明了阻尼調整系數相對于阻尼比存在異方差性，即隨著阻尼比越遠離5%，阻尼調整系數的離散程度越大.

圖3為阻尼比ξ=0.5%，3%，7%和30%時，不同矩震級分組的阻尼調整系數中值隨周期的變化情況.由圖3可知，矩震級對阻尼調整系數中值的影響與周期和阻尼比有關：在T<～0.6 s的范圍內，當ξ<5%時，阻尼調整系數中值隨周期的增加而線性增加；當ξ>5%時，阻尼調整系數中值隨周期的增加而線性減小；在該范圍內，矩震級對阻尼調整系數中值無顯著影響，各周期點處的阻尼調整系數中值基本相同.在T>～0.6 s的范圍內，當阻尼比ξ<5%時，阻尼調整系數中值隨周期的增大而減小，減幅隨矩震級的增大而趨緩，各周期點處的阻尼調整系數中值隨矩震級的增大而增大；當ξ>5%時，阻尼調整系數中值隨周期的增大而增大，增幅隨矩震級的增大而趨緩，各周期點處的阻尼調整系數中值隨矩震級的增大而減小；阻尼比越遠離5%，上述現象越明顯.圖4給出了T=3 s時，分別在阻尼比ξ=0.5%，2%，10%和20%處，矩震級與阻尼調整系數之間的散點圖.圖4中直線為矩震級和阻尼調整系數的線性擬合線，其斜率表明了矩震級對阻尼調整系數的影響程度.此外，由圖4可見，阻尼調整系數相對于阻尼比存在異方差性.由圖4與圖2e～h的直線斜率對比可知，矩震級對阻尼調整系數的影響程度與D5-95對其的影響程度基本相當.

3.3斷層距的影響

工程中一般采用震源距、震中距或斷層距來考慮地震波傳播途徑對地震動的影響.本文采用斷層距來考慮傳播途徑的影響，采用的斷層距為觀測點到斷裂面的最近距離Rrup.

為了研究斷層距Rrup對阻尼調整系數的影響，本文將地面運動記錄按斷層距Rrup分為3組見表2.

圖5為阻尼比ξ=0.5%，3%，7%和30%時，不同斷層距Rrup的阻尼調整系數中值隨周期的變化情況.由圖5可知，Rrup對阻尼調整系數中值的影響與周期和阻尼比有關：在T<～0.6 s的范圍內或當阻尼比接近5%時如ξ=3%和7%時，Rrup對阻尼調整系數中值無顯著影響，各周期點處的阻尼調整系數中值基本相同；在T>～0.6 s的范圍內，當阻尼比ξ<5%且遠離5%時如ξ=0.5%時，各周期點處的阻尼調整系數中值隨Rrup的增大而增大；當ξ>5%且遠離5%時如ξ=30%時，各周期點處的阻尼調整系數中值隨Rrup的增大而減小.與矩震級對阻尼調整系數中值的影響相比，Rrup對阻尼調整系數中值的影響較弱.

圖6給出了T=3 s時，分別在阻尼比ξ=0.5%，2%，10%和20%處，Rrup與阻尼調整系數之間的散點圖.圖6中直線為Rrup和阻尼調整系數的線性擬合線，其斜率表明了Rrup對阻尼調整系數的影響程度.此外，由圖6可見，阻尼調整系數相對于阻尼比存在異方差性.將圖6中的直線斜率分別與圖2e～h和圖4中的直線斜率對比可知，與D5-95和矩震級對阻尼調整系數的影響相比，Rrup對阻尼調整系數的影響較弱.3.4場地類別的影響

為了研究場地類別對阻尼調整系數的影響，本文按ASCE 7-1024中的場地分類標準將場地分為A， B，C，D和E 五類，各類場地與我國《建筑抗震設計規范》GB 50011-2010中的場地類別的對應關系可參見文獻25.地面運動記錄按場地類別的分組見表3.

表3基于平均剪切波速的地面運動記錄分組

由于A類場地上的記錄較少，表3中將A和B類場地上的記錄歸為一組；E類場地上的記錄過少，統計分析時未予考慮.圖7為阻尼比ξ=0.5%，3%，7%和30%時，不同場地類別的阻尼調整系數中值隨周期的變化情況.由圖7可知，場地類別對阻尼調整系數中值的影響與周期和阻尼比有關：在T<～0.6 s的范圍內或當阻尼比接近5%時如ξ=3%和7%時，場地類別對阻尼調整系數中值無顯著影響，各周期點處的阻尼調整系數中值基本相同；在T>～0.6 s的范圍內，當阻尼比ξ<5%且遠離5%時如：ξ=0.5%時，各周期點處的阻尼調整系數中值隨地表厚度30 m內平均剪切波速Vs，30的減小AB類場地變化到D類場地而增大；當ξ>5%且遠離5%時如：ξ=30%時，各周期點處的阻尼調整系數中值隨Vs，30的減小AB類場地變化到D類場地而減小.與矩震級對阻尼調整系數中值的影響相比，場地類別對阻尼調整系數中值的影響較弱.

圖8給出了T=3 s時，分別在阻尼比ξ=0.5%，2%，10%和20%處，地表厚度30 m內平均剪切波速Vs，30與阻尼調整系數之間的散點圖.圖8中直線為Vs，30和阻尼調整系數的線性擬合線，其斜率表明了Vs，30對阻尼調整系數的影響程度.此外，由圖8可見，阻尼調整系數相對于阻尼比存在異方差性.將圖8中的直線斜率分別與圖2e～h和圖4中的直線斜率對比可知，與D5-95和矩震級對阻尼調整系數的影響相比，場地類別對阻尼調整系數的影響較弱.4考慮矩震級影響的阻尼調整系數模型

根據以上分析，持時和矩震級對阻尼調整系數影響顯著，而斷層距和場地類別對阻尼調整系數的影響較弱，可忽略，因此合理的阻尼調整系數模型應能體現持時和矩震級的影響.由于在目前所使用的位移譜衰減模型15-19中均未包含持時這個參數，為便于工程應用，本文在阻尼調整系數模型中僅考慮矩震級這個變量，并通過矩震級與持時的相關性來間接考慮持時的影響.

4.1不考慮矩震級影響的阻尼調整系數殘差隨矩

震級的分布

為了確定考慮矩震級影響的阻尼調整系數模型，本文首先計算了不考慮矩震級影響的阻尼調整系數的殘差，作出殘差隨矩震級的分布，然后根據其分布來確定阻尼調整系數回歸方程的形式.殘差采用式

圖9僅給出了在T=0.1 s和3 s處，ξ=2%和20%時，殘差相對于矩震級的分布，在T<～0.6 s范圍內，各周期點處的殘差隨矩震級的分布與T=0.1 s處基本相同；在T>～0.6 s范圍內，各周期點處的殘差隨矩震級的分布趨勢與T=3 s處基本相同；以下類同，不再贅述.圖中實心方點代表每組殘差的均值，實線為均值的連線，表明了殘差隨矩震級的變化趨勢.由圖9可知，在T=0.1 s處，各阻尼比下的殘差基本隨機對稱地分布于零水平線的兩側，這表明了在T<～0.6 s范圍內矩震級對阻尼調整系數沒有顯著的影響；在T=3 s處，各阻尼比下的殘差相對于矩震級近似呈直線分布，表明在T>～0.6 s范圍內矩震級對阻尼調整系數有顯著的影響.可見，通過殘差分析所反映的矩震級對阻尼調整系數的影響與前文的分析結果是一致的.各參數估計值列于表4.根據表4、式6和式4可求得在ξj和Ti處每個數據與包含了線性震級項的回歸方程的殘差，然后可作出殘差相對于矩震級的分布.圖10為在T=0.1 s和3 s處，ξ=2%和20%時， 殘差相對于矩震級的分布.對比圖9和圖10可知：在T=0.1 s處，殘差相對于矩震級的分布與不考慮矩震級影響時基本相同，再次說明了T<～0.6 s范圍內矩震級對阻尼調整系數無顯著影響，各阻尼比的殘差隨機對稱地分布于零水平線的兩側；在T=3 s處，殘差相對于矩震級不再具有直線分布，各阻尼比下的殘差隨機對稱地分布于零水平線的兩側見圖10，這說明本文回歸模型的合理性且能反映出在T>～0.6 s范圍內矩震級對阻尼調整系數的影響.圖11為在ξ=0.5%和30%處，按式6取Mw=5.5，6.5和7.5所計算的阻尼調整系數中值與表1中分組Ⅰ，Ⅱ和Ⅲ所計算的阻尼調整系數中值的對比.由圖11可見，兩者吻合得較好且本文模型能體現矩震級對阻尼調整系數中值隨周期變化趨勢的影響.式11中，阻尼比取百分號中的整數如阻尼比為2%，取ξ=2.在每個周期點處，采用SPSS統計分析軟件進行非線性回歸分析，可得到每個周期點處a0～a3各參數的估計值見表4.圖12給出了在T=0.1 s和3 s處，標準差估計值與阻尼比之間的關系及式11的擬合結果，由圖可見擬合結果較好，且式11能合理地反映阻尼調整系數相對于阻尼比的異方差性.

12

式中：ε為隨機誤差且ε～N0， σ2lnDSF，σlnDSF的估計值采用式11計算.式11 和式12中各參數的估計值列于表4.該模型比僅考慮阻尼比和周期影響的阻尼調整系數更合理可靠，且可直接用于阻尼比為5%的位移譜衰減模型，以獲得其余阻尼比下的譜衰減模型.此外，本文所提出的模型也可為相關規范如《建筑抗震設計規范》等的制訂和修改提供參考.

圖14為在T=0.1 s和3 s處，ξ=2%和20%時，式6的殘差相對于D5-95的分布.對比圖13和圖14可知：在T=0.1 s處，殘差相對于D5-95的分布與不考慮矩震級影響時基本相同，再次說明在短周期范圍內D5-95對阻尼調整系數無顯著影響，各阻尼比的殘差隨機對稱地分布于零水平線的兩側；在T=3 s處，本文提出的包含線性矩震級項的回歸

方程極大地改善了該處殘差相對于D5-95的分布，使得殘差相對于D5-95不再呈曲線分布，殘差基本隨機對稱地分布于零水平線的兩側，說明了本文模型能體現短周期范圍外地震動持時對阻尼調整系數的影響.

根據以上分析，由于矩震級與地震動持時的強相關性，本文所提出的包含線性矩震級項的阻尼調整系數模型能體現地震動持時對阻尼調整系數的影響.此外，由于譜衰減模型15-19中通常都包含了矩震級這個參數，所以本文模型更便于工程運用.

6結論

基于408條地震地面運動記錄，研究了地震動持時、矩震級、斷層距和場地類別對位移譜阻尼調整系數的影響，并在此基礎上提出了能體現地震動持時和矩震級影響的阻尼調整系數回歸模型，得出以下結論：

1相對能量持時D5-95和矩震級對阻尼調整系數的影響與周期和阻尼比有關.在短周期范圍內，D5-95和矩震級對阻尼調整系數無顯著影響.在短周期范圍外，D5-95和矩震級對阻尼調整系數的影響顯著；當ξ<5%時，阻尼調整系數隨D5-95和矩震級的增加而增加；當ξ>5%時，阻尼調整系數隨D5-95和矩震級的增加而減小；阻尼比越遠離5%，上述阻尼調整系數隨D5-95和矩震級變化的趨勢越顯著.

2在短周期范圍內，觀測點到斷層面的最近距離Rrup和場地類別Vs，30對阻尼調整系數均無顯著影響.在短周期范圍外，當ξ<5%時，阻尼調整系數隨Rrup的增加或隨Vs，30的減小而增加，當ξ>5%時，阻尼調整系數隨Rrup的增加或隨Vs，30的減小而減小，但與持時和矩震級的影響相比，Rrup和Vs，30的影響較弱.

3阻尼調整系數相對于阻尼比存在異方差性；阻尼比越遠離5%時，阻尼調整系數的離散程度越大.

4本文所提出的包含線性震級項的回歸方程能體現矩震級和地震動持時對阻尼調整系數的影響，且模型的方差能體現阻尼調整系數相對于阻尼比的異方差性.

5本文的研究結果可直接用于阻尼比為5%的位移譜衰減模型，也可為我國抗震設計規范的制訂和修改提供參考.

參考文獻

1NEWMARK N M， HALL W J. Earthquake spectra and design M. Oakland： Earthquake Engineering Research Institute， 1982： 35-36.

2WU J， HANSON R D. Study of inelastic spectra with high damping J. Journal of Structural Engineering， 1989， 1156：1412-1431.

3IDRISS I M. Procedures for selecting earthquake ground motions at rock sites R.Washington， DC： National Institute of Standards and Technology， 1993： 2-3.

4ASHOUR S A. Elastic seismic response of buildings with supplemental damping D. Ann Arbor： University of Michigan， 1987： 24-29.

5TOLIS S V， FACCIOLI E. Displacement design spectra J. Journal of Structural Engineering， 1999， 31： 107-125.

6GB 50011—2001 建筑抗震設計規范S. 北京：中國建筑工業出版社， 2001：28-29.

GB 50011—2001 Code for seismic design of buildings S. Beijing： China Architecture and Building Press， 2001： 28-29.In Chinese

7GB 50011—2010 建筑抗震設計規范S. 北京：中國建筑工業出版社， 2010：33-35.

GB 50011—2010 Code for seismic design of buildings S. Beijing： China Architecture and Building Press， 2010： 33-35.In Chinese

8胡聿賢. 地震工程學 M. 北京：地震出版社，2006：135-138.

HU Yuxian. Earthquake engineering M. Beijing： Seismological Press， 2006： 135-138.In Chinese

9王曙光，杜東升，劉偉慶， 等. 隔震結構不同阻尼比地震影響系數曲線的改進研究 J. 建筑結構學報，2009， 303：112-119.

WANG Shuguang， DU Dongsheng， LIU Weiqing， et al. Research on seismic influence coefficient of seismic isolated structure with different damping ratio J. Journal of Building Structures， 2009， 303 ： 112-119. In Chinese

10曹加良，施衛星，汪洋， 等. 我國抗震設計規范設計反應譜及譜阻尼折減系數研究 J. 建筑結構學報，2011，329：34-43.

CAO Jialiang， SHI Weixing， WANG Yang， et al. Study on spectra and spectral damping reduction factors in Chinese seismic design codes J. Journal of Building Structures，2011， 329 ： 34-43.In Chinese

11LIN Y Y， CHANG K C. Effects of site class on damping reduction factors J.Journal of Structural Engineering， 2004 ， 13011：1667-1675.

12BOMMER J J， MENDIS R. Scaling of spectral displacement ordinates with damping ratios J. Earthquake Engineering and Structural Dynamics， 2005， 342：145-165.

13CAMERON W I， GREEN I. Damping correction factors for horizontal ground motion response spectra J. Bulletin of the Seismological Society of America， 2007， 973： 934-960.

14STAFFORD P J， MENDIS R， BOMMER J J. Dependence of damping correction factors for response spectra on duration and numbers of cycles J. Journal of Structural Engineering， 2008， 1348： 1364-1373.

15ABRAHAMSON N A， SILVA W J. Summary of the Abrahamson & Silva NGA ground motion relations J. Earthquake Spectra， 2008， 241： 67-97.

16BOORE D M， ATKINSON G M. Groundmotion prediction equations for the average horizontal component of PGA， PGV， and 5% damped PSA at spectral periods between 0.01 s and 10 s J. Earthquake Spectra， 2008， 241：99-138.

17CAMPBELL K W， BOZORGNIA Y. NGA ground motion model for the geometric mean horizontal component of PGA， PGV， PGD， and 5% damped linear elastic response spectra for periods ranging from 0.01s to 10.0s J. Earthquake Spectra， 2008， 241：139-171.

18CHIOU B S，YOUNGS R R. An NGA model for the average horizontal component of peak ground motion and response spectraJ. Earthquake Spectra， 2008， 241：173-215.

19IDRISS I M. An NGA empirical model for estimating the horizontal spectral values generated by shallow crustal earthquakes J. Earthquake Spectra， 2008， 241：217-242.

20KEMPTON J J， STEWART J P. Prediction equations for significant duration of earthquake ground motions considering site and nearsource effectsJ.Earthquake Spectra， 2006， 224：985-1013.

21謝禮立，張曉志. 地震動記錄持時和工程持時J. 地震工程與工程振動，1988， 81：31-38

XIE Lili， ZHANG Xiaozhi. Accelerogrambased duration and engineering duration of ground motion J. Earthquake Engineering and Engineering Vibration，1988， 81：31-38.In Chinese

22JAYARAM N， BAKER J W. Statistical tests of the joint distribution of spectral acceleration values J. Bulletin of the Seismological Society of America， 2008， 985： 2231-2243.

23ARIAS A. A measure of earthquake intensity in seismic design for nuclear power plants R. Cambridge， MA： MIT Press， 1970： 438-468.

24ASCE 7-10. Minimum design loads for buildings and other structures S. Washington， DC： American Society of Civil Engineers， 2010： 203-205.

25郝安民，周德源，李亞明，等. 考慮震級影響的規范阻尼修正系數評估J. 同濟大學學報，2012， 405： 657-661.

HAO Anmin， ZHOU Deyuan， LI Yaming， et al. Evaluation of damping modification factors in codes with a consideration of effect of earthquake magnitudeJ. Journal of Tongji University，2012， 405： 657-661.In Chinese

26ANG A HS， TANG W H. Probability concepts in engineering planning and design： Volume 1 basic principlesM. New York： John Wily & Sons，Inc， 1975： 297-300.