基于自回歸模型的基坑周邊建筑物沉降預(yù)測分析

劉小強(qiáng)

（河南工程學(xué)院，河南 鄭州 451191）

自回歸模型是一種優(yōu)秀的動態(tài)分析方法，可用于預(yù)測變化趨勢［1］。在模型建立后，需對模型進(jìn)行檢驗(yàn)分析，且必須對模型的預(yù)測結(jié)果進(jìn)行驗(yàn)證，以確保其適用性。

1 基坑周邊建筑物沉降監(jiān)測

1.1 基準(zhǔn)點(diǎn)

基準(zhǔn)點(diǎn)可以埋設(shè)在開挖影響區(qū)外的原狀土中，或在一個穩(wěn)定的建筑結(jié)構(gòu)上。由于固定的基準(zhǔn)點(diǎn)通常用來確定整個沉降監(jiān)測基準(zhǔn)，應(yīng)該采用高等級的水準(zhǔn)網(wǎng)，整個觀測也應(yīng)采用高標(biāo)準(zhǔn)進(jìn)行。觀測應(yīng)采用高精度的光學(xué)或電子水準(zhǔn)儀進(jìn)行。

1.2 精度要求和沉降監(jiān)測方法

不同的項(xiàng)目和現(xiàn)場條件，對沉降監(jiān)測的精度要求不同。對基坑周邊建筑物沉降監(jiān)測的目的是為了及時獲得沉降信息，并根據(jù)其沉降速度確定建筑物是否穩(wěn)定。沉降速度標(biāo)準(zhǔn)，由設(shè)計(jì)師或相關(guān)規(guī)范給出，如某棟建筑物沉降觀測，當(dāng)其沉降量高于0.04mm/d，說明建筑物是不穩(wěn)定的［2］。因此，要真正確定建筑物沉降量和穩(wěn)定性，必須使用精密水準(zhǔn)測量方法。

2 自回歸模型預(yù)測方法

假設(shè)連續(xù)沉降監(jiān)測樣本的平穩(wěn)序列為

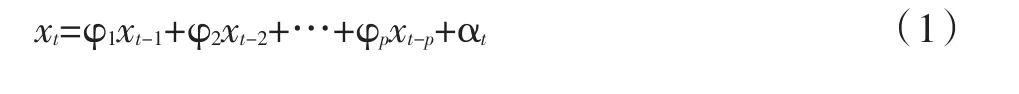
對于時間節(jié)點(diǎn)tj和tk，相應(yīng)的序列是xj和xk。

時間差τ變量之間的自相關(guān)函數(shù)的估計(jì)值可表示為

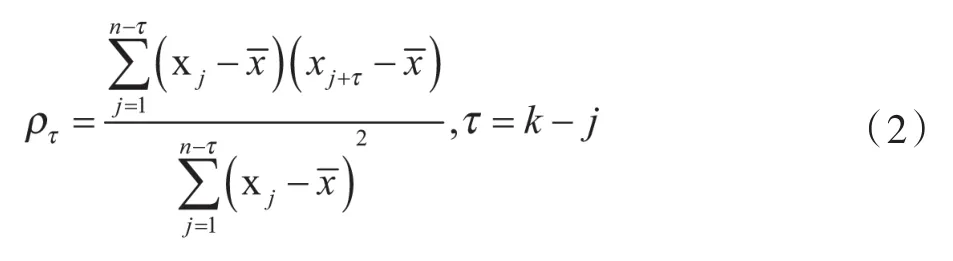
依據(jù)自相關(guān)函數(shù)，自回歸參數(shù)φ的估計(jì)值可通過方程（3）獲得：

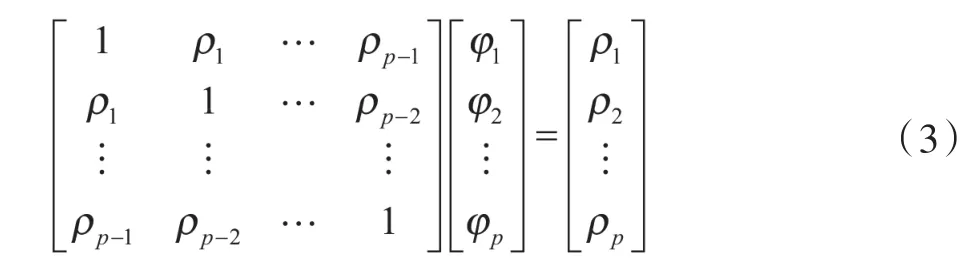
由自回歸參數(shù)可以確定自回歸模型的AR（p）：

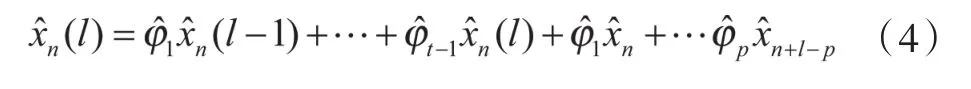
根據(jù)在時間節(jié)點(diǎn)n得到的數(shù)據(jù)和前期數(shù)據(jù)，下面的模型可用于預(yù)測

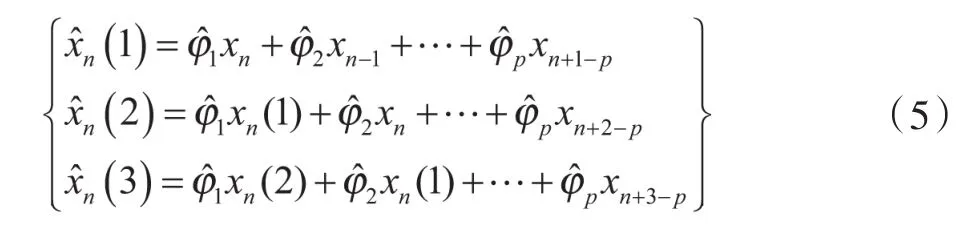
3 沉降預(yù)測

實(shí)驗(yàn)選擇了某深基坑周邊的一棟高層建筑物。在遠(yuǎn)離基坑的外部，選擇了三個基準(zhǔn)點(diǎn)，形成閉合水準(zhǔn)路線。采用二級水準(zhǔn)，確定了基準(zhǔn)點(diǎn)的數(shù)據(jù)，且每周對基準(zhǔn)點(diǎn)進(jìn)行穩(wěn)定性分析。在基坑開挖階段，對該建筑物連續(xù)的進(jìn)行了沉降監(jiān)測。表1列出了某一測量點(diǎn)16期的高程觀測值。

如表1所示，數(shù)值有一些波動，但總的趨勢是降低。使用16期的觀測數(shù)據(jù)，估計(jì)自相關(guān)函數(shù)和偏相關(guān)函數(shù)的前六項(xiàng)，見表2。

如表2中所示，自相關(guān)函數(shù)的變化沒有明顯的截尾特征，而偏自相關(guān)函數(shù)顯示了明顯的截尾特征，取閾值為0.5，可以確定自回歸模型為模型AR（1）。

利用第17-20期的數(shù)據(jù)進(jìn)行預(yù)測，結(jié)果見表3。

如表3所示，使用AR（1）模型預(yù)測的最大殘差為0.6毫米，表現(xiàn)出良好的精度。說明該自回歸模型適用于這座大樓的沉降預(yù)測。在整個基坑的施工期，當(dāng)獲得一定量的觀測數(shù)據(jù)后，就可以進(jìn)行沉降預(yù)測。為了提高預(yù)測精度，應(yīng)及時納入增加的觀測數(shù)據(jù)來校正模型。

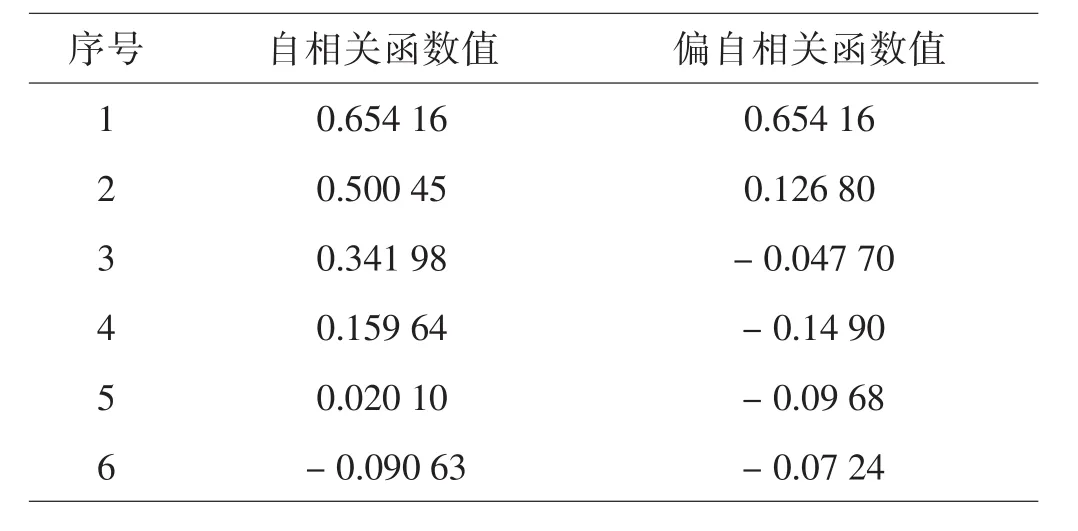
表2 自相關(guān)函數(shù)值和偏自相關(guān)函數(shù)值

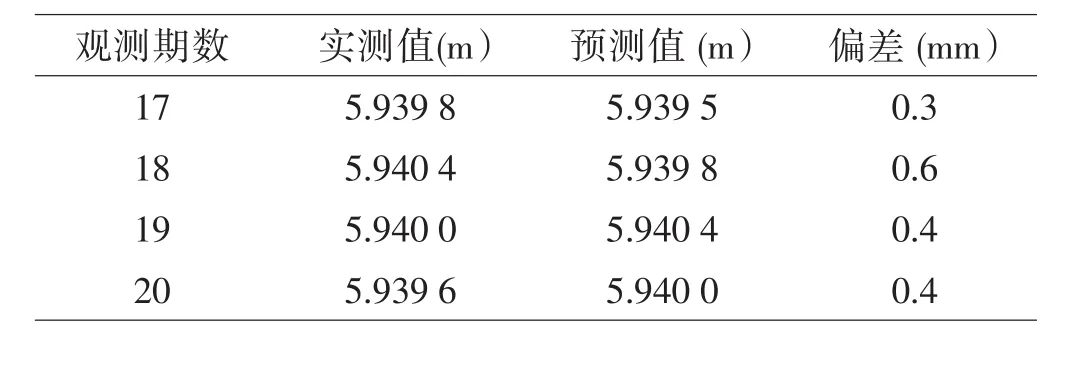
表3 沉降預(yù)測結(jié)果

4 結(jié)語

①應(yīng)首先用統(tǒng)計(jì)檢驗(yàn)方法對建筑物沉降監(jiān)測基準(zhǔn)的穩(wěn)定性進(jìn)行分析，從而在源頭上確保觀測數(shù)據(jù)的有效性。

②為了真實(shí)地反映建筑物沉降變化和正確的趨勢預(yù)測，沉降監(jiān)測數(shù)據(jù)的精度必須滿足要求。

③構(gòu)建自回歸模型AR（P）必須有相應(yīng)的樣本，且樣本的特征需滿足相應(yīng)的要求。一般根據(jù)估計(jì)的自相關(guān)函數(shù)和偏自相關(guān)函數(shù)的特征來確定模型的類型和階數(shù)。對建立的模型必須進(jìn)行驗(yàn)證，以確保其適用性。

④自回歸模型，隨著樣本的不同模型就會不同，也就是說模型是特定的，不能隨意類推使用。

［1］何秀鳳，華錫生，等.GPS一機(jī)多天線變形監(jiān)測系統(tǒng)［J］.水電自動化與大壩監(jiān)測，2002（2）：38-39.

［2］王琪，游新兆，王啟梁.用全球定位系統(tǒng)(GPS）監(jiān)測青藏高原地殼形變［J］.地震地質(zhì)，1996（12）：121-122.