執行器飽和的線性連續系統的鎮定

杜鴻波　景麗

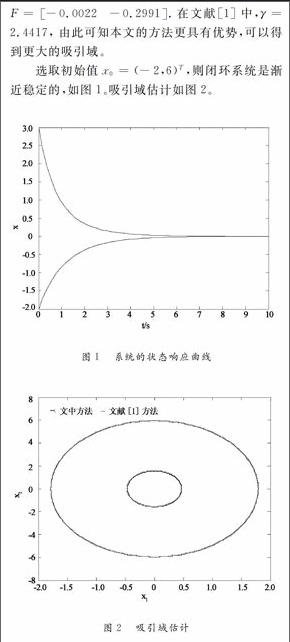
摘 要：針對控制系統中廣泛存在飽和問題，主要研究執行器飽和線性連續系統的鎮定問題并進行吸引域估計。首先根據Finslers 引理和Lyapunov 函數方法研究系統穩定的充分條件，得到執行器飽和控制系統穩定的新判據。其次，在穩定條件下，應用凸組合方法和新引入的自由權矩陣使得系統吸引域估計具有更小的保守性，將所得非線性矩陣不等式轉化為線性矩陣不等式，給出求解最大吸引域的優化方法和狀態反饋控制器的設計方案。最后通過仿真算例驗證結果的有效性和可行性。

關鍵詞：連續系統；執行器飽和；吸引域估計；線性矩陣不等式

中圖分類號：O231 文獻標識碼：A

Abstract：Aiming at the saturation which plays important roles in the control theory，this paper studied the problem of stabilization of linear continuous time system with actuator saturation， and estimated the domain of attraction of the system. First，by using Finsler 's lemma and Lyapunov equation method to study the stability condition of the system， we get the new criterion of the stability of the actuator saturation control system. In addition， under the condition of stability，by using convex combination method and the newly introduced liberty matrix，this paper reduced the conservatism of the estimation of domain of attraction. By converting the nonlinear matrix inequality to linear matrix inequality， the optimization method of the biggest domain of attraction and the design scheme of the state feedback controller were presented. Finally， the simulation example verifies the feasibility and effectiveness of the results.

Key words：continuous system；actuator saturation；estimation of domain of attraction；linear matrix inequality

1 引 言

飽和現象廣泛地存在于各種工業系統當中，對實際工程來說，控制往往屬于容許控制集合，即控制輸入需要滿足一定的約束條件，執行器飽和限制是一種最常見的約束控制，所以對于這類問題的研究自然就有非常重要的意義。1964年A.T.Fuller首次提出飽和系統，上個世紀90年代，學者們對飽和系統的理論研究熱情高漲，取得了豐碩的成果。

近幾年，Hu等針對狀態反饋下的飽和系統，利用飽和非線性的特性，提出了凸組合的處理方法，通過引入輔助矩陣H，處理飽和非線性項[1，2]。Cao和Lin基于飽和關聯函數，給出了線性離散系統的穩定性判據，應用線性矩陣不等式計算最大吸引域[3]。Ma和Yang根據Finslers引理，得到了線性離散執行器飽和控制系統穩定性新方法，并通過迭代算法進行吸引域估計[4]。朱發旺等人基于飽和關聯函數研究了線性離散時間系統的吸引域估計問題，通過為每一個橢球尋找輔助的增益矩陣來降低吸引域估計的保守性[5]。陳奇等采用時變的二次Lyapunov函數，對線性離散飽和系統進行穩定性分析及吸引域估計，得到了最大吸引域的優化方法[6]。對于線性連續執行器飽和控制系統，Zou和Wang 通過對Lyapunov方程的模型轉換，給出了一種改進的穩定條件，并且進行了吸引域估計[7]。Guan和Yang基于錐互補的線性化程序給出了動態輸出反饋控制器的設計方法[8]。Shi等應用仿射的飽和關聯Lyapunov函數對系統進行吸引域估計，得到了較好的結果[9]。

本文將研究執行器飽和問題，根據Finslers引理給出穩定條件的新判據，并進行吸引域估計。

6 結 論

本文基于Lyapunov函數方法和Finslers引理，通過引入輔助自由矩陣給出了線性連續控制系統的穩定條件的新判據，進一步可求解最大吸引域，所得結果具有更小的保守性。

參考文獻

[1] Hu Tingshu， Lin Zongli， CHEN B M. An analysisand design method for linear systems subject to actuator saturation and disturbance[J]. Automatica， 2002， 38（2）： 351-359.

[2] Hu Tingshu， Lin Zongli， CHEN B M. Analysis and Design for Discrete-time Systems Subject to Actuator Saturation [J]. Systems & Control Letters， 2002， 45（2）： 97-112.

[3] Cao Yongyan， Lin Zongli. Stability analysis of discrete-time systems with actuator saturation by a saturation-dependent Lyapunov function[J].Automatica， 2003， 39（7）： 1235-1241.

[4] Ma Yongmei ， Yang Guanghong . Stability analysis for linear discretetime systems Subject to actuator saturation[J]. J Control Theory Appl ， 2010， 8（2）：245-248.

[5] 朱發旺， 黃騰云， 劉和光， 等. 基于飽和關聯 Lyapunov 函數的飽和離散系統吸引域估計[J].江南大學學報：自然科學版， 2011， 10 （4）：379-384.

[6] 陳奇，倪偉，王林高.線性離散飽和系統穩定性分析及吸引域估計[J]. 控制工程，2012， 19（S1）： 161-164， 171.

[7] Zou Zhiqiang， Wang Yijing. On enlarging thedomain of attration for nlinear systems subject toactuator saturation[J]. Internation Journal ofGeneral Systems， 2008， 37（2）： 239-248.

[8] Guan Wei， Yang Guanghong. Analysis and designof output feedback control systems with actuatorsaturation[J]. Journal of Control Theory and Applications， 2008， 6（4）： 421-426.

[9] Shi Ting ， Su Hongye ， Chu Jian. Stability analysis for continuoustime systems with actuator saturation.[J]. Journal of Control Theory and Applications2009 ，7（4）： 352–358.

[10]俞立. 魯棒控制線性矩陣不等式處理方法[M].北京： 清華大學出版社， 2002.