科學(xué)選題，有效訓(xùn)練——藝術(shù)生有效復(fù)習(xí)三角函數(shù)專題探究

朱華仙

（浦江職業(yè)技術(shù)學(xué)校）

縱觀近幾年的高考命題特點，結(jié)合《2015年浙江考試說明》，根據(jù)我校藝術(shù)生的實際，我們高三備課組經(jīng)過仔細討論研究近五年的高考試題，確定了三角函數(shù)專題的重點和難點.

專題重點：三角函數(shù)的小題重點在基礎(chǔ)知識：三角函數(shù)的概念、運用三角函數(shù)的關(guān)系化簡與求值、三角函數(shù)的圖象和性質(zhì)、和差角公式、三角函數(shù)符號規(guī)律、二倍角公式等；大題重點主要是三角函數(shù)的圖象和性質(zhì)、三角恒等變換、解三角形等.

專題難點：小題難點是三角函數(shù)圖像變換、性質(zhì)（即單調(diào)性、對稱性、奇偶性、周期性）的綜合應(yīng)用、靈活應(yīng)用正余弦定理，三角形內(nèi)角和定理和面積公式等解三角形.

突破考點：因三角函數(shù)內(nèi)容難度不是很大，方法靈活多樣，基礎(chǔ)較好的藝術(shù)生都會有解題思路，所以上課講例題時我盡量先讓學(xué)生自己動手解，再和全班同學(xué)一起討論總結(jié)部分能解出題目的學(xué)生的解法，再一起找出最簡解法，并加以適當(dāng)補充，師生共同歸納出一種最美解法。本專題主要給藝術(shù)生確定的熱點問題有以下幾個方面.

熱點一：運用三角函數(shù)的關(guān)系化簡或求值

考點剖析：本題考查了誘導(dǎo)公式、三角函數(shù)的符號規(guī)律、同角三角函數(shù)的關(guān)系式，對數(shù)基本運算法則.先利用誘導(dǎo)公式和對數(shù)運算法則求出sinα，再由α 的范圍、誘導(dǎo)公式和平方關(guān)系求出cos（2π-α）.

考點剖析：本題考查同角三角函數(shù)關(guān)系、三角函數(shù)的符號規(guī)律、兩角和與差的三角函數(shù)。注意觀察找出關(guān)系，根據(jù)題中所給的范圍得所以由平方關(guān)系并注意符號規(guī)律就可求出再利用差角公式求得答案.

考點剖析：本題主要考查同角三角函數(shù)關(guān)系，三角函數(shù)符號，特殊角三角函數(shù)值等.

把原式平方得（sinα-cosα）2=2，所以sin2α=-1，根據(jù)題中α 的范圍，可得

總結(jié)規(guī)律：

1.利用同角關(guān)系和誘導(dǎo)公式解題時特別要注意象限角對三角函數(shù)符號的影響；

2.在三角函數(shù)式求值化簡時，注意平方關(guān)系和弦切互化公式的變形應(yīng)用；

3.靈活運用和積轉(zhuǎn)換法進行變形、化簡，如：（sinα±cosα）2=1±2sinαcosα 等；

【課堂跟蹤訓(xùn)練】

熱點二：三角函數(shù)的圖象和性質(zhì)

例2.（1）（2012·浙江）把函數(shù)y＝cos2x＋1的圖象上所有點的橫坐標(biāo)伸長到原來的2倍（縱坐標(biāo)不變），然后向左平移1個單位長度，再向下平移1個單位長度，得到的圖象是 （ ）

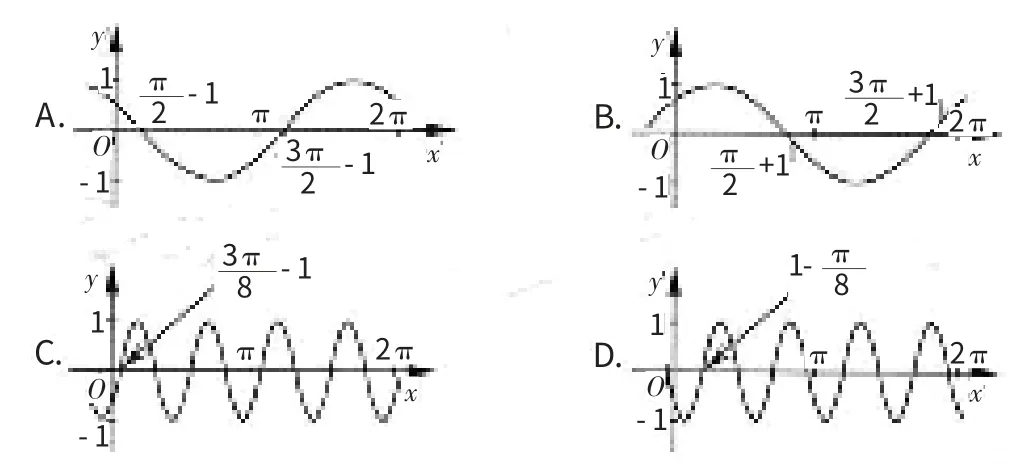
考點剖析：三角變換是三角函數(shù)圖象內(nèi)容的一個重要考點。把函數(shù)y＝cos2x＋1的圖象上所有點的橫坐標(biāo)伸長到原來的2倍（縱坐標(biāo)不變）得y1＝cosx＋1，向左平移1個單位長度得y2＝cos（x+1）+1，再向下平移1個單位長度得y3＝cos（x+1），觀察圖象即得答案A．

（2）（2013·浙江）函數(shù)f（x）=sinxcosx+的最小正周期和振幅分別是 （ ）

考點剖析：本題考查三角函數(shù)的圖象與性質(zhì)、二倍角公式、和差角公式等。熟練掌握公式是解本題的關(guān)鍵.先利用二倍角公式化簡f（x）解析式，再利用和差角公式化為一個角的正弦函數(shù)，根據(jù)解析式確定出振幅，找出ω 的值，再由求出函數(shù)的最小正周期。即f（x，∵-1≤sin（2x+≤1，∴振幅為1，∵ω=2，∴T=π．

（3）（2014·浙江）為了得到函數(shù)y=sin3x+cos3x的圖象，可以將函數(shù)的圖象 （ ）

考點剖析：本題考查三角函數(shù)圖象的平移變換性質(zhì)，和差角公式化簡等.平移變換中注意x的系數(shù).先化簡，再由“左加右減”法則得到答案C.

規(guī)律總結(jié)：

1.求三角函數(shù)的最小正周期時，一定要先化簡解析式為只含一個三角函數(shù)的式子，即化為“y=Asin（ωx+ψ），y=Acos（ωx+ψ）,y=Atan（ωx+ψ）”的形式，再利用周期公式求解；

2.求三角函數(shù)的最值時，一定要注意自變量的取值范圍，最大和最小值不一定在自變量區(qū)間的端點處取得,一定要結(jié)合三角函數(shù)圖象；

3.三角函數(shù)圖象進行平移變換時一定要注意提取x的系數(shù)，周期變換的時候要將x的系數(shù)變?yōu)樵瓉淼摩?倍.

【課堂跟蹤訓(xùn)練】

2.（2013·四川卷）已知函數(shù)f（x）＝2sin（ωx＋Φ）的部分圖象如圖所示，則ω，Φ 的值分別是（ ）

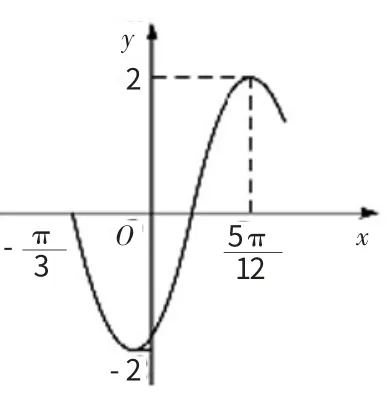
3.（2014·鎮(zhèn)海）設(shè)函數(shù)f（x）=sin（-2x+ψ）（0<ψ<π），y=f（x）的一條對稱軸是直線，（1）求ψ；（2）求函數(shù)y=f（x）的單調(diào)區(qū)間.

熱點三：解三角形

例3.（1）（2013·浙江）在銳角△ABC中，內(nèi)角A，B，C的對邊分別為a，b，c，且

（Ⅰ）求角A的大小；

（Ⅱ）若a=6，b+c=8，求△ABC的面積．

考點剖析：本題考查三角函數(shù)求值，解三角形，正余弦定理的靈活應(yīng)用等，熟練掌握三角形的面積公式是本題的關(guān)鍵.（Ⅰ）先利用正弦定理化簡原式得

（Ⅱ）由余弦定理得：a2=b2+c2-2bc·cosA，即36=b2+c2-bc=（b+c）2-3bc=64-3bc

（2）（2013·重慶）在△ABC中，內(nèi)角A，B，C的對邊分別為a，b，c，且

（Ⅰ）求A的值；

考點剖析：本題主要考查正余弦定理，面積公式，三角恒等變換等.

（3）（2011·浙江）18.在△ABC中，角A、B、C所對的邊分別為a，b，c．已知sinA+sinC=psinB（p∈R）且

（Ⅱ）若角B為銳角，求p的取值范圍.

考點剖析：（Ⅰ）本題主要考查三角變換、正弦定理、余弦定理等基礎(chǔ)知識，同時考查基本運算求解能力。由題設(shè)并利用正弦定理，得

（Ⅱ）由余弦定理，b2=a2+c2-2accosB

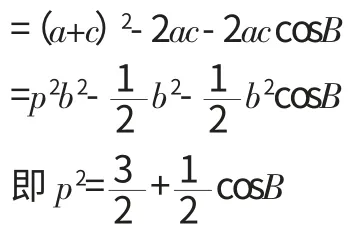
因為B為銳角，0＜cosB＜1，得由題設(shè)知p＞0，所以

規(guī)律總結(jié)：考查三角函數(shù)求值，解三角形，是近幾年高考解答題最常見題型.

1.在解三角形問題中，三角形內(nèi)角和定理起著重要作用，要注意確定角的限制范圍及三角函數(shù)值的符號，防止出現(xiàn)增解或漏解；

2.正余弦定理應(yīng)用時，應(yīng)注意靈活性，尤其邊角的互化，一般全部化為角的關(guān)系，或全部化為變的關(guān)系，可提醒學(xué)生一般題中若出現(xiàn)邊的一次式采用正弦定理，出現(xiàn)邊的二次式采用余弦定理；

3.碰到面積問題時要根據(jù)題意靈活選用面積公式.

【課堂跟蹤訓(xùn)練】

1.（2014·浙江）在△ABC中，內(nèi)角A，B，C所對的邊分別為a，b，c.已知

（I）求角C的大小；

（II）若b=4，△ABC的面積為6，求邊長c的值.

2.（2014·全國）已知a，b，c分別為△ABC的三個內(nèi)角A，B，C的對邊，a=2，且（2+b）（sinA-sinB）=（c-b）sinC，則△ABC面積的最大值為________.

3（.2013·山東卷）△ABC的內(nèi)角A，B，C的對邊分別為a，b，c，若B=2A，a=1，b=，則c= （ ）

三角函數(shù)專題是近些年高考試題中的熱點,因藝術(shù)生基礎(chǔ)較差，計算能力較弱，因此，課堂上要非常關(guān)注每個學(xué)生解題的易錯點，并及時指出，再跟蹤訓(xùn)練類型相似的試題，再總結(jié)此類題型的基本數(shù)學(xué)思想方法及解題應(yīng)試技巧等.本專題的復(fù)習(xí)，例題的選取很關(guān)鍵，我給藝術(shù)生練的每個題目都有明確的針對性和目的性，通過疏密有度的訓(xùn)練，提高藝術(shù)生的應(yīng)試技巧，全面提高藝術(shù)生綜合運用所學(xué)知識和方法分析問題和解決問題的基本能力，逐步培養(yǎng)他們的自主學(xué)習(xí)能力.