激波沖擊火焰的渦量特性研究*

朱躍進,董 剛

(1.江蘇大學能源與動力工程學院,江蘇 鎮江 212013; 2.南京理工大學瞬態物理重點實驗室,江蘇 南京 210094)

?

激波沖擊火焰的渦量特性研究*

朱躍進1,2,董 剛2

(1.江蘇大學能源與動力工程學院,江蘇 鎮江 212013; 2.南京理工大學瞬態物理重點實驗室,江蘇 南京 210094)

激波沖擊火焰的現象涉及一系列復雜的物理化學過程，其中渦量的生成與演化對控制火焰發展起重要作用。為系統分析激波沖擊火焰過程中的渦量特性，采用二維帶化學反應的Navier-Stokes方程對平面入射激波及其反射激波與球形火焰作用的現象進行了數值研究，通過引入并行計算達到高網格分辨率的要求。計算結果表明，斜壓項對火焰區內渦量生成起主導作用，壓縮項和耗散項在火焰膨脹階段抑制渦量生成，此外，火焰在激波壓縮階段主要受物理過程而非化學反應過程影響。

爆炸力學;渦量;Navier-Stokes方程;火焰;激波;斜壓項

激波沖擊火焰的現象常常出現在慣性約束聚變[1]、超聲速燃燒推進[2]和工業爆炸災害[3]等領域，涉及復雜的物理化學機制，相關研究有利于對激波-火焰作用現象的抑制或利用，因而具有重要的科學意義和應用價值。

G.H.Markstein[4]的經典實驗首次清晰顯示了火焰在弱激波及其反射激波作用下的變形失穩過程；英國Wales大學的G.O.Thomas等[5]實驗研究了平面激波沖擊球形火焰的過程，他們通過高速攝影發現，較強的入射激波及平面反射激波可使火焰形狀發生嚴重變形。與此同時，隨著計算機技術的發展，許多數值模擬工作得以開展。G.A.Bately等[6-7]數值研究了壓力波及其反射波與柱形火焰的相互作用過程，計算結果表明，當反射波與火焰作用時，黏性效應對變形火焰的渦量演化有較大影響；Y.Ju等[8]研究了不同強度的入射激波對火焰變形的影響，結果發現火焰區的總燃燒速率隨激波強度的增加而增加；美國海軍研究實驗室的E.S.Oran等[3]和A.M.Khokhlov等[9-11]對激波沖擊火焰的問題展開了一系列研究，認為Richtmyer-Meshkov(RM)不穩定性是火焰變形失穩的主要機制, 且變形火焰的燃燒速率和放熱率均有所提高，當條件適當時，反射激波與火焰的相互作用還會產生熱點和爆轟。本文作者[12-15]采用Navier-Stokes(NS)方程，考察了化學反應機理、網格尺寸、激波強度、化學反應活性、火焰表面積等不同因素對激波-火焰作用過程的影響，并通過可視化圖像、火焰積分量、火焰界面幾何特性等方面的分析來探討火焰變形、燃燒和混合等過程的變化規律及相互作用關系。

上述研究均表明，由于存在斜壓效應，激波沖擊火焰時可在火焰面處產生大量渦量，從而影響火焰界面變形、燃料與氧化劑混合、燃燒放熱等一系列物理化學現象，因此有必要深入研究激波沖擊火焰過程中的渦量特性，但目前尚缺乏對上述問題的系統研究。

本文中將采用高分辨率網格和基于MPI信息傳遞[16]的并行方法，開展入射及其反射激波與球形火焰多次作用的二維數值模擬，根據計算結果對變形火焰區域內的渦量特性進行深入分析研究，具體包括渦量演化過程、渦動力學分析、環量分析等，以期為理解激波沖擊火焰這一經典問題提供新的視角和思路。

1 數理模型與計算

1.1 數理模型

采用的二維帶化學反應的NS方程可表示為：

(1)

(2)

(3)

(4)

式中：ρ為密度；ui為i方向速度(i=1，2)；τij為黏性應力張量；E為單位體積總能量，E=p/(-1) ++ρqY；p為壓力；為比熱比；q為單位質量的總化學能；Y為反應物質量分數；qj為熱通量，qj=-kT/xj；為化學反應速率；熱傳導系數k、擴散系數D、運動學黏性υ 的表達見文獻[3]。

控制方程(1)～(4)采用分裂算法求解：空間導數項的無黏部分采用高精度五點TVD格式[13-15]計算，黏性部分采用二階空間中心差分計算，時間推進過程采用二階Runge-Kutta方法求解。本文采用單步化學反應來描述燃燒過程，相關化學反應熱力學和動力學參數可參見文獻[14]。

1.2 計算條件

計算以文獻[5]中的實驗為依據，設計如圖1所示的計算區域(灰色部分)與初始流場：計算區域流向(x)長0.17 m，法向(y)高0.038 m；球形火焰中心位于(x=0.035 m,y=0 m)處，初始時刻半徑R0=0.019 m，內部密度ρ1=15.78 g/m3；火焰外部反應性預混氣體組成為C2H4+3O2+4N2，密度ρ0=161.5 g/m3，初始溫度T0=293 K；火焰內外壓力均為p0=13.3 kPa；入射激波馬赫數為1.7，初始時位于x=0.012 m處，激波沿x方向從左向右傳播，當行至右端壁面后發生反射，左行的反射激波與火焰再次作用；激波后氣體狀態由Rankine-Hugoniot關系式給出。

數值計算采用的網格尺寸為47.5 μm×47.5 μm，因此本文中考慮的預混氣體在入射激波和反射激波作用后的火焰反應區寬度可分別由大約8個、3個網格來刻畫，網格尺寸足以精細反映火焰結構[12,15]。

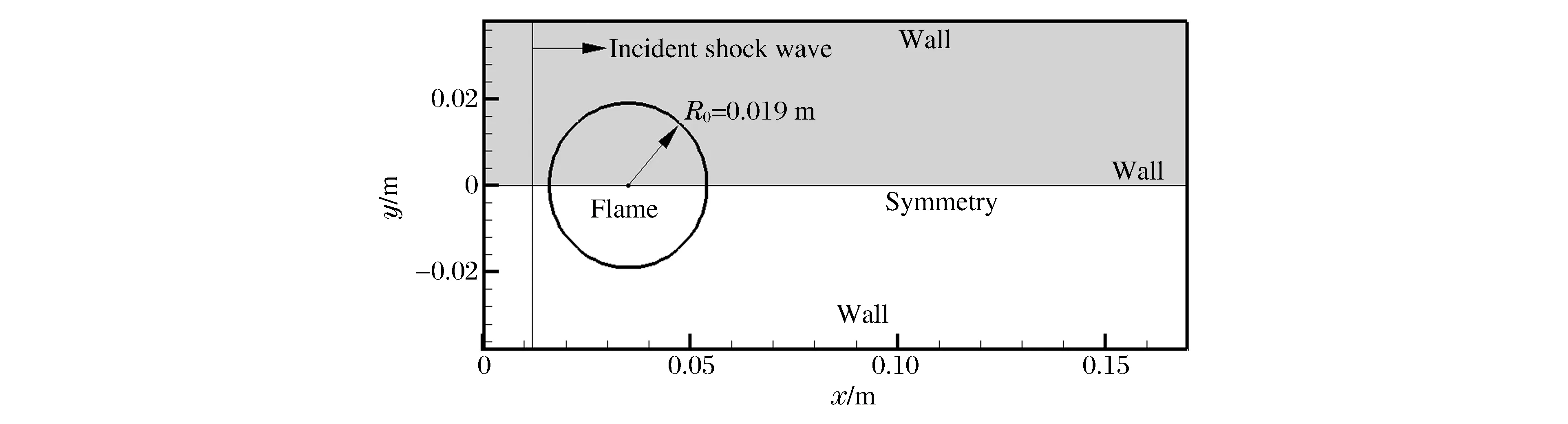
圖1 計算區域和初始流場示意圖Fig.1 Computational domain and initial flow field

1.3 并行計算

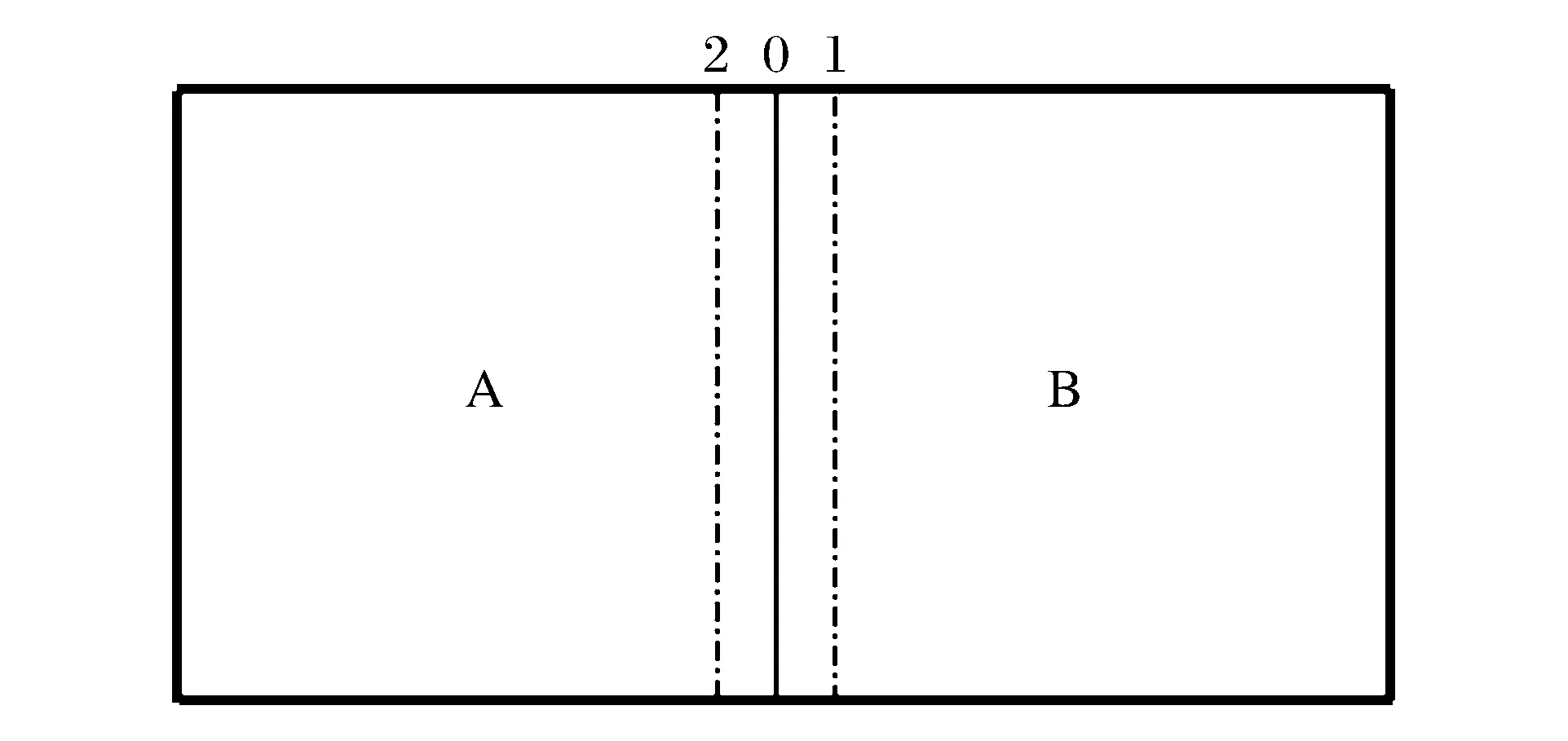
圖2 流場分區示意圖Fig.2 Schematic of flow field block

由于采用較高的網格分辨率，計算規模較大，因此將采用MPI信息傳遞方法對已有程序進行并行化處理，即將計算區域劃分為N個子分區并初始化，當程序開始運行后，系統同時啟動N個進程進行計算。由于本文數值格式在計算網格界面通量時用到界面兩側各一層網格的值，因此在進行每一步的計算之前，需對每個分區的邊界條件進行處理，而邊界條件分為2種:物理邊界和相鄰子分區間的內邊界。對于物理邊界，可根據實際條件直接設置，其中，計算區域上邊界(y=0.038 m)和x方向右端面為管壁，均采用無滑移的剛性絕熱壁面邊界；y=0 m處為對稱面，采用對稱邊界；x方向左端面處采用零梯度邊界；而分區內邊界則需用MPI庫函數對分區間的數據進行傳遞，如圖2所示，邊界0是分區A和B之間的內邊界，邊界1是分區A在分區B內的虛擬邊界，邊界2是分區B在分區A內的虛擬邊界，具體交換方式如下：將分區A內落在邊界2和0之間的這一層網格數據通過MPI庫函數發送給區域B，作為區域B計算邊界通量時需要的值，而將分區B內落在邊界0和1之間的一層網格值發送給區域A，供區域A計算邊界通量，這種方法保證了在分區內邊界處的連續性。

2 結果與討論

2.1 實驗驗證

數值方法和化學模型的可靠性通過計算結果與文獻[5]中實驗的對比來驗證。圖3顯示了激波陣面距火焰點火位置(初始球形火焰中心)的距離、變形火焰寬度和高度三者隨時間的變化，所有結果均采用火焰初始半徑R0進行量綱一處理，通過圖中對比可以看出，激波陣面距點火位置的距離、火焰尺寸的變化均與實驗結果吻合較好，驗證了本文所用計算方法和化學反應各參數的合理性與可靠性。除采用火焰面位置等宏觀量驗證，文獻[13-14]中還對比了不同時刻的火焰結構形態，發現計算結果與實驗結果一致，表明本文計算的可靠性。

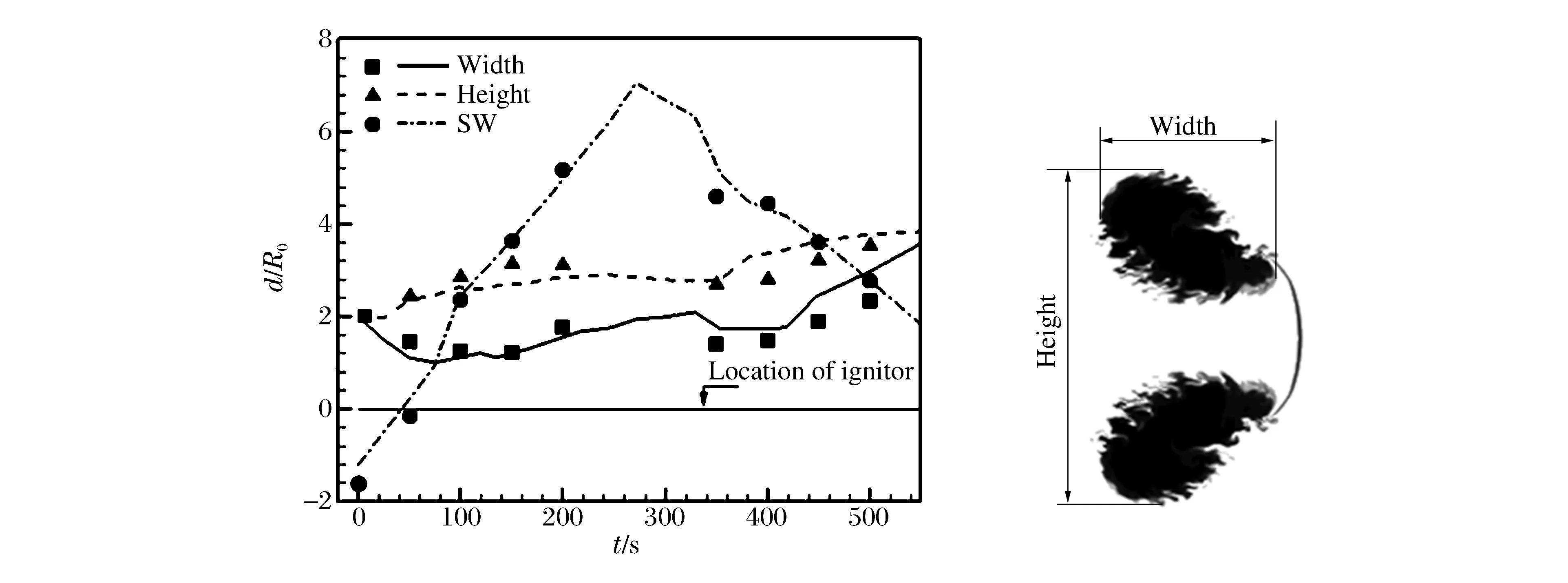
圖3 激波距點火位置距離、火焰界面寬度和高度計算結果(曲線)與實驗結果(符號)[5]的對比Fig.3 Comparisons between calculated (curves) and experimental results (symbols) [5]about distance between shock wave and ignitor, height and width of deformed flame

2.2 渦量演化過程

為了考察激波沖擊火焰過程中的渦量演化過程，圖4首先給出了各時刻火焰區渦量ω的可視化結果，其中圖4(a)～(d)為入射激波波后情形，圖4(e)～(h)為反射激波波后情形。從圖中可以看出，渦量首先出現在火焰界面上，但隨著火焰的旋轉變形，界面處的渦量逐漸向火焰中心集中，同時在黏性作用下發生衰減；當反射激波與火焰發生二次作用后，火焰內部渦量得到強化，形成紅色與藍色2個旋轉方向相反的主渦量，從而誘導火焰結構向壁面發生翻轉，同時火焰邊界的小尺度渦量也得到極大增強，進而導致火焰界面皺褶增強。

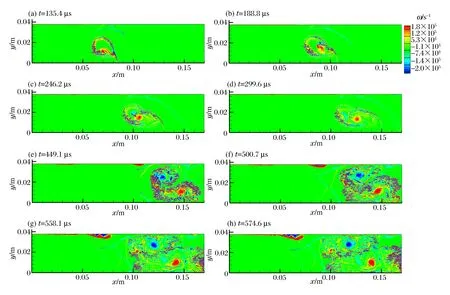
圖4 火焰區渦量變化Fig.4 Vorticity variation of the flame zone

2.3 渦動力學分析

為澄清火焰區域內渦量隨時間演變的內在機制，給出二維理想流體的渦量動力學方程：

(5)

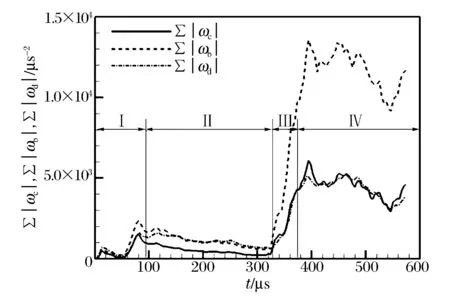
圖5 火焰區內各輸運項絕對值之和隨時間的變化Fig.5 Time histories of the sum of absolute values for per transport term within flame region

式中：D/Dt=?/?t+·u，等號右側第1項為壓縮項ωc，第2項為斜壓項ωb，第3項為耗散項ωd。圖5給出了火焰區域內渦量空間上的各輸運項絕對值之和隨時間的變化過程，分別記為|ωc|、|ωb|和|ωd|，值越大表示該輸運項對渦量變化的影響越大，圖中曲線的變化過程可分為4個階段：Ⅰ為入射激波壓縮階段(0～94 μs)，Ⅱ為火焰膨脹階段(94～328 μs)，Ⅲ為反射激波壓縮階段(328～374μs)，Ⅳ為火焰二次膨脹階段。從圖中可以看出，斜壓效應一直是火焰區域內渦量變化的主要原因，特別是在Ⅲ和Ⅳ階段，反射激波與變形火焰二次作用可引發更強的斜壓效應，這表明圖4(e)～(h)中渦量變化主要受斜壓效應影響。需要注意的是，Ⅳ階段中壓縮項和耗散項變化趨勢基本一致，但兩者的變化原因并不相同：入射激波在流向右端固壁面反射后，激波強度增強，對變形火焰的壓縮作用更強，因而引起火焰區內壓縮項的大幅提升，此時，反射波后的溫度壓力進一步升高，氣體黏性會隨之增大，因此耗散項在反射波后也得到了較大增強。

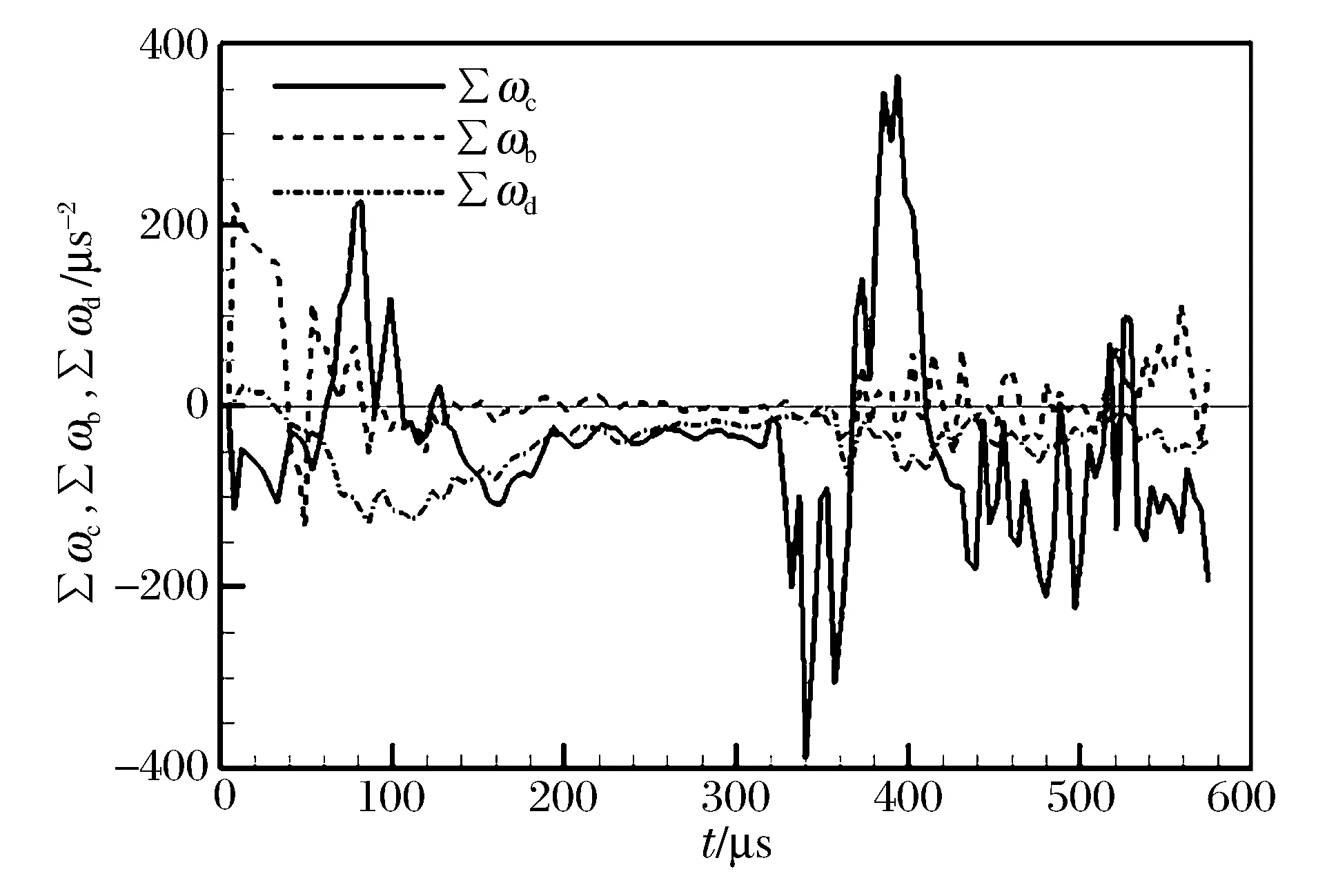
圖6 火焰區內各輸運項正負值之和隨時間的變化Fig.6 Time histories of the sum of positive and negative values for per transport term within flame zone

式(5)中各輸運項在火焰區域內不同位置具有不同的正負值，除通過圖5中各輸運項絕對值之和來分析輸運項對渦量生成的影響之外，還可利用各輸運項正負值之和表征輸運項對渦量生成所起的作用，分別記為ωc、ωb和ωd，即輸運項正負值之和大于零時促進渦量生成，反之則抑制渦量生成，所得曲線見圖6。結果表明，斜壓項始終基本起促進渦量形成的作用，而壓縮項、耗散項在火焰膨脹時(參見圖5中Ⅱ和Ⅳ階段)對渦量生成主要起抑制作用，因此，渦量強度在火焰膨脹期內降低主要受火焰快速膨脹的影響，尤其在反射波后(Ⅳ階段)，火焰劇烈膨脹，并且氣體黏性進一步增強，從而能夠引發火焰區渦量強度快速下降，這與文獻[14]中得到的渦量強度變化規律一致。

圖5～6結果表明，由密度梯度和壓力梯度方向不一致所引起的斜壓項是促進火焰區內渦量生成的關鍵因素。為定量比較反射激波前后斜壓項的變化，圖7定量給出了入射及反射激波波后特定時刻火焰內斜壓項最大值ωb,max和最小值ωb,min的變化。圖中結果表明，反射激波波后(圖5中Ⅳ階段)斜壓項的強度比入射激波波后(圖5中Ⅱ階段)斜壓項強度強；入射激波波后斜壓項的強度在緩慢降低；而反射激波波后，斜壓項強度在火焰區劇烈的燃燒膨脹和增大的耗散作用下降低幅度較大，但從t=500.7s(圖4(f)對應時刻)開始，變形火焰與右端固壁發生碰撞，使得斜壓項強度得到一定程度的增強，隨后斜壓項強度受火焰膨脹和黏性的影響繼續降低。

2.4 環量分析

渦量的強度可以通過環量來表達。為進一步研究火焰區渦量特性，考察火焰區內環量隨時間的變化過程(見圖8)，其中+和-分別代表火焰區正負環量的絕對值，而為正負環量之和，即火焰區的凈環量。本文計算環量采用公式如下：

(6)

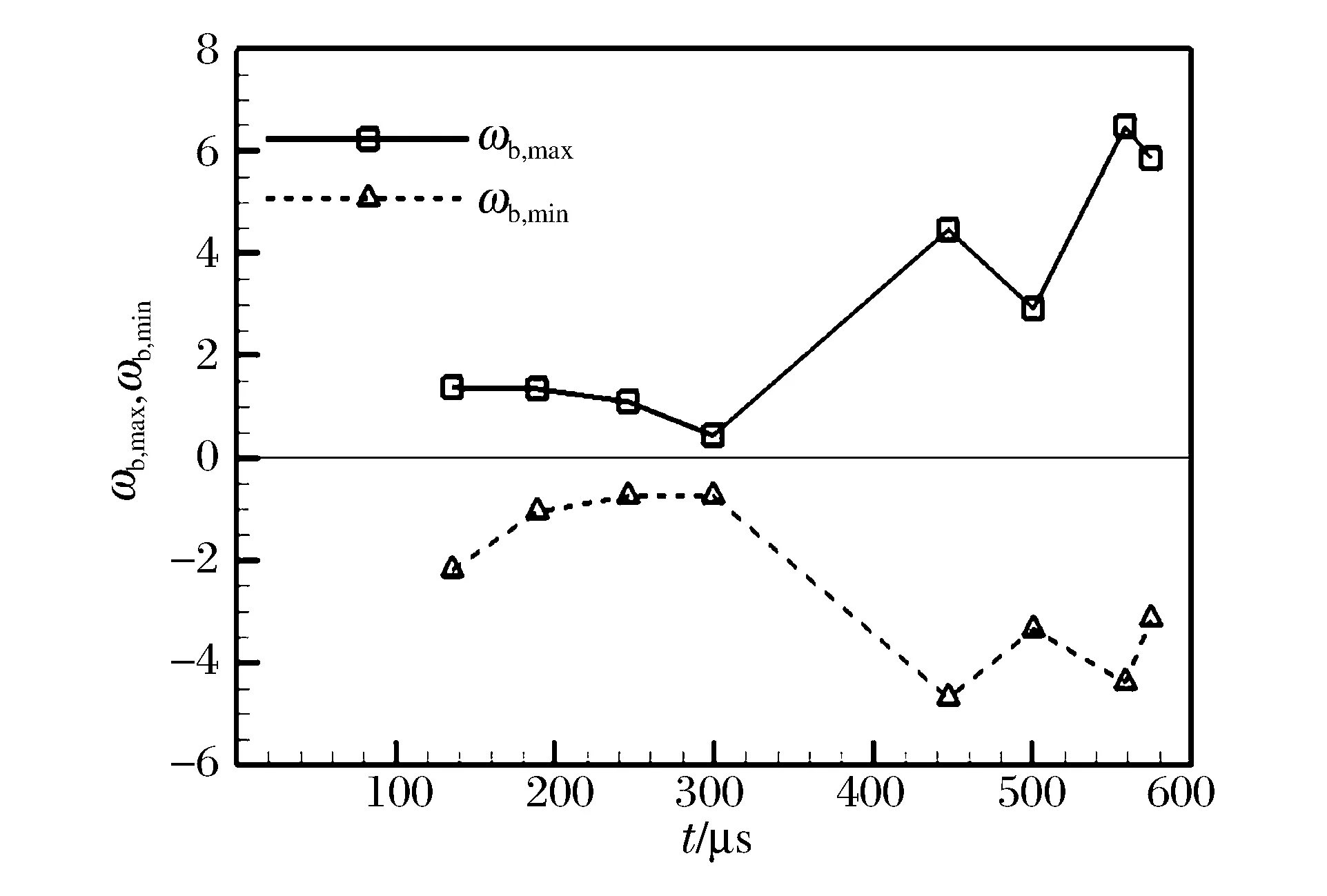
圖7 火焰區內斜壓項最大值和最小值隨時間的變化Fig.7 Time histories of max and min values of baroclinic term within flame zone

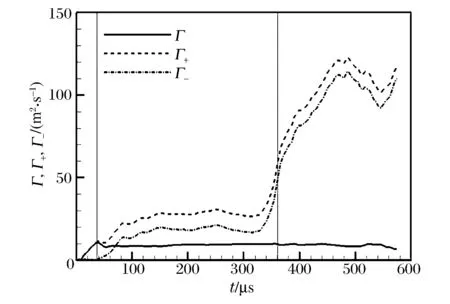
圖8 火焰區內環量隨時間的變化Fig.8 Time histories of circulationwithin flame zone

式中：下標F代表火焰區域(定義為反應物質量分數Y≤0.99)，為渦量。從圖8中可以看出，正負環量在入射及反射激波與火焰作用時(分別對應圖5中Ⅰ和Ⅲ階段)均快速上升，在入射激波及反射激波波后變化幅度放緩。由式(6)可知，環量變化同時受火焰面積和渦量兩者變化的影響，而文獻[15]表明火焰面積在Ⅰ和Ⅲ階段內減小，在Ⅱ和Ⅳ階段內增加，特別是Ⅳ階段內增加速度較快，因此結合圖8可知，火焰區內渦量強度在Ⅰ、Ⅲ階段內上升，在Ⅱ和Ⅳ階段內下降，尤其在Ⅳ階段內下降幅度較大，這與2.3節及文獻[14]中的結論一致。

此外，本文中還將上述環量計算結果與激波與惰性氣泡作用下的環量模型(PB模型[17]和YKZ模型[18])的計算結果進行了對比。PB和YKZ模型選取激波剛掃過氣泡下游極點的時刻，在簡化的假設前提下，對半圓型氣泡區域內的渦量進行積分。圖8中垂直實線分別對應t=36.94、361.2 μs，即入射和反射激波剛好掃過火焰區域的時刻，與PB和YKZ模型計算結果的對比見表1。結果表明，YKZ模型預測結果與本文計算結果吻合較好，而PB模型計算的環量值大致為數值計算結果的2倍，這與G.Layes等[19]的結論一致。傳統的PB和YKZ模型均用于入射激波與惰性氣泡相互作用的過程，而本文中研究發現YKZ模型還適用于入射及反射激波掃過火焰后的環量預測，這實際上表明在激波壓縮火焰階段(對應圖5中I和III階段)，火焰區的變化主要受物理過程而非化學反應過程控制。

表1 火焰區域內的環量計算結果

3 結 論

基于二維帶化學反應的NS方程，對平面入射激波及其反射激波沖擊球形火焰的現象進行了數值研究，采用并行計算克服高精度時空分辨率帶來的計算量過大問題，主要從渦量可視化、渦動力學及環量的角度分析火焰區內的渦量特性。計算結果表明，火焰區內渦量在激波壓縮階段快速增長，在火焰膨脹階段下降；斜壓項在火焰區內渦量變化過程中起主導作用，主要促進渦量生成，而壓縮項和耗散項在火焰燃燒膨脹階段均抑制渦量生成；此外，環量計算還表明在激波壓縮階段，火焰區變化主要受物理過程控制。

[1] Lindl J D, McCrory R L, Campbell E M. Progress toward ignition and burn propagation in inertial confinement fusion[J]. Physics Today, 1992,45(9):32-40.

[2] Marble F E, Hendrick G J, Zukoski E E. Progress toward shock enhancement of supersonic combustion process[R]. AIAA, 1987:87-1880.

[3] Oran E S, Gamezo V N. Origins of the deflagration-to-detonation transition in gas-phrase combustion[J]. Combustion and Flame, 2007,148(1/2):4-47.

[4] Markstein G H. A shock-tube study of flame front-pressure wave interaction[C]∥6th Symposium (International) on Combustion. Pittsburgh, USA: The Combustion Institute, 1957:387-398.

[5] Thomas G O, Bambrey R, Brown C. Experimental observations of flame acceleration and transition to detonation following shock-flame interaction[J]. Combustion Theory and Modeling, 2001,5(4):573-594.

[6] Batley G A, Mcintosh A C, Brindley J, et al. A numerical study of the vorticity field generated by the baroclinic effect due to the propagation of a planar pressure wave through a cylindrical premixed laminar flame[J]. Journal of Fluid Mechanics, 1994,279:217-237.

[7] Batley G A, Mcintosh A C, Brindley J. The baroclinic effect in combustion[J]. Mathematical and Computer Modelling, 1996,24(8):165-176.

[8] Ju Y, Shimano A, Inoue O. Vorticity generation and flame distortion induced by shock flame interaction[C]∥27th Symposium (International) on Combustion. Pittsburgh, USA: The Combustion Institute, 1998:735-741.

[9] Khokhlov A M, Oran E S, Chtchelkanova A Y, et al. Interaction of a shock with a sinusoidally perturbed flame[J]. Combustion and Flame, 1999,117(1/2): 99-116.

[10] Khokhlov A M, Oran E S, Thomas G O. Numerical simulation of deflagration-to-detonation transition: The role of shock-flame interactions in turbulent flame[J]. Combustion and Flame, 1999,117(3):323-339.

[11] Khokhlov A M, Oran E S. Numerical simulation of detonation initiation in a flame brush: The role of hot spots[J]. Combustion and Flame, 1999,119(4):400-416.

[12] Dong G, Fan B C, Ye J F. Numerical investigation of ethylene flame bubble instability induced by shock waves[J]. Shock Waves, 2008,17(6):409-419.

[13] 朱躍進，董剛，范寶春.受限空間內激波與火焰作用的三維計算[J].推進技術,2012,33(3):405-411. Zhu Yue-jin, Dong Gang, Fan Bao-chun. Three-dimensional computation of the interactions between shock waves and flame in a confined space[J]. Journal of Propulsion Technology, 2012,33(3):405-411.

[14] Zhu Y J, Dong G, Liu Y X. Three-dimensional numerical simulations of spherical flame evolutions in shock and reshock accelerated flows[J]. Combustion Science and Technology, 2013,185(10):1415-1440.

[15] 朱躍進，董剛，劉怡昕，等.激波誘導火焰變形、混合和燃燒的數值研究[J].爆炸與沖擊,2013,33(4):430-437. Zhu Yue-jin, Dong Gang, Liu Yi-xin, et al. A numerical study on shock induced distortion, mixing and combustion of flame[J]. Explosion and Shock Waves, 2013,33(4):430-437.

[16] 都志輝.高性能計算之并行編程技術----MPI并行程序設計[M].北京:清華大學出版社,2001.

[17] Picone J M, Boris J P. Vorticity generation by shock propagation through bubbles in a gas[J]. Journal of Fluid Mechanics, 1988,189:23-51.

[18] Yang J, Kubota T, Zukoski E E. A model for characterization of a vortex pair formed by shock passage over a light-gas inhomogeneity[J]. Journal of Fluid Mechanics, 1994,258:217-244.

[19] Layes G, Jourdan G, Houas L. Experimental study on a plane shock wave accelerating a gas bubble[J]. Physics of Fluids, 2009,21(7):074102.

(責任編輯 曾月蓉)

A study of vorticity characteristics of shock-flame interaction

Zhu Yue-jin1,2, Dong Gang2

(1.SchoolofEnergyandPowerEngineering,JiangsuUniversity,Zhenjiang212013,Jiangsu,China; 2.KeyLaboratoryofTransientPhysics,NanjingUniversityofScienceandTechnology,Nanjing210094,Jiangsu,China)

The phenomenon of shock wave interacting with a flame involves a series of complicated physical and chemical processes, in which the generation and evolution of vorticity play an important role in controlling flame development. To systematically analyze the vorticity characteristics in the course of shock-flame interaction, a numerical study of a planar incident shock wave and its reflected wave interaction with a spherical flame was carried out by using the two-dimensional Navier-Stokes equations coupled with chemical reaction, and the requirement of high-resolution grid was met via the parallel computation. It is found that the baroclinic term plays a dominant role in the generation of vorticity within the flame zone, and the compression and dissipation terms restrain the generation of vorticity in the flame expanding stages. Besides, in the compression stages, the evolution of flame is mainly affected by the physical-rather than chemical-process.

mechanics of explosion; vorticity; Navier-Stokes equations; flame; shock wave; baroclinic term

10.11883/1001-1455(2015)06-0839-07

2014-04-29；

2014-08-21

國家自然科學基金項目(11372140,11402102);江蘇省自然科學基金青年項目(BK20140524); 江蘇大學高級專業人才科研啟動基金項目(14JDG031);江蘇省博士后基金項目(1402013B)

朱躍進(1986— )，男，博士，講師,zyjwind@163.com。

O382 國標學科代碼： 13035

A