羽絨蓬松度測定結果不確定度的評定

趙金晶 董愛林 陳惠敏

（江蘇省紡織產品質量監督檢驗研究院，江蘇南京 210007）

測量不確定度表征合理地賦予被測量之值的分散性，是與測量結果相聯系的參數[1]。在ISO /IEC 17025《檢測和校準實驗室能力認可準則》[2]中規定，測試報告需有評估測量不確定度的聲明（適用時），如果不確定度與測試結果的有效性或應用有關，或客戶說明中提出要求，或不確定度影響與規范限量的符合性時，測試報告中需加入有關不確定度的信息。測試結果包含不確定度信息后，可使測試結果的表達更科學、完整。另外，測量不確定度在實驗室數據比對、方法確認、標準設備校準、量值溯源以及實驗室質量控制和管理等方面具有重要的意義。

冬季常見防寒保暖的羽絨服，消費者最關注的是保暖功能。蓬松度是指羽毛羽絨的彈性程度[3]，羽絨蓬松度越好，滯留的空氣量越多，保暖性越好。因此，蓬松度是羽絨產品重要的檢驗項目，國家標準對其也做了相應規定，國內對于羽絨蓬松性能相關因素之間關系的研究也正逐步展開。本文通過對羽絨蓬松度測量不確定度的來源進行分析探討，定量表征測量結果的質量，確定羽絨蓬松度測定結果的可信程度。

本文主要按照GB/T 14272-2011開展試驗并進行不確定度評定,同時FZ/T 80001-2002、GB/T 10288-2003等標準[4,5]亦規定了完全相同或相似的羽絨蓬松度的檢測方法，本文的分析方法和結果具備一定的普適性。

1 試驗

1.1 試驗方法及原理

依據GB/T 14272-2011《羽絨服裝》附錄C中蓬松度的測定方法，其原理是通過測量在一定口徑的容器內一定量的羽絨羽毛在恒重的壓力下所占的體積來計算蓬松度。

1.2 試驗樣品

實驗選取含絨量標稱為 80% (x%為樣品的含絨量)的灰鴨絨作為實驗樣品。

1.3 試驗條件及儀器

樣品在恒溫箱（50℃±5℃）內恒溫處理1h后，用手逐把抖入前處理箱內，在溫度20℃±2℃及相對濕度65% ±4%的標準大氣中靜置24h使其疏松，恢復原狀備用。

儀器設備有天平、秒表、前處理箱、蓬松度儀(桶壁兩對面有刻度的有機玻璃圓筒，桶高75cm，內徑為24cm，桶底為有機玻璃活絡底。桶內有直徑為24cm，質量為68.4g的可以在桶內上下自由滑動的圓形鋁質壓板)、恒溫箱。

1.4 試驗步驟

1.4.1 從在前處理箱內已放置24h的羽毛、羽絨樣品中，稱取兩個28.5g試樣，逐把抖入蓬松儀內，再用硬質玻璃棒充分攪拌并鋪平。

1.4.2 鋪平后，將鋁質壓板蓋在羽毛、羽絨上面，在松手放下壓板的同時按下秒表，任壓板緩緩下壓。1 min 后記錄壓板壓在蓬松儀桶壁的兩邊刻度值，取其平均值。同一試樣重復做三次。

1.4.3 結果計算。按式（1）計算三次試驗結果的平均值，作為試樣蓬松度的測定值。計算結果按GB/T 8170[6]修約至小數點后一位。

（1）式中：h1為第一次試驗結果的刻度平均值（cm）；h2為第二次試驗結果的刻度平均值（cm）；h3為第三次試驗結果的刻度平均值（cm）。最終結果取兩個試樣的平均值，計算結果按GB/T 8170修約至小數點后一位。

2 不確定度來源分析和評定

根據羽絨蓬松度測定的程序步驟，分析羽絨蓬松度不確定度的來源的因素，具體關系如圖1所示：

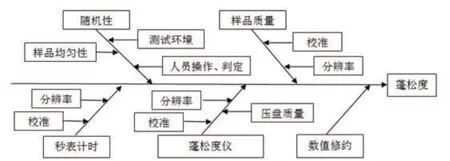
圖1 蓬松度測定不確定來源圖

2.1 隨機效應導致的不確定度

從測試方法可以看出，羽絨蓬松度的測量主要靠人工操作，因此測量不確定度將部分來自于試樣取樣、前處理和實驗進行過程中環境因素（溫度、濕度等）的隨機性和實驗人員操作、判定的隨機性。

按照1.4所述方法，我們將一組相同樣品在不同的實驗時間，由不同的實驗人員分別進行取樣、前處理和實驗測定，得到蓬松度測量數據見表1。

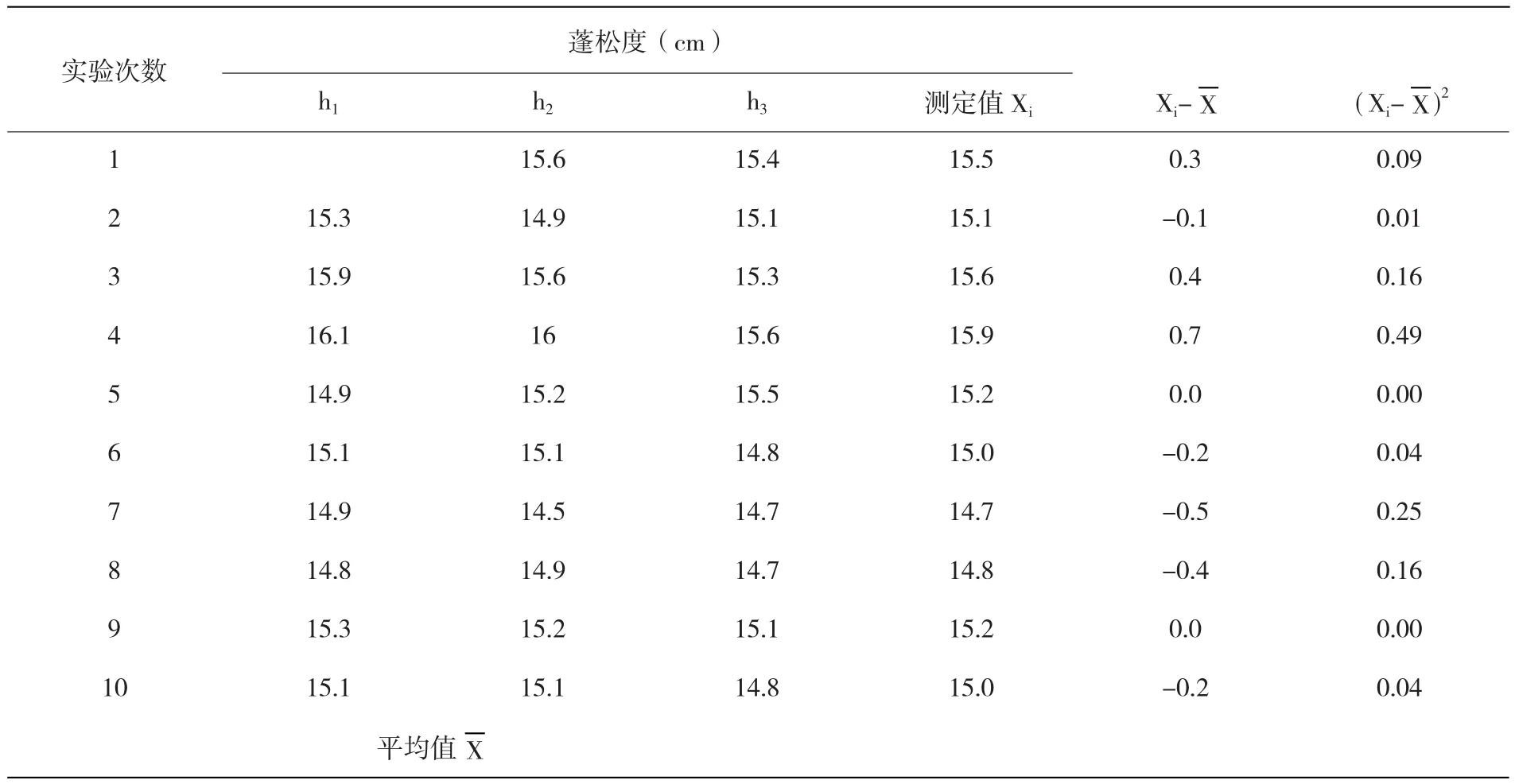
表1 樣品蓬松度測量結果及偏差計算

單次測量的不確定度（試驗標準偏差）由以下貝塞爾公式計算：

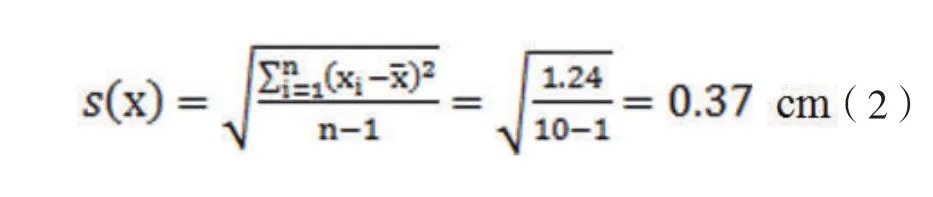
（2）式中Xi為第i次蓬松度的測定值，X為n次測量蓬松度的平均值，n為測量總次數，S(x)為單次測量的不確定度。

采用肖維勒準則剔除異常值,對于測量次數為10次時,異常界限系數k=1.96,則

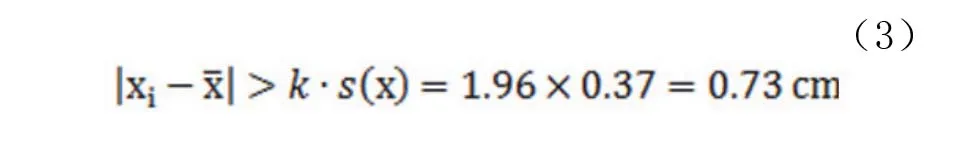
據此檢查表1中10組測量數據，均為有效測量值。

在日常分析中，測定兩份樣品報告平均值，故平均值的標準偏差為：

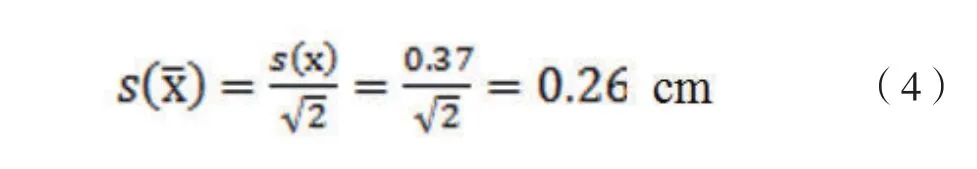
此標準偏差相對于15.2cm的蓬松度而言，測量的隨機效應產生的相對不確定度為

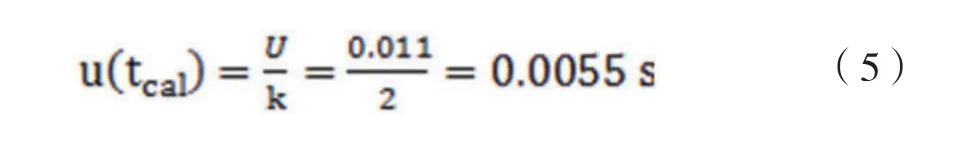
2.2 樣品質量測量引入的不確定度

a. 天平稱量的校準

實驗室所用天平為梅特勒-托利多PL2002型電子天平。由檢定證書可知．天平偏載誤差±0.02g，重復性誤差±0.01g，示值誤差±0．02g (0≤m≤500g)、±0.02g(500＜m≤2000g)、±0.02g (2000＜m≤2100g)，樣品質量約為28.5g，假定分布均勻（矩形分布），則由天平校準引起的不確定度分量可表示為：

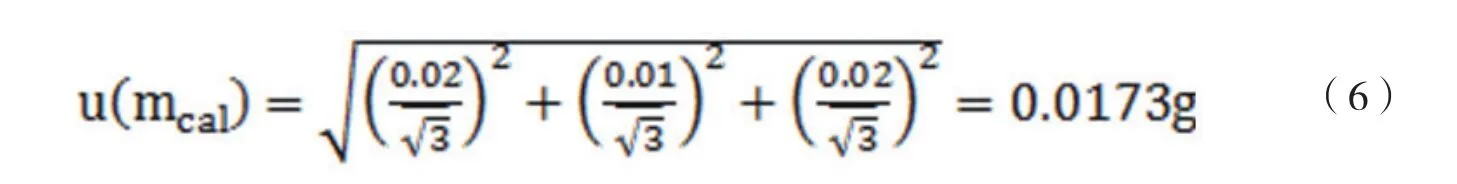
b. 天平稱量的讀數精度(分辨率)

試驗實際使用的天平分度值為0.1g，假設為矩形分布的半寬，則由天平稱量讀數引起的不確定度分量可表示為：

上述2種分量合成得到樣品質量測量的標準不確定度為：

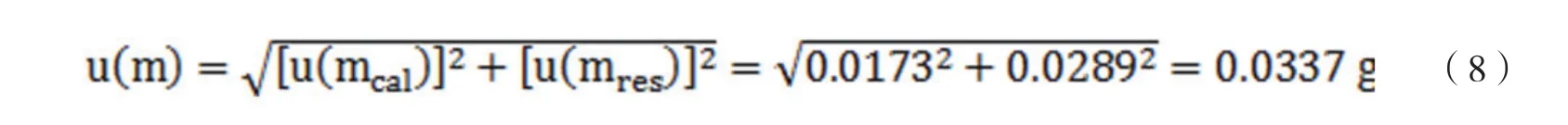
對于28.5g樣品而言，樣品質量測量的相對不確定度為：

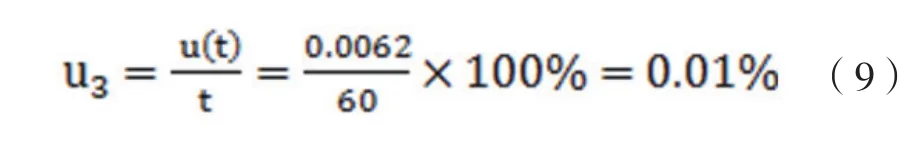
2.3 時間測量引入的不確定度

a. 秒表計時的校準

用于計時的秒表，根據檢定證書標明其在測量范圍1～120s條件下，擴展不確定度U=0.011s，k=2，則其標準不確定度為：

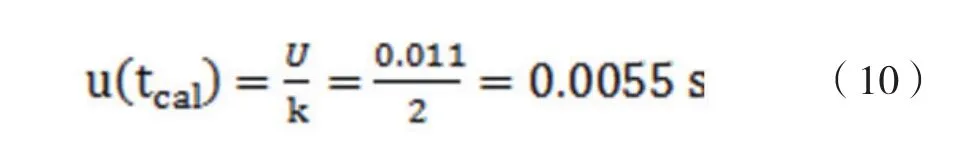
b. 秒表計時的讀數精度(分辨率)

使用的秒表分度值為0.01s，假設為矩形分布的半寬，則有

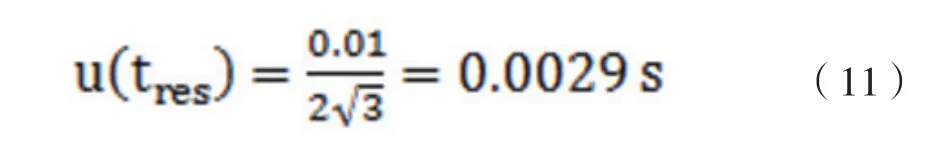
上述2種分量合成得到時間測量的標準不確定度為：

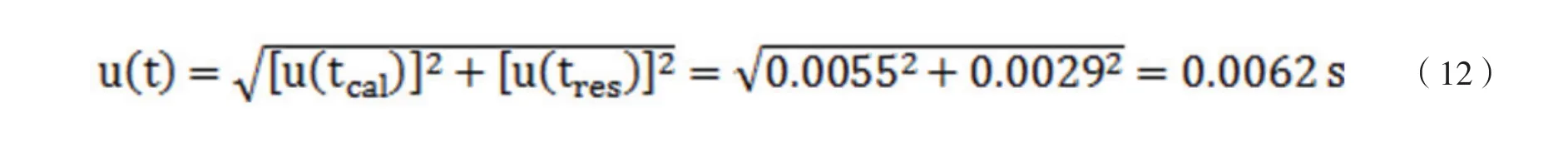
對于60s樣品實驗時間而言，時間測量的相對不確定度為：

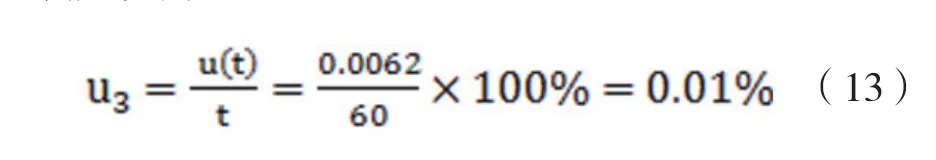
2.4 蓬松度儀引入的不確定度

本實驗所用蓬松度儀存在兩方面主要的不確定因素，一是蓬松度儀體積測量,二是蓬松度儀所用壓盤質量。

2.4.1 蓬松度儀體積測量

a. 蓬松度儀體積的校準

根據計量證書提供的結果，在符合要求的實驗環境下，實驗所用儀器容積為16000±104.2cm3（計量中已考慮容器底面積的變化，故后續不再重復計算底面積變化引起的不確定度）,但并未給出置信水平或分布情況信息,為此假設符合三角形分布,則有：

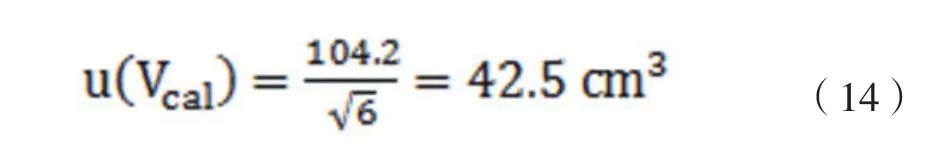
b. 蓬松度儀的讀數精度(分辨率)

實驗所用儀器分度值為 200cm3,假設為矩形分布的半寬,則有：

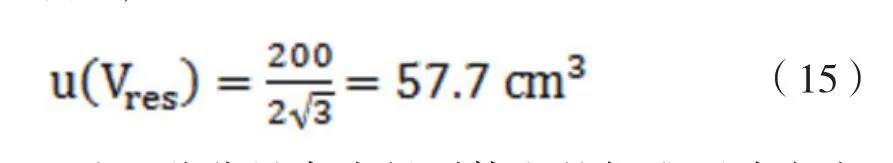
上述2種分量合成得到體積的標準不確定度為：

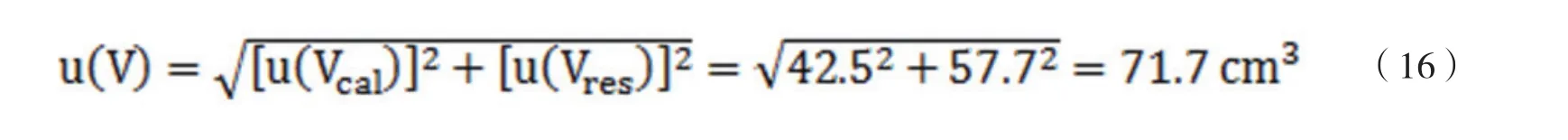
相對于15.2cm的蓬松度（對應體積V=15.2*3.14*122=6872.8 cm3），蓬松度儀測量的相對合成不確定度為：

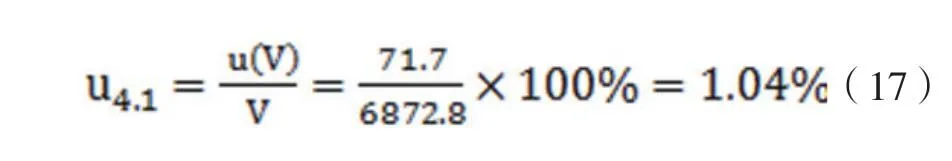
2.4.2 蓬松度儀壓盤質量

根據儀器計量證書提供的結果，壓盤質量為68.4±0.3g，假設為矩形分布，壓盤質量相對不確定度為：

2.5 數值修約引入的不確定度

按照GB/T 14272-2011試驗方法的規定，計算結果修約到0.1cm。根據JJF1059-1999[7]規定，計算平均值修約導致的不確定度：

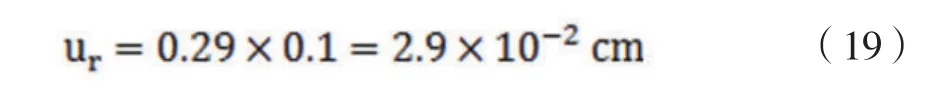
相對于15.2cm的蓬松度，修約導致的相對不確定度為：

2.6 合成不確定度

有上述分析可知，相對合成不確定度的計算為：

合成標準不確定度為：

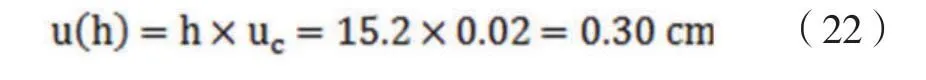
2.7 擴展不確定度

取包含因子k = 2 ( 近似95%置信概率) ，則擴展不確定度為：

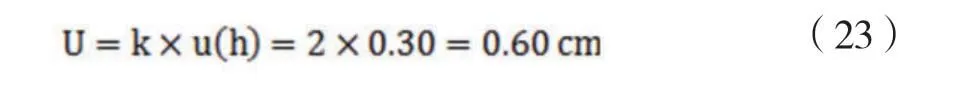
2.8 不確定度報告與表示

綜上,實驗羽絨蓬松度的結果可表示為： k = 2。

3 結論

分析顯示，在本文所采用的試驗方法和測量條件下，各不確定度分量對羽絨的蓬松度的影響不同。總體來說，測量的隨機效應u1和蓬松度儀的精準程度u4對不確定度總量影響最大。其中，隨機效應導致的不確定度占據了最大的部分，這除了與樣品均勻性、測試環境等客觀因素有關之外，也與實驗人員的操作、判定有直接聯系。與此同時，蓬松度儀作為本項實驗所用到的最為重要的儀器，它也是很重要的一個不確定度分量，其精密程度很大程度上制約了羽絨蓬松度測量的準確性。

所以在檢測過程中要嚴格按照操作程序，使用精度高、穩定性好的儀器設備，并在試驗前認真校準，減少人為因素和判定的不當，遵守數值修約的規定，同時注意應用測量技巧也可有效減少羽絨蓬松度測量中的不確定度。

[1] ISO/lEC Guide 99： 2007 International vocabulary of basic and general terms in metrology (VIM) [s].

[2] ISO/IEC 17025 ： 2005.檢測和校準實驗室能力認可準則[s]．

[3] GB/T 14272-2011.羽絨服裝[s]．

[4] FZ/T 80001-2002.水洗羽毛羽絨試驗方法[s]．

[5] GB/T 10288-2003.羽絨羽毛檢驗方法[s]．

[6] GB/T8170-2008 數值修約規則與極限數值的表示和判定[s]．

[7] JJF 1059-1999. 測量不確定度的評定與表示[s]．