針對特征模型的辨識方法對比研究及其應用
田雙文
(南京理工大學,江蘇 南京210094)
0 引言
建模的目的是為了分析和設計系統,特征模型的提出可以不依賴被控對象的精確數學模型,而將對象動力學特征、環境特征和控制性能要求相結合進行建模,其特點是對象特征模型和實際對象在輸出上是等價的,在穩態情況下,輸出是相等的[1]。特征模型建立的形式比原來對象的動力學方程簡單,易于控制器設計,工程實現容易,它把高階模型有關信息都壓縮到幾個特征參量之中,同時又不丟失信息[2]。
吳宏鑫院士提出的黃金分割控制能保證參數未知的系統在過渡過程階段,參數設計未收斂情況下閉環系統穩定[3],雖然黃金分割控制設計簡單、調試方便,但其本身主要依賴于被控對象特征模型的在線參數辨識值,因此,在對系統特征模型進行參數辨識時所選擇的辨識算法對特征模型的建模精度及其最終控制器控制效果有很大的影響。
目前國內常采用以遞推最小二乘法(以下簡稱RLS算法)為主的全量參數估計,這種方法能使辨識參數快速收斂到真值,這種方法的不足之處在于需要計算P(k)陣,計算量較大,而且P(k)陣中遺忘因子λ選取較麻煩,當λ=1時,隨著運行時間的增加,P(k)趨于0,使參數估計失去能力;當λ<1時,隨著k的增加,P(k)趨于無窮,造成參數估計大幅波動甚至發散,另外對于敏感參數β0的辨識值過小且收斂速度慢,這將導致不利于控制器設計[4]。
另一種方法是采用帶遺忘因子的隨機梯度下降法(以下簡稱FSG 算法),這種方法無需計算P(k)陣,且不會導致參數估計發散或者失去估計能力,敏感參數g0(k)的辨識值收斂速度快,同時參數估計收斂值隨初值選擇不同而不同,無唯一解,這樣可以選擇合適的g0(k)來進行控制器設計[5]。
本文采用最小二乘法和梯度下降法兩種方法分別對特征模型參數進行辨識,重點介紹梯度下降法的參數選取問題與辨識效果,最后對變慣量伺服系統進行在線參數辨識并采用黃金分割控制器進行自適應控制,仿真結果表明,采用梯度下降法能夠有效地對不同慣量情況下系統特征參數g0(k)進行辨識,有利于控制器設計,而最小二乘法所辨識的g0(k)不利于控制器設計。
1 特征模型理論簡介
記非線性系統為:
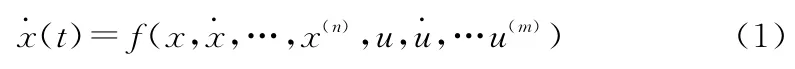
如果被控對象能用系統(1)表示,且滿足上面(1)~(4)的假設,在滿足一定采樣周期ΔT 的條件下,其特征模型可以用一個二階時變差分方程形式來描述:
x(k+1)=f1(k)x(k)+f2(k)x(k-1)+g0(k)u(k)+g1(k)u(k-1)
其中,f1(k)、f2(k)、g0(k)、g1(k)為特征模型的待定參數,需要對其進行實時在線辨識。由于電機模型帶有積分環節,所以其特征模型可簡化為[6]:
x(k+1)=f1(k)x(k)+f2(k)x(k-1)+g0(k)u(k)
式中,f1(k)→2;f2(k)→-1。
2 遞推最小二乘法與帶遺忘因子的隨機梯度下降法簡介
針對永磁同步電機特征模型參數辨識結構如圖1所示,永磁同步電機采用電流環和速度環雙閉環的控制,為研究辨識算法的建模精度問題,輸入信號u(k)為轉速給定信號,輸出信號y(k)為測量的位置信號。
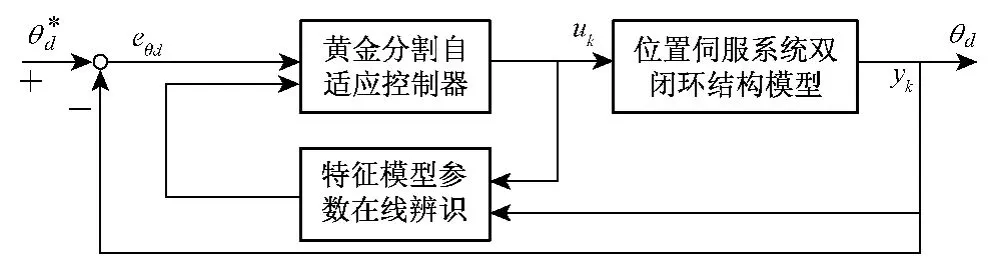
圖1 位置伺服系統控制器結構
RLS算法[5]:
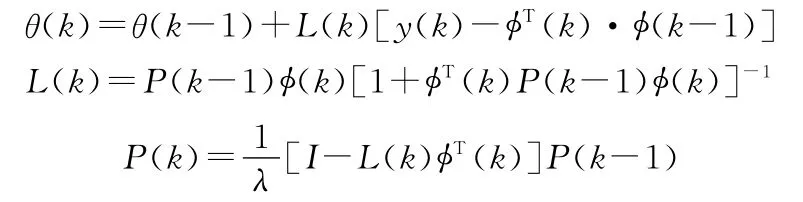
FSG 算法[5]:
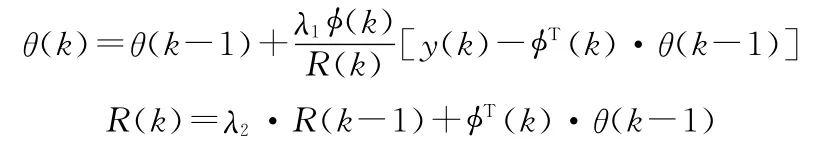
3 辨識對比
不同永磁同步電機參數,采樣周期為0.005s,電機調速采用PI調節,輸入轉速為3 000r/min,初值θ(0)=[1.99-0.99 0.000 1],為使FSG 算法能夠較好地對特征參數進行辨識,需要對輸入信號進行一定的比例縮小,因此取輸入信號放大倍數K=1×10-5,仿真時間為10s。
采用RLS算法和FSG 算法,特征建模誤差e無太大區別,差別在于待辨識值f1(k)、f2(k)、g0(k)這三個參數的辨識效果。在初始階段,采用RLS算法f1(k)、f2(k)兩個參數的變化范圍大,而采用FSG 算法辨識出的f1(k)、f2(k)變化范圍小;對于敏感參數g0(k)的辨識,采用FSG 算法辨識的g0(k)收斂速度要快于RLS算法,而且FSG 算法辨識的g0(k)穩態終值要大于RLS算法辨識的g0(k)。FSG 算法參數估計收斂值與初始參數選擇和輸入信號放大倍數K 有關,選擇不同的初始參數對于g0(k)的終值有不同的辨識效果,選擇不同放大倍數K 會影響g0(k)的數量級別,這樣的好處是可以人為改變g0(k)的辨識值,這對于采用黃金分割控制器會有很好的控制效果,不會像最小二乘法那樣因為g0(k)辨識值很小而導致黃金分割控制性能下降。
4 控制器設計與仿真驗證
黃金分割控制器就是把黃金分割比(l1/l2=0.382/0.618)引入控制器設計中。被控對象二階差分方程為:
y(k)=α1y(k-1)+α2y(k-2)+β0u(k-1)
對象系數α1、α2、β0未知,且在DS之內。
控制器為:


5 結語
針對永磁同步電機特征模型的參數辨識,帶遺忘因子的梯度下降法對于階躍信號和斜坡信號的g0(k)的辨識值有很好的效果,最終控制效果不錯,但對于正弦信號的辨識效果不是很好。由于正弦信號的連續變化,需要重新選取g0(k)的初值與比例因子,以達到辨識值連續變化的目的,最終使得控制器有自適應的效果。
[1]吳宏鑫,胡軍,解永春.基于特征模型的智能自適應控制[M].北京:中國科學技術出版社,2009:47-50.
[2]Uenaka Y,Sazawa M,Ohishi K.Self-tuning Control of both Current Sensor Offset and Electrical Parameter Variations for PM Motor[C]//2010 11th IEEE International Workshop on Advanced Motion Control,2010:649-654.
[3]吳宏鑫,解永春,李智斌.基于特征模型描述的黃金分割智能控制[C]//1996 年中國智能自動化學術會議論文集(上冊),1996.
[4]Ding F,Shi Y,Chen T.Auxiliary Model Based Least-squares Identification Methods for Hammerstein Output-error Systems[J].Systems &Control Letters,2007,56(5):373-380.
[5]李鵬波,胡德文.系統辨識基礎[M].北京:中國水利水電出版社,2006.
[6]孟斌,吳宏鑫.線性定常系統特征模型的證明[J].中國科學:E輯,2007,37(10):1258-1271.

