一種基于MTD中間濾波器噪聲統計的噪聲電平恒虛警方法研究
屈紅剛 張 強 高青松 黃金杰
(西安電子工程研究所 西安 710100)
0 引言
噪聲是限制接收機靈敏度的主要因素。而噪聲的來源是多方面的:從接收機內部來說,電路中的電阻、放大器、混頻器等都會產生噪聲;從接收機外部來說,通過天線引入的天線熱噪聲、天電干擾、宇宙干擾等[1]。一般情況下,接收機的噪聲多用高斯分布表示其統計特性,它是一種鐘形對稱的分布曲線。具有高斯分布的寬帶白噪聲經過窄帶濾波器后的統計分布通常呈現為瑞利分布。在雷達系統中,經超外差接收機中頻放大器后輸出的窄帶噪聲包絡也為瑞利分布,在實際工作中,各種噪聲會使原本采用固定噪聲門限的雷達系統虛警增加,為了使雷達在復雜環境下具有相對穩定的虛警率,本文依據噪聲電平統計特性,采用通過統計MTD 中間濾波器噪聲的方法,實現噪聲電平恒虛警,并將該方法運用于工程應用,驗證了其有效性。
1 噪聲電平恒虛警處理原理
在不考慮雜波情況下,雷達系統的虛警主要是由系統噪聲引起。高斯噪聲通過窄帶線性系統后,其輸出包絡的概率密度函數服從瑞利分布:

式中,σ 為檢波前高斯噪聲的均方值(噪聲電壓的有效值)。
根據瑞利分布可計算出超過門限VT的虛警概率,即


式中,Vo=VT/σ 為相對門限電壓。
由式(2)可得,當門限VT=σ 時,虛警概率Pfa為6.1 × 10-1;當VT= 5σ 時,虛警概率為3.7 ×10-6。可見,在不考慮雜波時,噪聲恒虛警門限等于5 倍噪聲統計均值時,便可使噪聲虛警概率保持在10-6的量級上。
對于瑞利分布來說,不妨引入新變量y=x/ σ,y 的概率密度函數為

式(3)表明,變量y的概率分布與噪聲強度無關,如能將變量x 歸一化為變量y[2],則噪聲強度變化時將保持輸出恒虛警。因此,必須設法檢測出噪聲x的統計平均值,通過相應的電路完成x和σ 相除,便能達到歸一化的結果。
瑞利分布噪聲的平均值,正比于檢波前高斯噪聲的均方差,其統計平均值為
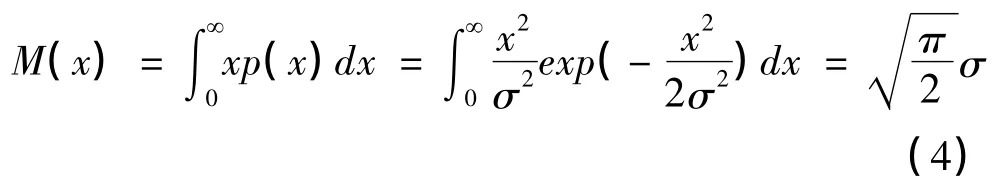
由式(4)可知,噪聲均值M(x)與方差σ 是線性關系。要使虛警概率Pfa保持不變,則Vo要求保持不變,而Vo=VT/σ,因此,只要VT=σ ×K便可保持虛警概率不變,也就是只要VT=M(x)×K'即可保持虛警概率保持不變,只要實時得到噪聲電平值即可實現噪聲電平恒虛警。
2 基于MTD 中間濾波器噪聲統計的噪聲電平恒虛警原理
對于相參積累的脈沖多譜勒雷達系統來講,雜波一般由于其速度比較小或者為零[4],其多譜勒頻率遠離MTD 中間濾波器,因此,在無目標時,中間濾波器的輸出可以認為就是噪聲。雖然偶爾有目標可能落入中間濾波器,但是目標數相對于中間濾波器的數目而言是非常小的,例如,某雷達有1344 個波束,每個波束有大約1500 個距離單元,而每個距離單元中間濾波器數目若取2 個,則雷達掃描一幀中間濾波器的樣本數為4032000,而目標在雷達掃描一幀只能出現一次,即使有目標落入中間濾波器,這也不會對噪聲電平的統計構成影響。因此,只要實時統計MTD中間濾波器的輸出結果,就可以得到系統的噪聲電平的均值,噪聲電平均值乘以一個合適的系數即為噪聲電平恒虛警的檢測門限。按照上面的分析,這樣的檢測門限實際上是隨著噪聲的變化而變化,因此,該基于MTD 中間濾波器噪聲統計的噪聲電平恒虛警處理是可以保持系統噪聲虛警概率的恒定。
由于噪聲電平本身是起伏的,在對噪聲電平進行統計時,若統計時間比較短,則統計的噪聲電平起伏也比較大,這將會導致雷達噪聲虛警率產生比較大的變化[5]。一般情況下可選擇一個合適的統計時間段,然后對每一段統計的噪聲電平值按照單回路反饋積累的方法對其進行平均估計。該噪聲電平恒虛警處理原理框圖見圖1。

圖1 基于MTD 中間濾波器噪聲統計的噪聲電平恒虛警原理框圖
噪聲平均值估值[6]按照下式計算:
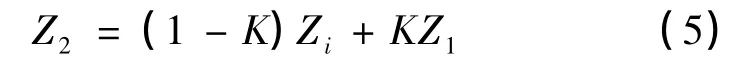
式中,Z1為存儲器中原存儲的噪聲幅度統計平均值,Zi為雷達新的一次采樣得到的噪聲幅度統計平均值,Z2為更新后雷達新的噪聲幅度統計平均值,K 為小于1 的正數。
一般來說,K 越大,前面輸入的作用時間就越長,Z2更新較慢,K 越小,新的噪聲電平統計值起作用越快,Z2更新速度較快。為使Z2快速收斂,Z1起始值可用第一次統計平均值。
3 基于MTD 中間濾波器噪聲統計的噪聲電平恒虛警工程應用
實際工程應用中,某雷達采用16 點相參MTD及-58dB 的切比雪夫加窗處理[7],濾波器組幅頻特性見圖2。
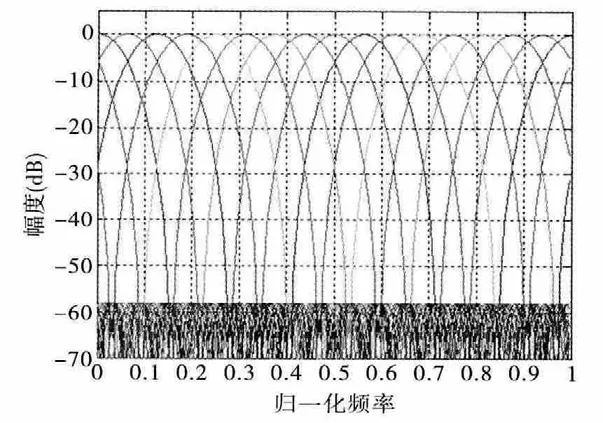
圖2 某雷達MTD 濾波器組特性
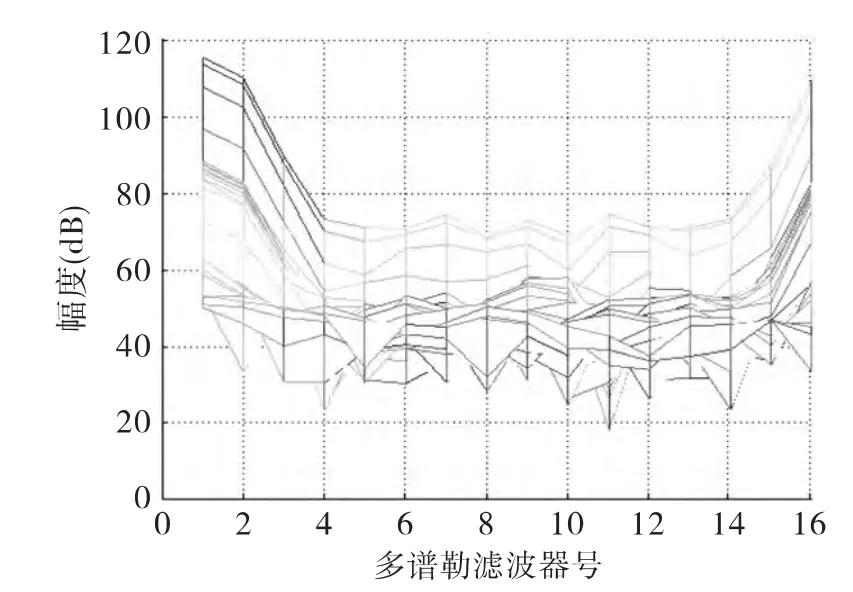
圖3 地物經MTD 處理結果
前面已經分析過,雜波一般主要集中在0 多譜勒濾波器附近,對于某雷達來說,根據脈沖重復頻率以及脈沖積累點數來分析,雜波最多展寬到2#和15#濾波器。為此,我們專門采集了一些數據并對其進行了處理,處理結果見圖3。該圖是地物經過-58dB 切比雪夫加窗后MTD 處理結果,地物目標在0#濾波器幅度為115dB,1#濾波器幅度為109dB,2#濾波器幅度為87dB,14#濾波器幅度為85dB,15#濾波器幅度為107 dB,其他濾波器均小于74dB,也就是說地雜波譜只分布在0#、1#、2#、15#、14#濾波器,沒有延伸到3#~13#濾波器。因此,該雷達選取中間8#和9#兩個濾波器輸出作為噪聲電平統計值。
該雷達搜索波束采用了三種脈沖重復頻率,每個波束平均距離單元數約為1500 個,每個距離單元選中間的2 個濾波器輸出作為噪聲電平統計樣本,噪聲電平每幀(1344 個波束)求一次平均,噪聲電平每次統計平均樣本量多達4032000 個,噪聲電平(歸一化后)最大值不超過100,因此,用一個32 位寄存器用于每個噪聲電平樣本的累加即可滿足需要。
該雷達按照圖4 的處理流程,對于式(5)所定義的平滑估計模型,系數K 為取7/8;噪聲門限系數取5。
下面,我們首先驗證一下前面中間濾波器出現目標時對噪聲電平統計結果的影響情況。即在沒有目標和雜波環境(發射機不開機)下信號處理器實時統計平均噪聲電平值,再利用雷達目標模擬器[8]在某個波束的單個距離單元產生一個動目標,其多普勒速度落入8#濾波器,并將每次噪聲電平平均值記錄下來,結果見表1、2。
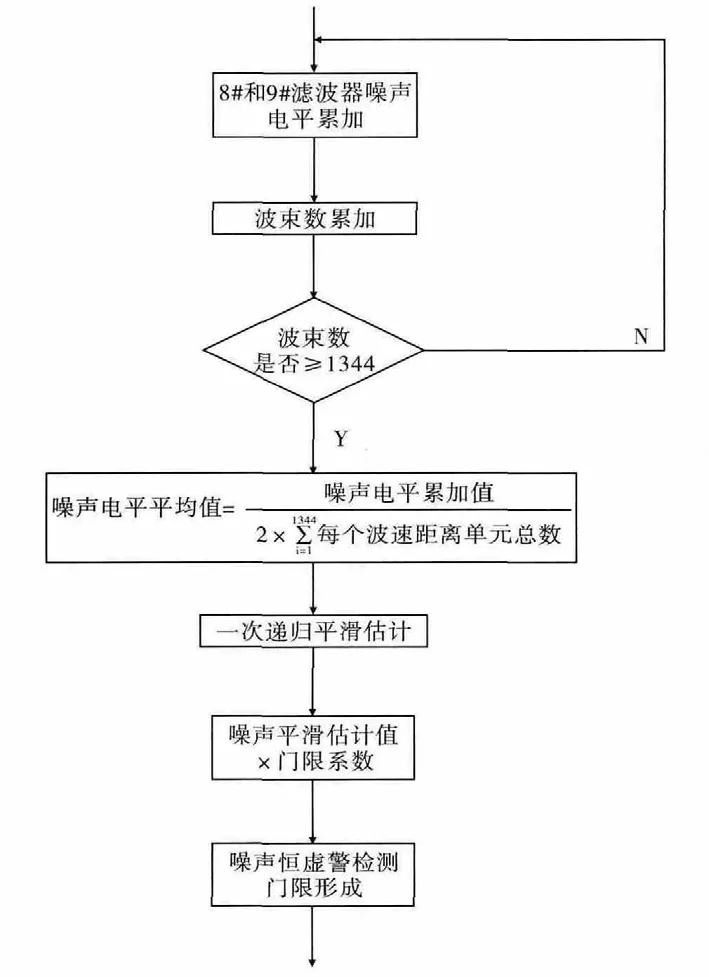
圖4 基于MTD 中間濾波器噪聲統計的噪聲電平恒虛警流程圖

表1 沒有目標和雜波環境下噪聲電平統計結果

表2 有一個目標時噪聲電平值統計結果
表1,表2 中的統計次數指的是雷達完成整個空域掃描的次數,噪聲電平幅度為噪聲經過信號處理器處理后實際輸出的量化幅度。從以上兩組數據來看,中間濾波器偶爾出現目標并不對噪聲電平的統計值產生明顯影響,這與前面的分析結論一致。
此外,表3 是在雷達不開發射機的條件下(此時系統僅有噪聲),采用該噪聲電平恒虛警后的系統虛警概率的變化情況。

表3 不開發射機時系統虛警率統計表
從表3 的數據來看,采用門限系數5 得到的虛警概率與理論分析結果基本吻合。
最后,在雷達開發射機的情況下,采取如下措施來驗證該噪聲電平恒虛警方法的效果。
在天氣晴朗且無風的條件下,雷達開機正常,信號處理器不加距離單元恒虛警[3],MTD 低頻濾波器0#、1#和15#濾波器加固定的雜波圖門限系數,此時,采集系統的虛警概率和MTD 中間濾波器噪聲統計值,其關系見圖4。從該圖上可以看到,雖然發射機工作使得接收機噪聲稍微變大,但系統的虛警概率沒有發生明顯變化,該基于MTD 中間濾波器噪聲統計的噪聲電平恒虛警處理方法在工程上的應用結果與分析是一致的。
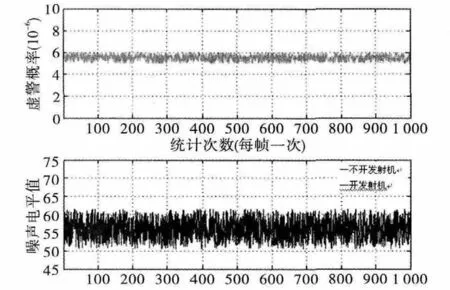
圖4 噪聲統計值及系統虛警概率變化趨勢圖
4 結束語
本文從工程應用角度出發提出了采用實時統計MTD 中間濾波器噪聲電平的方法,有效減小雜波對噪聲電平門限的影響,采用遞歸算法快速實現了雷達噪聲電平恒虛警。該方法已成功應用于某型雷達中。實踐證明,該方法實現簡單,效果良好,可進行推廣應用。
[1]張光義,趙玉潔.相控陣雷達技術[M].北京:電子工業出版社,2006.
[2]李宏等.雷達信號處理恒虛警性能的測試[J].計量與測試技術,2003(3):30-32.
[3]吳順君,梅曉春.雷達信號處理和數據處理技術[M].北京:電子工業出版社,2008.
[4]李穎,周輝.最大熵譜估計在預測雷達雜波中的應用[J].雷達與對抗,2001,(4):21-25.
[5]李靜威,吳桂生,察豪.對噪聲干擾的慢門限恒虛警處理分析[J].船舶電子工程,2008,28(4):106-108.
[6]王心福.雷達恒虛警處理對噪聲干擾的影響[J].電子對抗技術,2000,15(3):1-6.
[7]李蘊滋.雷達工程學[M].北京:海洋出版社,1999.
[8]肖開健,井偉等.基于DDS 的單脈沖體制雷達目標模擬的實現[J],電子科技,2011,24(11):13-15.

