差速驅動六輪導引車運動軌跡分析

暴海寧 宋 科 黎 原 馮艷麗 趙永亮 譚 旭

(中國航天科技集團第九研究院第十六研究所 西安 710100)

0 引言

AGV 是Automatic Guided Vehicles 的簡稱，屬于輪式移動機器人(WMR——Wheeled Mobile Robot)的一種。根據美國物流協會定義，AGV 是指裝備有電磁或光學自動導引裝置，能夠沿規定的導引路徑行駛，具有安全保護以及各種移載功能的運輸車。AGV 涉及機械、電子、光學、計算機等多個領域，廣泛應用于自動化物流系統中［1］。AGV 導引車的核心技術主要包括導引技術、導引控制避障技術和路徑規劃技術等，而路徑規劃則是以上核心技術的基礎性工作。優化路徑規劃可以在降低AGV 計算的復雜程度的同時，增加AGV 工作過程中的可靠性。AGV 運動的核心是驅動單元，由直流伺服電機，磁導引傳感器，傳動機構等組成。驅動單元通過前后端的磁導引傳感器獲取實時位置的引導信息，即驅動模塊與磁導引條的角度和位置偏差，通過微調跟蹤鋪設的磁條路徑行駛。同時磁導航因其鋪設成本低，路徑易于改變或擴充，差速驅動磁導航成為AGV 工業應用的一個重要方向值。文獻［2-3］基于全局運動學建模算法在路徑復雜時適應程度不高。文獻［4-5］研究的AGV 為驅動模塊與承載模塊剛性連接的傳統模型，驅動輪同時也是承載輪，導致在負載較大時對AGV 的路徑跟蹤控制難度加大。

本文討論的CASC-遠望號AGV 的牽引車驅動部分沿用差速驅動，其驅動模型如圖1所示。本體采用六輪車型結構，牽引驅動模塊安裝在車體下部，驅動模塊上部與車體柔性連接，下部跟蹤預先鋪設的的磁條行駛。車體前部兩個從動萬向輪起承重作用，車體后部兩個從動固定輪起承重和防止搖擺作用。依靠電機調速使兩驅動輪產生不同的線速度速度來實現轉向。文章在分析AGV 牽引車系統結構及運動原理的基礎上，描述了差速驅動AGV 牽引車車輪軌跡，并進行仿真驗證，研究了六輪AGV 行駛路徑情況。

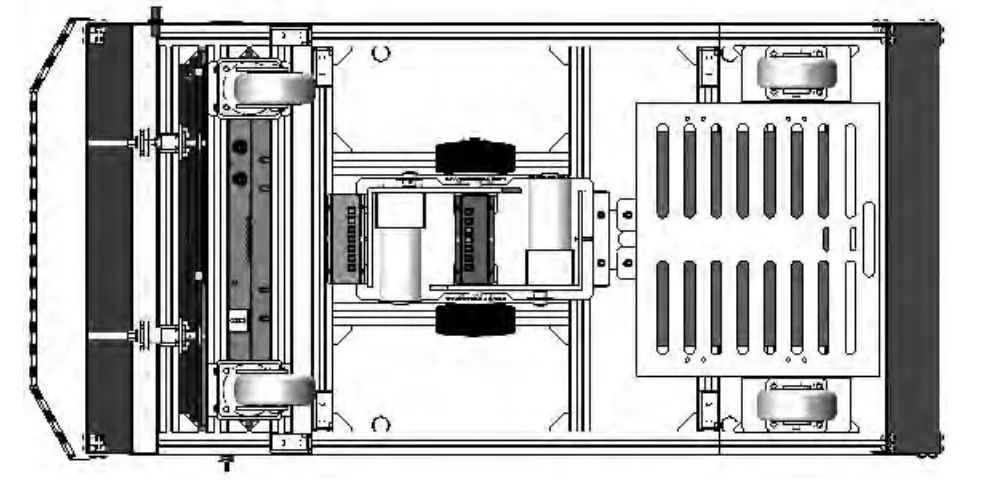
圖1 AGV 差速驅動模型

1 AGV 運動學分析

為了便于分析及建立CASC-遠望號AGV 運動方程，本文做出如下假設:整個AGV 車體關于其縱軸對稱;AGV 車體及所有車輪均為剛體;車輪在軌道平面做純滾動，無打滑，且所有車輪始終與地面保持接觸狀態。

AGV 車體的運動由直線運動和曲線運動兩部分構成，直線運動作為主要工作狀態，要求平穩可靠;曲線運動即AGV 的轉彎過程，作為輔助工作狀態，要求快速穩定。在生產中，直行過程AGV 可以通過磁導航傳感器實現微調，用RFID 標簽實現工作過程中的路徑選擇。

1.1 AGV 直行及微調過程分析:

本文中AGV 為差速驅動，E、F 為驅動輪，前輪A、B 為萬向輪，后輪C、D 為固定輪。在導引車行進過程中任取一點，其位置示意圖如圖2所示:

:AGV 行駛速度;

α:車體中心線與x 軸的正向夾角，即AGV 的方位角;

β:驅動輪EF 與車體中心線的夾角，即AGV 的轉向角;

γ:驅動輪行進方向與x 軸正向夾角;

H:AGV 的軸距

L:AGV 前后輪與驅動輪之間的輪距

G:后輪CD 軸線的中心

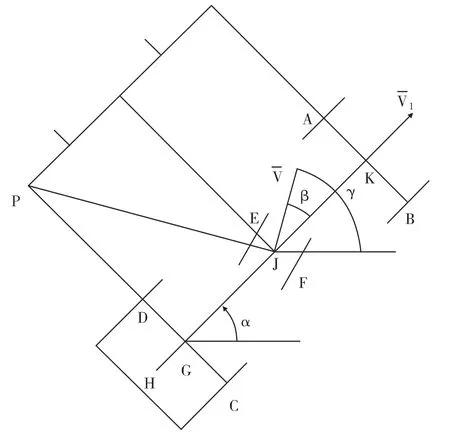
圖2 AGV 導引車運動模型

當前位置，AGV 的速度瞬心為P 點，在直線CD 與方向垂直的直線交點，根據圖2所示的幾何關系，有

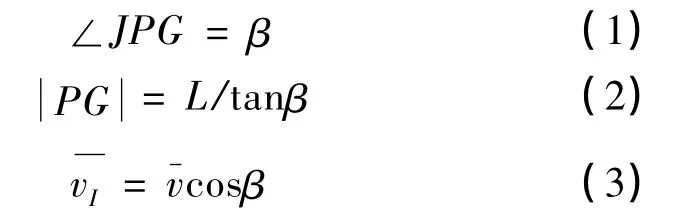
令驅動輪的轉向角速度為ωA，則其與車體中心線夾角為

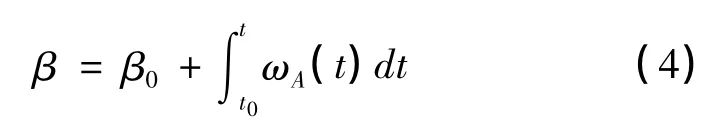
AGV 作為剛體相對于瞬心P 的角速度ω 為:

綜合上式可知:

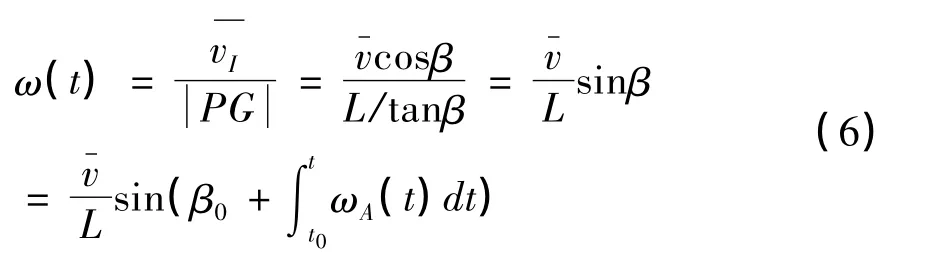
此時車體的中心線與X 軸正向夾角為:

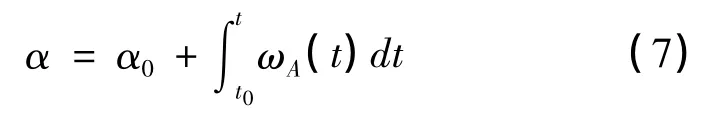
根據幾何關系，由圖可知，前輪與X 軸正向夾角為:

AGV 運動速度在X，Y 軸方向上的分量:

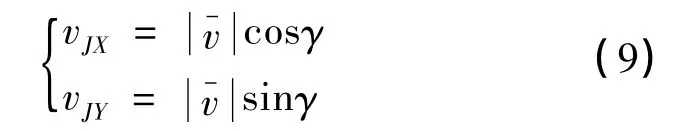
對速度進行積分可以得到驅動輪中心點J 的坐標方程為:

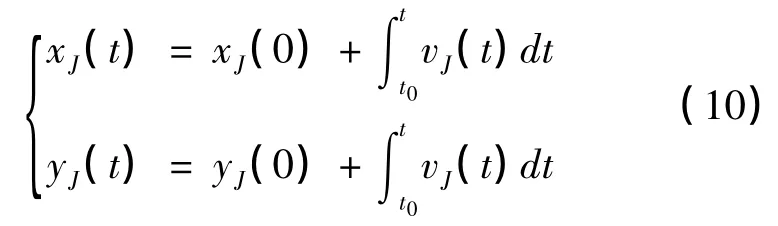
由式8、式9 可知:

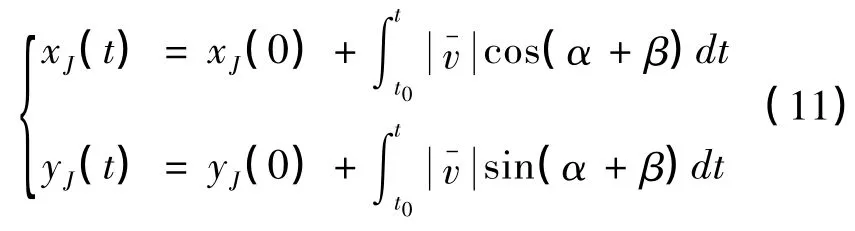
將式6，式7 帶入可得:

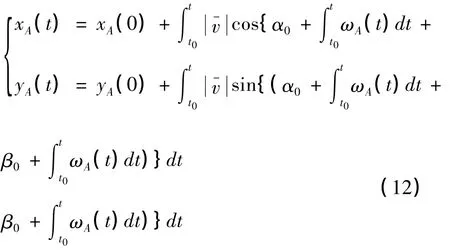
根據圖示的幾何關系，可以得到前后輪中心點的G 點，K 點的坐標方程為:

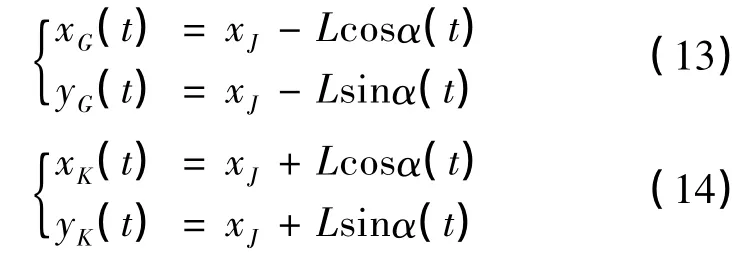
上式即為AGV 運動過程中的速度與軌跡的一般方程。其中四個輪子的軌跡方程為:

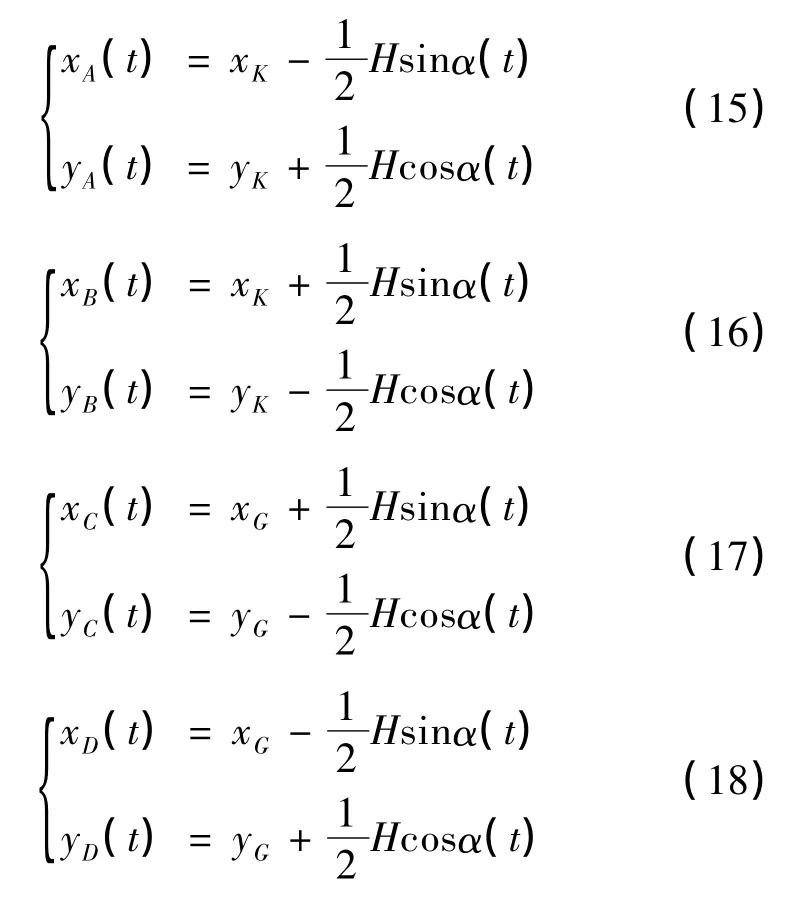
1.2 AGV 轉彎過程分析

若AGV 在t0時刻沿直線L1的方向行駛，通過轉彎過程，AGV 可以平穩的行駛到直線L2的方向上，如圖所示。令直線L1、L2的方程為:

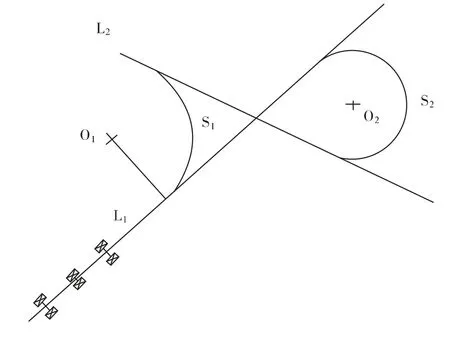
圖3 AGV 轉彎過程示意圖

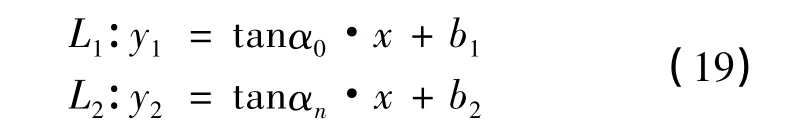
其中α0、αn，b1、b2分別為L1、L2的方位角和截距。鑒于AGV 是通過一段圓弧來完成它的平穩的轉彎過程，應確保該圓弧能夠與初始方向直線和目標方向直線均相切。針對已知的運動軌跡，其行駛直線、目標直線和轉彎半徑就是確定的。為了提高車體反應速度，減少計算量，在工程實際控制中，采用RFID 標簽選擇路徑，即在進入轉彎起點處之前增加RFID 電子標簽，設置左右優先權限，從而實現順時針、逆時針轉彎選擇問題。AGV 自身的轉彎過程只需知道其駛入彎道過程的起始點J 的坐標。當AGV 分別采用順時針和逆時針來實現轉彎過程時，其進入彎道的起始點是不同的，因此首先應該根據電子標簽的設定，讀取左右優先級狀態再判斷AGV 該采用何種轉彎方式，然后運用數學計算推導得出轉彎圓弧軌道的圓心坐標O。為了計算O 點的坐標，在L1和L2的基礎上構建參考平行直線L11和L22，并計算出L11和L22的交點，即O 點的坐標:

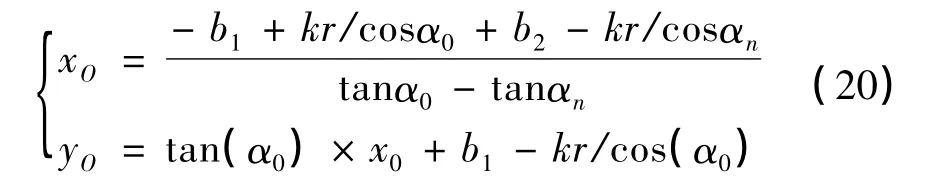
過圓心O 點做垂直于L1的直線，其與L1的交點E 點即為AGV 駛入彎道過程的起始點，通過聯立直線OE 和L1的方程，可以得到兩條直線的交點E點的坐標，即AGV 駛入彎道的起始點為:

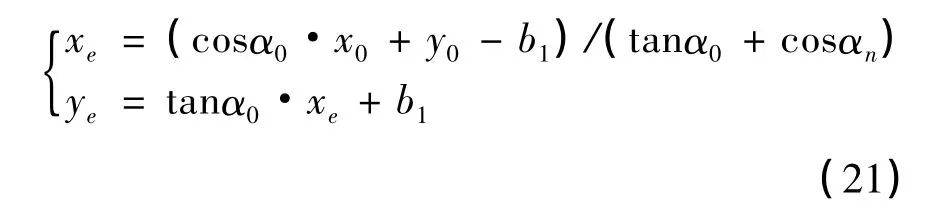
類似可知，在α0或者αn等于nπ/2(n 為任意整數)的情況下也可以得到AGV 駛入彎道的起始點。

2 運動仿真及實驗驗證

本文選擇使用Maple 軟件對AGV 運動過程進行運動仿真。在已經得到AGV 駛入彎道起始點的基礎上，采用積分方法可以得到驅動單元與車體的夾角，即導向角的大小。同時根據AGV 在運動過程中速度方程和預定軌道的方程就可以對AGV 在彎道行駛過程進行仿真驗證。

結合實際場地布置及使用功能要求，分別取直線L1、L2的截距b1=0 、b2=0，AGV 的行駛速度v=1m/s，轉彎半徑r=1m，軸距0.6m，轉向角初始值α0=π/6，αn=5π/6，β0=0 經過Maple 仿真，AGV 的轉向角β 的仿真結果及計算對比如圖4所示。其中虛線為仿真結果，實線為計算結果。實驗結果表明，該模型與AGV 運動實驗結果類似，證明所建立的模型與AGV 實際運動情況一致。

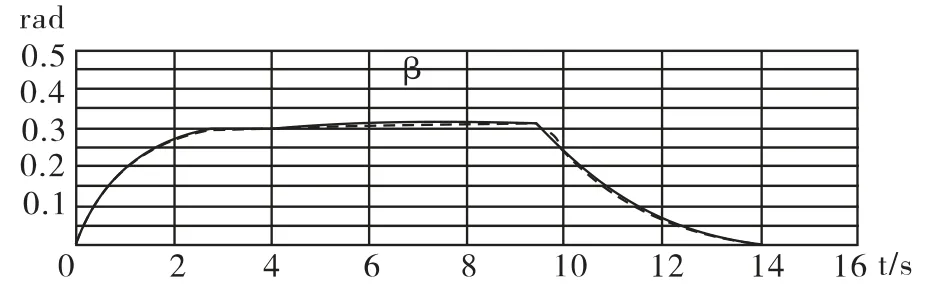
圖4 AGV 轉向角β 誤差對比

在模型正確的基礎上，保持初始值不變，可以得到車體中心線與X 軸正向夾角α 和前輪與車體中心線夾角β 的曲線。

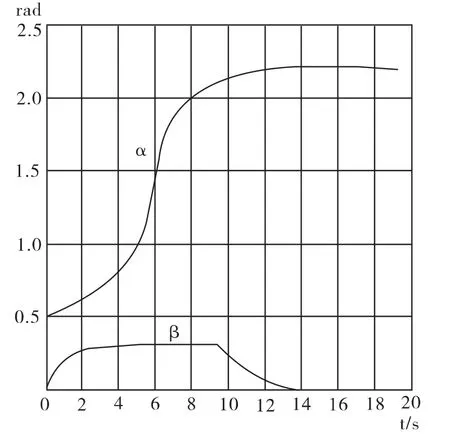
圖5 AGV 方位角α 和導向角β 曲線

由圖5 可以看到導向角β 曲線變化可以分為三個過程:

1)從0s 到2s 的過程中，導向角β 由0 開始逐漸增大，方位角α 也在隨之逐漸增加，AGV 磁導航裝置進入圓弧軌道，開始轉彎階段。

2)從2s 到9s 的過程中，β 保持不變，由公式(5)分析可知，此時AGV 以恒定的角速度ωA行駛在預定的軌道上，AGV 進入了穩定的轉彎階段。

3)從9s 到14s 階段，β 逐漸減小直至最終到0的過程中，AGV 沿著軌跡逐漸駛出彎道，方位角α持續增加。當β=0 時，α=αn，AGV 平穩駛出圓弧軌道，結束轉彎階段。

為了了解AGV 整體在預定軌道上的行駛狀況，研究軌跡誤差，對AGV 整車進行運動過程分析，得到前后兩對承重輪及驅動輪的運動軌跡方程，由圖6 可知，AGV 能能夠很好的完成整個轉彎過程，整體運行平穩，跟蹤路徑準確。

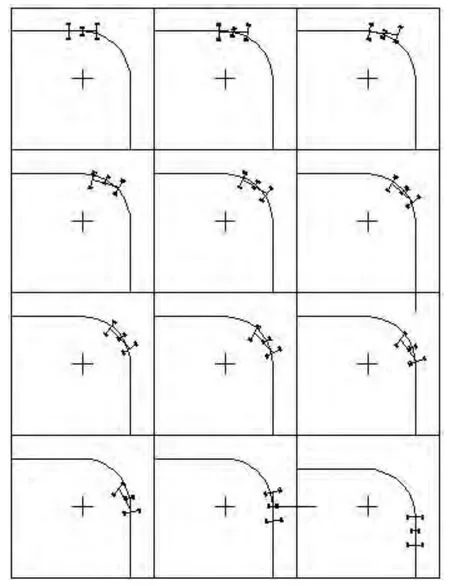
圖6 AGV 整體轉彎過程軌跡

3 總結

本文對差速驅動六輪導引車進行運動過程分析，建立了車體與所跟蹤路徑的位置關系模型，計算出AGV 運動過程中軌跡與運動的一般方程，分析了差速驅動裝置工作中車體驅動輪和承重輪的軌跡問題。然后對AGV 的轉彎過程進行了分析，并根據車體的幾何尺寸及預定軌道的半徑，計算出了AGV 開始轉彎過程的起始點，并且用MAPLE 進行編程，仿真得到AGV 在轉彎過程中的方位角和導向角的變化曲線以及六個輪子的軌跡。實驗中車體位姿驗證了模型的正確性，為六輪自動導引車行駛路徑提供了可參考的模型和算法，AGV 車體行駛軌跡為車體結構設計和磁導航軌道的鋪設提供一定的理論支持。

［1］武星，樓佩煌，唐敦兵.自動導引車路徑跟蹤和伺服控制的混合運動控制［J］.機械工程學報，2011，47(3):43-48.

［2］沈穎.激光導引AGV 車載控制系統研究［D］.合肥:合肥工業大學.2007.

［3］錢曉明，吳斌武星，樓佩煌.潛入牽引式自動導引車運動特性分析［J］.農業機械學報，2014，4(2):29-30.

［4］劉沙沙，魏生民，薛瀛，汪焰恩。基于視覺引導AGV 路徑跟蹤模糊控制研究［J］.機床與液壓2009，8:32-86.

［5］孟琦，金亞萍，耿牛牛，史偉偉，許鵬鵬.基于磁線導引的雙轉向架驅動AGV 應用研究［J］制造業自動化.2014，8:40-44.

［6］周馳東，樓佩煌，王輝，張炯.移載式磁導航AGV 關鍵技術研究［J］.工業控制計算機.2012，1:22-25

［7］賀長林，史恩秀.基于雙目立體視覺和側向路徑的AGV 導航技術研究［D］.西安:西安理工大學.2008.