電磁感應加熱系統負載感應器研究*
楊偉福,曹廣忠,邱 洪,李寒逸,王 鑫(深圳大學深圳電磁控制重點實驗室,廣東深圳 518060)
電磁感應加熱系統負載感應器研究*
楊偉福,曹廣忠,邱洪,李寒逸,王鑫
(深圳大學深圳電磁控制重點實驗室,廣東深圳518060)
摘要:針對電磁感應加熱系統加熱不均勻的問題,提出了改進型電磁感應加熱系統并探討其負載感應器的加熱性能。基于An?soft Maxwell 2D,建立了傳統型及改進型的電磁感應加熱系統負載感應器有限元模型,采用二維渦流場分析方法對建立的兩種有限元模型進行了熱性能仿真分析,探討了兩種電磁感應加熱系統負載的渦流損耗分布。研究結果表明,提出的改進型電磁感應加熱系統具有更高效的加熱性能和均勻加熱的特點。
關鍵詞:改進型負載感應器;有限元法;二維渦流場;熱分布
*國家自然科學基金資助項目(編號:51275312);深圳市科技計劃項目(編號:JSGG20141015153303491,JCYJ20140418182819160)
0 引言
電磁感應加熱系統負載感應器由感應加熱線圈與被加熱負載組成,可等效為電阻和電感的串聯。電磁感應加熱系統遵循電磁感應、集膚效應和熱傳導三大基本原理,其負載感應器基于電磁場與熱場的強耦合場工作,且極易受溫度變化影響,因此負載感應器是一個復雜的強非線性系統。國內外學者已對電磁感應加熱系統負載感應器進行了一系列有價值的研究工作,主要集中于結構優化、等效電感和等效電阻模型等研究。
L.C.MENG[1]等人基于電磁感應加熱系統負載感應器的磁場分析,采用三維有限元分析法,對感應加熱線圈進行了結構分析及優化設計;Mah?di Hediehloo[2]等人針對感應加熱線圈的渦流損耗,采用有限元分析法,分析了感應加熱線圈的集膚效應和鄰近效應,優化設計了感應加熱線圈的結構;劉元柱[3]采用三維渦流場有限元分析法,初步分析了感應加熱線圈的磁條、材料特性、結構對輸出功率、溫度分布、電磁泄漏等方面的影響;D.Sinha[4]提出了雙線盤的感應加熱線圈,研究了被加熱負載與感應加熱線圈的間隙、被加熱負載材料與控制頻率之間的關系,比較分析了雙線盤與單線盤的結構;S.H.Hosseini[5]、P.Hernan?dez[6-7]、J.Aeero[8-14]等人研究分析了家用電磁感應加熱系統感應加熱負載,通過數值仿真優化了感應加熱線圈結構、感應加熱線圈與被加熱負載的間隙、磁條位置等,提出了最優負載感應器結構。
本文基于Ansoft Maxwell 2D,采用二維渦流場分析方法,建立了電磁感應加熱系統負載感應器的有限元仿真模型,分析了傳統型加熱負載器作用下負載的歐姆損耗情況等熱特性,基于傳統單層加熱負載器的分析,設計了改進型加熱負載器,并比較分析了傳統型和改進型兩種加熱負載感應器的熱特性。
1 渦流場理論
麥克斯韋方程組是支配所有宏觀電磁現象的一組基本方程,其微分形式表達為[15]:

在線性、均勻、各向同性媒質中,場量間的結構關系為:

由麥克斯韋方程組計算可得:

由于渦流場為時間簡諧場,因此磁場強度H、磁感應強度B、電場強度E和電流密度J均為時間的余弦函數。為了方便分析,上述各量可用相量表示,由式(8)可得:

在正弦時變場的前提下,式(9)即為求解渦流場的復矢量微分方程。
在Ansoft Maxwell 2D中,阻抗矩陣的計算分為電感矩陣和電阻矩陣兩部分,完成兩部分矩陣計算后,將它們合成為阻抗矩陣。
(1)電感計算
為了計算電流環的電感,計算場解之后,再計算系統的平均能量:

式(10)中,H?為磁場強度的共軛值。
電感矩陣可表達為:

(2)電阻計算
渦流問題求解后,采用計算系統的歐姆損耗的方法計算電流環的電阻,歐姆損耗的表達式為:

式(12)中,J*為自由體電流密度的共軛值。
電阻矩陣可表達為:

2 負載感應器有限元分析
相對于ANSYS等渦流場計算軟件,Ansoft Maxwell 2D具有使用簡單,參數提取方便,可視化好等優點,尤其是其渦流場的計算精度高[15]。本文采用Ansoft Maxwell 2D對負載感應器進行建模與仿真分析。
2.1負載感應器有限元建模
負載感應器的等效電感和等效電阻與流過感應加熱線圈的電流工作頻率、被加熱負載的相對導磁率、透入深度、感應加熱線圈與被加熱負載的耦合系數M等因數有關。考慮實際情況,本文給定激勵源的工作頻率f=20 kHz,I=10 A,材料則選擇為不銹鋼(Ur=1)、厚度d=2 mm的被加熱負載,被加熱負載與感應加熱線圈的間隙h=2 mm,感應加熱線圈的匝數n=20,單股線圈的截面積Sc=36 mm2,傳統型系統為單層線圈,圈數N=12;改進型系統為雙層線圈,圈數N=14。負載感應器的示意圖如圖1、圖2所示,其中Rg=110 mm,Rc1=20 mm,Rc2=100 mm,a=6 mm,h1=0.727 3 mm(即線圈可視為緊密靠近)。
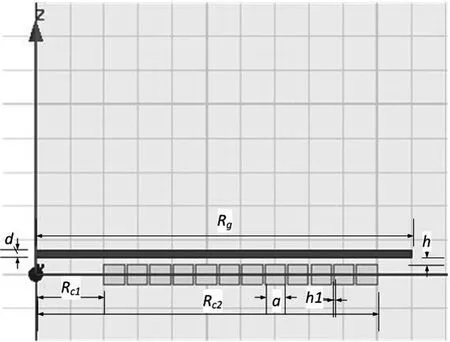
圖1 傳統負載感應器示意圖
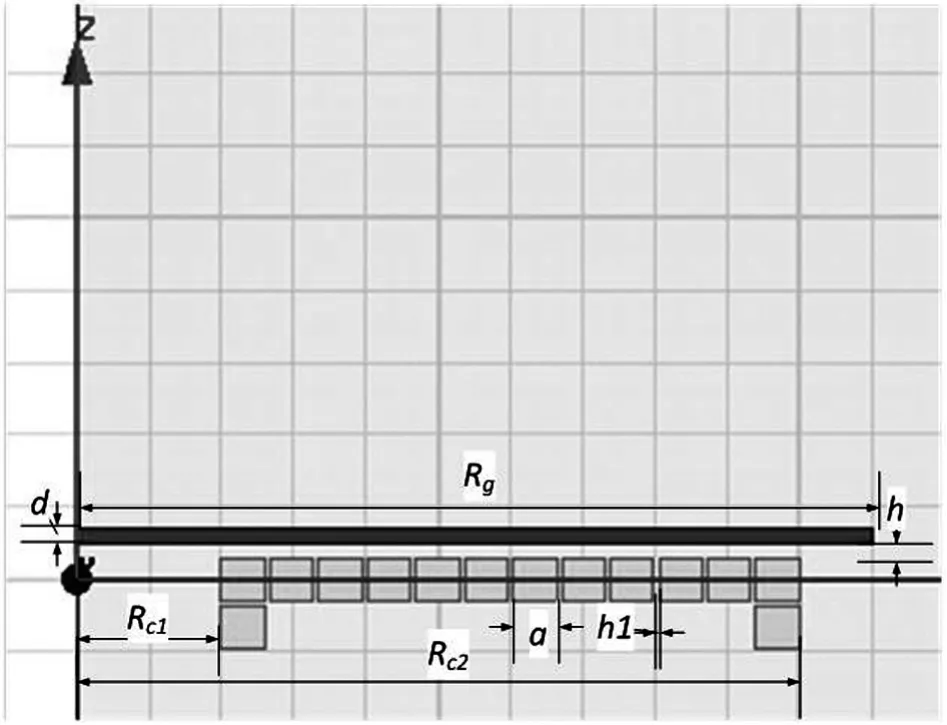
圖2 改進型負載感應器示意圖
2.2負載感應器有限元仿真
基于Ansoft Maxwell 2D,在設置好前處理相關參數后,選取渦流仿真器進行仿真,對仿真結果進行后處理,得到負載感應器歐姆損耗等相關結果,如表1、圖3所示。
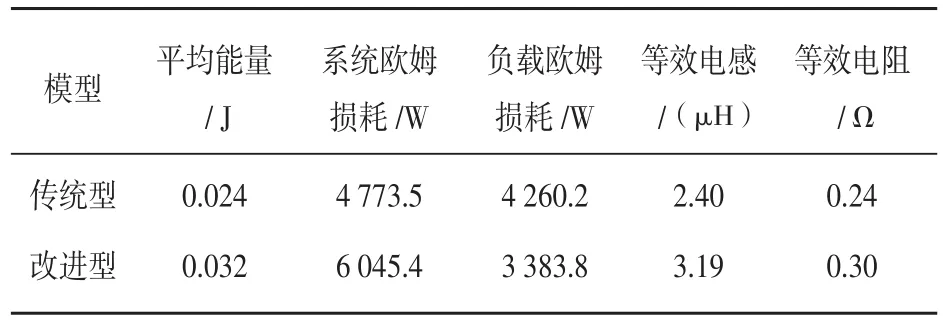
表1 系統的等效電感及等效電阻等場量

圖3 兩種負載感應器歐姆損耗比較
由表1可知,相同激勵時,改進型電磁感應加熱系統的加熱效率比傳統型電磁感應加熱系統高,而兩個系統的等效電感和等效電阻則相差不大,故基于同一硬件系統,傳統型和改進型電磁感應加熱系統負載感應器均能夠穩定工作,且改進型電磁感應加熱系統加熱效率高。
由圖3可知,相同激勵時,改進型感應加熱系統負載感應器的歐姆損耗比傳統型感應加熱系統負載感應器的歐姆損耗分布更加均勻。傳統型感應加熱系統負載感應器的歐姆損耗主要分布在Rg=40mm~80mm的區域,且分布不均勻,故加熱不均勻。改進型感應加熱系統負載感應器的歐姆損耗主要均勻分布在Rg=20mm~100mm的區域內,即加熱線圈的分布區域相對應的負載能夠均勻、高效地加熱。
綜上所述,改進型電磁感應加熱系統比傳統型電磁感應加熱系統更高效均勻加熱。
3 實驗結果討論
基于仿真分析,繞制線圈,將制作好的傳統型和改進型線圈接入同一硬件電路,并加入負載,即鍋具。實驗裝置如圖4所示。

圖4 電磁感應加熱實驗裝置
基于同一硬件電路,在接入不同的加熱線圈后,其諧振電路的諧振情況,即系統的電流輸出情況分別如圖5、圖6所示。其中圖5為硬件電路接入傳統型線圈后,在輸出功率為2 kW時,系統的電流輸出波形;圖6為硬件電路接入改進型線圈后,在輸出功率為2 kW時,系統的電流輸出波形。
由圖5及圖6知,在接入傳統型和改進型線圈進行加熱時,系統的輸出電流波形基本呈正弦,即系統穩定工作。
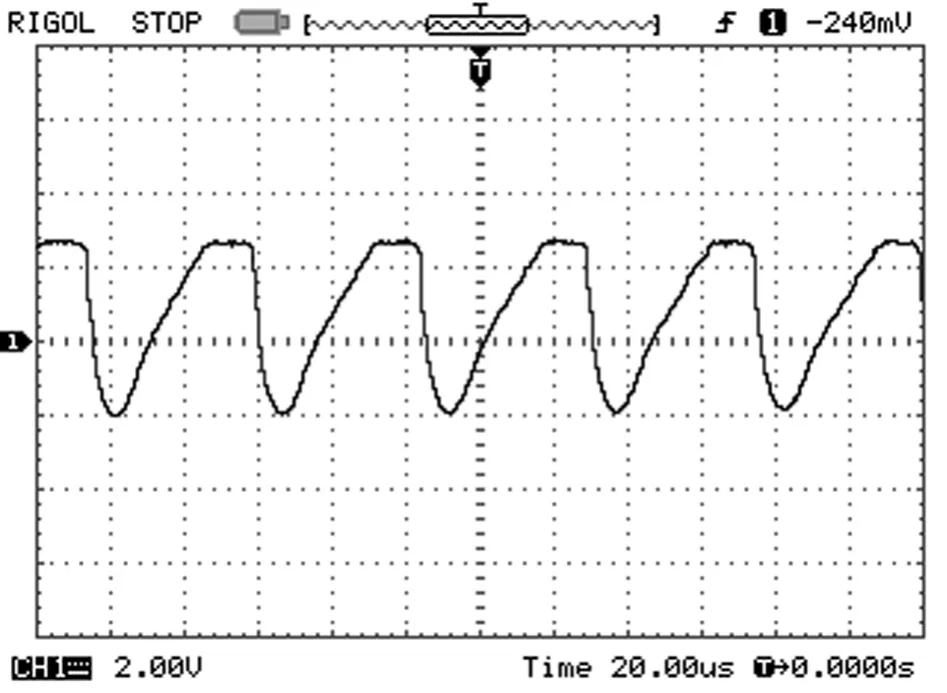
圖5 傳統型感應加熱系統的電流輸出波形

圖6 改進型感應加熱系統的電流輸出波形
在系統功率為2 kW時,兩種加熱系統負載的熱分布情況分別如圖7、圖8所示。
由圖7、圖8可以看出,沿圖中所繪相同直徑,傳統型電磁感應加熱系統負載的溫度的最大值為123.5°F,最小值為80.5°F,平均值為107.9°F;改進型電磁感應加熱系統負載的溫度的最大值為116.9°F,最小值為83°F,平均值為105.7°F。在加熱到相同溫度時,改進型感應加熱系統比傳統型感應加熱系統的熱分布更加均勻。

圖7 傳統型加熱系統負載的溫度變化

圖8 改進型加熱系統負載的溫度變化
在系統功率為2 kW,加熱2 s時,兩種加熱系統負載的熱分布情況分別如圖9、圖10所示。

圖9 傳統型加熱系統負載的溫度分布

圖10 改進型加熱系統負載的溫度分布
由圖9和圖10可得,沿圖中所繪相同直徑,在系統功率為2 kW,加熱2 s時,傳統型電磁感應加熱系統負載的溫度的最大值為123.5°F,最小值為80.5°F,平均值為107.9°F;改進型電磁感應加熱系統負載的溫度的最大值為147.2°F,最小值為85.8°F,平均值為126.2°F。改進型電磁感應加熱系統比傳統型電磁感應加熱系統更加高效。
4 結語
針對傳統電磁感應加熱系統加熱不均勻的缺點,基于Ansoft Maxwell 2D,分析了感應加熱負載器的電磁特性,優化設計了一種改進型線圈,對具有不同類型加熱線圈的電磁感應加熱系統進行了被加熱負載熱分布的研究,研究結果表明改進型和傳統型兩種電磁感應加熱系統都具有較好的諧振性能,改進型電磁感應加熱系統具有更加高效的加熱性能和加熱更均勻的特性。
參考文獻:
[1]L.C.Meng,K.W.E.Cheng,K.W.Chan.Heating Perfor?mance Improvement and Field Study of the Induction Cooker[C].The 3rd International Conference on Power Electronics Systems and Applications,Hong Kong,2009:1-3.
[2]Mahdi Hediehloo,Mahdi Akhbari.New approach in de?sign of planar coil of induction cooker based on skin and proximity effects analysis[C].IEEE International Con?ference on Industrial Technology,Australia,2009:1-6.
[3]劉元柱.三維渦流場有限元分析與應用[D].成都:電子科技大學,2007.
[4]D.Sinha,P.K.Sadhu,N.Pal,et al.Computation of In?ductance and AC Resistance of a Twisted Litz-Wire for High Frequency Induction Cooker.2010 International Conference on Industrial Electronics[C].Control and Robo- tics,2010:85-96.
[5]S.H.Hosseini,A.M.Kashtiban,GAlizadeh.Particl-e Swarm Optimization and Finite-Element Ba- sed Ap?proachforInductionHeatingCookerDesign.SICE-ICASE,2006,International Joint Conference [C].2006:4624-4627.
[6]P.Hernandez,F.Monterde,J.M.Burdio.Power loss opti?misation of foil coils for induction cooking.Industrial Electronics Society(IECON),1998,Proeeedings of the 24th Annual Conference of the IEEE[C].1998:371-374.
[7]P.Hernandez,F.Monterde,J.M.Burdio,et al.Power losses distribution in the litz-wire winding of an inductor for an induction cooking appliance.Industrial Electronics Society(IECON),2002,28th Annual Conference of the IEEE[C].2002:1134-1137.
[8]J.Aeero,R.Alonso,J.M.Burdio,et al.Enhanceme- nt of induction heating Performance by sand- wiched Planar windings[J].Electronics Letters,2006,42(4):241-242.
[9]J.Acero,R.Alonso,J.M.Burdio.A model of losses in twisted-multistranded wires for Planar windings used in domestic induction heating appliances.Applied Power ElectronicsConference(APEC)[C].2007:1247-125.
[10]J.Acero,J.M.Burdio,L.A.Barragan,et al.A model of the equivalent impedance of the coupled winding load system for a domestic induction heating application.IEEE International Symposium on Industrial Electronics (ISIE)[C].2007:491-496.
[11]J.Acero,J.M.Burdio,L.A.Barragan,et al.An electromagnetic-based model for calculating the efficiency in domestic induction heating appliances.Power Electronics Specialists Conference(PESC)[C].2006:l-6.
[12]J.Acero,J.M.Burdio,L.A.Barragan,et al.Modeli- ng and Calculation of the Efficiency for Low-cost Round-wire Planar Windings in Domestic Induction Heating Applications.Power Electronics Specialists Con?ference(PESC),2007:1411-1416.
[13]J.Acero,R.Alonso,L.A.Barragan,et al.Magnetic vec?tor potential based model for eddy-current loss calcula?tion in round-wire planar windings[J].IEEE Transac?tions on Magnetics,2006,42(9):2152-2158.
[14]J.Acero,P.J.Hernandez,J.M.Burdio,et al.Simple re?sistance calculation in litz-wire Planar windings for in?duction cooking appliancees[J].IEEE Transactions on Magnetics,2005,41(4):1280-1288.
[15]徐應年.感應加熱電源負載感應器模型與恒頻調功研究[D].武漢:華中科技大學,2009.
(編輯:向飛)
Study on Load Inductor of Electromagnetic Induction Heating System
YANG Wei-fu,CAO Guang-zhong,QIU Hong,LI Han-yi,WANG Xin
(Shenzhen Key Laboratory of Electromagnetic Control,Shenzhen University,Shenzhen518060,China)
Abstract:Aiming at the problem of uneven heating of electromagnetic induction heating system,an improved electromagnetic induction heating system is put forwarded and performance of the heating load Inductor is discussed in this paper.Based on Ansoft Maxwell 2D,Finite element models of the traditional and modified load inductor of electromagnetic induction heating system are established,the two-dimensional eddy field analysis method is utilized simulate for the two finite element models,The eddy current loss distribution of two kinds of loads of the electromagnetic induction heating system is investigated.The results show that the proposed improved electromagnetic induction heating system has a more efficient heating performance and an uniform heating characteristic.
Key words:improved load inductor;finite element method;2D eddy current field;heat distribution
作者簡介:第一楊偉福,男,1988年生,廣東人,碩士研究生。研究領域:電磁控制理論。
收稿日期:2015-01-09
DOI:10.3969/j.issn.1009-9492.2015.07.025
中圖分類號:O441.3
文獻標識碼:A
文章編號:1009-9492 (2015 ) 07-0081-05

