讓學生主動探究，提升課堂效能

吳雅芳

[摘 要] 根據新課標的要求，教師要發揮學生的主體性，讓學生主動參與課堂探究，提升課堂思維效能. 本文從教學實踐入手，提出激發學生探究熱情、發展探究能力的教學策略.

[關鍵詞] 小學數學；課堂探究；思維效能新課標明確指出，教師要充分發揮學生的主體性，將課堂還給學生. 根據這一理念，各種課改實踐如火如荼，開展迅速，然而在實際教學中，教師生怕學生不能自主思考問題，代替學生分析、代替學生操作的現象并不鮮見. 這樣的教學模式，剝奪了學生自主參與課堂實踐的機會，導致課堂思維效能減弱，限制了新課標理念的進一步推進.

著名教學家葉圣陶先生曾經指出，給學生提供自主探索的機會，才能最大限度發揮學生的潛能，實現課堂教學的高效性和有效性. 在小學數學教學中，教師可以根據教材內容，設置有效的數學活動，立足學生主體的特性，讓學生主動參與數學探究，深入理解數學概念，全面建構數學知識，提升課堂教學的思維能力. 這是最根本的問題. 那么，在小學數學教學中，教師該如何發揮學生潛能，使其主動探究呢？筆者現根據自己的教學實踐，談談體會和思考.

聯系實際，激發探究興趣

日本數學家米山國臧曾經指出，數學的本質，就是要解決與生活密切關聯的問題. 在小學數學教學中，教師可以根據生活實際，設置學生感興趣的數學情境，讓學生將數學與現實掛鉤，激發探究興趣，由此展開數學探究.

例如，在教學蘇教版小學數學“找規律（一一間隔排列）”這一內容時，教學重點是要讓學生找出間隔排列的兩種物體個數之間的關系，學會應用間隔規律解決問題. 為了讓學生深入生活現象，發現數學規律，筆者特意設置了這樣的數學情境：1. 出示有關城市廣場路燈排列的兩幅情境圖（有橢圓形，有心形的，兩端都是橢圓形），讓學生思考：觀察圖中路燈的排列，你發現了什么？有什么規律？學生通過觀察，很快就發現了問題所在：路燈是按照一個橢圓、一個心形、一個橢圓、一個心形的方式依次排列的，這里有一個規律：必須是兩個物體，而且是兩個物體一個隔著一個進行排列. 由此，筆者讓學生按照這樣的排列，從生活中尋找類似的現象：生活中還有哪些類似的排列？你能舉例說明嗎？學生認為，像這樣的排列形式，生活中還有很多，比如地板上的花紋裝飾，按照棱形、圓形、棱形、圓形的方式依次排列，比如公園花帶里的花，會按照紅色、藍色、紅色、藍色依次排列，再比如學校舉行廣播操比賽，通常會按照男生、女生、男生、女生的隊形來排列. 筆者指出這種排列方法就叫做一一間隔排列，并讓學生明確兩個要素（兩個物體，一個隔一個排列），接下來繼續出示生活中的現象：墻面瓷磚（兩端都是紅色）紅色、藍色、藍色、紅色，木樁和籬笆的排列（兩端都是木樁）籬笆、木樁、籬笆、木樁，還有果盤擺放（兩邊都是橘子）橘子、蘋果、橘子、蘋果等，讓學生進行判斷和分析，從而積累豐富的表象，深入理解一一間隔排列的規律，建立深刻的認知.

以上教學活動，教師由生活現象入手，創設了學生熟悉的課堂情境，激發學生的探究興趣，指導學生從數學的角度分析生活現象中蘊涵的數學規律，讓學生初步感知間隔排列的基本特點，在此基礎上展開探究，讓學生根據已有經驗，逐步積累了感性認識，深入理解一一間隔排列的數學規律，從而大大提升了課堂效率.

搭建平臺，推進自主探究

根據新課標的要求，教師要扮演的角色，是充當學生學習活動的組織者和合作者，因而在數學教學中，要給予學生尊重，搭建一個自由交流的平臺，根據學生的具體問題，在認知沖突處探究，在思維阻塞處進行疏導，由此促進學生的思維發展.

1. 疏導認知沖突

數學認知理論認為，學習的過程是一個認知逐步被同化和異化的過程，學習者根據已有的舊知進行新知吸收，隨著認知結構的沖突出現，學生被激發起探究的心理需求，想要找到問題的答案. 此時，正是教師進行引導探究的最佳時刻.

例如，在教學“用字母表示數”這一內容時，學生存在的主要難點在于，之前的思維定式是計算式必須是數字加運算符號，現在要變成字母加數字，這就形成了認知沖突，接受和理解這一新的數學運算形式，顯然需要一個轉變的過程. 為了讓學生深刻理解抽象字母所代表的數學含義，筆者做了這樣的問題設置：哥哥比小明大2歲，那么小明1歲的時候，哥哥幾歲？小明是5歲，哥哥幾歲？學生根據題意，很快列出算式：小明1歲，哥哥是1+2=3（歲）；小明5歲，哥哥是5+2=7（歲）. 筆者繼續提問：想一想，假設小明的歲數是固定的數字，你怎么計算哥哥的年齡呢？學生提出，小明15歲，哥哥是17歲；小明17歲，哥哥是19歲；小明19歲，哥哥是21歲……此時筆者追問：如果用一個算式來表示，怎么表示呢？學生這才從定式思維中走出來，提出用一個字母來表示小明的歲數，比如a，那么哥哥的年齡就是a+2. 此時筆者繼續追問：假如哥哥的年齡是固定的數字，那么小明的年齡怎么用算式表示？學生提出，假設哥哥的年齡為b，那么小明的年齡就是b-2. 通過這樣的疏導，學生突破了原有的認知誤區，從具體的數字化思維逐步過渡到抽象的算式思維，由個別實現了共性，從而有效突破抽象，建構新知.

2. 點撥思維歧途

小學生由于缺乏獨立思考的能力，暗示性較強，往往容易受到已有知識和經驗的負遷移，這既是學習的優勢，又是弱點所在. 教學中，教師要牢牢把握學生的認知方向，以防止南轅北轍，在學生偏離思維航向時進行引導，通過探究走出思維歧途，引向思維的正道.

例如，在教學蘇教版四年級內容“能被3整除的數的特征”時，筆者先學生復習鞏固了能被2和5整除的數的特征，由此學生對能被3整除的數的特征有了猜測，認為個位數是3的數就能被3整除. 到底事實是否如此呢？為了預防學生誤入歧途，筆者讓學生進行驗證：你能舉出相關的例子來證明，個位上是3的數就能被3整除嗎？你還能舉出相關的例子來證明，個位上不是3的數也能被3整除嗎？學生立刻展開了討論，結果發現，個位上不是3的數（比如2，1，0，5，7等）也能被3整除，由此可以得出，個位上是否是3并不是根本要素. 那么，能被3整除的數到底有什么特征呢？學生提出可以將100以內能被3整除的數寫出來，看看有什么特點.

通過有效引導，學生通過自主探究，有效規避了思維盲區，走出了正確的探究之路，深入理解了數學概念，推動了數學問題的有效解決.

引導辨析，深化自主探究

數學思維的本質，是要能夠靈活應對，進行問題分析，從而實現問題的有效解決. 這個過程正是培養學生自主探究的過程，也是學生容易出現思維分歧的過程，這需要教師的引導辨析，讓學生去偽存真，深刻理解數學概念的本質內涵，并獲得數學思維的內化.

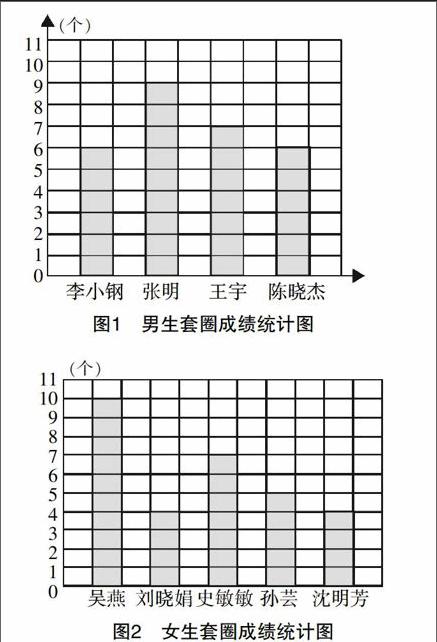
例如，在教學蘇教版五年級內容“統計”時，筆者讓學生根據統計圖判斷男女生套圈的準確率，看看到底哪一組最高（如圖1、圖2）. 學生分為兩組，進行了激烈的爭論，為此筆者引導展開辯論，先讓學生驗證自己的猜想，然后根據驗證結果來證明自己的答案.

由此，學生提出了兩種方案，一種通過移動圖示的方法，將男生中的張明套的圈數給李小鋼移1個，再給陳曉杰移1個，這樣三個人就和王宇一樣多，都是7個；女生中同樣采用這樣的方法，將套圈多的吳燕、史敏敏進行移動，這樣每個人套6個，這樣一來，就可以進行直觀的男女生比較，一眼就看出了分曉；另一種方案是平分差，就是將男生中比李小剛多的圈拿出來平分，女生中比劉曉娟多的圈拿出來平分，根據多的圈平分后的結果進行比較. 那么，如何才能算出男女生平均每人的成績呢？學生根據之前的討論，認為可以采用求和平均的方法來進行計算，有效完成了對新知的建構.

以上教學中，針對學生的爭辯教師并沒有給出結論，而是通過有效的引導，啟發學生自主探究，通過驗證猜想，進行推斷和分析，在思維的碰撞中，提升學生思考的深度和廣度，使學生的思維能力得到有效的培養.

總之，在小學數學教學中，教師要以學生為主體，設計有效的教學活動，把握課堂時機，發揮教師的主導作用，培養學生自主探究的能力. 只有學生成為課堂的主角，展開有效探究，才能推動課堂教學的深入發展，以此促進數學課堂的高效化. 這正是小學數學課堂改革的關鍵所在.