彈體侵徹剛玉塊石混凝土復合靶體的數值分析

方 秦,羅 曼,張錦華,孫志遠

(解放軍理工大學,江蘇 南京 210007)

?

彈體侵徹剛玉塊石混凝土復合靶體的數值分析

方 秦,羅 曼,張錦華,孫志遠

(解放軍理工大學,江蘇 南京 210007)

在先前混凝土三維細觀模型和塊石遮彈層三維模型研究的基礎上，研究了小直徑炸彈侵徹條件下，剛玉塊石遮彈層的抗侵徹性能。重點分析了彈體侵徹條件對侵徹深度和彈體偏轉角度的影響以及遮彈層構造參數對侵徹結果的影響；詳細探討了彈體命中速度、命中角度和彈著點位置，以及剛玉塊石大小、體積率和填充混凝土強度對遮彈層抗侵徹性能的影響。與普通塊石遮彈層相比，剛玉塊石混凝土復合遮彈層具有更好的抗彈體侵徹性能。

爆炸力學；抗侵徹；三維模型；剛玉塊石

巖石由于強度較高、抗侵徹性能較好，且具有取材方便、施工工藝簡單等特點，作為防護工程材料，一直為人們所關注。C.F.Austim等[1]、M.D.Gelman等[2]、B.Rohani[3〗對塊石遮彈層的抗侵徹性能進行了大量的研究；H.Langheim等[4]也開展了一系列塊石遮彈層抗彈體侵徹實驗研究，結果表明，塊石遮彈層對抵抗彈體侵徹具有很好的防護效果。唐德高等[5]對剛玉塊石靶體的抗侵徹性能進行了實驗研究，發現剛玉塊石是一種很好的抗侵徹材料。剛玉石[6]的主要成分是AL2O3，密度為3 800 kg/m3，彈性模量為400 GPa，與普通石頭相比，其硬度和強度極高，且具有抗沖擊、耐高溫等特點。因此，深入研究剛玉塊石混凝土復合遮彈層的抗侵徹性能，對提高防護工程的生存能力具有重要意義。

目前，對于剛玉塊石遮彈層抗侵徹性能的研究，主要以實驗研究為主，已經取得了一定的研究成果[5]。眾所周知，高速侵徹實驗研究一方面需要花費大量的人力物力，另一方面實驗研究只能獲得宏觀的結果，無法深入細致地研究侵徹過程的作用機理，且實驗過程影響因素較多。由于剛玉塊石遮彈層中塊石大小、形狀以及空間位置分布具有隨機性等特點，其對侵徹彈體的作用機理極其復雜，必須借助于數值方法，才能揭示剛玉塊石混凝土復合遮彈層的抗侵徹性能。本文中，基于前期的三維隨機骨料生成算法和塊石遮彈層生成算法[7-8]，針對剛玉塊石大小、形狀以及空間分布的隨機性特征，建立在結構方面與實際剛玉塊石遮彈層相似的三維分析模型，采用LS-DYNA動力學分析軟件，研究剛玉塊石的隨機分布特性對彈體侵徹過程中偏轉角度和侵徹深度的影響，討論剛玉塊石體積率、填充混凝土強度、彈體命中角度與位置、彈體命中速度等因素對剛玉塊石混凝土復合靶體抗侵徹性能的影響。

1 剛玉塊石混凝土復合遮彈層的三維有限元分析模型

1.1 模型的建立

剛玉塊石混凝土復合遮彈層在內部結構組成方面有如下特征：一是組成遮彈層的剛玉塊石大小及形狀具有隨機性；二是遮彈層在形成過程中，剛玉塊石在復合遮彈層內空間分布位置具有隨機性。為了提高計算效率，更真實地模擬剛玉塊石混凝土復合遮彈層的組成和構造特性，本文中對三維隨機骨料生成算法和普通塊石遮彈層生成算法[7-8]進行改進。

(1)改進三維剛玉塊石生成算法。如圖1所示，在圓內接隨機四邊形生成算法中，引入內角控制參數i和邊長控制參數li(i=1,2,3,4)，避免薄片狀和尖角狀空間隨機八面體的產生，在此基礎上生成的三維隨機多面體，能夠更真實地模擬剛玉塊石顆粒。

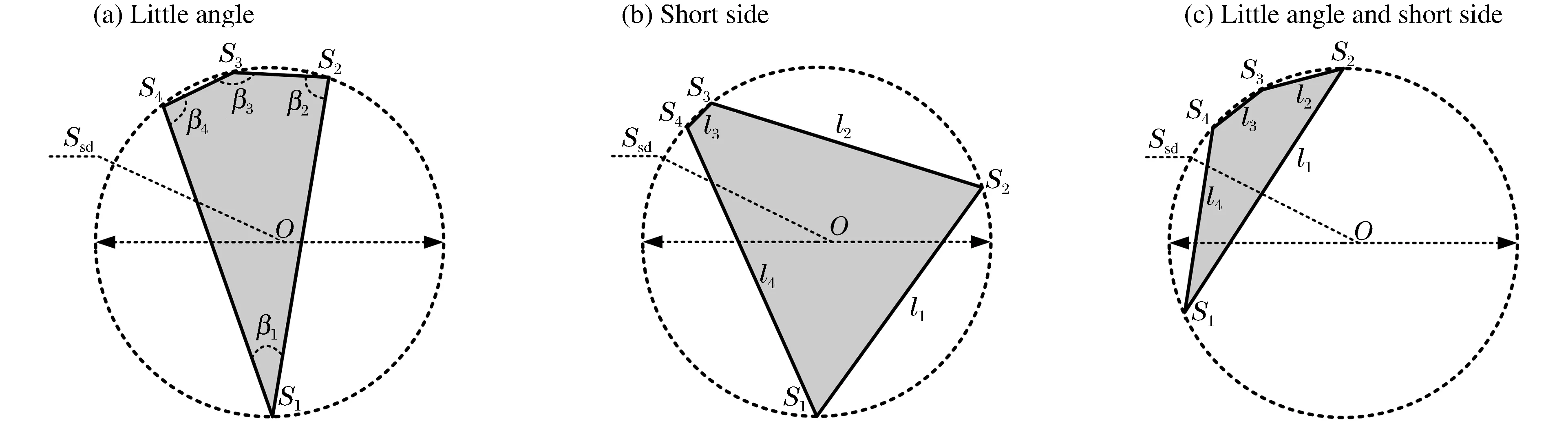
圖1 應避免的圓內接隨機四邊形Fig.1 Bad random quadrilateral inscribed

(2)優化三維隨機多面體空間投放算法。根據take & place投放算法基本流程，在每一個剛玉塊石顆粒投放過程中，引入投放次數控制參數，當某一待投放顆粒達到一定投放次數后，仍不滿足邊界條件和無重疊條件時，舍棄該顆粒，開始計算下一個顆粒的投放。投放次數控制參數對提高投放算法的效率，起到了很好的效果。

(3)綜合運用密實算法，提高剛玉塊石顆粒投放密度和投放效率。隨機投放模型生成后，為了進一步提高剛玉塊石的投放密度，本文中進一步提出密實算法。通過引入剛性塊體間接觸算法，分別采用重力自密實和模型底部施加正弦振動機械密實的方法，進一步提高剛玉塊石的投放密度和計算效率。

(4)優化網格剖分和材料屬性判定算法。為了提高網格剖分和材料屬性判定計算效率，節省建模時間，本文中提出了區域剖分判定算法。首先，將靶體模型劃分為Ωm個大的區域(m<100)，Ωi和Ωj(i≠j)容許有小部分重疊；其次，建立區域鏈表數組，存放各個區域內所包含的剛玉塊石顆粒；再次，在進行網格材料屬性計算時，Ωi域內的網格只需要與該域內包含的顆粒進行位置關系判定即可，大大縮短了每一個循環步的計算時間；最后，合并各個區域計算結果，清除重疊網格，輸出有限元模型。計算結果表明，本文中提出的剛玉塊石遮彈層模型生成算法，比文獻[7-8]的算法更可靠，且計算效率顯著提高。

1.2 有限元模型

圖2 彈體和剛玉塊石遮彈層有限元模型Fig.2 Finite element models for a projectile and a corundum-rubble target

本文中選用小直徑炸彈(small-diameter bomb, SDB)作為侵徹彈體，彈頭曲率半徑為3，彈體質量為113.4 kg，彈體長度為182.88 cm，彈體直徑為15.24 cm。建模時按照總質量相等原則,視彈體為均質實體，等效密度為3 862.5 kg/m3。有限元計算中，采用三維六面體單元進行網格剖分，共計8 000個單元。彈體的單元尺寸為1.8 cm，與靶體單元尺寸接近。

遮彈層靶體分為2層:上層為剛玉塊石混凝土層，下層為混凝土底座(取波阻抗與上層相同，目的是減小計算量)。上層尺寸取為150 cm×150 cm×250 cm，下層尺寸取為150 cm×150 cm×30 cm，有限元模型見圖2。在遮彈層四周設置透射邊界，吸收膨脹波和剪切波，上表面自由，底面固支。選用三維六面體單元，采用單點積分和沙漏控制以更好地描述大變形和材料失效等非線性問題。為了提高運算速度，減少單元的數目，同時保證計算精度，在對靶體進行有限元網格剖分時，在靶體中心2.5倍彈徑范圍內劃分較細，中心細化區域網格尺寸為1 cm，其他范圍的網格尺寸為2 cm。劃分后,遮彈層模型的實體單元為1 089 000個。

1.3 計算參數

SDB材料為4340鋼，計算時采用Johnson-Cook模型及Grüneisen狀態方程描述其力學性能[9-11]，材料參數見表1[11]。對靶體中填充的混凝土材料，采用Johnson-Holmquist-Concrete模型描述[12-13]，材料參數按文獻[12-14]選取，見表2。對剛玉塊石材料采用Johnson-Holmquist-Ceramic模型描述，材料參數見表3[15-16]。

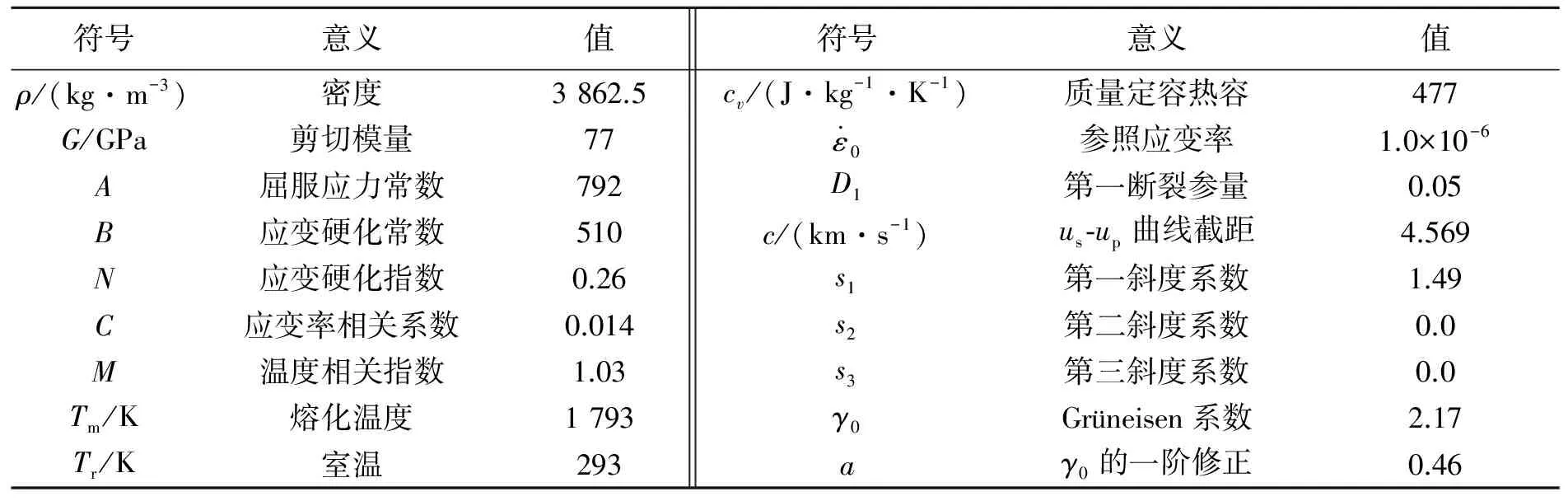
表1 小直徑炸彈材料的計算參數[11]

表2 混凝土材料的計算參數[12-14]

表3 剛玉塊石的計算參數[15-16]

2 計算結果及討論

數值模擬中，編號為No.0001的靶體為標準靶體，其參數取為：剛玉塊石-彈徑比Drk/D=1.5，填充混凝土為C30，剛玉塊石體積分數Vrk=50%。所有的計算工況如表4所示，其中考慮了不同侵徹位置、侵徹入射角α、撞擊速度v、剛玉塊石體積分數Vrk以及填充混凝土強度fc等對侵徹結果的影響。

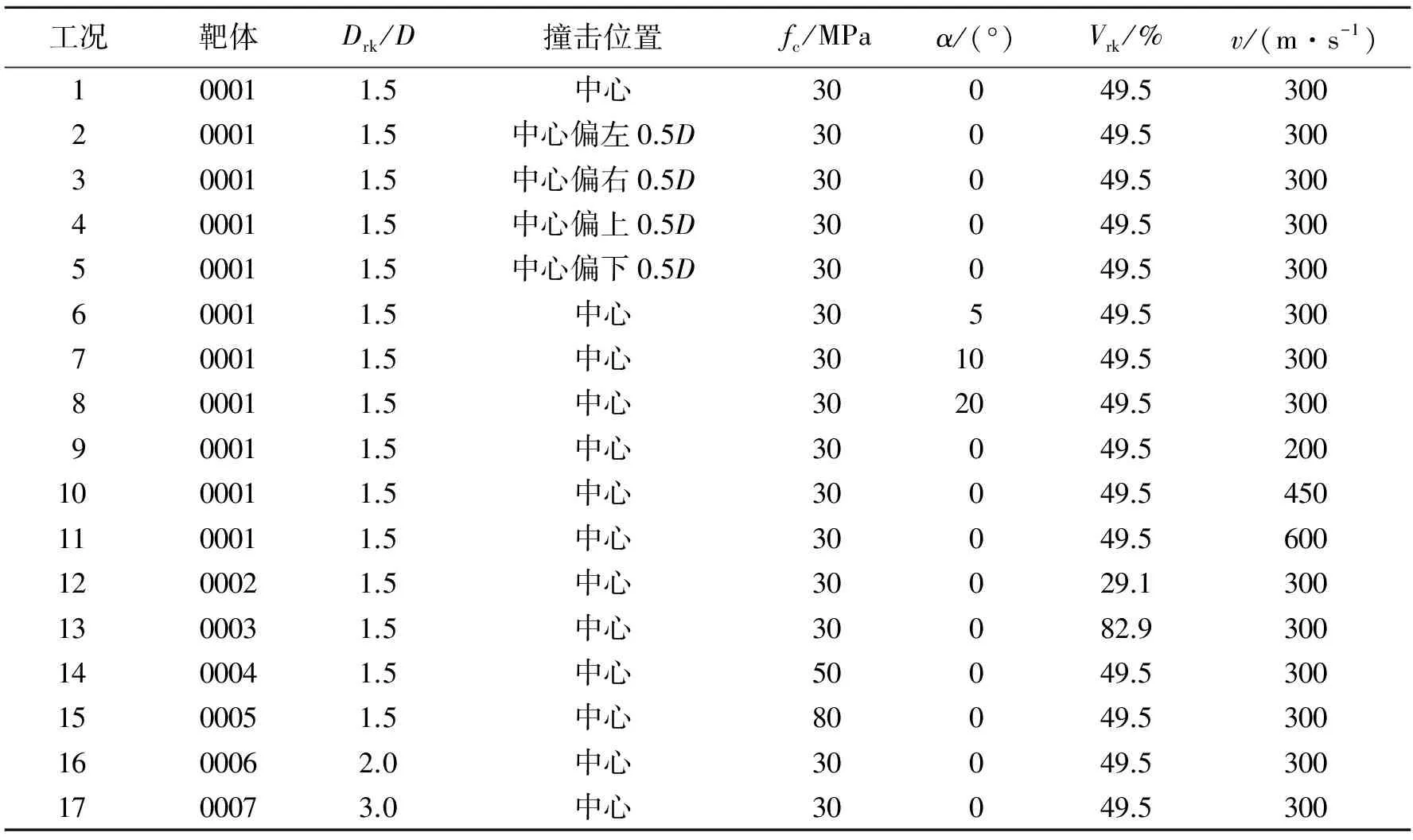
表4 計算工況

2.1 彈著點位置的影響

計算工況1～5中考慮了彈著點位置對侵徹結果的影響，計算結果見圖3。從圖3可以看出：與計算工況1相比，侵徹深度H和彈體偏轉角β的變化幅度分別為12%和35%。由此可見，不同的侵徹位置對計算結果有一定的影響，其主要原因是剛玉塊石的隨機不均勻分布所致。

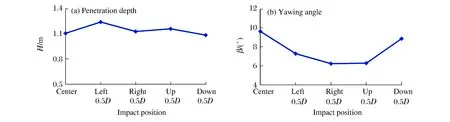
圖3 彈著點對侵徹結果的影響Fig.3 Effects of impact position on penetration

2.2 侵徹速度的影響

以下考慮彈體速度分別為200、300、450、600 m/s等4種情況下的計算結果，對應表4中工況1以及工況9～11，計算得到的侵徹深度和彈體偏轉角如圖4所示。

從圖4可以看出：侵徹速度為200～450 m/s時，侵徹速度與侵徹深度呈線性關系，偏轉角與侵徹速度也呈現相同變化的趨勢；侵徹速度大于450 m/s后，偏轉角的增加減緩。彈體的變形和終點彈道如圖5(a)所示。由此可見，剛玉塊石遮彈層對彈體的偏轉作用顯著，這大大減小了彈體的侵徹深度。

2.3 入射角的影響

不同入射角條件下的計算結果如圖6所示，對應表4中的計算工況1、6～8。從圖6可以看出:侵角從0°(正侵徹)增長到15°，侵徹深度由1.018 m減小到0.791 m，彈體偏轉角從9.63°增大到50.89°。彈體的變形和終點彈道的形狀如圖5(b)所示。由此可以看出，入射角對侵徹結果有較大的影響。

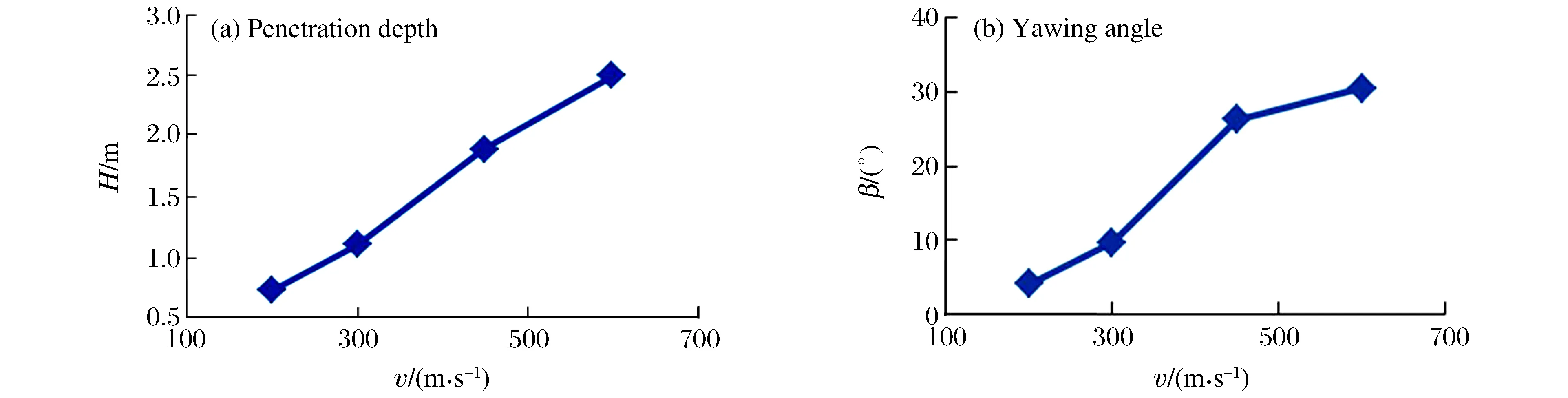
圖4 侵徹速度對侵徹效應的影響Fig.4 Effects of impact velocity on penetration

圖5 彈體撞擊速度和入射角對彈體變形和靶體終點彈道的影響(橫截面)Fig.5 Effects of impact velocity and impact obliquity on projectile deformation and trajectory (vertical section)

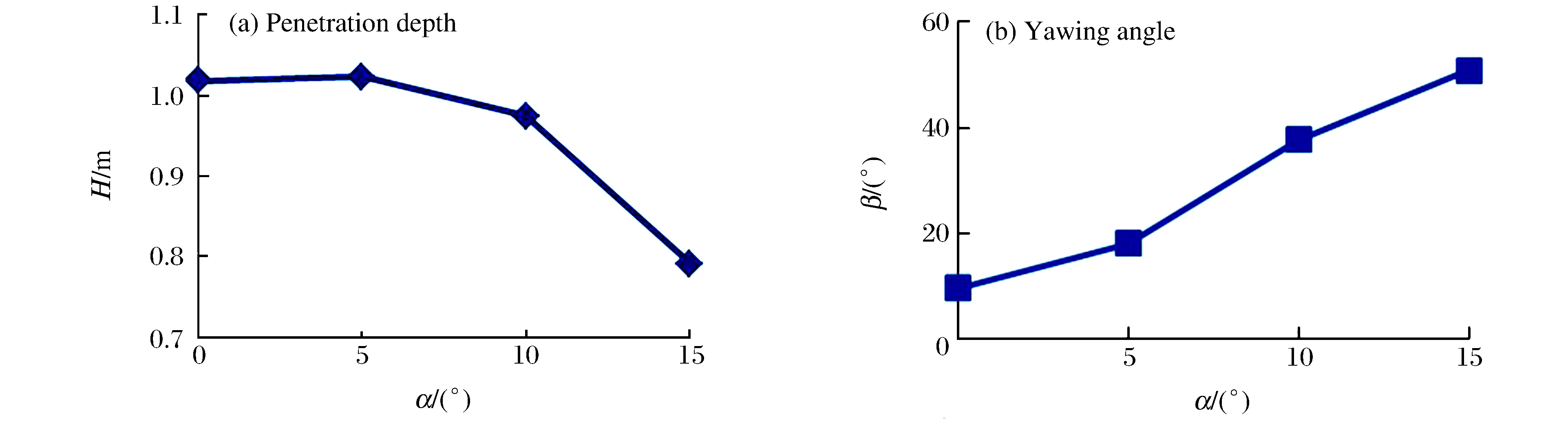
圖6 彈體入射角對侵徹效應的影響Fig.6 Effects of impact obliquity on penetration

2.4 剛玉塊石大小的影響

剛玉塊石大小對侵徹效應影響的計算結果如圖7所示，當剛玉塊石的大小從1.5D增加到3.0D時，侵徹深度從1.108 m減小到0.783 m，彈體侵徹偏轉角從9.63°增加到18.79°，由此可見，剛玉塊石的大小對彈體的侵徹深度和偏轉角都會產生較大影響。

2.5 與塊石混凝土遮彈層計算結果的對比

剛玉塊石與普通塊石相比，強度更高，硬度更大，是一種更好的抗侵徹材料。為進一步掌握剛玉塊石混凝土靶體的抗侵徹性能，本文中將剛玉塊石的計算結果與普通塊石混凝土遮彈層的計算結果[8]進行了對比，見圖8。從圖8可以看出：在侵徹速度為300 m/s、Drk/D=1.5的情況下，雖然彈體對剛玉塊石遮彈層和普通塊石遮彈層的侵徹深度都隨填充混凝土強度和塊石體積分數的增加而減小，但剛玉塊石混凝土遮彈層的抗侵徹能力是普通塊石混凝土遮彈層的2倍以上。

圖7 剛玉塊石大小對侵徹效應的影響Fig.7 Effects of corundum volume on penetration

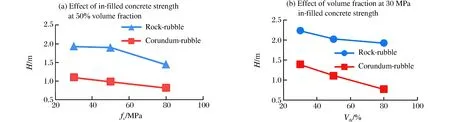
圖8 剛玉塊石與塊石遮彈層抗侵徹能力對比Fig.8 Comparison of penetration effect between rock-rubble and corundum-rubble overlays

3 結 論

(1)剛玉塊石的隨機分布特性對侵徹結果有一定的影響；(2)隨著彈體侵徹速度的增大，侵徹深度以及彈體偏轉角度隨之增大；(3)彈體侵徹角度的增加可減小侵徹深度，增大彈體偏轉角度；(4)剛玉塊石的大小對侵徹深度有較大影響，當剛玉塊石的直徑與彈徑比值Drk/D=1.0～1.5時，侵徹深度變化較小，但當Drk/D從1.5增加到3.0時，侵徹深度呈線性減小；(5)剛玉塊石遮彈層的侵徹深度隨填充混凝土強度和剛玉塊石體積分數的增加而減小；(6)剛玉塊石混凝土遮彈層的抗侵徹能力是普通塊石混凝土遮彈層抗侵徹能力的2倍以上。

[1] Austim C F, Halsey C C, Clodt R L. Protection systems development[R]. Tyndall Airforce Base: Report ESL-TR-83-39, 1982.

[2] Gelman M D, Richard B N, Ito Y M. Impact of armor-piercing projectile into array of large caliber boulders[R]. Waterways Experiment Station, 1987.

[3] Rohani B. Penetration of kinetic energy projectiles into rock-rubbles/boulder overlays[R]. Vicksburg, Mississippi: U.S. army Engineer Waterways Experiment Station, 1987.

[4] Langheim H, Pahl H, Schmolinske E, et al. Subscale penetration tests with bombs and advanced penetration against hardened structures[C]∥The Sixth International Symposium on Interaction of Nonnuclear Munitions with Structures. Panama City Beach, Florida, 1993:12-17.

[5] 唐德高,賀虎成,陳向欣,等.剛玉塊石混凝土抗彈丸侵徹效應試驗研究[J].振動與沖擊,2005,24(6):37-39. Tang De-gao, He Hu-cheng, Chen Xiang-xin, et al. Experimental study on corundum-rubble concrete against projectile[J]. Journal of Vibration and Shock, 2005,24(6):37-39.

[6] 唐耀振.剛玉冶煉工藝學[M].北京:國家機械委機床工具工業局,1987:8-10.

[7] 方秦,張錦華,陳力,等.全級配混凝土三維細觀模型的建模方法研究[J].工程力學,2013,30(1):14-21. Fang Qin, Zhang Jin-hua, Chen Li, et al. The investigation into three-dimensional mesoscale modelling of fully-graded concrete[J]. Engineering Mechanics, 2012,30(1):14-21.

[8] Fang Qin, Zhang Jin-hua. 3D numerical modeling of projectile penetration into rock-rubble overlays accounting for random distribution of rock-rubble[J]. International Journal of Impact Engineering, 2014,63:118-128.

[9] 黃民榮,高永宏,顧曉輝.剛性彈丸對花崗巖垂直侵徹的理論分析[J].南京理工大學學報:自然科學版,2008,32(6):724-728. Huang Min-rong, Gao Yong-hong, Gu Xiao-hui. Theoretical analysis for rigid projectiles normal penetration into granites[J]. Journal of Nanjing University of Science and Technology: Natural Science, 2008,32(6):724-728.

[10] 許瓊萍,王德榮,陸渝生.測定某種花崗巖靜摩擦系數的試驗[J].解放軍理工大學學報:自然科學版,2008,9(3):269-273. Xu Qiong-ping, Wang De-rong, Lu Yu-sheng. Experimental study on static friction coefficient of granite survey[J]. Journal of PLA University of Science and Technology: Natural Science Edition, 2008,9(3):269-273.

[11] 高文安.GB 50010-2010混凝土結構設計規范:鋼筋機械連接通用技術規程[S].北京:中國建筑工業出版社,2011:11-20.

[12] 王政,樓建鋒,勇珩,等.巖石、混凝土和土抗侵徹能力數值計算與分析[J].高壓物理學報,2010,24(3):175-180. Wang Zheng, Lou Jian-Feng, Yong Heng, et al. Numerical computation and analysis on anti-penetration capability of rock, concrete and soil[J]. Chinese Journal of High Pressure Physics, 2010,24(3):175-180.

[13] Holmquist T J, Johnson G R. A computational constitutive model for concrete subjected to large strains, high strain rates, and high pressures[C]∥14th International Symposium on Ballistics. Quebec, Canada, 1993.

[14] Beissel S R, Johnson G R.An abrasion algorithm for projectile mass loss during penetration[J]. International Journal of Impact Engineering, 2000,24(2):103-116.

[15] Mclntosh G. The Johnson-Holmquist ceramic model as used in LS-DYNA 2D: ADA357607[R]. Quebec Research and Development Branch Department of National Defence, 1998.

[16] Gazonas G A. Implementation of the Johnson-Holmquist Ⅱ (JH-2) constitutive model into DYNA3D[R]. ADA402347. Army Research Laboratory, 2001.

(責任編輯 張凌云)

Numerical analysis of the projectile penetration into the target of corundum-rubble concrete composite overlay

Fang Qin, Luo Man, Zhang Jin-hua, Sun Zhi-yuan

(PLAUniversityofScienceandTechnology,Nanjing210007,Jiangsu,China)

In order to investigate the performances of corundum-rubble overlays subjected to small-diameter bomb penetration, a three-dimensional finite element model is developed. The model is used to study the projectile penetration into the corundum-rubble overlay by taking into account the randomness of corundum-rubble in size, shape and spatial distribution. This paper focuses on the following two aspects. The first is the effects of penetration conditions (such as projectile velocity, impact angle and position) on penetration depth and terminal yawing angle. The second is the influences of the constituted parameters for the corundum-rubble overlay (such as size and volume fraction of corundum-rubble, strength of grouted concrete). The numerical results are compared with the data from rock-rubble overlay, and better performances are found for the corundum-rubble overlay subjected to projectile penetration.

mechanics of explosion; anti-penetration performance; three-dimensional model; corundum-rubble

10.11883/1001-1455(2015)04-0489-07

2014-02-21；

2014-06-08

國家自然科學基金項目(51321064,51108457,51378015)

方 秦(1962— )，男，博士，教授,博士生導師，fangqinjs@163.com。

O385;TJ012 國標學科代碼： 1303530

A