雙相介質半空間中圓孔對透射SH波的穩態分析

齊 輝，蔡立明，羅廣龍，潘向南，楊 杰，王憲章，李國文，蔣敬江

(1.哈爾濱工程大學航天與建筑工程學院，黑龍江 哈爾濱 150001； 2.上海電機學院機械學院，上海 201306； 3.中建一局總承包公司，北京 100070)

?

雙相介質半空間中圓孔對透射SH波的穩態分析

齊 輝1，蔡立明1，羅廣龍1，潘向南1，楊 杰2，王憲章3，李國文1，蔣敬江1

(1.哈爾濱工程大學航天與建筑工程學院，黑龍江 哈爾濱 150001； 2.上海電機學院機械學院，上海 201306； 3.中建一局總承包公司，北京 100070)

研究了平面SH波在半空間雙相彈性介質中的傳播。通過Green函數和積分方程方法，按照復變函數描述，對透射波被圓孔散射的情況進行穩態分析。將雙相介質半空間沿界面剖分為1/4空間介質Ⅰ和含圓孔的1/4空間介質Ⅱ，分別構造了介質Ⅰ和介質Ⅱ中反平面點源荷載的Green函數，按雙相介質中平面SH波的處理方法，給出介質Ⅰ和介質Ⅱ中的平面位移波，兩種介質之間的相互作用力與對應Green函數的乘積沿界面的積分與平面位移波疊加得到介質Ⅰ和介質Ⅱ中的全部位移場。按照界面的位移連續條件，定解積分方程組，得到問題的穩態解，并給出圓孔位置和介質參數對散射的影響。

固體力學；散射；Green函數；SH波；圓孔；雙相介質半空間；振動與波

彈性動力學中將研究對象視為連續的彈性體，運用數學物理的方法，解析地研究機械運動，不僅對數學物理的基礎科學研究具有重要意義，而且對巖土工程、地震工程等工程技術應用具有很大的價值。彈性波的傳播及其在全空間中被一些特殊曲面散射的研究已經日趨完善[1-4]。作為最簡單的波動模式，柱體在含復雜邊界介質中的反平面散射研究取得了一定的進展[5-6]。研究人員陸續研究了無限大彈性半空間、1/4空間中圓柱孔洞、夾雜、襯砌對SH平面波的穩態散射[7-12]。雙相介質半空間中SH波對圓柱孔洞、夾雜和界面裂紋的散射問題也得到了一定的研究[13-18]。這些研究中主要考慮入射波與孔洞或夾雜在同一介質內的散射問題，對于平面SH波從介質I穿過界面折射進入介質II，透射波對介質II中圓孔的散射問題的研究相對匱乏。本文中用Green函數和積分方程，按復變函數方法對其穩態響應進行分析，求解雙相介質半空間中位移場和應力場的解析表達式，并采用數值方法計算算例中圓孔邊沿動應力集中因子和地表位移幅值的分布。

1 理論模型

如圖1所示，連續、均勻、各向同性的彈性半空間，由介質Ⅰ和Ⅱ組成，其剪切模量分別為μ1和μ2，質量密度分別為ρ1和ρ2，兩種介質的分界為BV，這種雙相介質半空間的邊界平面為BH。介質Ⅱ中有一個圓形孔洞，其半徑為R，其圓心O1距離界面BV為d，距離邊界BH為h，定義平面直角坐標系O1x1y1(圖1)，以出平面方向為z軸正方向，x1軸、y1軸和z軸滿足右手關系。

在介質Ⅰ中有穩態SH平面波入射，其角頻率為ω。入射波與它在邊界BH上的反射和在界面BV的反射和透射，造成了介質Ⅰ與介質Ⅱ中質點的反平面運動，其反平面運動的位移分別為wⅠ和wⅡ，滿足標量波動方程：

(1)

分離時間變量和空間變量，得到對應的Helmholtz方程(介質Ⅰ和介質Ⅱ中位移場的控制方程)：

(2)

位移場wⅠ和wⅡ在半空間邊界BH平面上產生的剪應力都為0，滿足Neumann邊界條件；位移場wⅠ和對應的應力場τⅠ在界面BV上與位移場wⅡ和對應的應力場τⅡ相等，分別滿足Dirichlet邊界條件和Neumann邊界條件；應力場τⅡ在圓形孔洞邊界上為0，滿足Neumann邊界條件。這4個邊界條件與介質Ⅰ和介質Ⅱ中的控制方程(2)組成本文的定解問題。

2 等價問題

圖2 等價問題Fig.2 Equivalent issue

(3)

在介質Ⅰ中有一對穩態的SH平面波入射，其角頻率均為ω，初相位相等，入射角關于平面BH對稱，其位移wi1和wi2為：

(4)

這樣，本文中定解條件變成等價的邊值問題，由BV界面上位移和應力連續的Dirichlet和Neumann邊界條件，及介質Ⅱ中圓形孔洞邊界B1和B2柱面上剪應力自由的Neumann邊界條件組成。

介質Ⅰ中的入射位移波wi1和wi2在界面BV將發生反射和折射，折射波將透射進入介質Ⅱ，在圓形孔洞的邊界B1和B2柱面發生散射，散射波也將在界面BV發生反射和折射，為了分析界面BV對散射波的反射和折射效應，引入Green函數方法。

3 Green函數

按照Green函數方法，考慮點源荷載在界面BV上分別對介質Ⅰ和介質Ⅱ的穩態位移響應，其分離時間變量后，即為Green函數。

在介質Ⅰ中，點源荷載δ(z-iy0)exp(-iωt)產生的Green函數GⅠ(z,iy0)是半空間中的基本解，表達式為

(5)

圖3 介質Ⅱ中的Green函數Fig.3 Green function in medium Ⅱ

如圖3所示，在介質Ⅱ中，點源荷載δ(z-iy0)exp(-iωt)產生的Green函數GⅡ(z,iy0)，按照疊加原理，有：

(6)

(7)

(8)

介質Ⅱ對應半空間中的基本解G(z,iy0)，位移波wG1和w′G1的矢量和，位移波wG2和w′G2的矢量和，它們的應力場都滿足界面BV上的剪應力自由條件。位移場GⅡ(z,iy0)的應力場必須滿足圓形孔洞邊界B1和B2柱面上的剪應力自由條件做Fourier展開，得到等價的剪應力自由條件，用于確定Fourier-Hankel波函數系數An和Bn，即定解條件。根據三角函數系的正交性，得到和定解條件等價的兩組方程。截斷Fourier-Hankel波函數級數展開式，取對應的方程，組成定解方程組，按Gauss消去法解得An和Bn的具體數值，這樣，就確定了介質Ⅱ中Green函數GⅡ(z,iy0)位移場的具體表達式。

4 位移波場

圖4 位移波場的契合Fig.4 Conjunction of displacement wave field

介質Ⅰ中的位移場wⅠ(z)由3部分組成：入射波的位移場、反射波的位移場、介質Ⅱ對介質Ⅰ的作用力f(y)產生的位移場，其表達式為：

(9)

式中：wi1(z)和wi2(z)是入射波的位移場，根據式(4)，略去時間諧和項exp(-iωt)，得到入射波位移場的表達式：

(10)

wr1(z)和wr2(z)是反射波的位移場，表達式為：

(11)

介質Ⅱ中的位移場wⅡ(z)同樣由3部分組成：折射波的位移場、散射波的位移場，以及介質Ⅰ對介質Ⅱ的作用力-f(y)產生的位移場，表達式為：

(12)

wt1(z)和wt2(z)是折射波的位移場，表達式為：

(13)

式中：W2是折射波的振幅，β是折射波的角度(見圖4)。按照界面BV上位移和應力的連續性條件，角度α和β滿足Snell定律：

k1sinα=k2sinβ

(14)

入射波振幅W0、反射波振幅W1和折射波振幅W2，滿足

(15)

ws1(z)和ws2(z)是介質Ⅱ中圓形孔洞邊界B1和B2柱面對折射波的散射所產生的位移場，w′s1(z)和w′s2(z)是散射波ws1(z)和ws2(z)分別對界面BV反射產生的鏡像散射波的位移場，按照波函數展開法，得到：

(16)

5 積分方程

由(9)和(12)式，按照界面BV上位移和應力的連續條件，即契合條件，得到：

(17)

(18)

這是積分限為無窮的第一種Fredholm積分方程。在y軸上對界面BV取N+1個節點yk，同樣地，對積分區間取N+1個節點yl，按數值方法對(18)式進行離散求解：

(19)

式中：Ql是求積系數，伴隨求積節點yl，取決于數值積分所采用的方法。按Gauss消去法，計算節點yl上f(yl)的數值，之后用Lagrange插值擬合界面BV上的分布力f(y)

6 算例分析

按照第4節中的討論，結合第5部分求得的界面BV上的分布力f(y)，分別按照(9)式和(12)式，得到介質Ⅰ和介質Ⅱ中的位移場wⅠ(z)和wⅡ(z)，求得應力場τⅠ(z)和τⅡ(z)，它們足以描述介質Ⅰ和介質Ⅱ中全部質點的運動狀態。

(20)

(21)

為直觀的討論圓孔散射對水平邊界BH位移的影響，引入標準化的位移幅值W*(z)：

(22)

水平邊界BH平面的存在極大地影響了圓孔的散射，包括2部分：與圓孔到BH平面的距離h無關的鏡像透射位移波wt2(z)對圓孔的散射，以及隨著h的增大而衰減的鏡像散射波ws2(z)對圓孔的散射。水平邊界對圓孔散射的影響在彈性動力學反平面半空間問題中得到了廣泛的討論，相較而言，在雙相介質半空間中，垂直界面BV對介質Ⅱ中圓孔散射的作用更值得注意。

算例以圓孔半徑R為參考長度，給定h=2R，d=2R，取入射角α=0，數值計算雙相介質的不同波數、剪切模量對圓孔散射的具體影響，定義波數比k*=k1/k2，剪切模量比μ*=μ1/μ2。圖5和圖6分別給出由圓孔散射所造成的圓孔邊沿的動應力集中因子的分布和受其影響的水平邊界BH平面上標準化的位移幅值的分布。

圖5 動應力集中因子在圓孔邊沿的分布Fig.5 Distribution of dynamic stress concentrations factors around the cylindrical cavity

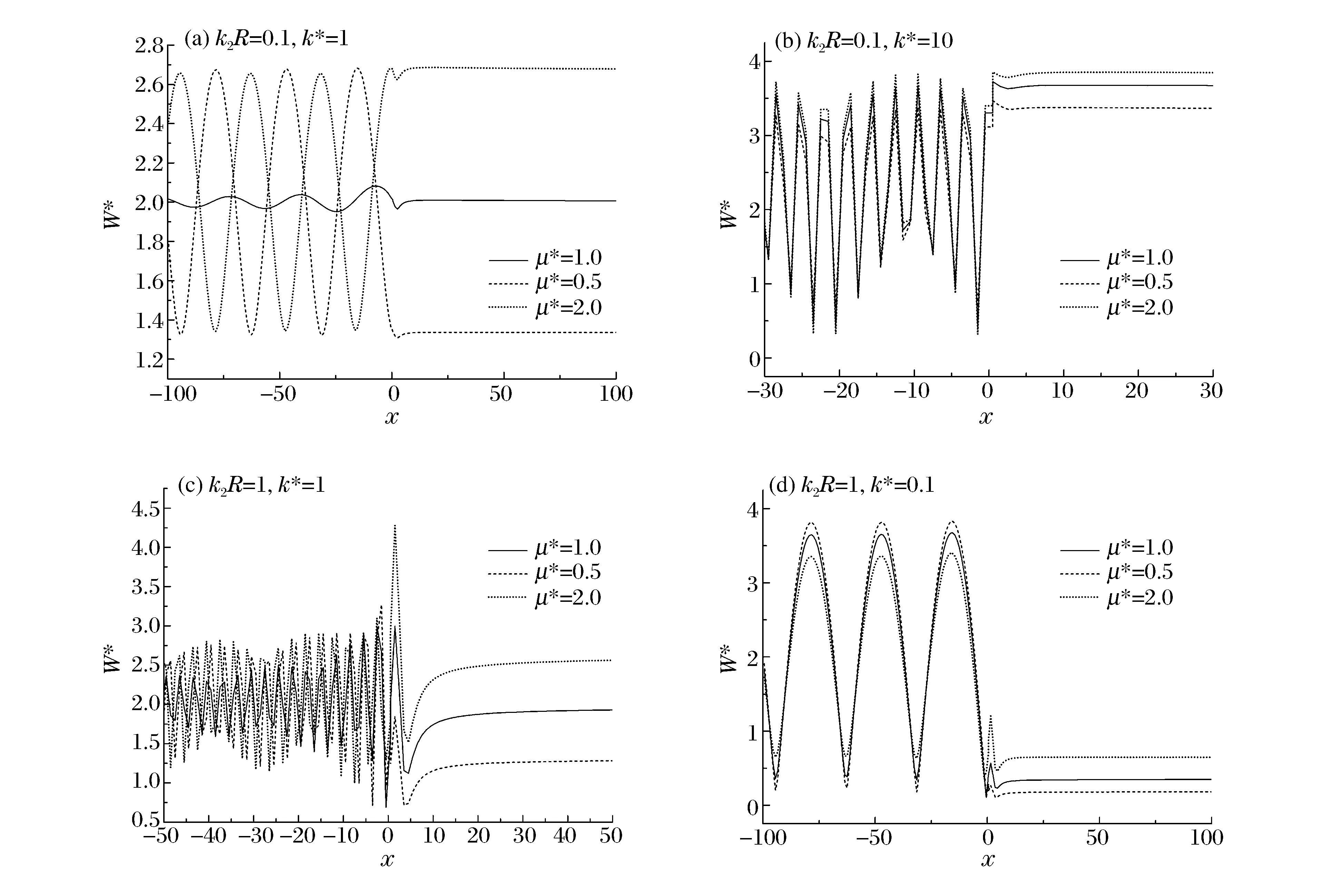
圖6 標準化位移幅值在水平邊界上的分布Fig.6 Distribution of normalized displacement amplitude along the horizontal bound

7 結 論

雙相介質半空間中圓孔的反平面穩態散射受到很多因素的影響，諸如，圓孔和邊界的距離、和界面的距離，雙相介質的波數比、剪切模量比，平面SH波的入射角度、頻率，等等。不同的圓孔位置對散射的影響可以參照1/4空間圓孔問題的研究，當圓孔距離界面足夠遠，界面另一側介質的影響可以忽略，界面附近的圓孔，對穿過界面的透射平面SH波的散射受到界面另一側介質的強烈影響，集中體現在介質的波數和剪切模量。作為SH波在雙相介質中傳播的問題，應充分考慮界面兩側介質對平面SH波透射的影響，給定入射角度和頻率。

在相對低頻的透射波作用下，圓孔散射造成更大的動應力集中，在相對高頻的透射波作用下，圓孔散射造成的動應力分布受到界面另一側介質的影響更大。在一定范圍內，界面另一側介質的剪切模量很大程度地決定著圓孔散射所造成的動應力的數值與分布，這種效應隨著界面另一側介質的質量密度的增大而減小。在相對高頻的透射波作用下，圓孔散射造成局部更大的地表位移，也更受界面另一側介質的影響，隨著界面另一側介質波數的增大，圓孔散射所造成的局部地表位移的變化也越大，這種效應隨著界面另一側介質的剪切模量的增大也略微地增大。

[1] Achenbach J D. Wave propagation in elastic solids[M]. Netherlands, Amsterdam: North-Holland, 1973.

[2] 胡德綏.彈性波動力學[M].北京:地質出版社,1989.

[3] Ying C F, Truell R. Scattering of plane longitudinal wave by a spherical obstacle in an isotropically elastic solid[J]. Journal of Applied Physics, 1956,27(9):1086-1097.

[4] PaoY H, Mow C C. Diffraction of elastic waves and dynamic wtress concentrations[M]. New York: Crane & Russak, 1973.

[5] Liu D K, Gai B Z, Tao G Y. Applications of the method of complex functions to dynamic stress concentrations[J]. Wave Motion, 1982,4(3):293-304.

[6] 劉殿魁.各向異性介質中Ⅲ型裂縫的動力分析[J].地震工程與工程振動,1991,11(2):29-38. Liu Dian-kui. Analysis of dynamic stresses of mode Ⅲ crack in anisotropic materials[J]. Earthquake Engineering and Engineering Vibration, 1991,11(2):29-38.

[7] 劉殿魁,劉宏偉.SH波散射與界面圓孔附近的動應力集中[J].力學學報,1998,30(5):597-604. Liu Dian-kui, Liu Hong-wei. Scattering and dynamic stress concentration of SH-wave by interface circular hole[J]. Acta Mechanica Sinica, 1998,30(5):598-604.

[8] 劉殿魁,田家勇.SH波對界面圓柱形彈性夾雜散射及動應力集中[J].爆炸與沖擊,1999,19(2):115-122. Liu Dian-kui, Tian Jia-yong. Scattering and dynamic stress concentration of SH-wave by interface cylindrical elastic inclusion[J]. Explosion and Shock Waves, 1999,19(2):115-122.

[9] 史文譜,劉殿魁,宋永濤.直角平面區域內固定圓形剛性夾雜問題的Green函數解[J].固體力學學報,2006,27(2):207-212. Shi Wen-pu, Liu Dian-kui, Song Yong-tao. The anti-plane Green function solution of the problem of a fixed rigid circular inclusion in right-angle plane[J]. Acta Mechanica Solida Sinica, 2006,27(2):207-212.

[10] 史文譜,劉殿魁,宋永濤,等.直角平面內圓孔對穩態SH波的散射[J].應用數學和力學,2006,27(12):1619-1626. Shi Wen-pu, Liu Dian-kui, Song Yong-tao, et al. Scattering of circular cavity in right-angle plane space to steady SH-wave[J]. Applied Mathematics and Mechanics, 2006,27(12):1619-1626.

[11] 折勇,齊輝,楊在林.SH波對直角平面區域內圓形孔洞的散射與地震動[J].應用力學學報,2008,25(3):392-397. Shi Yong, Qi Hui, Yang Zai-lin. Scattering of SH-wave by circular cavity in right-angle plane and seismic ground motion[J]. Chinese Journal of Applied Mechanics, 2008,25(3):392-397.

[12] 張根昌,齊輝,劉平安.SH波對直角平面區域內圓形襯砌的散射與地震動[J].力學與實踐,2013,35(1):60-66. Zhang Gen-chang, Qi Hui, Liu Ping-an. Scattering of SH-wave by circular lining in right-angle plane and seismic ground motion[J]. Mechanics in Engineering, 2013,35(1):60-66.

[13] 劉殿魁,林宏.SH波對雙相介質界面附近圓形孔洞的散射[J].固體力學學報,2003,24(2):197-2004. Liu Dian-kui, Lin Hong. Scattering of SH-waves by circular cavities near bi-material interface[J]. Acta Mechanica Solida Sinica, 2003,24(2):197-2004.

[14] 齊輝,折勇,李宏亮,等.SH波入射時垂直半空間中雙相介質界面附近圓孔的動力分析[J].爆炸與沖擊,2009,29(1):73-79. Qi Hui, Shi Yong, Li Hong-liang, et al. Dynamic analysis for scattering of SH-wave by circular cavities near bimaterial interfaces in a vertical half-space[J]. Explosion and Shock Waves, 2009,29(1):73-79.

[15] 齊輝,楊杰.SH波入射雙相介質半空間淺埋任意位置圓形夾雜的動力分析[J].工程力學,2012,29(7):320-327. Qi Hui, Yang Jie. Dynamic analysis for shallowly buried circular inclusions of arbitrary positions impacted by SH-wave in bi-material half space[J]. Engineering Mechanics, 2012,29(7):320-327.

[16] Qi H, Yang J, Shi Y. Scattering of SH-wave by cylindrical inclusion near interface in bi-material half space[J]. Journal of Mechanics, 2011,27(1):37-45.

[17] Qi H, Yang J, Shi Y, Tian J Y. Dynamic analysis for circular inclusion near interfacial crack impacted by SH wave in half space[J]. Journal of Mechanics, 2012,28(1):143-151.

[18] Qi H, Yang J. Dynamic analysis for circular inclusions of arbitrary positions near interfacial crack impacted by SH-wave in half-space[J]. European Journal of Mechanics: A: Solids, 2012,36:18-24.

(責任編輯 王小飛)

Steady state analysis for circular cavity impacted by transmitted SH wave in a bi-material half space

Qi Hui1, Cai Li-ming1, Luo Guang-long1, Pan Xiang-nan1, Yang Jie2, Wang Xian-zhang3, Li Guo-wen1, Jiang Jing-jiang1

(1.CollegeofAerospaceandCivilEngineering,HarbinEngineeringUniversity,Harbin150001,Heilongjiang,China; 2.SchoolofMechanicalEngineering,ShanghaiDianjiUniversity,Shanghai201306,China3.ChinaConstructionFirstEngineeringDivisionCorp.Ltd.,Beijing100070,China)

To study the way that the plane SH wave propagating in an elastic bi-material half space from medium Ⅰ to medium Ⅱ, the steady-state scattering of the transmitted wave by a circular cavity is analyzed by using Green function and integral equation methods on complex function description. The bi-material half space is divided into a quarter space medium Ⅰ and a quarter space medium Ⅱ with a circular cavity in it. Their Green functions are constructed as anti-plane point source response problem respectively. The total displacement fields of medium Ⅰ and medium Ⅱ are formulated as two parts’ vector sum. The first part is interfacial integral of interactive force multiplied by corresponding Green function. The second part is plane displacement field formed by omitting the circular cavity. Steady state solution is obtained by determining the integral equations along interface with displacement continuity. Numerical results are presented to reveal the effects of locations and material parameters on circular cavity scattering.

solid mechanics; scattering; Green function; SH wave; a circular cavity; a bi-material half space; vibration and wave

10.11883/1001-1455(2015)04-0591-08

2013-12-04；

2014-03-01

國家自然科學基金項目(51379048)

齊 輝(1963- )，男，博士，教授； 通訊作者： 潘向南，panxiangnan@hrbeu.edu.cn。

O343 國標學科代碼： 13015

A