MIMO 干擾信道中一種新的分布式迭代預編碼算法

高 磊，解培中

GAO Lei,JIE Peizhong

南京郵電大學 通信與信息工程學院，南京210003

College of Telecommunications& Information Engineering,Nanjing University of Posts and Telecommunications,Nanjing 210003,China

1 引言

多輸入多輸出（Multiple Input Multiple Output，MIMO）技術因其能極大提高無線通信系統容量而成為未來通信的關鍵技術之一[1]。然而在多用戶的通信系統中，多用戶使用同一頻帶通信，會在用戶的接收端造成共信道干擾（Co-channel Interference，CCI）。當基站通過互易或者反饋獲得CSI 信息時，通過協作多個共信道中相互干擾的發射器，可以抑制共信道干擾，從而達到提高和速率的目的[2]，這也就是預編碼技術。

經典的預編碼算法如迫零算法[3]和塊對角化算法[4]能完全消除共信道干擾，但缺點在于基站的發射天線數不得小于各空間復用用戶接收天線之和，這不符合現代通信的要求。為解決這一問題，研究者們開辟了新的研究方向。文[5]指出博弈論是無線網絡中分析資源沖突最合適的方法，并指出兩用戶干擾條件下（MISO-IC）信道的納什均衡解是兩個極限解，文[2]將信道擴展到MIMO條件下，并給出了分布式信道優化波束成形解。文獻[6]分析了基于信道反轉的BD 算法與基于SVD 分解的算法之間的聯系，并提出了適用于MIMO 廣播信道條件下的預編碼設計。另一個研究的熱點是干擾對齊，干擾對齊是將期望信號與干擾信號約束到各自子空間的方法，文獻[7]根據干擾對齊的概念，在三個用戶的構架下利用全局搜索和最小弦距離的方法設計預編碼，接收端濾波器則用迫零法設計，這樣就不可避免有上述迫零法的缺點。文獻[8-11]運用子空間的思想，通過分布式迭代泄漏的干擾功率量或信號空間距離使得期望信號空間與干擾信號空間的距離最大來實現算法的設計，需要特別指出的是文[10]中算法迭代的目標函數是信號功率和干擾功率的組合，兩者的組合系數依托于經驗值，信道的時變性為算法實現帶來很大挑戰。文獻[12]是在文[11]的基礎上引入了格拉斯曼流型的思想來尋找迭代的最快的下降方向，但算法中對步長的選擇較為苛刻。文獻[13]中提出了基于最小均方誤差準則的算法，在天線數目較多的時候，拉格朗日乘子的計算量大幅增加。文獻[14]綜合了文[8]和[13]的想法，通過最小噪聲泄漏的方法求得發送端預編碼，并根據最小均方誤差準則設計接收端的濾波器。除此之外，文獻[15]根據矩陣擾動理論，在慢衰落信道情況下，將波束跟蹤思想引入干擾對齊算法設計中，然而該設計方法并不適用于信道快速變化的情況。

本文主要研究多用戶MIMO 干擾信道下行鏈路的預編碼設計，假設一個中心單元已知全部的CSI，即預編碼和接收濾波矩陣是在已知基站和用戶之間所有CSI 的情況下協作運算獲得，這是一種分布式的思想。文中將多數據流的預編碼矩陣設計轉換成單數據流的預編碼矢量設計[16]，受文獻[2]啟發本文根據虛擬信干噪比和實際信干噪比最大原則（為了和虛擬信干噪比這個概念相對應，文中將通常所說的接收端接收信號的信干噪比稱為實際信干噪比，這樣第3 章所提算法可稱為最大虛實信干噪比迭代算法），提出了MIMO 干擾信道下分布式預編碼算法。此外，在最大虛擬信噪比和最小均方誤差的條件下給出了另一種迭代算法。

全文中，黑斜體小寫字母表示向量，黑斜體大寫字母表示矩陣，I表示是單位陣，C表示復數域，E(·)表示期望，‖A‖ 表示求矩陣A的F范數，AH表示A的共軛轉置，Vmax{A}表示A的最大特征值所對應的特征向量。

2 系統模型

文中使用的K用戶MIMO 干擾信道下行鏈路模型如圖1 所示。

設有K個發送接收對，每個發射機對應一個接收機，第l個發射機配置Nl根天線，第l個接收機配置Ml根天線，為簡化分析，設M1=Ml=…=M，N1=Nl=…=N。發射機k發送的數據流表示為sk，一次發送數據流為dk，則，其中dk≤min(M，N)。

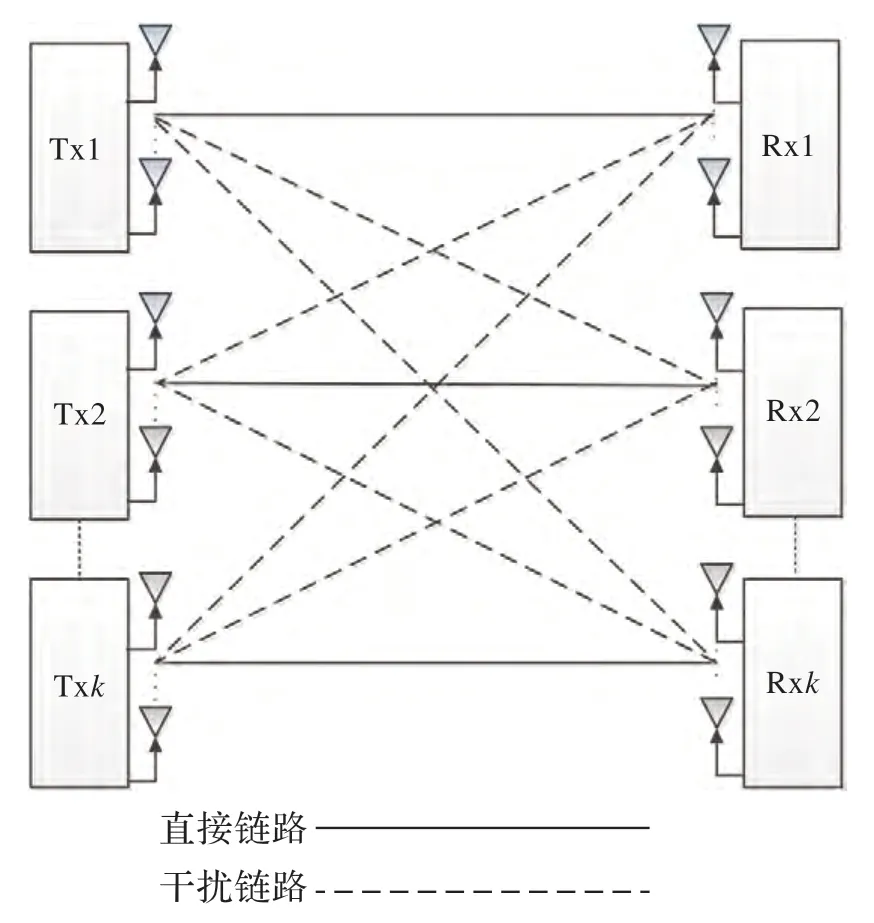
圖1 三用戶MIMO 干擾信道

發射機k先用線性預編碼器，將符號sk映射到N根發送天線上，則有：

然后將維數為N×1 的矢量xk廣播到信道中。

本文考慮窄帶MIMO 干擾信道，每條通信鏈路在發送數據期間是靜態的，但數據成功發送后可以改變，即塊衰落模型，假設系統中所有發射機同步發送且通信網絡中無頻率偏移。式（1）中sk是獨立同分布的且滿足，預編碼矩陣滿足，為簡化分析，設發送功率P1=Pk=…=P，數據流d1=dk=…=d，則接收端k所接收到的信號為：

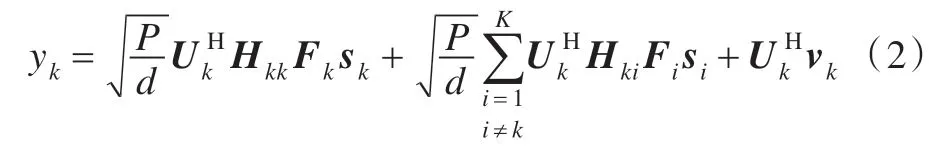
式中Hki∈CM×N發射機i到接收機k之間的信道矩陣，本文假設信道為瑞利衰落分布，Hki中元素是零均值、方差為1 的獨立同分布復高斯變量。vk是均值為零方差為的復加性高斯白噪聲，滿足。Uk∈CM×d表示接收端k的接收濾波矩陣滿足。式中第一項表示期望信號，第二項為用戶間干擾信號，第三項為噪聲信號。

將多數據流轉換為單數據流，從數學角度來看，式（1）可以改寫為：

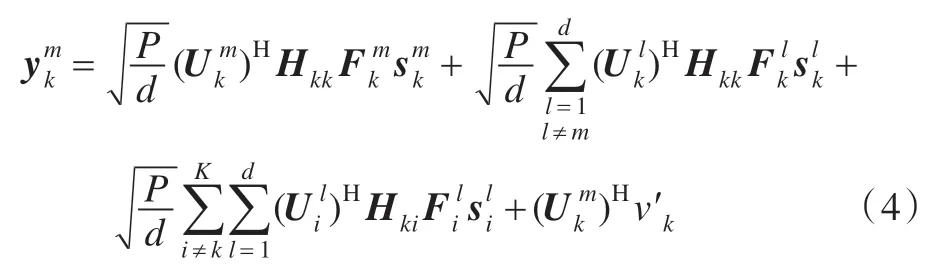
3 算法設計

3.1 最大虛擬信干噪比和實際信干噪比的迭代算法

干擾對齊這一技術的出現為現代通信中的干擾管理提供了新的思路，滿足干擾對齊的預編碼矩陣和接收濾波器需要滿足式（5）～（6）的條件[16]：

然而現有干擾對齊的算法大多都專注于信號空間的對齊（即將期望信號和干擾信號盡可能地約束到各自的子空間）和尋找更多維數的抗干擾子空間[16]，而對于如何使得期望信號子空間內的期望信號功率最大，并沒有做過多的研究和嘗試。本文考慮一種干擾對齊算法的自然擴展，優化的目標從最小噪聲泄漏轉變為信干噪比最大，文獻[16]中給出一種最大信干噪比算法，但是該算法要求信道互易，這使得算法應用有一定的局限性，下面介紹本文的方法。

根據式（4）可得到接收機k接收到目標發射機發送的第m個數據流的信干噪比為：

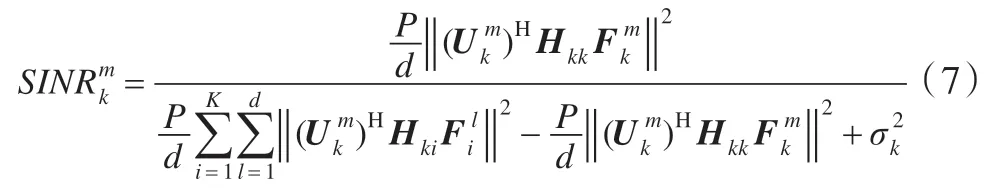
上式給出了接收端實際信干噪比表達式，其中分子表示接收端接收到的期望鏈路的信號功率，分母表示其他通信鏈路對期望鏈路的干擾功率之和，下面給出虛擬信干噪比的概念，仿照式（7）在發送端定義一個虛擬的信干噪比，即分子為期望鏈路信號功率不變，而分母變為發射機k發送的信號對其他通信鏈路的干擾功率之和，那么發射機k發射第m個數據流時的虛擬信干噪比可表示為：

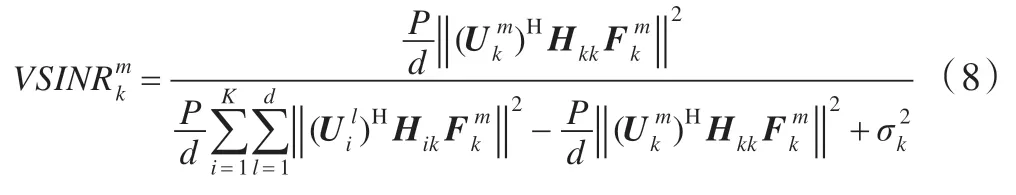
當場景為噪聲受限時式（8）退化為信干比SIR，當場景為干擾受限時式（8）退化為SNR。虛擬信干噪比可以近似看作系統的上行鏈路，即基站k用處理接收信號時的SINR；從另一角度來看，發射機發送的信號在目標接收端被視為有用的信號接收，在其他接收端被視為無用的干擾濾除，如此虛擬信干噪比亦在某種程度上近似地反映了基站發送的信號功率在整個網絡中的利用率。在實際優化中希望干擾噪聲功率盡可能小，期望信號功率盡可能大，即發送端預編碼向量要使式（8）最大：

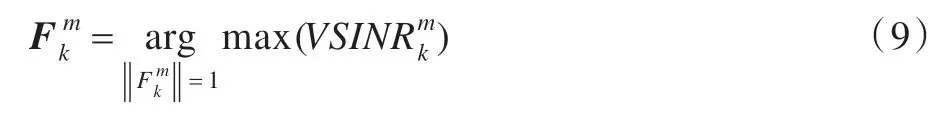
求式（9）可得發射機k第m個數據流對應的預編碼向量為式（10）。

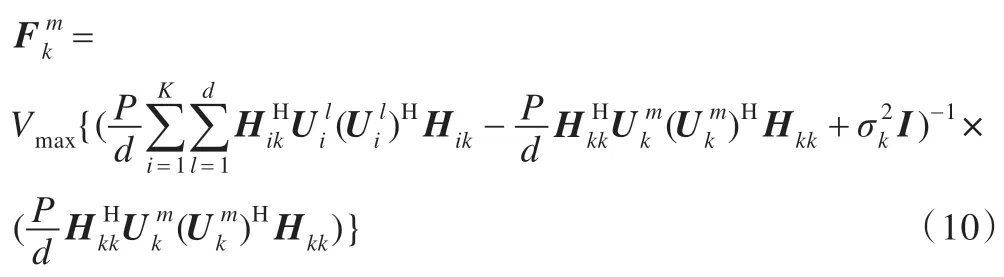
證明式（8）可以改寫為式（11），觀察式（11）可知這是個求解廣義瑞利商的問題，則式（10）得證。

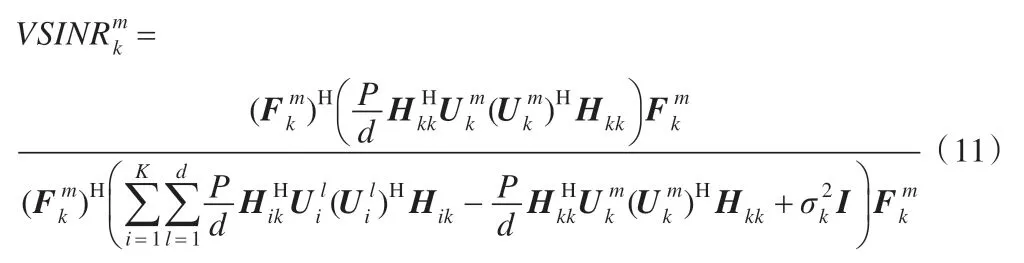
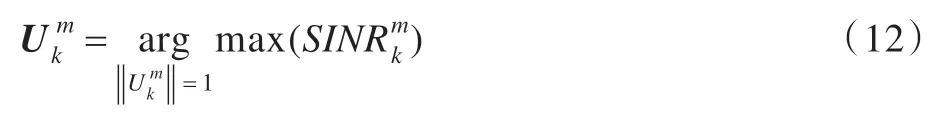
同理可以得到接收機k接收到的信號的第m個數據流對應的濾波向量為式（13）。

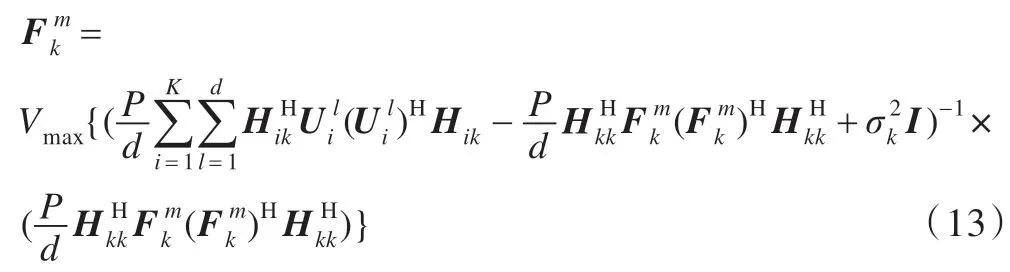
算法迭代步驟如下：

最大虛實信干噪比迭代算法

1.初始化接收濾波矩陣Uk∈CM×d，Uk的列向量是線性獨立同分布的單位向量。

2.根據式（10）以及步驟1 中的Uk求得發送端k第m個數據流的預編碼向量，并對所得的進行施密特正交化，?k∈{1，2，…，K}，?m∈{1，2，…，d}。

4.重復步驟2～3，直至迭代結束。

5.輸出Fk，Uk，?k∈{1，2，…，K}。

3.2 虛擬信干噪比和MMSE 混合迭代算法

由虛擬信干噪比的定義式（8）可知，虛擬信干噪比可視作發送信號在目標接收端的利用率，通過使發送信號在目標接收端的利用率最大，就相對地減少了對其他接收端的干擾，實現對噪聲的抑制。在接收端使用MMSE 算法可使接收信號誤差最小，通過兩者的迭代可以有效地實現對干擾的抑制，文獻[14]中所述的算法亦是利用該方法，通過最小噪聲泄漏和MMSE 混合迭代以實現算法設計。

利用以上思想，本章用虛擬信干噪比最大的方法獲得預編碼，同時滿足接收端接收信號與期望信號之間均方誤差最小的可表示為：

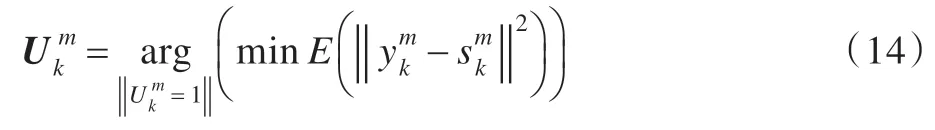
由式（13）得

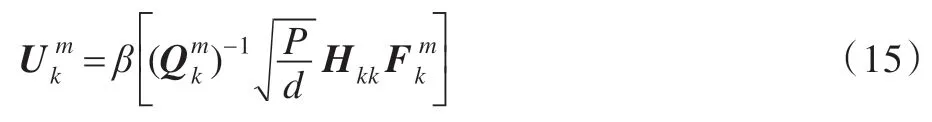
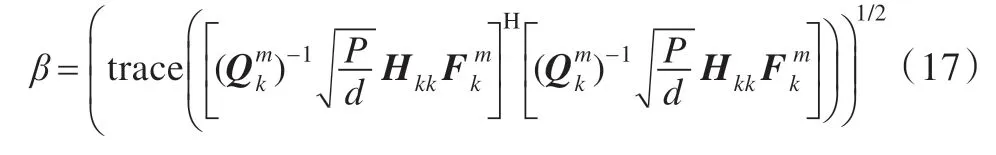
算法迭代步驟如下：

虛擬信干噪比和MMSE 混合算法

1.初始化接收濾波矩陣Uk∈CM×d，Uk的列向量是線性獨立同分布的單位向量。

2.根據式（10）以及步驟1 中的Uk求得發送端k第m個數據流的預編碼向量，并對所得的Fk進行施密特正交化，?k∈{1，2，…，K}，m∈{1，2，…，d}。

4.重復步驟2～3，直至迭代結束。

5.輸出Fk，Uk，?k∈{1，2，…，K}。

3.3 算法復雜度和收斂性分析

根據兩種算法的推導，相同情況下虛擬信干噪比和MMSE 混合算法的復雜度比最大虛實信干噪比算法低一些，因為它避免了求解矩陣特征值的運算。與文獻[8]中經典的最優子空間算法相比，當天線數M=N、發送數據流d=1 時，最大虛實信干噪比算法在每次迭代中比子空間最優算多4 次矩陣相乘運算和一次矩陣求逆運算對應的復雜度分別為3?O(N3)+O(N2)和O(N3)，由下一章節仿真結果部分可知，算法收斂所需迭代次數與最優子空間算法相近，和速率性能較后者有大幅度的提高。當數據流數大于1 時，提出的兩種算法較之其他算法性能仍有較大的提升，但是其復雜度也會隨之提高。

文中算法的優化目標函數為信干噪比，在使分子盡可能大的同時希望分子盡可能的小，該情況下很難用理論方法證明算法的收斂性，本文參照了文獻[14]中說明算法收斂性的方法，通過仿真得出算法的和速率隨迭代次數的增加而趨于穩定，出現了平臺效應，由此可以說明算法是收斂的。

4 仿真

本章對所提出的算法進行仿真分析，所有的仿真結果都是在每個信道為獨立同分布方差為1 的復高斯系數前提下評估期望和速率。為了給算法性能提供一個統一的衡量標準以方便性能的比較，文章中沿用文獻[8]和速率的公式如式（18）：

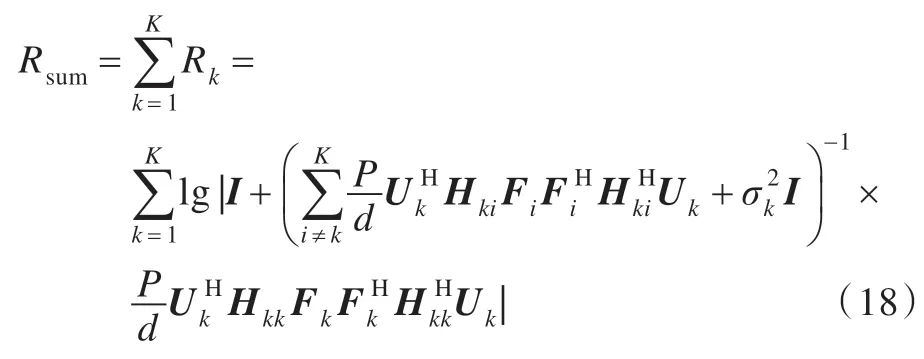
圖2 顯示的是最大虛實信干噪比迭代法、虛擬信干噪比與MMSE混合法與子空間最優算法[8]、AMIA算法[11]以及最小干擾泄漏和MMSE 混合算法[14]的和速率隨信噪比變化趨勢，為公平起見，圖中迭代算法的迭代次數均為100 次，使用MIMO 信道模型為[4×4，1]3，其中4×4表示M×N=4×4，1 表示發送數據流d=1，上標3 表示三個用戶。由圖2 可知d=1 時，文中的兩種算法的和速率性能相接近且較之最小干擾泄漏MMSE 混合算法、子空間最優算法以及AMIA 算法有很大幅度的提高，同時由文[13]、[14]可知最小干擾泄漏和MMSE 混合算法性能優于文[13]中給出的最小均方誤差迭代算法。故而文中的算法性能亦優于文[13]中的最小均方誤差迭代算法。圖3 顯示的是發送多數據流時的性能曲線，即[6×6，3]3信道模型下，上述幾種算法的和速率隨信噪比變化曲線圖，從圖中可以看出，各算法曲線的相對位置與圖2 基不變。

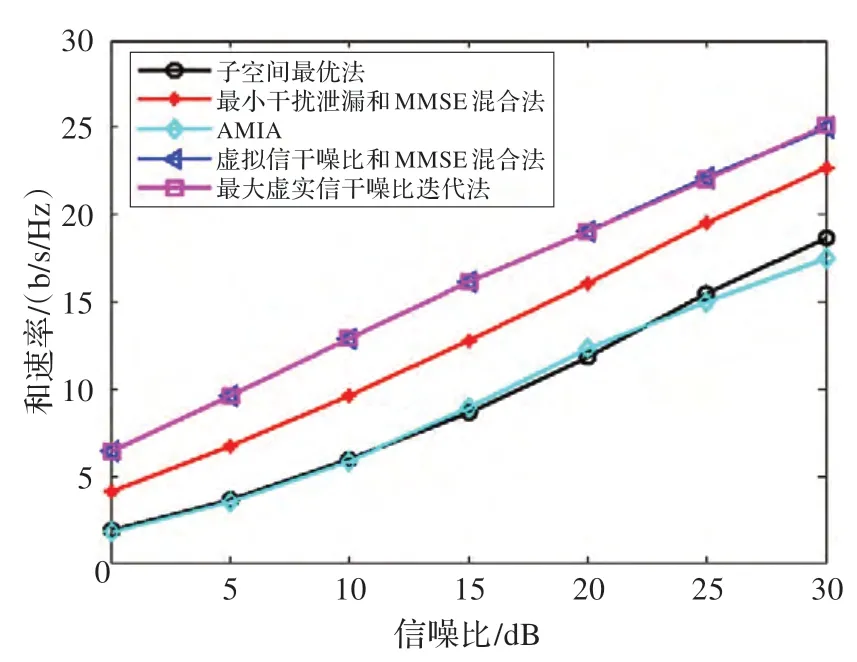
圖2 [4×4，1]3 情況下和速率與信噪比的關系

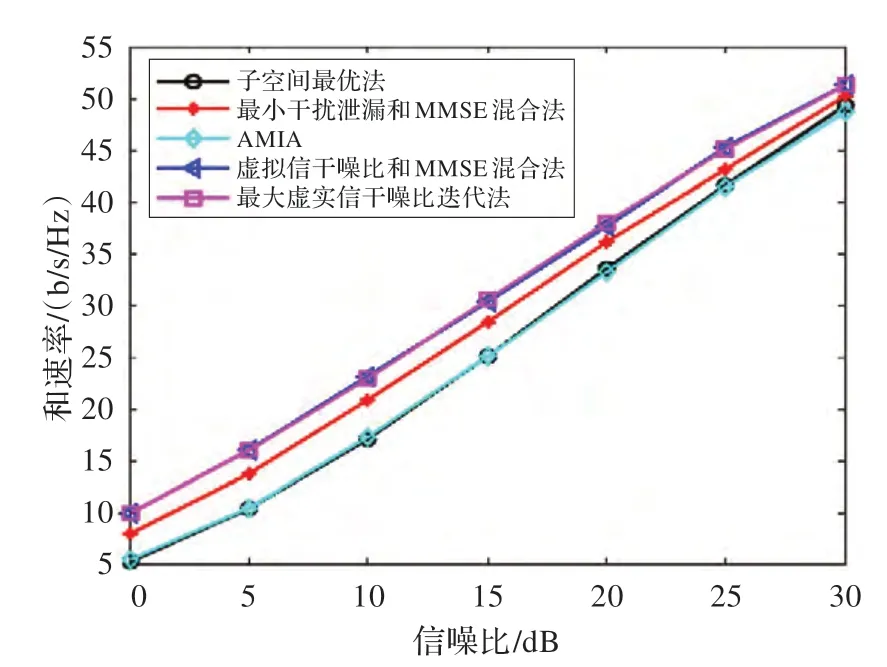
圖3 [6×6，3]3 情況下和速率與信噪比的關系

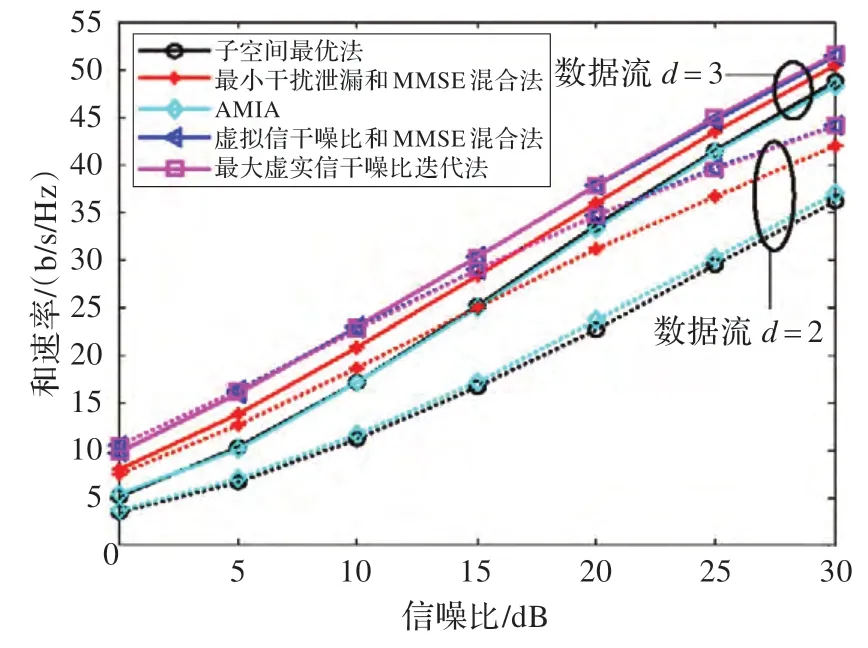
圖4 [6×6，2/3]3 時和速率與信噪比的關系

圖4 顯示的是測試三用戶M×N=6×6 條件下，上述各種算法的和速率隨信噪比變化曲線圖，不同的在于本次測試對發送不同數據流的情況進行了比較，圖中虛線的發送數據流d=2，實線的發送數據流d=3，數值仿真曲線表明，在發送數據流d=2 的情況下，本文提出的算法性能較之其他算法有很明顯的提升，提升的幅度大于發送數據流d=3 時的情況。多次數值仿真測試表明：測試環境相同時，同一種算法在發送數據流不大于算法自由度[17]的條件下，發送數據流數越多，和速率就越大，文中算法性能較之其他算法提升幅度越小。

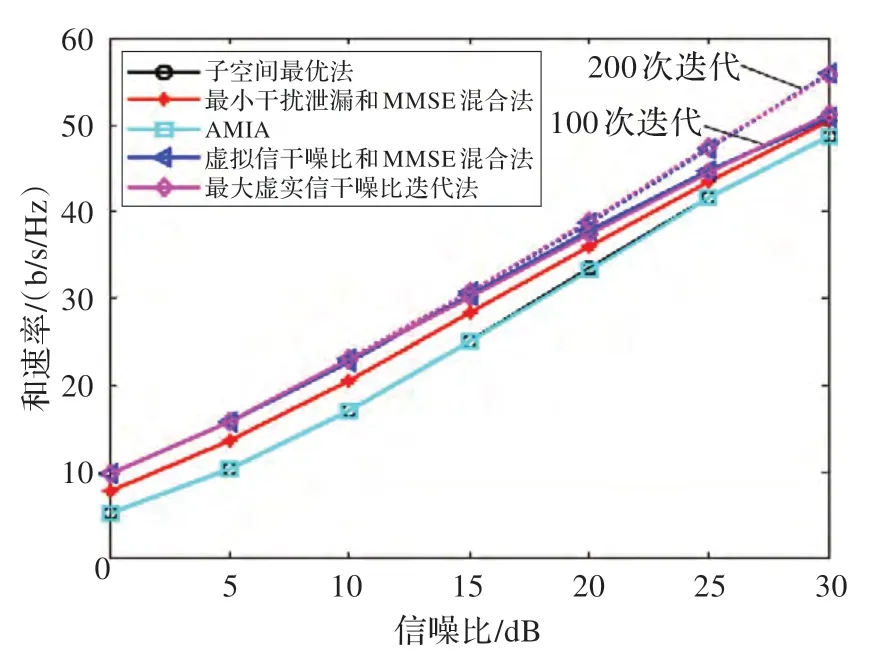
圖5 [6×6，3]3 不同迭代次數情況下和速率與信噪比的關系

圖5 和圖6 測試的是迭代次數對算法性能的影響，圖5 表示的是在[6×6，3]3條件下，增大文中算法的迭代次數時和速率性能變圖4[6×6，2/3]3時和速率與信噪比的關化曲線，虛線和實線分別表示迭代200 次和100 次情況下的曲線圖。由圖可知，文中提出的算法在迭代次數增加時，其和速率仍有提高，但幅度較小，此時以犧牲運算復雜度來提高系統容量。圖6 則更為直觀地表示在[4×4，2]3條件下，信噪比為20 dB 時，子空間最優法以及文中算法的和速率隨迭代次數 的變化趨勢，觀察圖中曲線，再次驗證了文中算法性能優于子空間最優法。在迭代次數為100 次時和速率上升趨勢不再明顯，迭代次數增加到200 次時性能僅有微小幅度的提高，之后趨于穩定，這也驗證了算法的收斂性。

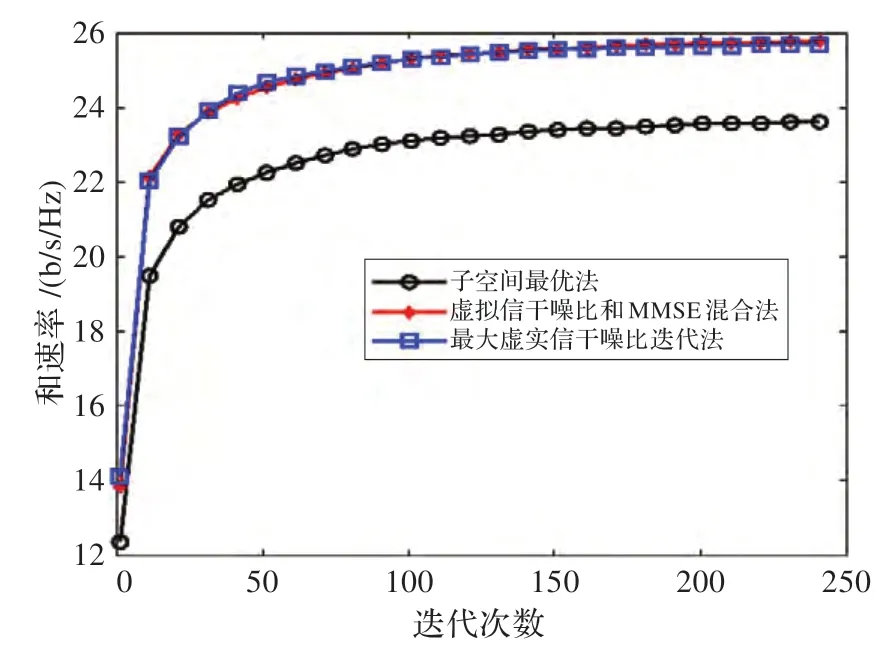
圖6 [4×4，2]3 信噪比不變時和速率與迭代次數的關系

5 結論

本文提出了基于虛擬信干噪比以及MMSE 準則的迭代算法，給出了算法推導過程，借助數值仿真評估了其性能，仿真結果表明其性能優于最優小子空間、AMIA、以及最小均方誤差迭代等算法，特別是在發送數據流小于算法自由度時性能提升更為明顯。未來的工作可以進一步考慮在信道估計有誤差時預編碼矩陣的調整策略。

[1] Goldsmith A，Jafar S A，Jindal N，et al.Capacity limits of MIMO channels[J].Selected Areas in Communications，2003，21（5）：684-702.

[2] Zakhour R，Ho Z K M，Gesbert D.Distributed beamforming coordination in multicell MIMO channels[C]//IEEE 69th Vehicular Technology Conference，Barcelona，2009：1-5.

[3] Peel C B，Hochwald B M，Swindlehurst A L.A vector-perturbation technique for near-capacity multiantenna multiuser communication-part I：channel inversion and regularization[J].IEEE Transactions on Communications，2005，53（1）：195-202.

[4] Spencer Q H，Swindlehurst A L，Haardt M.Zero-forcing methods for downlink spatial multiplexing in multiuser MIMO channels[J].IEEE Transactions on Signal Processing，2004，52（2）：461-471.

[5] Jorswieck E A，Larsson E G.The MISO interference channel from a gametheoretic perspective：A combination of selfishness and altruism achieves pareto optimality[C]//IEEE International Conference on Speech and Signal Processing，Las Vegas，2008：5364-5367.

[6] Le-Nam Tran，Juntti M，Hong Een-Kee.On the precoder design for block diagonalized MIMO broadcast channels[J].IEEE Communications Letters，2012，16（8）：1165-1168.

[7] Fang Wei，Sun Huan，Chen Jinhui.Ordered precoder designs for MIMO interference channels based on interference alignment[C]//IEEE 75th Vehicular Technology Conference，Yokohama，2012：1-4.

[8] Peters S W，Heath R W.Cooperative algorithms for MIMO interference channels[J].IEEE Transactions on Vehicular Technology，2011，60（1）：206-218.

[9] Alnajjar K，Aggarwal V，Vaishampayan V A，et al.Aligned precoder designs for interference channels based on chordal distance[C]//46th Annual Conference on Information Sciences and Systems，Princeton，2012：1-5.

[10] Raj Kumar K，Xue Feng.An iterative algorithm for joint signal and interference alignment[C]//IEEE International Symposium on Information Theory Proceedings，Austin，2010：2293-2297.

[11] Peters S W，Heath R W.Interference alignment via alternating minimization[C]//IEEE International Conference on Speech and Signal Processing，Taipei，2009：2445-2448.

[12] Zhu B，Ge J，Li J，et al.Subspace optimisation-based iterative interference alignment algorithm on the grassmann manifold[J].Communications，IET，2012，6（18）：3084-3090.

[13] Le Chung，Dimitrov E，Moghaddamnia S，et al.Performance investigation of MMSE-based interference alignment for multiuser MIMO UWB[C]//IEEE International Conference on Ultra-Wide-band，Bologna，2011：170-174.

[14] Zhou Ruixue，Lv Tiejun，Long Wei.A distributed iterative interference alignment scheme for K-User MIMO Interference Channel[C]//8th International Conference of Wireless Communications Networking and Mobile Computing，Shanghai，2012：1-4.

[15] Yu Heejung，Youngchul Sung，Haksoo Kim，et al.Beam tracking for interference alignment in slowly fading MIMO interference channels：A perturbations approach under a linear framework[J].IEEE Transactions on Signal Processing，2012，60（4）：1910-1926.

[16] Gomadam K，Cadambe V R，Jafar S A.A distributed numerical approach to interference alignment and applications to wireless interference networks[J].IEEE Transactions on Information Theory，2011，57（6）：3309-3322.

[17] Ghasemi A，Motahari A S，Khandani A K.Interference alignment for theKuser MIMO interference channel[C]//IEEE International Symposium on Information Theory Proceedings，Austin TX，2010：360-364.