電力系統低頻振蕩綜合預警方法研究

劉福潮，邢 晶，王維洲，姜希偉，但揚清，劉文穎

(1.國網甘肅省電力公司電力科學研究院，甘肅 蘭州 730050；2.國網冀北電力公司電力調度控制中心，北京 100053；3.華北電力大學電力與電子工程學院，北京 102206)

0 引言

隨著我國電網互聯程度的不斷加大，大規模區域電網的形成以及全國聯網局面的不斷深化，電力系統的穩定運行越來越受到低頻振蕩的影響，并且互聯電網的功率輸送能力也受其制約。因此，對電力系統低頻振蕩的預警技術進行研究，提前掌握可能發生的振蕩模式，及時采取手段進行預防控制，對滿足電力系統運行經濟性的要求，適應不斷擴大的電網規模，提高電力系統運行極限意義重大。

傳統的阻尼比預警方法僅能區分振蕩類型，無法反映強相關機組的參與程度和振幅等信息；而基于小干擾特征值的實用化指標則能對振蕩模式進行更加詳盡的描述。但是阻尼比的指標和小干擾特征值的實用化指標都與具體的振蕩模式對應，不能從整體上對系統發生低頻振蕩的可能性進行描述。在綜合考慮系統運行方式和運行參數對低頻振蕩影響的基礎上，本文根據阻尼比的指標和小干擾特征值的指標提出了一種低頻振蕩綜合預警方法。

1 低頻振蕩的產生機理

低頻振蕩的產生機理主要集中在負阻尼機理、強迫振蕩機理(共振機理)、非線性機理(分叉和混沌)和強共振機理等方面。其中，負阻尼機理、非線性機理和強共振機理都與電力系統的固有結構和運行參數有關；強迫振蕩機理與電力系統的擾動信號有關。

在實際應用中，基于負阻尼機理的Prony分析在工程上被廣為接受。由于各個振蕩模式之間的相互作用，因此，考慮多種機理的相互配合及各項系統運行的影響因素，建立有效評價系統低頻振蕩的綜合預警指標，對于大電網低頻振蕩預警的工程實踐相當有意義。

2 低頻振蕩的實用化模型分析

本文采用發電機3階實用模型，負荷只考慮電壓靜特性、網絡線性，且多機系統只計及轉子動態的系統，其線性化狀態方程如式(1)所示。

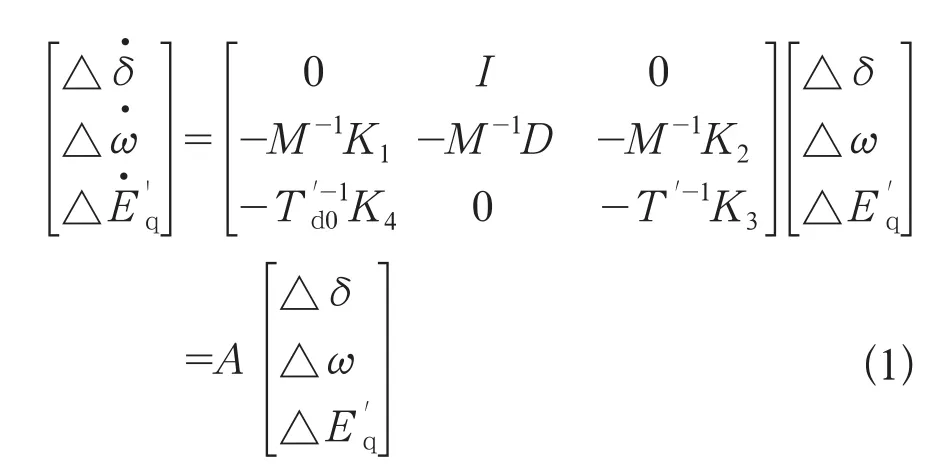
其中，A為系統狀態矩陣，M，D分別為轉子慣性時間常數及阻尼系數，I為單位矩陣。

由于風電機組定轉子之間結構的特殊性，其一般不屬于系統的某個振蕩模式，即不參與系統振蕩；但是隨著風電在電網中滲透率的增加，則必須考慮大規模風電集中接入的影響。可在電力系統綜合程序(PSASP 6.28)中的實用模型基礎上，加入大規模接入的風電參考模型，構建系統小干擾分析的實用化模型，以此作為低頻振蕩預警系統開發的理論基礎。

對于采用異步發電機的風力發電機組，可以采用式(2)所示的異步發電機實用3階模型。

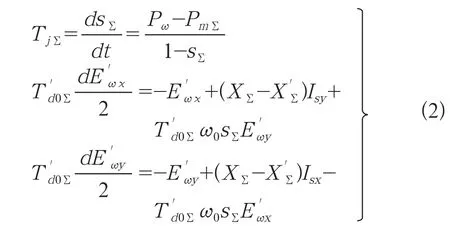
對于雙饋型風力發電機組，其建模主要包括雙饋型風力發電機組動態建模和換流器建模。在同步旋轉的dq坐標系下，根據雙饋型風力發電機的電壓方程和磁鏈方程，以及其無功控制部分和有功控制部分方程，則可以得到雙饋型風力發電機組小擾動分析的7階狀態矩陣如式(3)所示。

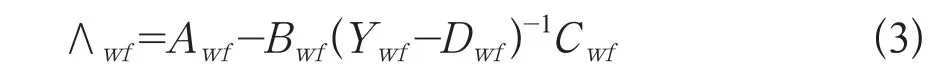
其中，∧wf為系統狀態矩陣，其特征值反映系統的小擾動穩定性及低頻振蕩模式，特征向量反映相應的系統的振蕩模式及特性，Awf，Bwf，Cwf和Dwf為包含雙饋機組模型的雅可比矩陣，Ywf為風電場對應的節點的矩陣(按實際風電場情況計算)。

其中，

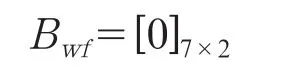
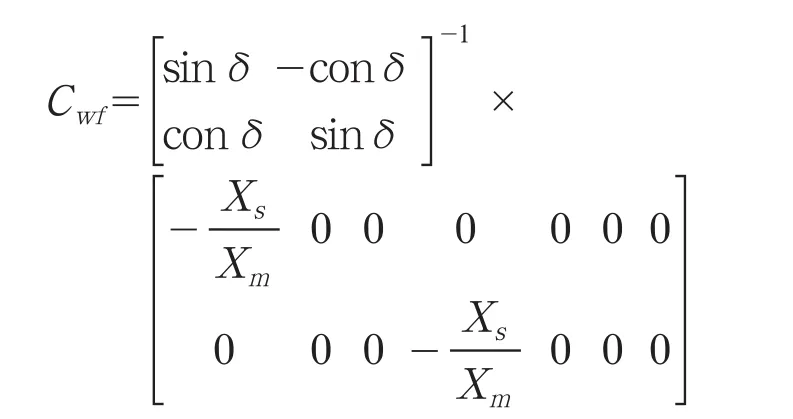
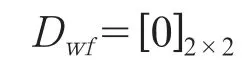
形成雙饋型風力發電機組的狀態矩陣后，對式(1)所示的全系統線性化狀態矩陣進行擴展，即可得到修正后的全系統狀態矩陣。

3 綜合預警指標的計算及修正

3.1 阻尼比的指標計算

阻尼比的指標既是綜合預警指標的組成部分，又為低頻振蕩預警提供了詳細的振蕩模式信息。

阻尼比的指標計算主要包括利用逆迭代轉Ray leigh(瑞利)商迭代法對系統的狀態矩陣進行特征分析，得到狀態矩陣的特征值和特征向量，進而計算每一個特征值所對應振蕩模式的機電回路相關比和機組相關因子等信息。通過阻尼比的指標對系統的主導振蕩模式進行篩選，并根據相關因子確定該振蕩模式的強相關機組和重點線路。

由于逆迭代轉Ray leigh商迭代法能夠求解指定頻率范圍的特征值，并且不受矩陣階數的的限制，被廣泛應用于工程實際。其流程如圖1所示。

對于計算出的全系統n個特征值λi=αi+jΩi，i=1，2,……n。每個特征值所對應自然振蕩頻率的計算如式(4)所示。

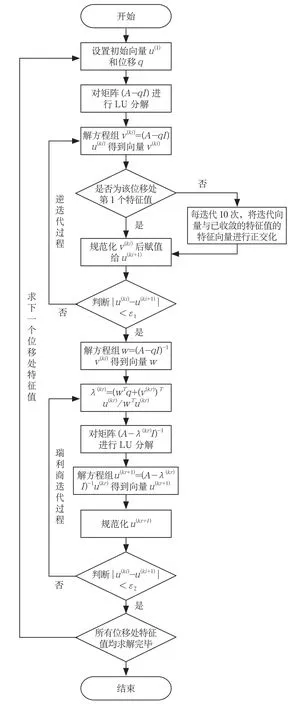
圖1 逆迭代轉Rayleigh商迭代法流程

阻尼比的計算如式(5)所示。

第k臺發電機對第i個振蕩模式的相關因子如式(6)所示。

則該振蕩模式的機電回路相關比如式(7)所示。

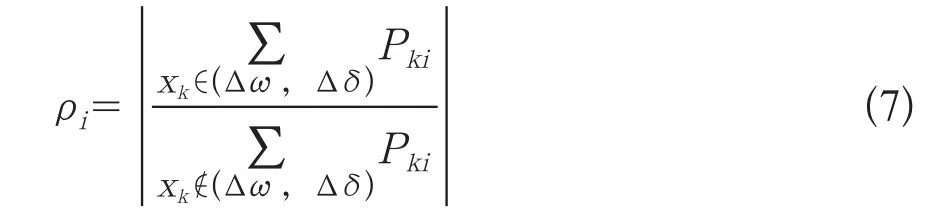
3.2 小干擾特征值的實用化指標計算

由于由振蕩模式的特征值計算出的阻尼比只能區分振蕩類型，而不能反映強相關機組的參與程度和振蕩幅值等信息；下文根據所計算出的主導振蕩模式特征值與特征向量，提出了小干擾特征值的實用化指標計算方法，以對振蕩模式進行更詳細、更具體的描述。

2種振蕩模式的模態如圖2所示。模態圖是將模態的特征向量作為離散點繪制到平面直角坐標系上，其中每一個離散點代表一個發電機組。圖2（a）中部分機組與原點附近的其他機組相距較遠，是這些機組與主網之間的振蕩模式，并且距離原點越遠的機組振蕩越劇烈。圖2(b)中幾乎所有機組都在原點附近，沒有振蕩現象發生。

因此，可以用特征向量中的散點與原點的距離對該振蕩模式進行進一步的描述。某一振蕩模式αi+jΩi小干擾特征值實用化指標的計算方法如下：

(1) 計算特征向量中每一個散點(xij，yij)與原點的距離lij；

(2) 找出lij≥0.1的點；

(3) 計算符合(2)中的條件的lij的平均值，即為小干擾特征值的指標Ri，若沒有符合條件的點，則Ri=0。

3.3 電力系統低頻振蕩綜合預警指標

對低頻振蕩產生影響的系統運行方式主要包括：電網長鏈結構和弱聯絡線，抽水蓄能電站以抽水方式運行，直流輸電控制系統、控制模式及交、直流間相互作用。

對低頻振蕩產生影響的系統運行參數主要包括：短路電流、線路輸送功率、主電站備用功率、區域功率以及負荷的波動。

考慮系統運行方式和運行參數對低頻振蕩的影響，用di，i=1，2，……8，表示電網中是否存在所述情形。若存在所述的某一種情況，則相應的di=-1；否則di=0。例如：若系統中包含長鏈結構或弱聯絡線，則d1=-1；否則d1=0。

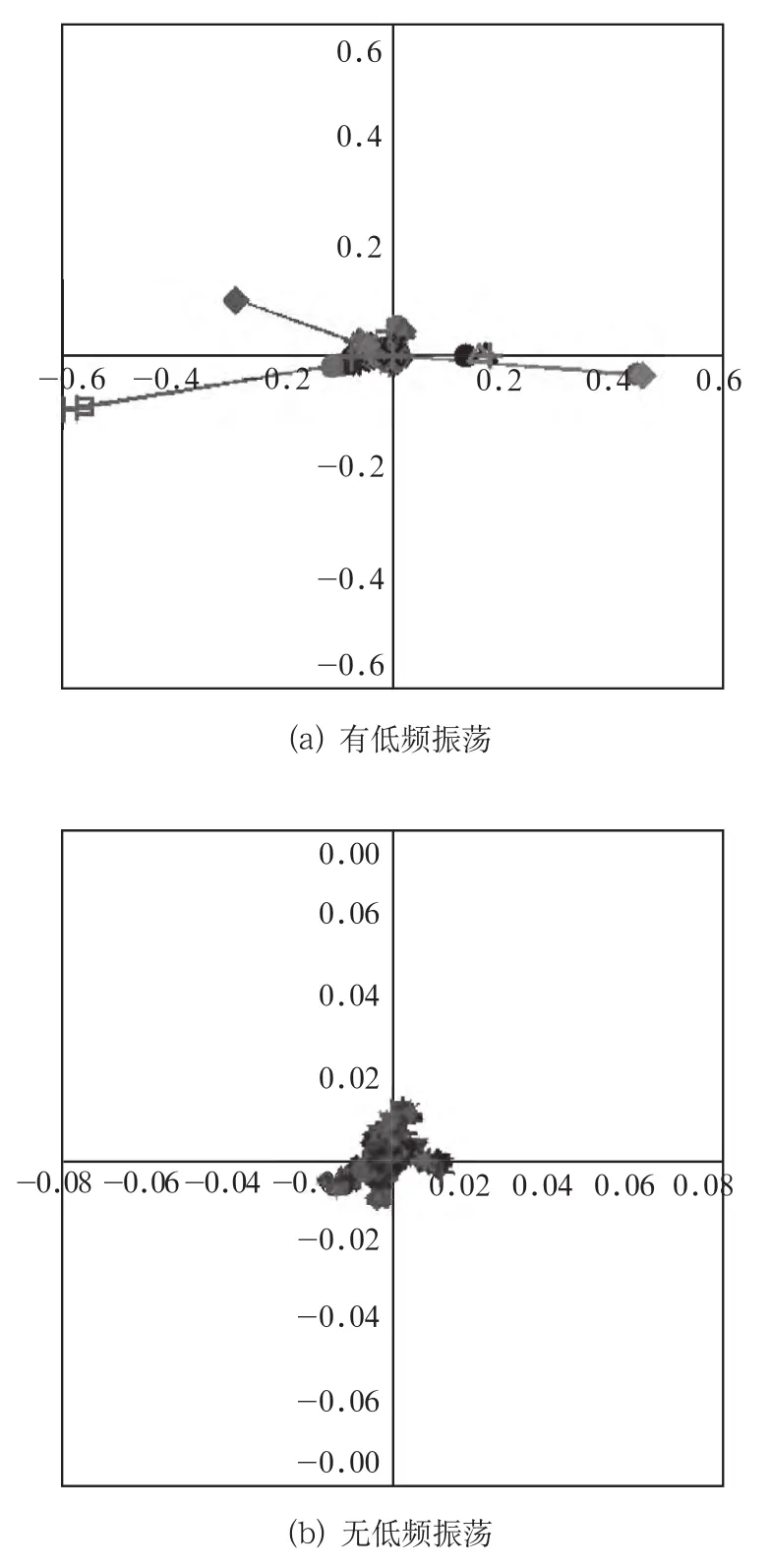
圖2 2種振蕩模式的模態圖

設綜合預警指標為D，則：

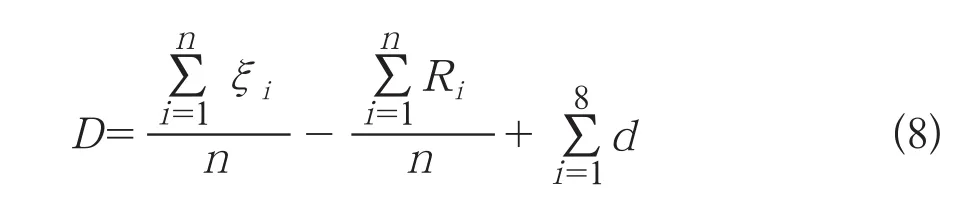
從上述指標可以看出，D越小，系統的網架結構越薄弱，主導振蕩模式的阻尼越弱，振蕩模式中機組偏離原點的距離越遠，發生低頻振蕩的可能性也越高；D越大，系統的網架結構越堅強，主導振蕩模式的阻尼也越大，機組離原點的距離也越近，發生低頻振蕩的可能性也越低。

3.4 仿真驗證

以甘肅電網為研究背景，選取甘肅電網冬天負荷某一運行斷面進行小干擾穩定分析計算，所求解的全部特征值對應的特征根分布如圖3所示。圖中所有特征根均位于虛軸左側，系統是穩定的。

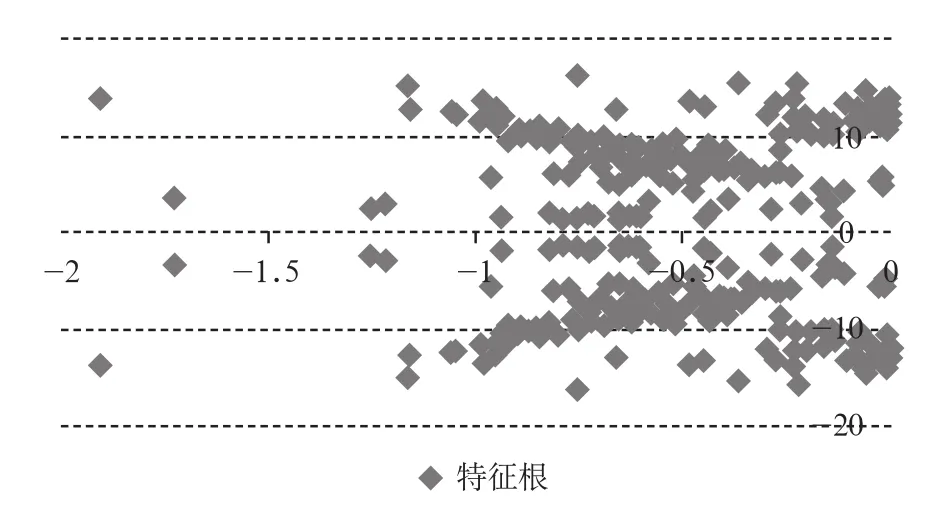
圖3 全部特征根分布

經過篩選和比較，得到該運行方式下的12個主導振蕩模式及其強相關機組，如表1所示。

對每個振蕩模式的小干擾特征值指標進行計算，其結果如表2所示。

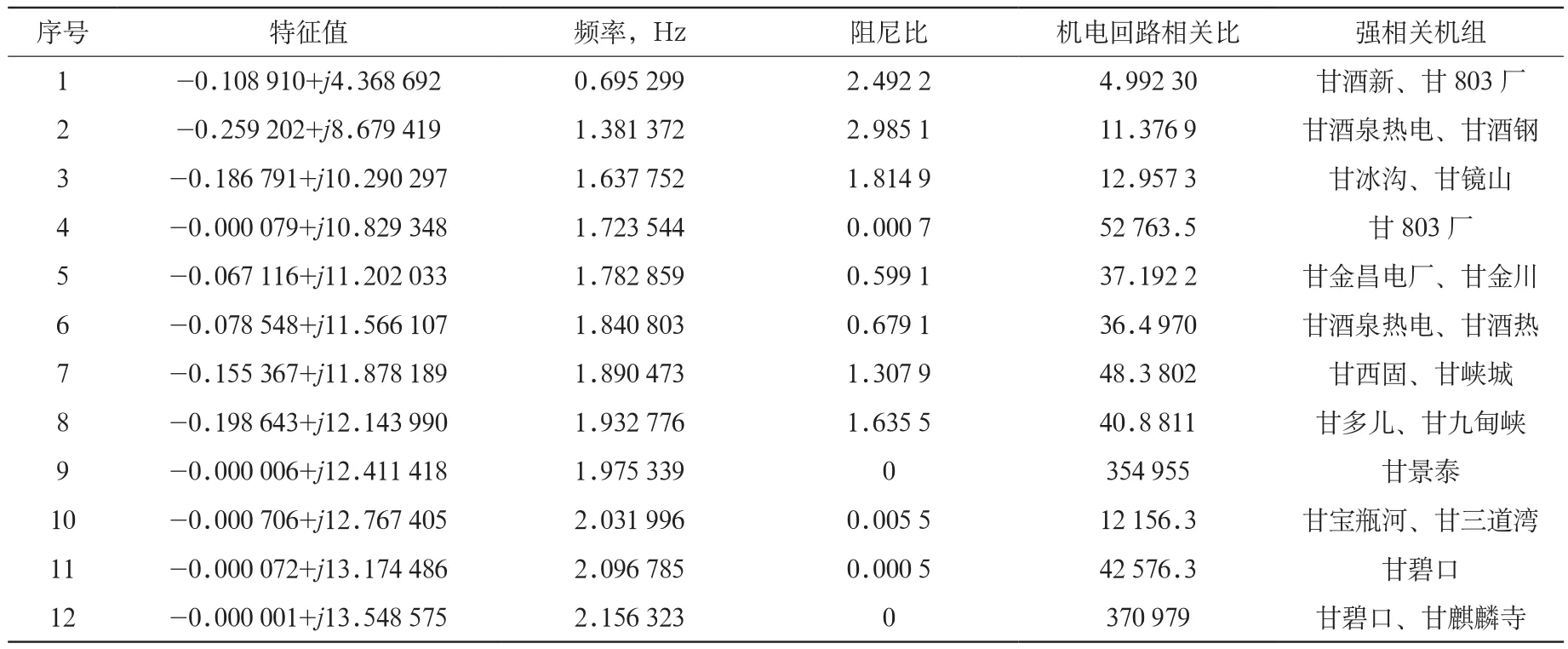
表1 主導振蕩模式及其強相關機組

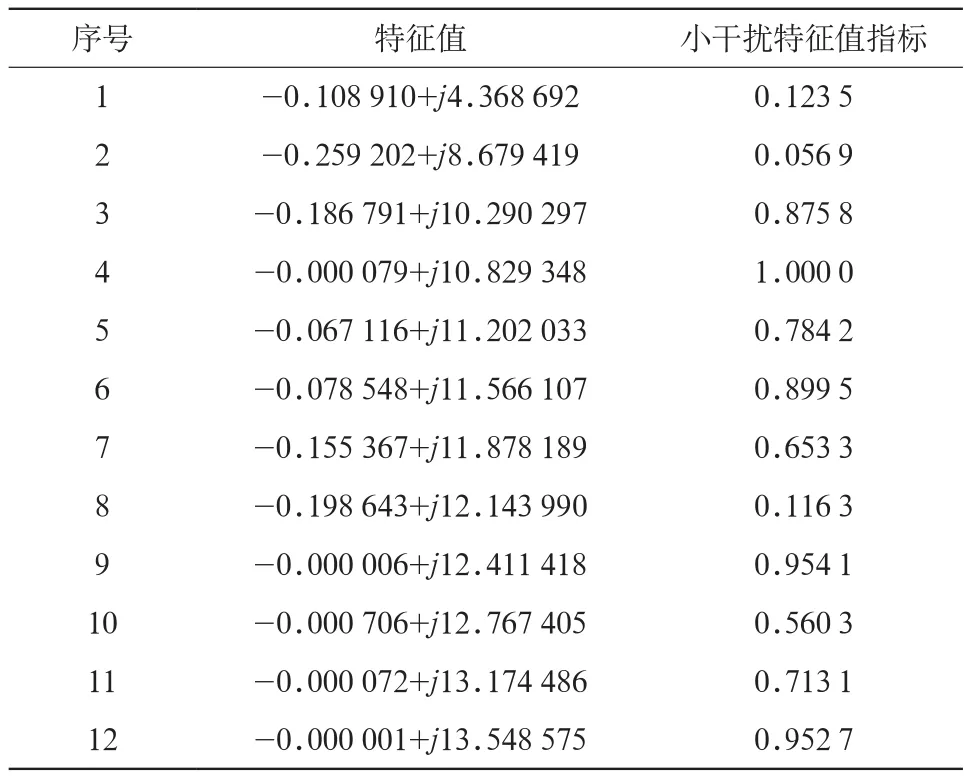
表2 小干擾特征值的指標計算結果

完成阻尼比指標和小干擾特征值指標的計算后，考慮系統的運行狀態A：

(1) 山丹-張掖330 kV線路輸送功率達到穩定極限；

(2) 主網負荷出現500 MW功率波動。

再對系統運行方式和系統運行參數對低頻振蕩的影響進行判斷，如表3所示。

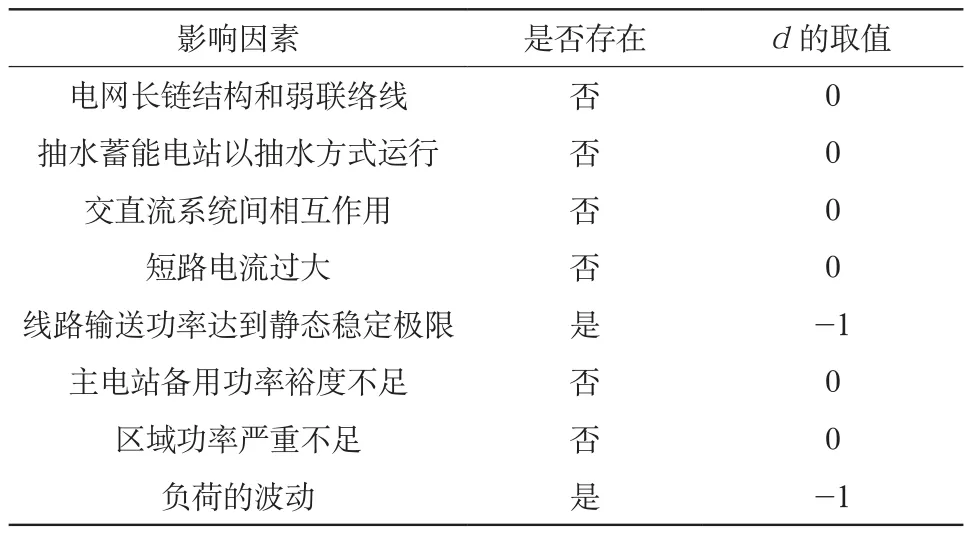
表3 系統運行方式和參數對低頻振蕩影響參數的確定

最后根據式(8)計算得到電力系統低頻振蕩綜合預警指標為D=-1.68。利用PSASP暫態計算模塊對A運行狀態進行仿真計算，山丹-張掖一回330 kV線路1 s三相短路、1.1 s故障切除并且重合不成功時，得到功率振蕩曲線。曲線表明A運行狀態下，系統失穩，存在低頻振蕩問題。

適當改變某些發電機組的出力，降低山丹-張掖輸送功率至靜態穩定極限以下后，按照上述過程重新計算，綜合預警指標D=0.07。此時再次應用PSASP軟件仿真計算，結果表明山丹-張掖一回330 kV線路1 s三相短路、1.1 s故障切除并且重合不成功時，沒有發生振蕩現象。

綜上所述，在A運行狀態下，系統失穩，存在低頻振蕩問題，其D值為-1.68；在調整后的運行狀態下，系統穩定，沒有發生振蕩現象，其D值為0.07。因此，可以看出綜合預警指標D能夠反映系統發生低頻振蕩可能性的大小，具有一定的參考價值。

4 結束語

本文在考慮大規模風電集中接入的基礎上建立了電力系統低頻振蕩分析的全系統實用數學模型，利用逆迭代轉Ray leigh商迭代法對系統狀態方程進行特征分析，求解特征值和特征向量，并根據計算結果篩選主導振蕩模式，進一步查找每個振蕩模式的強相關機組和重點線路，并對低頻振蕩預警的阻尼比指標和特征值指標進行實用化計算，在考慮低頻振蕩多種影響因素的基礎上提出了低頻振蕩綜合預警指標。算例仿真結果表明，綜合預警指標能夠反映系統發生低頻振蕩可能性的大小，該綜合預警方法可行且有效。

1 倪以信，陳壽孫，張寶霖．動態電力系統的理論和分析[M]. 北京：清華大學出版社，2002．

2 王彥敏．基于WAMS的電力系統低頻振蕩監測與控制方法研究[D]．北京：華北電力大學，2008．

3 郝思鵬．電力系統低頻振蕩綜述[J]．南京工程學院學報，2003，13(1)：1-8．

4 崔小磊．電力系統低頻振蕩在線預警系統研究[D]．北京：華北電力大學，2005．

5 吳復霞．電力系統低頻振蕩的分析和控制[D]．杭州：浙江大學，2007．

6 王鐵強，賀仁睦，王衛國，等．電力系統低頻振蕩機理的研究[J]．中國電機工程學報，2002，12(2)：21-25．

7 王鐵強．電力系統低頻振蕩共振機理的研究[D]．北京：華北電力大學，2001．

8 王 青，閔 勇，張毅威．電力系統低頻振蕩的機理研究和主要分析方法[J]．電氣應用，2006，7(25)：1-4．

9 Cansin Y．Evrenosoglu，A li Abur，Ergun Ak leman.Th ree dim ensional visualization and animation of travelling w aves in pow er sy stem s[J]．Electric Pow er System s Research，2007，5(7)：876-883．

10 李 晶．變速恒頻雙饋風電機組動態模型及并網控制策略的研究[D]．保定：華北電力大學，2004．

11 周志強．雙饋感應風電機組電磁暫態建模、控制及實證研究[D]．吉林：東北電力大學，2008．

12 蔣爾雄．關于Ray leigh商迭代法的理論基礎[J]．高等學校計算數學學報，1990，13(1)：78-96．

14 李 芳，郭 劍，吳中習，等．基于PC機群的電力系統小干擾穩定分布式并行算法[J]．中國電機工程學報，2007，11(31)：7-13．

15 X ing Jing，Liu W eny ing，Liu Qian，et al．GDI and openGL-based imp lementation of visualization fo r th e g rid m ain tenan ce p lann ing sup por t system[C]．Shanghai：APPEEC，2012．