SRSARV模型與GARCH及SV模型的關系研究
張 超,孟昭為
(山東理工大學 理學院,山東 淄博 255049)
SRSARV模型與GARCH及SV模型的關系研究
張 超,孟昭為
(山東理工大學 理學院,山東 淄博 255049)
平方根隨機自回歸波動模型(SRSARV)是一個具有較強包容性的模型.針對此特點討論了該模型與GARCH類模型及SV類模型的具體包含關系,并對給出的相關定理予以證明,為在實際問題中根據具體情況選擇模型提供參考.
GARCH模型;隨機波動;狀態空間;SRSARV模型
SRSARV模型是一個具有較強包容性的模型,它連接了GARCH類模型及SV類模型.下面總結一下它們之間的關系.
1 GARCH類模型簡介

(1)
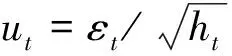
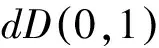
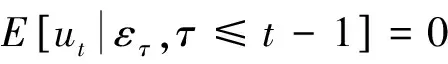
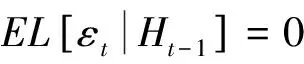
2 SRSARV模型與ARCH模型的關系
許啟發等[3]給出了介紹SRSARV模型與ARCH模型的關系的定理,如下.
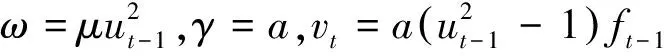
但是定理提出者沒有給出具體的定理推導過程,下面本文作者在參考借鑒基礎上給出自己的理解和證明.
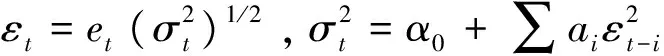
3 SRSARV1模型與半強GARCH(1,1)模型的關系
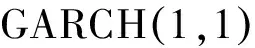
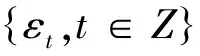

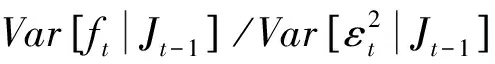
ht+1=ft,Jt=It,β=γ-α
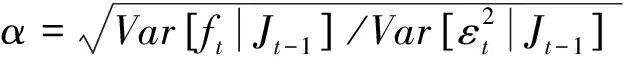
但是定理提出者沒有給出具體的定理推導過程,下面本文作者在參考借鑒基礎上給出自己的理解和證明.
證明 (必要性)

(充分性)

4 SRSARV模型與弱GARCH模型的關系
MeddahiN等[5]給出了介紹SRSARV模型與弱GARCH模型的關系的定理,如下.

但是定理提出者沒有給出具體的定理推導過程,下面本文作者在參考借鑒基礎上給出自己的理解和證明.
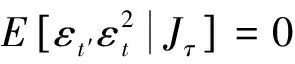
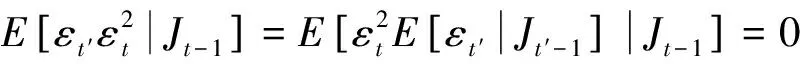
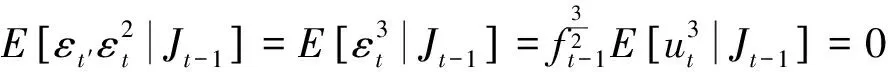
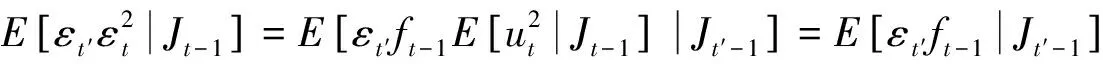
但是
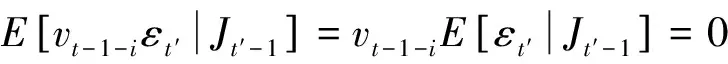
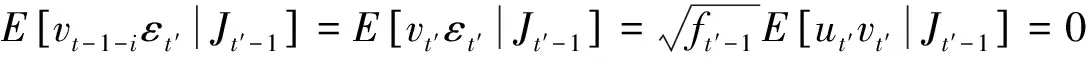
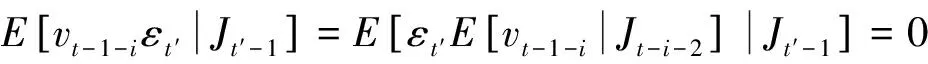
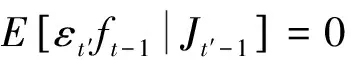
5 SRSARV模型與非對稱GARCH模型的關系
隨著金融理論不斷發展和實證研究的進一步深入,越來越多的證據表明,在股票市場和匯率市場,金融資產收益率的波動率不僅具有時變性、集群性還具有非對稱性.很多國家和地區的金融市場,特別是股票市場,存在顯著的非對稱性.國內外學者對此做了很多研究.
其中主要的非對稱GARCH模型有以下幾類[6].
模型1 GJR-GARCH
(1)
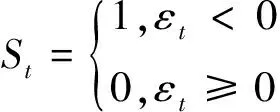
模型2 A-GARCH
(2)
模型3 NA-GARCH
(3)
模型4 VGARCH
(4)
那么,非對稱GARCH(1,1),如GJR-GARCH(1,1)、A-GARCH(1,1)、NA-GARCH(1,1)、VGARCH(1,1),都是SRSARV(1)類模型.
許啟發等[3]給出了介紹SRSARV模型與非對稱GARCH模型的關系的定理,如下.

但是定理提出者沒有給出具體的定理推導過程,下面本文作者在參考借鑒基礎上給出自己的理解和證明.

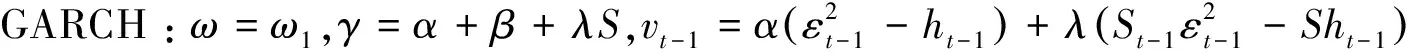
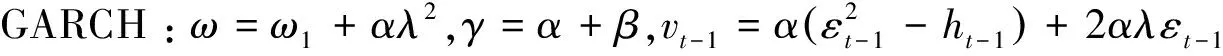
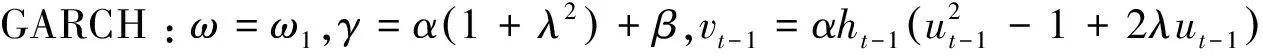
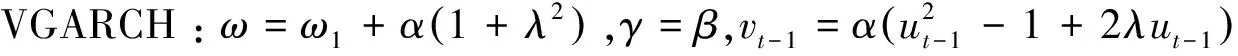
定理1-定理4表明,SRSARV模型包含半強GARCH模型(更包含強GARCH模型);包含弱GARCH模型中的絕大部分;同時也包含各種非對稱、非線性GARCH模型.盡管弱GARCH模型具有良好的聚合性質,但它不能捕獲杠桿效應和偏度,然而 SRSARV模型卻能做到這一點.
6 SRSARV模型與SV模型的關系
MeddahiN,RenaultE(2004)在參考文獻[6]中給出了介紹SRSARV模型與SV模型的關系的定理,如下.
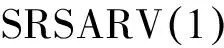
(5)
ht-1=ω+γht-1+vt
(6)
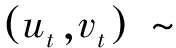
但是定理提出者沒有給出具體的定理推導過程,下面本文作者在參考借鑒基礎上給出自己的理解和證明.
[1]MeddahiN,RenaultE.AggregationandmarginalizationofGARCHandstochasticvolatilitymodels[J].EconomicsLetters,1999,64:31-36.
[2]DuanJC.AugmentedGARCH(p,q)processanditsdiffusionlimit[J].JournalofEconometric,1997,79:97-127.
[3] 許啟發,張世英.金融波動的平方根隨機波動模型[J]. 系統工程理論方法應用,2004,13(6):561-568.
[4]AndersenTG.Stochasticautoregressivevolatility:aframeworkforvolatilitymodeling[J].MathematicalFinance,1994,4(2):75-102.
[5]MeddahiN,RenaultE.Temporalaggregationofvolatilitymodels[J].JournalofEconomics,2004,119:355-379.
[6] 詹姆斯·D·漢密爾頓.時間序列分析[M].北京:中國社會科學出版社,1999:446-489.
[7] 杜子平,張世英.SV模型的聚合及邊際化研究[J].系統工程理論方法應用,2002,11(2):173-176.
(編輯:姚佳良)
Relations between SRSARV model and GARCH or SV models
ZHANG Chao, MENG Zhao-wei
(School of Science, Shangdong University of Technology, Zibo 255049, China)
The square-root stochastic autoregressive volatility model (SRSARV) is a strong inclusive model, and for this specific feature of the model, we discussed the include class relations between SRSARV type and GARCH type models or SV models , and proved relevant theorems. The results would provide references for selecting models in practice.
GARCH; stochastic volatility; state-space; SRSARV
2015-01-09
張超, 男,zhangchaolg@163.com; 通信作者: 孟昭為,男,sdlgmzw@126.com
1672-6197(2015)06-0046-04
O213
A

