透鏡列陣光學系統的小尺度不均勻性

鄭建洲，曹曉君，關壽華，穆婷婷

(大連民族學院物理與材料工程學院，遼寧大連116605)

采用列陣空間束勻滑技術［1-2］，可有效地消除入射激光束近場分布不均勻對靶面輻照的影響，能夠控制靶面輻照光強的包絡分布，得到接近平頂分布的焦斑，并能有效地抑制旁瓣產生，使靶面的相對光強包絡分布對入射激光場的近場分布不敏感。但是，由于列陣均勻輻照光學系統的各個子束間的干涉，必然在焦斑光強包絡上產生空間高頻成分的多光束干涉效應的微米量級的小尺度強度調制［3-4］。即使使用最佳的包絡分布輻照靶面，由于空間高頻成分的存在，整體的不均勻性仍難以控制在1%的范圍內。雖然這種小尺度的不均勻性可以被等離子體內的橫向熱傳導效應平滑掉，但是，在直接驅動中，輻照加熱初期的小尺度不均勻性會直接烙印在靶面，引起流體力學不穩定性，在內爆過程中被進一步放大后，將影響靶丸的對稱壓縮，使靶丸變形甚至破裂，而靶丸變形會使實現點火所需的激光能量增大［5］;在間接驅動中，小尺度不均勻性在等離子體中會引起光學成絲，進而會引起SRS、SBS等非線性效應，這不但會降低X射線的轉換效率，而且非線性效應會產生超熱電子，使靶芯預熱，從而影響靶丸壓縮［6］。因此，無論是直接驅動還是間接驅動，都必須消除小尺度的干涉斑紋引起的不均勻性。

為了能夠更有效地發揮列陣光學系統在實現靶面均勻輻照的作用，有必要對透鏡列正光學系統的小尺度不均勻性的變化規律和減小的方法進行研究。本文應用波動光學推導出了LA系統靶面光強分布公式和表征小尺度不均勻性的多光束干涉條紋間距公式，并通過衍射積分理論數值計算證明了該公式。有研究表明，用離焦打靶的方法可以有效地改善LA的大尺度幅照均勻性［3］，而我們通過理論和數值計算研究發現，對LA系統適當離焦時還可以有效地改善小尺度不均勻性。

1 透鏡列陣光學系統的理論分析

透鏡列陣系統的原理結構如圖1，(其中L為主聚焦透鏡，LA為透鏡列陣，l為綜合焦斑寬度)。透鏡元的個數為N×N個(取N為奇數)，透鏡元口徑為d，并且D=Nd，焦距為fe，其中透鏡列陣由N×N相同的、正方形透鏡元組合而成，置于靶鏡之前。入射到透鏡列陣上的激光束被分成多個子束，在系統的組合焦面聚焦后對準近場(聚焦透鏡后焦面)的靶面實現均勻輻照。

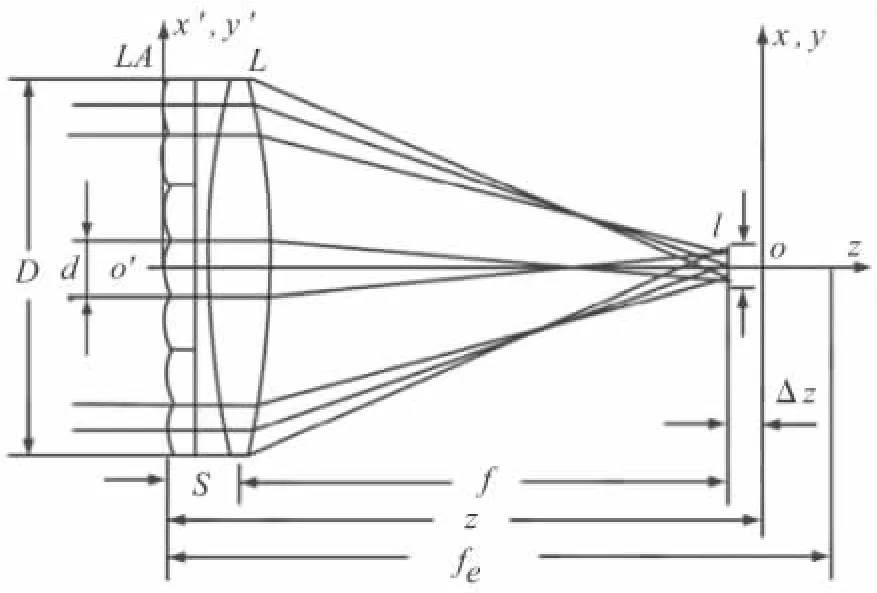
圖1 透鏡列陣均勻輻照原理圖

由幾何光學可得焦斑寬度為

對于圖1所示的透鏡列陣，從透鏡列陣輸出面至靶面的傳輸矩陣為

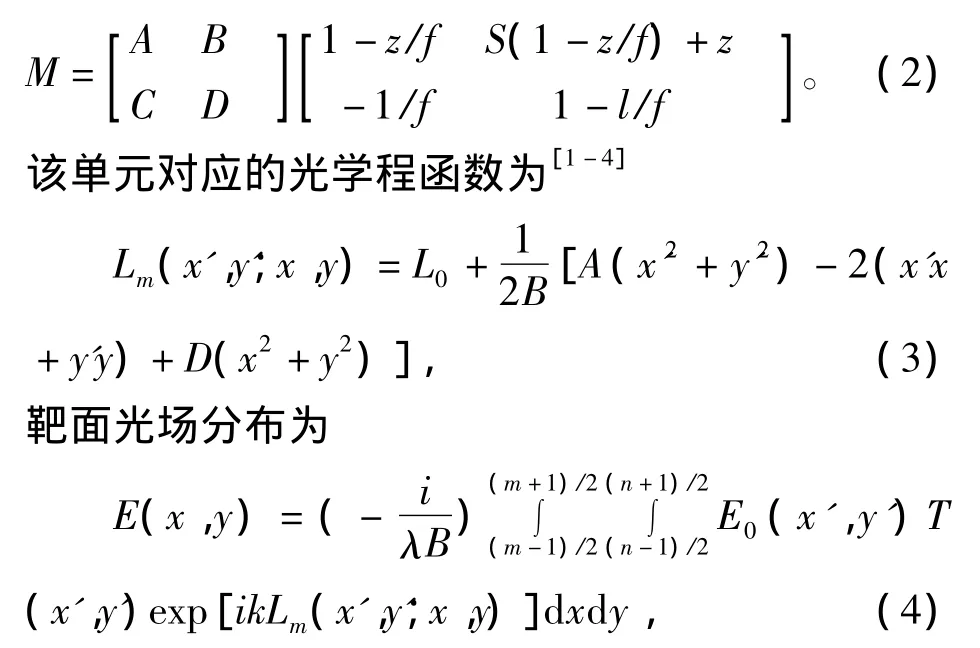
式中，x'，y'和x，y分別為輸入面和輸出面的坐標，E0(x'，y')為經LA后的光場分布(包括入射光束的振幅和位相起伏及可變焦LA引入的隨機相移)。式(4)中已假設入射光場為完全相干且偏振方向完全一致，主聚焦透鏡為一理想透鏡，LA靠近主聚焦透鏡，且主聚焦透鏡孔徑很大，不會引起附加的衍射。

(*表示復數共軛)。

根據物理光學得出透鏡列陣x方向的多光束干涉主極大的距離為

2 斑紋的統計分析

激光通過透鏡列陣后在遠場或準遠場的斑紋是子束隨機相干的結果，斑紋的光強分布顯得有些混亂無序。對這種不規則的圖樣，考慮其強度分布時只能用概率論與統計學的方法來分析計算。采用光強幾率密度分布和平均光強對比度作為表示干涉斑紋統計性質的量。

2.1 單一斑紋

當透鏡列陣元數目非常大時，對于透鏡列陣元產生的干涉斑紋，光強分布的幾率密度函數為負指數分布函數［7］，

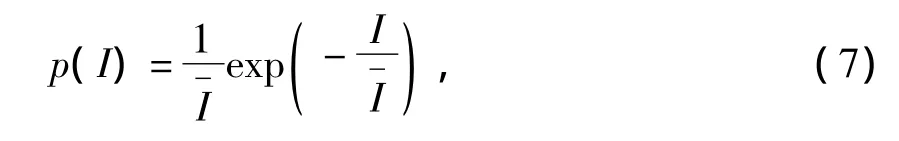
斑紋的不均勻度由強度分布的標準偏差除以平均值來定義:

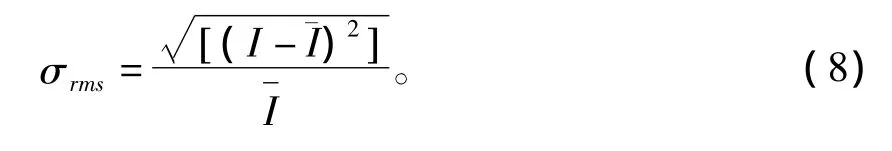
對于相干激光經過透鏡列陣后產生的斑紋，由式(7)可得，因而，代入式(8)可得此斑紋的不均勻度為1，達到最大值。

2.2 多斑紋疊加

強度分布不相關的多個斑紋獨立疊加(按光強疊加)時，光強幾率密度分布不同于單個斑紋的幾率密度分布。若各斑紋具有相同的統計性質并且平均強度相等，則N個斑紋非相干疊加后的光強幾率密度分布為［7］

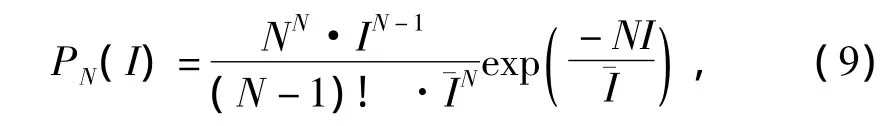
在這種情況下，零強度的幾率密度大為降低，實際上幾乎沒有零強度。

獨立疊加斑紋數N增大時，按式(9)計算光強幾率密度(ˉI～PN(I))分布變化的情況如圖2。可見，隨著斑紋數N的增加，暗的和亮的幾率密度都減小了，幾率密度的峰值移向平均強度，最后強度分布集中在平均強度附近非常窄的范圍內。由此表明，斑紋的不均勻度降低，使斑紋得到勻滑。

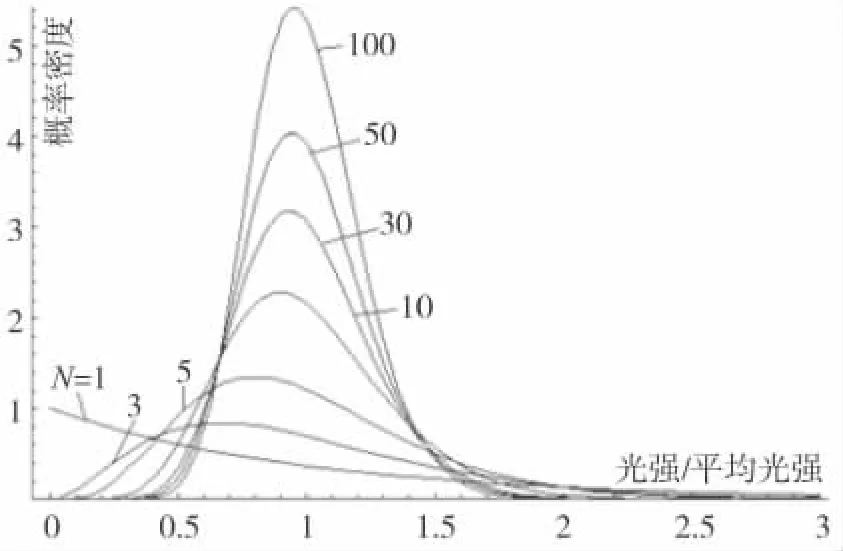
圖2 干涉斑紋按光強疊加后的光強幾率密度分布

將式(9)代入式(8)，可得N個斑紋疊加時斑紋的平均光強不均勻度為

即不均勻度反比于疊加斑紋數N的平方根。

增大獨立疊加斑紋數可降低斑紋的不均勻度，使斑紋得到勻滑，這就是消除小尺度不均勻性、實現光斑勻滑的機理。增加靶面疊加的光斑數有兩種方法。一種方法是讓多個獨立且不相關(相互交錯)的光斑同時疊加在靶面上，使光斑即時得到勻滑;另一種方法是在內爆流體動力學響應時間內讓斑紋快速變化，從時間累計的效果上得到多個獨立斑紋的疊加，從而使光斑得到勻滑。這兩種方法同時采用更可加快光斑的勻滑。

2.3 適當離焦

將靶面放置適當的離焦位置上，使各單元衍射分布不完全重疊，彼此稍微錯開［7］，在有效的抑制單元衍射效應引起的大尺度不均勻性的同時，也可使條紋各主極大之間的次極大增長到與主極大相當的強度，減小干涉條紋間隔不均勻性，從而改善系統的小尺度不均勻性。計算離焦時，在系統焦斑的位置要加上一小的改變量Δz，這里Δz是離焦量，即靶面離開最佳重疊位置的距離。

3 數值模擬

用GLAD光學軟件，建模計算了靶面上正方形透鏡列陣的三維、二維和一維光強分布、光斑尺寸以及干涉斑紋的小尺度間隔。計算參數:光波波長 λ =0.632 8 μm ，D=133 mm，LA系統單元為7×7，聚焦透鏡焦距為f=500 mm，透鏡列陣焦距為fe=11 875 mm。正方形透鏡列陣元的邊長為d=19 mm。離焦量分別為Δz=0 mm和Δz=2 mm時，三維光強分布計算結果如圖3。計算得出遠場光斑尺度為800 μm。

圖3 不同離焦量時單色激光通過硬邊透鏡列陣系統后的焦斑三維光強分布

靶面上的光強分布邊緣的強度起伏是由于單個列陣元邊緣的衍射效應產生的，而光強的中間許多高頻調制的條紋實際是各個列陣單元的子束產生的多光束干涉的結果，x，y方向的不均勻度分別為σx=8.1%，σy=9.3%。這里焦斑強度分布的不均勻性主要來自衍射引起的包絡起伏(導致大尺度不均勻性)。

當離焦量Δz=0 mm時單色激光只通過硬邊透鏡列陣系統后的焦斑二維和一維光強分布如圖4。

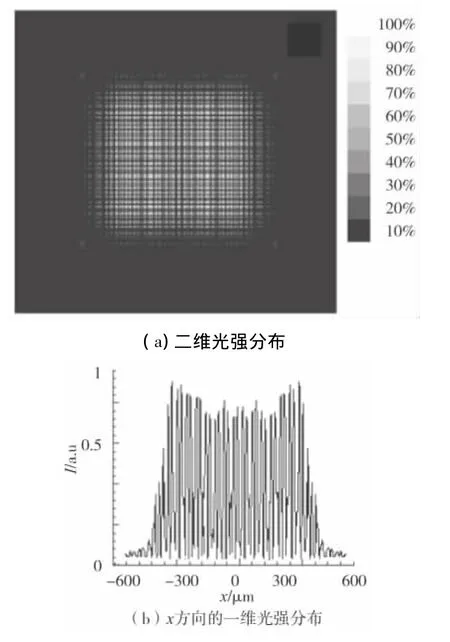
圖4 離焦量Δz=0 mm時，單色激光只通過硬邊透鏡列陣系統后的焦斑二維、一維光強分布

沿x方向焦斑中心處放大后計算LA系統焦斑上干涉條紋的結果如圖5。

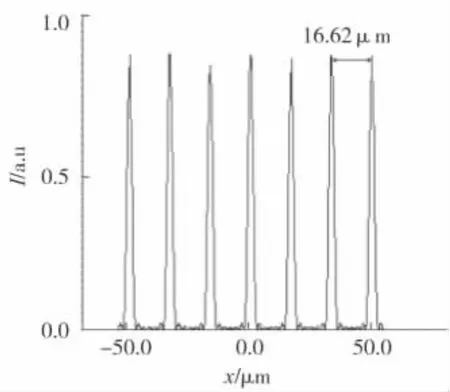
圖5 LA系統焦斑上沿x方向焦斑中心處干涉條紋放大后的結果

這一結果與根據物理光學的公式得出透鏡列陣x方向的多光束干涉主極大的距離符合得非常好。

當離焦量Δz=2 mm時單色激光通過硬邊透鏡列陣系統后的二維和一維光強分布如圖6。

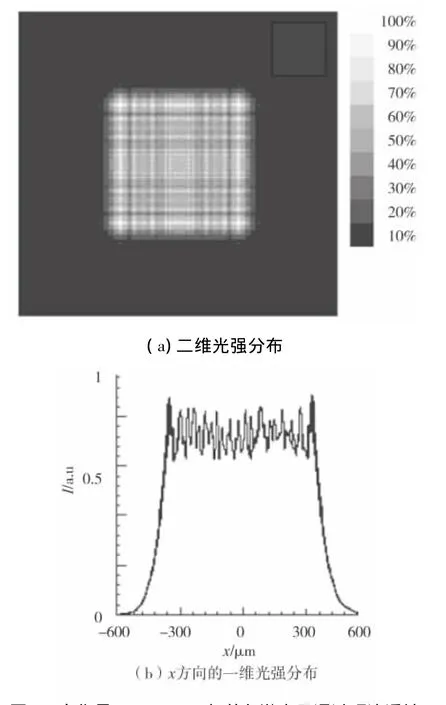
圖6 離焦量Δz=2 mm時，單色激光只通過硬邊透鏡列陣后的焦斑二維、一維光強分布

通過適當離焦，使各單元衍射分布不完全重疊，彼此稍微錯開，可降低焦斑邊緣的衍射起伏，使光強邊緣的大尺度衍射起伏在一定程度上得到抑制，同時多光束干涉產生的高頻調制的條紋變得更加密集，小尺度不均勻性還可以通過靶面材料的橫向熱傳導效應消除。當Δz=2 mm時，均勻性最好，不均勻性為σx=5.73%，能量利用率達到95.1%，大大減少了條紋小尺度的不均勻性。

考慮靶面材料的橫向熱傳導效應時，數值計算時可等效為再通過20 μm勻滑后的效果，如圖7。不均勻性為σx=4.8%，能量利用率達到η=88.4%。

4 結語

通過理論分析和數值計算研究了透鏡列陣光學系統焦斑的輻照均勻性以及小尺度不均勻性的規律。推導出LA系統靶面遠場光強分布的解析式和小尺度不均勻性的間隔公式。透鏡列陣將入射激光分割成很多子光束，它們的準近場衍射光斑在靶面疊加起來，焦斑具有比較陡峭的包絡，而且沒有一般遠場焦斑的旁瓣。由于各個子束存在多光束干涉，在焦斑內存在細密的干涉條紋，在焦斑的邊緣處還有衍射調制的較大起伏。通過適當離焦時，使各單元衍射分布不完全重疊，彼此稍微錯開，可降低焦斑邊緣的衍射起伏，使光強邊緣的大尺度衍射起伏在一定程度上得到抑制，同時多光束干涉產生的高頻調制的條紋變得更加密集，小尺度不均勻性也得到很大改善。若將橫向熱傳導平滑效應也考慮在內，多光束干涉所引起的細密條紋可進一步消除。在激光聚變中，這種適當離焦的方法用于靶面輻照初期的光斑勻滑更有意義。

［1］DENG X，LIANG X，CHENG Z，et al.Uniform illumination of large targets using a lens array ［J］.Appl.Opt.，1986，25(2):377-381.

［2］鄭建洲，于清旭，盧永軍.焦斑可調的透鏡陣列均勻輻照光學系統［J］.中國激光，2007，34(3):331-336.

［3］鄭建洲，于清旭，關壽華.正交光楔列陣光學系統小尺度不均勻性的研究［J］.光學精密工程，2009，17(1):1195-1201.

［4］ZHENG Jianzhou，ZHENG Wenyang，QINGXU Y U，et al.Improved uniformity of target irradiation by combining an Orthogonal Cylindrical Lens Array and the polarization control［J］.Proc.of SPIE，2012，7654:76540O-1-76540O8.

［5］ROTHENBERG J E，WEBER S V.The impact of beam smoothing method on direct drive target performance for the NIF［J］.Proc.of SPIE，1997，3047:736-745.

［6］PENNINGTON D M，DIXIT S N，WEILAND T L，et al.Implementaltion and performance of beam smoothing on 10 beams of the Nova laser［J］.SPIE，1997，3047:725-730.

［7］丹尼蒂J C.激光斑紋及有關現象［M］.黃樂天，王天及，譯.北京:科學出版社，1981.