基于不確定偏好信息的多屬性群決策研究

溫 馨 曾培勇 張 全 滿飛宇 陳云鶴

（1.沈陽工業(yè)大學信息學院，遼寧 沈陽110870；2.中國石油集團東北煉化工程有限公司，遼寧 沈陽110000）

0 引言

多屬性群決策問題是將各決策者給出的不同意見進行集結，從而得到群意見的問題[1]。然而在實際的群決策過程中，由于決策者自身的知識結構、判斷水平以及個人偏好等主觀因素的影響，可能會針對同一個方案（或同一屬性）給出不同形式的偏好信息。到目前為止，有關多種形式偏好信息并存的群決策問題已經(jīng)有了不少相應的解法：如文獻[2]在國際上首次提出具有不同形式偏好信息的群決策問題的研究，并給出了三種不同形式偏好信息的集結方法；文獻[3]給出了群決策中具有兩種判斷矩陣形式偏好信息的集結方法；文獻[4]分析了決策者可能給出的六種不同形式偏好信息的轉(zhuǎn)換，并運用OWA算子集結各決策者偏好信息和方案優(yōu)選的方法。

本文在研究多屬性群決策的過程中，首先將決策者給出不同形式的偏好信息進行規(guī)范化，將其轉(zhuǎn)換成一致的模糊互補偏好關系，其次，根據(jù)各決策者的偏好關系，建立優(yōu)化模型來求解各方案的排序值，即排序值越大，方案越優(yōu)。

1 問題描述

本文考慮決策者給出決策方案的偏好信息的多屬性群決策問題。為了方便敘述，采用下面的術語來描述多屬性群決策問題：

i表示決策者ek給出的語言評價值;

4）方案集合上的嚴格偏好關系：決策者認為方案Si嚴格優(yōu)越于Sj，只是在部分方案上表現(xiàn)出嚴格的偏好關系。

本文的研究在于根據(jù)決策者給出的偏好信息，求出各方案的排序值與排序。

2 提出的方法

2.1 偏好信息的規(guī)范化與集結

由于決策者給出評價偏好信息具有不同的表達形式，因此將其規(guī)范化為一致的模糊互補偏好關系[6-7]，方法如下：

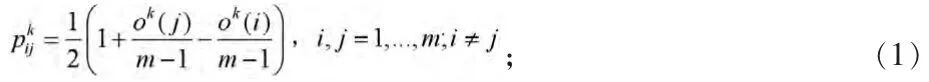
2）方案集合上的嚴格偏好關系，他們之間的模糊互補偏好關系可以被看成是絕對的，即1與0的偏好關系。

3）基于決策者給出的方案集合上的選擇子集，他們之間的模糊互補偏好關系如下：

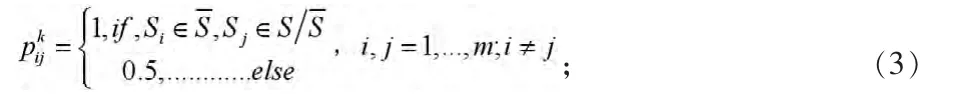
采用OWA算子對規(guī)范化的模糊互補偏好關系進行集結，記得到的結果為P=（Pij）m×m。

2.2 優(yōu)化模型建立與求解

假設方案Si的排序值為di，其中，。建立如下矩陣F：

模型（5-6）可以轉(zhuǎn)換為如下形式：

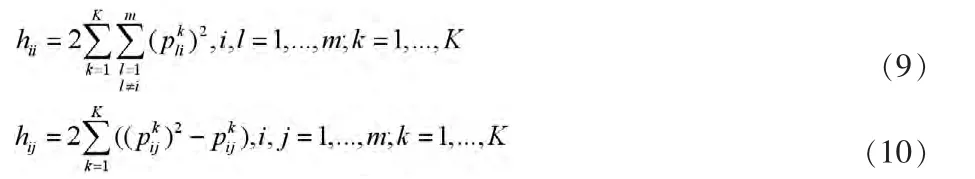
3 算例分析

4 結束語

本文提出了一種新的方法來研究不確定偏好信息的多屬性群決策問題，通過建立模型來評估各方案的排序值。在這種方法中，將多名決策者給出的不同形式的偏好信息分別規(guī)范化為模糊偏好關系，然后采用優(yōu)化模型來評估相應的排序值，即排序值越大，方案越優(yōu)。該方法具有創(chuàng)新性，同時豐富了當前解決多屬性群決策問題的解決方法，具有實際意義。

［1］陳廷.決策分析[M].北京：科學出版社,1987：1-120.

［2］Chiclana F,Herrera F,Herrera-Viedma E.Integrating three representation models in fuzzy multipurpose decision making based on fuzzy preference relations[J].Fuzzy Sets and Systems,1998,97：33-48

［3］Delgado M,Herrera F,Herrera-Viedma E,et al.Combining numerical and linguistic information in group decision making[J].Information Sciences,1998,107：177-194.

［4］王欣榮,樊治平.一種具有不同形式偏好信息的群決策方法[J].東北大學學報：自然科學版,2003,24（2）.

［5］S.J.Chen and C.L.Hwang,Fuzzy Multiple Attribute Decision Making：Methods and Applications,Springer-Verlag,New York,1992[Z].

［6］張全.復雜多準則決策應用實務[M].遼寧科學技術出版社,沈陽：2011,11.

［7］樊治平,姜艷萍,肖四漢.基于OWA算子的不同形式評好信息的群決策方法[J].控制與決策,2001,16.

［8］Ma J,Fan Z P,Huang L H.A Subjective and objective integrated approach to determine attribute weights[J].European Journal of Operational Research,1999,112(2)：397-404.