突然啟動(dòng)流動(dòng)問題:從不可壓到高超聲速流動(dòng)

吳子牛*,白晨媛徐珊妹,李娟林景陳梓鈞姚瑤

1.清華大學(xué) 航天航空學(xué)院,北京 100084 2.北京宇航系統(tǒng)工程研究所,北京 100076

翼型到達(dá)定常流動(dòng)狀態(tài)后,在無黏近似下其升力滿足儒科夫斯基升力定理,在薄翼情況下其升力系數(shù)正比于迎角[1]。實(shí)際上翼型是通過加速達(dá)到勻速運(yùn)動(dòng)狀態(tài)的。如果把加速時(shí)間看成無限小,那么就是突然啟動(dòng)問題。昆蟲撲翼在每個(gè)拍動(dòng)周期都有突然啟動(dòng)和突然停止的過程。突然啟動(dòng)問題在低速撲翼和可壓縮流動(dòng)氣動(dòng)彈性問題中有廣泛的研究[2]。

針對(duì)不可壓縮流動(dòng)問題,Wagner首次用理論研究了小迎角突然啟動(dòng)問題[3],得出了升力系數(shù)從定常升力系數(shù)的一半逐漸增加到定常值的結(jié)論。該項(xiàng)基于無黏流理論得出的結(jié)論得到了考慮黏性的實(shí)驗(yàn)驗(yàn)證[4]。在小迎角突然啟動(dòng)過程,從尾緣拖出一個(gè)近似沿直線傳播的渦層。在大迎角下,人們發(fā)現(xiàn)從尾緣脫落的渦,剛開始會(huì)卷曲成螺旋形狀,從而導(dǎo)致初始升力有奇異性[5-6]。對(duì)于平板這樣的具有尖前緣的翼型,在大迎角下,前緣也出現(xiàn)渦分離。對(duì)于這類突然啟動(dòng)問題,實(shí)驗(yàn)和數(shù)值計(jì)算[7-9]表明,除了前述升力初始奇性和 Wagner升力上升現(xiàn)象,還存在升力二次下降現(xiàn)象。對(duì)于小迎角突然啟動(dòng)問題,理論能給出全時(shí)間過程的升力特性預(yù)測(cè)[3]。對(duì)于大迎角突然啟動(dòng)問題,理論只能給出小時(shí)間的預(yù)測(cè)[6,10]。最近,Li和Wu[11]導(dǎo)出了可以針對(duì)全時(shí)間大迎角突然啟動(dòng)問題的分析方法,尤其給出了可以確定任意位置渦對(duì)升力貢獻(xiàn)的渦升力地圖。

對(duì)于可壓縮流動(dòng)問題,人們?yōu)榱搜芯繗鈩?dòng)彈性,發(fā)展了小迎角下的突然啟動(dòng)問題分析方法[12-21]。平板突然小迎角啟動(dòng)時(shí),在迎風(fēng)面和背風(fēng)面分別產(chǎn)生的壓縮波和膨脹波是小擾動(dòng)簡(jiǎn)單波,引起的壓力和在平板上的初始升力有標(biāo)準(zhǔn)的活塞理論[12-14]。隨著時(shí)間推移,這種壓力波影響會(huì)快速衰減。這方面的作用也稱為升力的無旋效應(yīng)。同時(shí),類似于不可壓縮突然啟動(dòng)問題,也存在環(huán)量建立和Wagner升力上升現(xiàn)象,只是這種現(xiàn)象有可壓縮性修正。在一定的假設(shè)下,Lomax[15]等給出了導(dǎo)出階躍函數(shù)的方法,但針對(duì)每個(gè)馬赫數(shù)其具體表達(dá)式需要單獨(dú)推導(dǎo)；后來人們發(fā)展了許多近似方法[16-21]。

依據(jù)現(xiàn)有研究結(jié)果,發(fā)現(xiàn)不可壓縮和可壓縮突然啟動(dòng)問題研究方法相對(duì)獨(dú)立,缺乏二者之間聯(lián)系的分析。對(duì)于可壓縮流動(dòng)尤其是高超聲速流動(dòng)問題[22],在大迎角下,似乎沒有突然啟動(dòng)問題報(bào)道。為了統(tǒng)一二者之間的關(guān)系,需要對(duì)二者現(xiàn)有研究現(xiàn)狀進(jìn)行綜合介紹,并指出二者之間的關(guān)聯(lián)和遺留的問題。為此,本文對(duì)不可壓縮和可壓縮突然啟動(dòng)問題涉及的現(xiàn)象和發(fā)展的研究方法進(jìn)行綜述,介紹現(xiàn)有發(fā)展動(dòng)態(tài),并指出需要進(jìn)一步研究的問題。

1 不可壓縮突然啟動(dòng)問題主要流動(dòng)現(xiàn)象

如圖1所示,在小迎角(Ao A)突然啟動(dòng)過程,從尾緣拖出一個(gè)近似沿直線傳播的渦層。渦層總的強(qiáng)度與平板內(nèi)部總的渦量合起來滿足開爾文渦量守恒定理。在大迎角下,人們發(fā)現(xiàn)從尾緣脫落的渦,剛開始會(huì)卷曲成螺旋形狀[5],并且導(dǎo)致無黏升力系數(shù)曲線初始奇性,即在零時(shí)刻,升力系數(shù)為無窮大[6]。這是因?yàn)?大迎角突然啟動(dòng)時(shí),尾部渦層首先為螺旋,外部渦量貼近尾緣上部,誘導(dǎo)的環(huán)量的初始時(shí)間變化率為無窮大,而對(duì)于非定常問題,升力系數(shù)與環(huán)量的時(shí)間變化率是成比例的。升力系數(shù)由無窮大快速下降,達(dá)到極低值后,接著遵循Wagner升力演化曲線逐漸增加。

圖1 在小迎角(Ao A)下,尾緣渦層為平面；在大迎角下尾緣渦層為螺旋[6]Fig.1 Vortex sheet is in a quasi-planar shape at small angle of attack(Ao A)and in a spiral shape at large Ao A[6]

對(duì)于平板這樣的具有尖前緣的翼型,在大迎角下,前緣也出現(xiàn)渦分離(見圖2[7])。前緣分離產(chǎn)生的前緣渦一方面會(huì)增強(qiáng)升力,另一方面,前緣渦移動(dòng)到尾緣附近后,會(huì)誘導(dǎo)新的尾緣渦,使得升力系數(shù)出現(xiàn)非定常脈動(dòng)。圖3給出了升力系數(shù)隨時(shí)間演化與典型時(shí)刻流線圖[11]。升力系數(shù)遵循如下規(guī)律:①起始過程的升力下降(圖3中的ab段)來源于初始奇性的逐漸消失；②升力系數(shù)第一次上升(圖3中bd段)來源于尾渦的脫落與附著渦的建立,同時(shí)因?yàn)榍熬墱u,該段升力系數(shù)高于Wagner模型的升力系數(shù)；③升力系數(shù)的再次下降(圖3中ei段)主要來源于新的集中尾渦出現(xiàn),該集中尾渦來源于脫落的前緣渦平移到尾緣附近時(shí)的誘導(dǎo)作用,且運(yùn)動(dòng)指向升力減小的方向。升力系數(shù)的這種震蕩會(huì)不斷循環(huán),導(dǎo)致一系列的峰值出現(xiàn)。

圖2 在15°迎角時(shí),加速運(yùn)動(dòng)平板前的前緣渦(LEV)與尾緣(TE)渦[7]Fig.2 Leading edge vortex(LEV)and trailing edge(TE)vortex for an accelerating plate at an Ao A equal to 15°[7]

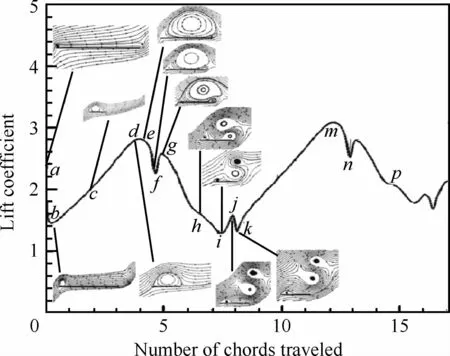
圖3 迎角20°時(shí)突然啟動(dòng)平板的升力系數(shù)演化與典型位置的流線[11]Fig.3 Time-dependent evolution of lift coefficient for an impulsively starting plate at Ao A of 20°[11]

在第2節(jié)、第3節(jié)和第4節(jié)中,將分別給出小迎角和大迎角下的分析方法。為此,先介紹相關(guān)符號(hào)約定,并簡(jiǎn)要介紹旋渦的基本作用。約定翼型從靜止突然以速度V∞和迎角α向左平動(dòng)。如果將坐標(biāo)系固定在翼型上,V∞就是啟動(dòng)后從左向右的來流速度。升力L定義為垂直于翼型平動(dòng)方向也就是垂直于來流方向的力。

在無黏框架下,定常二維流動(dòng)的翼型所受的力只有升力,即垂直于運(yùn)動(dòng)方向。而在非定常情況下,這種無黏的氣動(dòng)力F有可能并不垂直于來流方向。因此,以下的內(nèi)容將嚴(yán)格說明力的進(jìn)一步定義。升力系數(shù)定義為

式中:ρ∞為遠(yuǎn)方空氣的密度。突然啟動(dòng)問題涉及的升力與流場(chǎng)結(jié)構(gòu)與時(shí)間t有關(guān)。對(duì)于小迎角問題,有時(shí)也用到升力系數(shù)斜率CLα=d CL/dα。

定義無量綱時(shí)間為

該時(shí)間等價(jià)于當(dāng)前時(shí)刻翼型以速度V∞移動(dòng)的弦長cA的個(gè)數(shù),是突然啟動(dòng)問題涉及的無量綱時(shí)間。在第5節(jié)會(huì)進(jìn)一步討論其他形式的無量綱時(shí)間。

在突然啟動(dòng)問題的非定常流場(chǎng)中,一般存在初始時(shí)刻甚至后期時(shí)刻從尾緣甚至前緣脫落的渦。雖然從嚴(yán)格意義上講,渦是連續(xù)生成的,但為了研究方便,會(huì)將連續(xù)分布的渦尤其是集中的渦量區(qū)用點(diǎn)渦表示。作為約定,某點(diǎn)渦(指標(biāo)用i)的強(qiáng)度Γi以逆時(shí)針為正,順時(shí)針為負(fù)。尾緣產(chǎn)生的渦一般為逆時(shí)針(Γi＞0),前緣產(chǎn)生的渦一般為順時(shí)針(Γi＜0)。繞翼型的環(huán)量也是按這種符號(hào)約定。

將點(diǎn)渦的序號(hào)記為i=1,2,…,各點(diǎn)渦的坐標(biāo)記為(xi,yi)。它們?cè)诹鲌?chǎng)中任意一點(diǎn)(x,y)誘導(dǎo)的速度為

式中:ri=為點(diǎn)渦i與當(dāng)前位置的距離。根據(jù)Bai等[23],流場(chǎng)內(nèi)部的點(diǎn)渦以及翼型內(nèi)部的鏡像渦引起的單位展長上的升力可以表示為

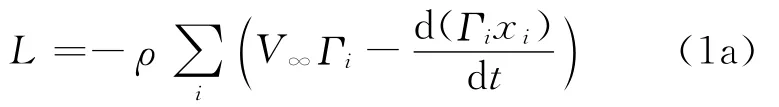
這里每個(gè)求和項(xiàng)都是針對(duì)物體內(nèi)部和外部所有的點(diǎn)渦求和并且必須假設(shè)Kelvin定理滿足,即系統(tǒng)中(包括流場(chǎng)內(nèi)部和翼型內(nèi)部)的點(diǎn)渦的總的環(huán)量為

對(duì)于連續(xù)分布的點(diǎn)渦,可以將式(1a)寫成積分形式[24]:

式中:ω=ω(x,y)為渦量分布函數(shù),可以用Dirac函數(shù)與點(diǎn)渦強(qiáng)度關(guān)聯(lián)。式(1)右端第1項(xiàng)就是定常流動(dòng)的升力,即由儒科夫斯基升力定理:

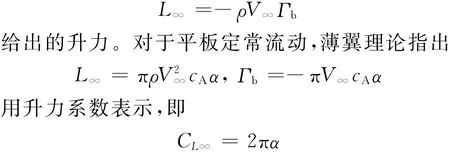
文獻(xiàn)[23]和文獻(xiàn)[24]從式(1)出發(fā),還給出了多物體流場(chǎng)中單個(gè)物體的力的表達(dá)式。

對(duì)于突然啟動(dòng)問題,在達(dá)到定常狀態(tài)之前,環(huán)量Γb是一個(gè)逐漸建立的過程,并且前緣和尾緣發(fā)出的渦會(huì)通過式(1)的右端第2項(xiàng)改變升力。到底是增加升力還是減小升力?并且,升力如何隨時(shí)間演化?這些演化與外部點(diǎn)渦的關(guān)系是什么?這些問題是突然啟動(dòng)問題需要考慮的。

2 小迎角不可壓縮問題:經(jīng)典Wagner問題

2.1 Wagner問題經(jīng)典解

如圖4所示,平板在小迎角下突然啟動(dòng)后,在尾緣會(huì)拖出渦層。同時(shí),繞平板逐漸建立環(huán)量Γb。如果用渦量分布函數(shù)來描述繞平板的環(huán)量和渦層強(qiáng)度,那么可以在平板上布置連續(xù)分布的強(qiáng)度為γ(x)的點(diǎn)渦,在渦層上布置強(qiáng)度為k(s,t)的點(diǎn)渦。

設(shè)s為從尾緣開始沿著渦層切向的距離。作為小迎角下滿足的近似,令渦層內(nèi)部沒有相互誘導(dǎo),并且在當(dāng)?shù)氐牧魉俳频扔趤砹魉俣取Ｓ谑?渦層分布在直線段0＜s＜V∞t上并且滿足渦強(qiáng)質(zhì)點(diǎn)導(dǎo)數(shù)為0(開爾文渦強(qiáng)守恒定理)的條件:

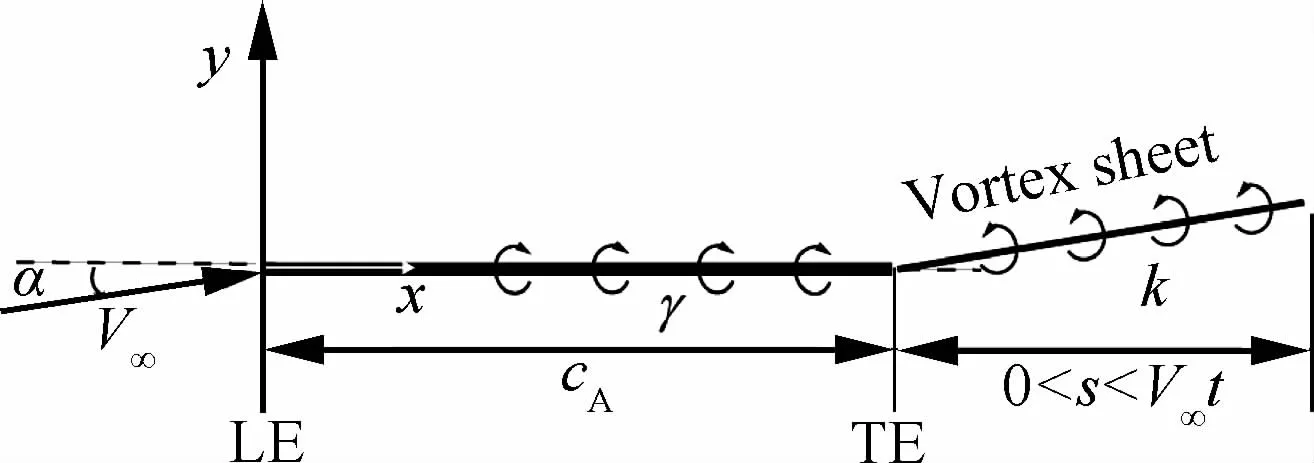
圖4 平板小迎角突然啟動(dòng)后的渦分布Fig.4 Vortex distribution for an impulsively starting plate at small Ao A

按照開爾文總渦量守恒定理,平板內(nèi)的總渦量與尾渦渦層的總渦量合起來等于0,于是

在時(shí)刻t外部存在一段分布在0＜s＜V∞t的渦層,其在平板上的誘導(dǎo)速度被平板上的點(diǎn)渦誘導(dǎo)速度平衡,利用薄翼理論不難證明,這樣的平衡關(guān)系給出[23]

從以上兩個(gè)式子消去Γb,便得到如下確定k(s,t)的方程:

該方程的解沒有解析表達(dá)式,但Wagner[3]給出了數(shù)值解。文獻(xiàn)[11]給出了如下擬合表達(dá)式:

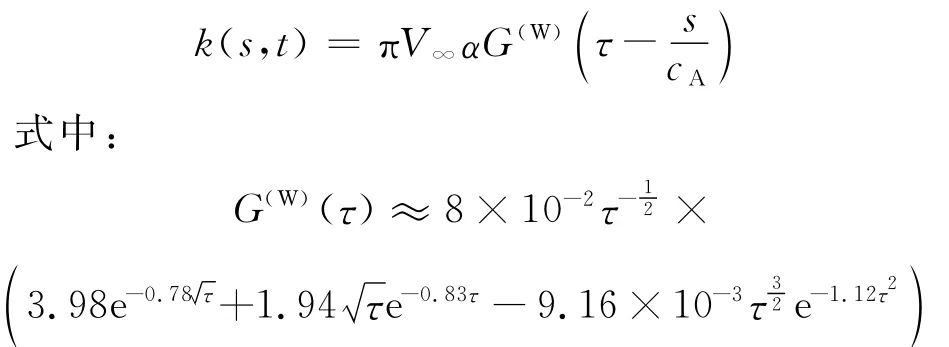
有了k(s,t),按式(2)就可以得到環(huán)量表達(dá)式Γb=-πcAV∞αF(W)(τ)。這里F(τ)稱為環(huán)量的Wagner函數(shù)。文獻(xiàn)[11]結(jié)合現(xiàn)有的表達(dá)式擬合出

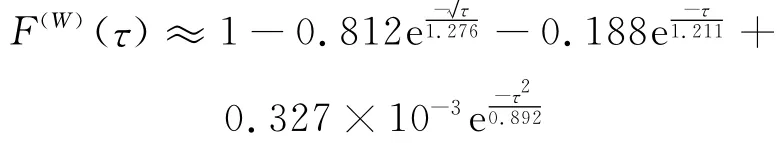
該擬合表達(dá)式滿足理論上可以證明的漸進(jìn)規(guī)律:

即在初始時(shí)刻,雖然環(huán)量為0,但其變化率為無窮大。這就導(dǎo)致初始時(shí)刻的升力系數(shù)是不為0的有限值。對(duì)于本問題,將升力的表達(dá)式(1)用到渦量沿直線分布的情況,可以將升力表示為

利用考慮了渦層影響的薄翼理論,可以求出γ的表達(dá)式,詳細(xì)表達(dá)式見文獻(xiàn)[24]。有了γ和k(s,t)的表達(dá)式后,就可以求出升力。經(jīng)過推理,該力的表達(dá)式也可以寫成[24]

但沒有解析表達(dá)式。Wagner[3]給出了如圖5所示的數(shù)值結(jié)果。

圖5 突然啟動(dòng)問題Wagner給出的原始曲線[3]Fig.5 Curves given by Wagner for impulsively starting flow[3]

為了方便使用,人們將Wagner問題的升力寫成

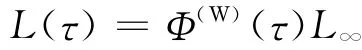
式中:L∞為定常狀態(tài)下的升力；Φ(τ)為升力的Wagner函數(shù)。人們針對(duì)Wagner函數(shù)進(jìn)行了各種擬合,其中最簡(jiǎn)單的擬合表達(dá)式為Garrick表達(dá)式:

Garrick公式誤差不到2%。Jone給出的擬合表達(dá)式為

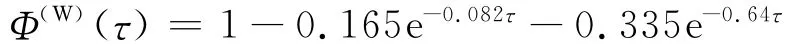
綜上所述,小迎角突然啟動(dòng)問題(Wagner問題)有如下結(jié)論:

1)初始時(shí)刻的環(huán)量為0但環(huán)量變化率為無窮大。

2)初始時(shí)刻的升力系數(shù)為定常升力系數(shù)的1/2。

3)在無量綱時(shí)間為7時(shí),升力系數(shù)達(dá)到定常升力系數(shù)的90%。

4)環(huán)量和升力隨時(shí)間沿著單調(diào)增長的Wagner函數(shù)變化。

翼型突然啟動(dòng)后,建立環(huán)量必然伴隨著旋渦從后緣脫落的過程,需一定的時(shí)間才可以完成,這就是所謂的Wagner滯后效應(yīng)。Wagner的結(jié)果可以這樣總結(jié),對(duì)于小迎角突然啟動(dòng)的薄翼,雖然附著渦的初始環(huán)量為0,但初始升力卻等于定常升力的一半。翼型的環(huán)量和升力隨著時(shí)間按Wagner函數(shù)F(τ)和Φ(τ)規(guī)律逐漸增加,在無量綱時(shí)刻等于7,即翼型移動(dòng)了7個(gè)弦長時(shí),升力達(dá)到了最終定常升力的90%。Wagner的結(jié)果在1931年被 Walker用實(shí)驗(yàn)證實(shí)[4]。

2.2 Wagner經(jīng)典問題的簡(jiǎn)化分析

當(dāng)翼型外部有點(diǎn)渦時(shí),可以簡(jiǎn)單地把翼型本身看成一個(gè)點(diǎn)渦。在這種簡(jiǎn)化處理框架下,翼型所受的升力可表示為[25]

式中:us為所有外部點(diǎn)渦(甚至包括其他物體)在翼型中點(diǎn)的誘導(dǎo)速度。文獻(xiàn)[25]用兩個(gè)集中渦分別替代附著渦和尾渦層,得到了Wagner問題的簡(jiǎn)化解析表達(dá)式。假設(shè)處在平板中心x=xb的集中附著渦渦強(qiáng)為Γb(t),處在位置x=xs的尾渦渦強(qiáng)為Γa(t)=-Γb(t)。尾渦在平板中點(diǎn)的誘導(dǎo)速度為

在該誘導(dǎo)速度修正下,平板等效迎角不等于幾何迎角。考慮到這種修正并依然使用薄翼理論,得附著渦的環(huán)量表達(dá)式為

在初始時(shí)刻,啟動(dòng)尾渦位置為xs(0)=cA,并且令該啟動(dòng)尾渦以速度d xs/d t=V∞運(yùn)動(dòng)。于是xs=cA+V∞t。將此代入式(4)可解得

式中:Γ∞=-πcAV∞α為定常流動(dòng)附著渦的環(huán)量。由于處在水平面的尾渦在平板中點(diǎn)誘導(dǎo)的水平速度近似為0,因此按式(3)得

這與Wagner的結(jié)果完全一致。

3 可壓縮小迎角問題:活塞理論與階躍函數(shù)法

3.1 初始?xì)鈩?dòng)力的活塞理論

由文獻(xiàn)[12]提出的活塞理論,可以給出在可壓縮流體中翼型小迎角突然啟動(dòng)時(shí)初始?jí)毫Ψ植己统跏忌ΑＯ然貞浺幌绿卣骶€理論中的小擾動(dòng)簡(jiǎn)單波理論。在小擾動(dòng)情況下,可壓縮流動(dòng)的某些物理量在某一區(qū)域可能是常數(shù)。其中,最典型的是黎曼不變量:

式中:下標(biāo)∞表示某參考點(diǎn)的流動(dòng)參數(shù)；V和a分別為當(dāng)?shù)亓魉俸吐曀伲沪脼楸葻岜取Ｓ稍撌娇梢越獬?/p>

由于假設(shè)是小擾動(dòng)從而是等熵流動(dòng),所以壓力可表示為

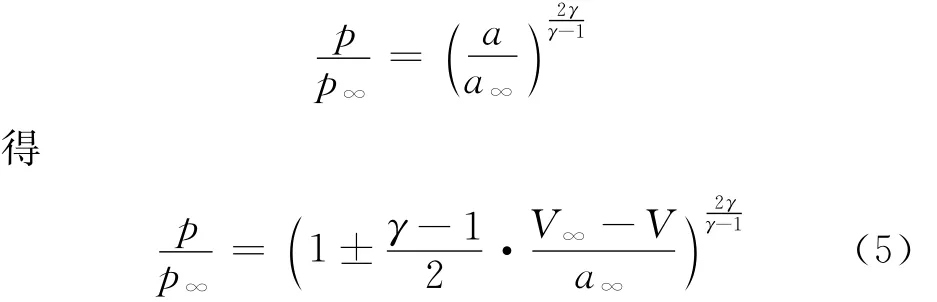
在均勻流場(chǎng)中,小擾動(dòng)導(dǎo)致的流場(chǎng),一般至少滿足其中一個(gè)這樣的關(guān)系式,這種關(guān)系稱為簡(jiǎn)單波關(guān)系。活塞理論把翼型的突然啟動(dòng)看成沿物面法向有大小等于

的小擾動(dòng)。這種小擾動(dòng)激發(fā)的流動(dòng)是簡(jiǎn)單波,從而導(dǎo)致的壓力變化,按式(5)得

針對(duì)更一般的情況,Lomax等給出了更為復(fù)雜的表達(dá)式。圖6[15]給出了Lomax等理論得到的升力系數(shù)斜率隨無量綱時(shí)間的變化曲線。在文獻(xiàn)[26]中,Bai等針對(duì)馬赫數(shù)Ma∞=0,0.5,0.8用CFD做了計(jì)算(見圖7),發(fā)現(xiàn)結(jié)果與文獻(xiàn)[15]的理論結(jié)果吻合得非常好。

其中正負(fù)號(hào)可分別用在迎風(fēng)面(增壓)和背風(fēng)面(降壓)。式(6)即為氣動(dòng)彈性問題中計(jì)算突然運(yùn)動(dòng)引起的瞬間氣動(dòng)力的活塞理論。其引起的初始時(shí)刻的法向力系數(shù)為

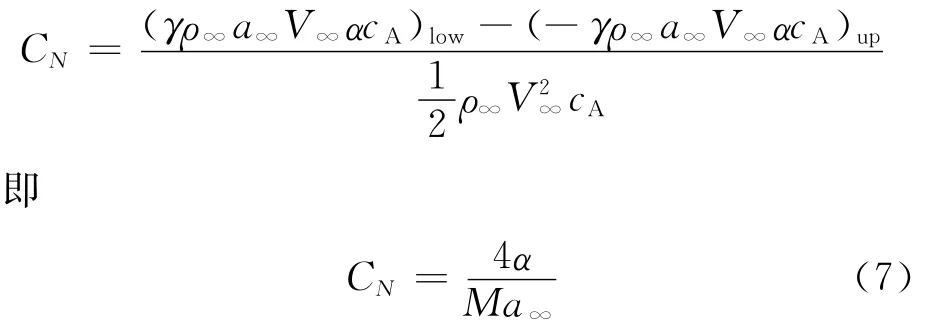
式(7)就是氣動(dòng)彈性理論中用于計(jì)算瞬間位移引起的氣動(dòng)力修正的活塞理論[12],可以用到從亞聲速到超聲速情況下的任何馬赫數(shù)[12-14]。這里Ma∞=V∞/a∞為來流馬赫數(shù)。

3.2 氣動(dòng)力演化的階躍函數(shù)法

Lomax等[15]用小擾動(dòng)線性波動(dòng)方程,給出了計(jì)算突然啟動(dòng)等問題的非定常升力計(jì)算方法,并且針對(duì)幾個(gè)特殊馬赫數(shù),給出了具體表達(dá)式和曲線。在無量綱時(shí)間滿足

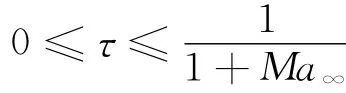
的初始階段,升力系數(shù)近似線性下降,表達(dá)式為

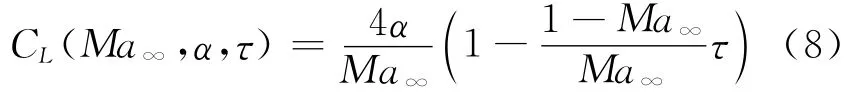
在不可壓極限情況下,針對(duì)0≤τ≤∞,升力系數(shù)由Wagner解給出

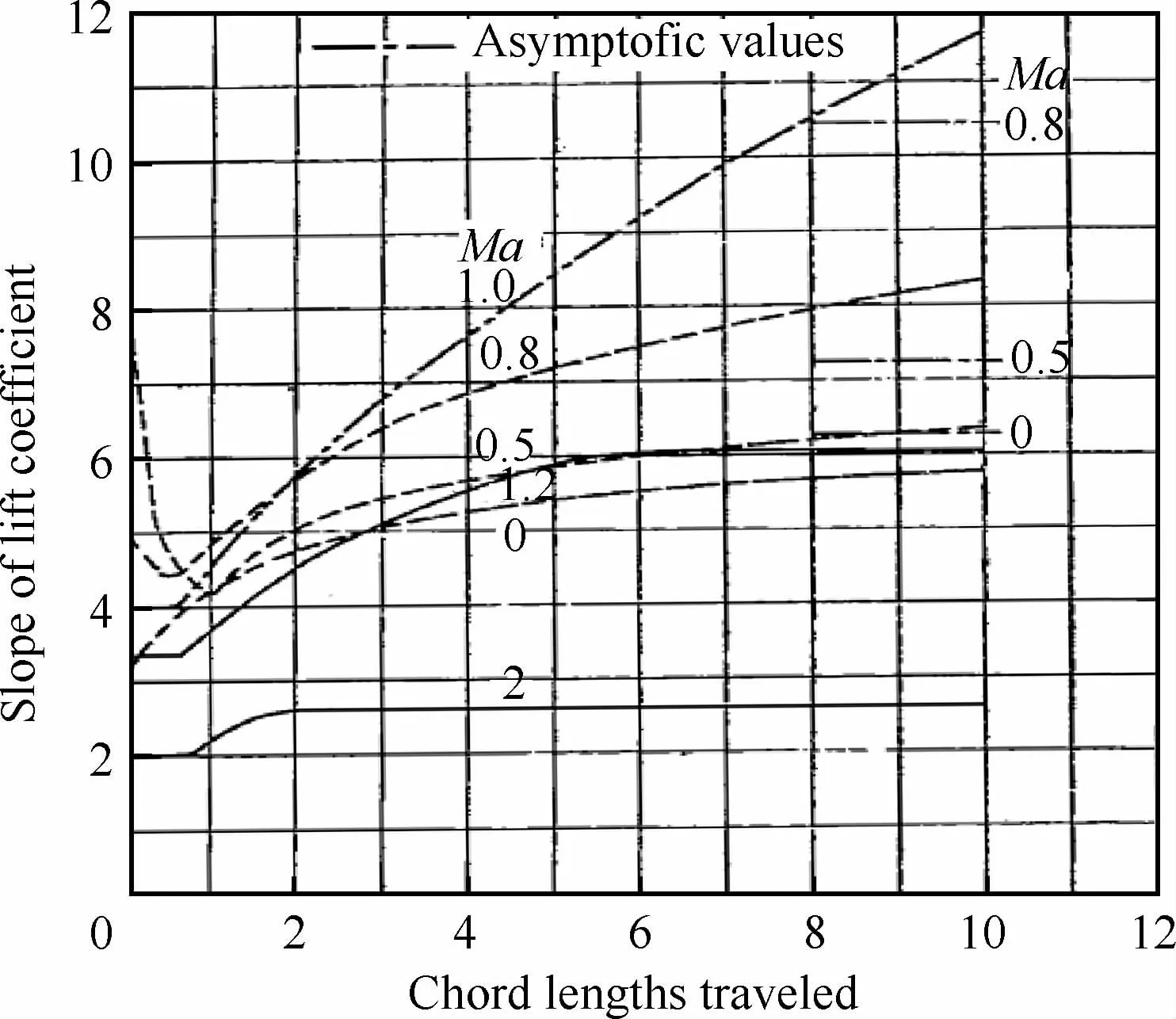
圖6 可壓縮突然啟動(dòng)問題的升力系數(shù)斜率CLα=d CL/dα隨無量綱時(shí)間的變化率[15]Fig.6 Time-dependent evolution of slope of lift coefficient CLα=d CL/dαfor compressible starting flow[15]

圖7 不同馬赫數(shù)下可壓縮突然啟動(dòng)問題的升力系數(shù)斜率CLα=d CL/dα隨無量綱時(shí)間的變化率[26]Fig.7 Time-dependent evolution of slope of lift coefficient CLα=d CL/dαfor compressible starting flow[26]at different Mach numbers

作為近似處理,對(duì)于更一般的情況,可以將升力系數(shù)寫為[16-18]

式中:Φ(I)、Φ(C)為階躍函數(shù)；β=1 - Ma2∞為普朗特-葛勞沃特(PG)可壓縮性修正因子。第一個(gè)階躍函數(shù)Φ(I)(τ)與環(huán)量無關(guān),來源于活塞效應(yīng)及其衰減(non-circulatory part)；第二個(gè)階躍函數(shù)Φ(C)與環(huán)量有關(guān),來源于流場(chǎng)中渦量場(chǎng)以及繞翼型環(huán)量的貢獻(xiàn),在不可壓縮特殊情況,就是Wagner函數(shù),即

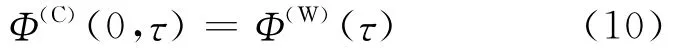
另外,在小時(shí)間步的情況下,式(9)應(yīng)退化為式(8),即

在滿足約束關(guān)系式(10)和式(11)的條件下,人們依據(jù)實(shí)驗(yàn)或數(shù)值計(jì)算結(jié)果,擬合了階躍函數(shù)的一些近似表達(dá)式。例如,Leishman[16]令

經(jīng)驗(yàn)算,發(fā)現(xiàn)這種做法對(duì)于突然啟動(dòng)問題,結(jié)果在τ=O(1)左右的誤差較大。一種改進(jìn)做法是,令

并令式(11)的各階導(dǎo)數(shù)在τ=0成立,得?(τ)滿足的幾個(gè)關(guān)系式,再將?(τ)寫成含有幾個(gè)系數(shù)的指數(shù)函數(shù),就可以通過定出這幾個(gè)系數(shù)來擬合。這個(gè)問題需要進(jìn)一步研究。

4 不可壓縮大迎角問題:修正的Wagner函數(shù)法與渦力線理論

4.1 小時(shí)間升力特性

對(duì)于小迎角下的突然啟動(dòng)問題,尾部拖出的渦層近似分布在一個(gè)平面上,而對(duì)于大迎角問題,尾部拖出的渦至少在初始時(shí)刻會(huì)卷曲成螺旋渦(見圖1)。與小迎角Wagner問題的初始升力為定常升力的一半不同,這種螺旋渦的誘導(dǎo)作用使得初始升力為無窮大。Graham證明[6],初始時(shí)刻的升力系數(shù)急劇下降,滿足關(guān)系式:

式中:k=2-?tr/π,?tr為尾緣角。對(duì)于尾緣角為0的平板,有

Pullin和Wang[10]考慮了尖前緣的情況。此時(shí),無論是尾緣還是前緣,都有螺旋渦拖出,如圖8所示。

圖8 大迎角突然啟動(dòng)與加速問題的前緣渦與尾渦[10]Fig.8 Impulsively starting flow at large Ao A having both leading and trailing edge vortices in spiral shape[10]

在時(shí)間足夠小的情況下,突然加速所受的力F垂直于平板并且平板法向力滿足

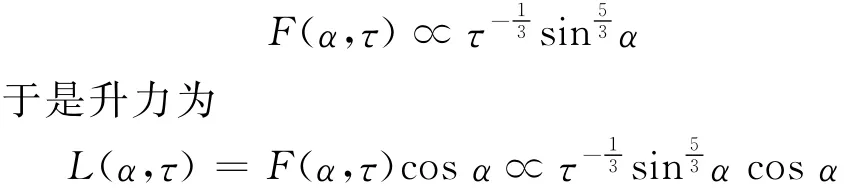
令該升力表達(dá)式對(duì)迎角的導(dǎo)數(shù)等于0,文獻(xiàn)[6]得到的最大升力系數(shù)對(duì)應(yīng)的迎角為

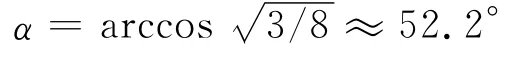
據(jù)此他們認(rèn)為昆蟲近似采用這么大的迎角飛行,以便獲得最大升力。

4.2 長時(shí)間修正的Wagner函數(shù)法

對(duì)于長時(shí)間行為,Li和Wu[11]用圖9近似真實(shí)情況,即假定有前緣渦、在時(shí)間為0＜τ＜τ0的初始階段有螺旋尾渦在尖尾緣,在時(shí)間τ0＜τ＜τ1拖出的尾渦又近似在一個(gè)平面上。

圖9 大迎角突然啟動(dòng)問題的前緣渦與尾渦[11]Fig.9 Leading edge and trailing edge vortices for starting flow at large Ao A[11]

將前緣渦和初始尾渦看成兩個(gè)或多個(gè)額外的離散渦,得到了這樣的升力表達(dá)式,即

修正的Wagner函數(shù)比原始Wagner函數(shù)小。道理很簡(jiǎn)單,因?yàn)槌跏紩r(shí)間段的尾渦被卷曲,已經(jīng)算到式(12)右端第2項(xiàng)了。在右端第2項(xiàng)中,I為額外點(diǎn)渦即附加渦的個(gè)數(shù),包括前緣渦和初始時(shí)刻的卷曲尾渦(即時(shí)間τ0＜τ＜τ1段平面渦層外的所有渦,無論是看成集中渦還是看成一系列的點(diǎn)渦)。另外,U(i)為點(diǎn)渦的移動(dòng)速度,ΛA=[PAQA]為附加渦的渦力線矢量,OA、PA和QA為附加渦升力因子,其表達(dá)式分別為

依據(jù)表達(dá)式(12)的分析表明,處在前緣附近的前緣渦(順時(shí)針)引起的附加渦升力,將原始的Wagner曲線抬高。這就是前緣渦增強(qiáng)機(jī)制的本質(zhì)原因。但是,這項(xiàng)研究表明,前緣渦遠(yuǎn)離前緣后,并不再增強(qiáng)升力。

4.3 長時(shí)間渦力線方法

表達(dá)式(12)并不能用于處理τ＞τ1的情況。此時(shí),從尾緣有其他的螺旋渦脫落出。文獻(xiàn)[11]研究表明,在迎角足夠大后,前緣集中渦一旦脫落并且移動(dòng)至尾緣附近,那么就會(huì)導(dǎo)致產(chǎn)生第二個(gè)螺旋尾渦,此時(shí)表達(dá)式(12)不能繼續(xù)使用。為了考慮更一般的情況,文獻(xiàn)[11]將所有的渦(包括可能存在的平面渦層)看成離散點(diǎn)渦。假設(shè)流場(chǎng)中一共有I這樣的離散渦,那么升力可表示為

式中:ΛB=[PBQB]為渦升力線矢量；為渦升力線角,表示速度矢量U(i)(與問題相關(guān))與渦升力矢量ΛB(與問題無關(guān))之間的夾角。這里,PB=PB(p,q)、QB=QB(p,q)均為與時(shí)間無關(guān)的總渦升力因子,定義如下:

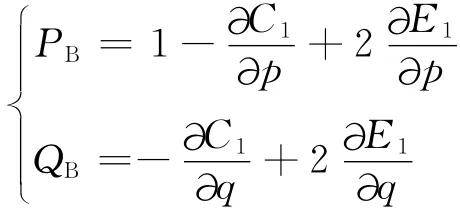
文獻(xiàn)[11]給出了用于定性分析點(diǎn)渦對(duì)升力貢獻(xiàn)的渦升力線圖(Vortex Force Line Map),文獻(xiàn)[27]對(duì)此圖進(jìn)行了修正,見圖10。

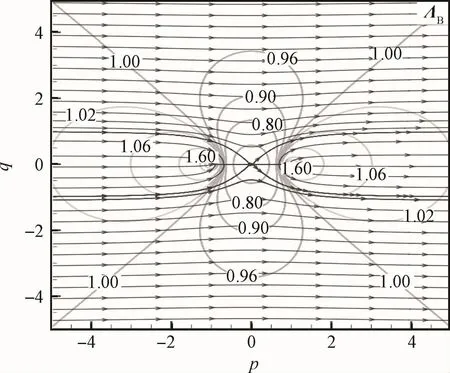
圖10 渦升力線圖[27]Fig.10 Vortex force line map[27]

圖中帶箭頭的曲線類似于流線,即將流線中的速度矢量用渦升力線矢量ΛB替代。不帶箭頭的曲線代表ΛB的等值線。在渦升力線圖中,存在一條特殊的升力線ls,在平板中間點(diǎn)x=cA/2(p=0)位置穿過平板。考慮上半部分,即q＞0的區(qū)域,ls左側(cè)的總升力線在平板前緣處匯聚成一點(diǎn),而ls右側(cè)的總升力線在平板尾緣處匯聚成一點(diǎn)。文獻(xiàn)[11]還有另外一條臨界線,標(biāo)記為lm,此處ΛB≈0.707,經(jīng)過驗(yàn)證,其實(shí)不存在這條臨界線。ΛB在靠近前緣的地方很大(前緣敏感區(qū)),在靠近尾緣的地方也會(huì)變大(尾緣敏感區(qū)),在尾緣點(diǎn)處ΛB的值無窮大。當(dāng)渦進(jìn)入這些敏感區(qū)的時(shí)候會(huì)誘導(dǎo)出很大的升力或者是升力的變化。這就是為什么初始時(shí)刻螺旋尾渦產(chǎn)生時(shí),升力為無窮大并且快速下降的原因。依據(jù)表達(dá)式(13)并結(jié)合圖10,有如下結(jié)論[11]:

文獻(xiàn)[11]正是基于這種方法,用基于離散渦模擬或CFD模擬得到渦場(chǎng)后,解釋了大迎角下各種升力下降、上升與再次下降的詳細(xì)過程。其中一個(gè)重要結(jié)果是,對(duì)于20°迎角平板突然啟動(dòng)問題,前緣渦脫落移動(dòng)到尾緣附近(按圖10,導(dǎo)致升力下降),會(huì)誘導(dǎo)出一個(gè)螺旋渦臨時(shí)向上游移動(dòng)(按圖10,進(jìn)一步導(dǎo)致升力下降),導(dǎo)致升力系數(shù)有大幅度的下降(見圖3)。這就是固定翼飛行很難采用大迎角的原因。文獻(xiàn)[10]只給出了20°迎角的計(jì)算結(jié)果分析；文獻(xiàn)[27]推廣到了更高迎角的情況。依據(jù)文獻(xiàn)[27]的結(jié)果,對(duì)于更高迎角,渦力線模型(式(13))能較為準(zhǔn)確地預(yù)測(cè)平板所受的法向力。

5 結(jié)果討論與存在的問題

以平板翼型為例,突然啟動(dòng)問題的現(xiàn)有研究可以總結(jié)如下:

1)小迎角不可壓縮突然啟動(dòng)問題。尾部連續(xù)拖出渦,渦層近似為平面形狀；針對(duì)所有時(shí)刻有精確解但升力系數(shù)和環(huán)量隨無量綱時(shí)間τ=V∞t/cA的演化規(guī)律只能給出擬合表達(dá)式。初始升力等于定常升力的1/2,這來源于初始時(shí)刻環(huán)量的變化率(環(huán)量變化率也貢獻(xiàn)升力),雖然初始時(shí)刻的環(huán)量為0。在翼型移動(dòng)7個(gè)弦長的距離(即τ=7)后,升力系數(shù)為定常升力系數(shù)的90%。

2)小迎角可壓縮問題。初始時(shí)刻有壓縮和膨脹小擾動(dòng)波分別在迎風(fēng)面和背風(fēng)面產(chǎn)生；其法向流動(dòng)可按一維活塞理論處理；這種小擾動(dòng)波的產(chǎn)生導(dǎo)致初始升力系數(shù)反比于馬赫數(shù)(CL(0)=4αMa)；隨著時(shí)間推移,類似于不可壓情況的環(huán)量的建立,導(dǎo)致升力系數(shù)先近似線性變化(亞聲速時(shí)線性下降,超聲速時(shí)可能線性上升),接著逐漸上升,最后趨向于定常解(即儒科夫斯基升力定理加上普朗特-葛勞沃特可壓縮性修正)。在一些文獻(xiàn)上,活塞效應(yīng)及其衰減以及環(huán)量效應(yīng)被分成兩部分單獨(dú)處理,并采用不同的擬合函數(shù)(階躍函數(shù))。

圖11 升力系數(shù)隨時(shí)間的演化[26]Fig.11 Time-dependent evolution of lift coefficient[26]

3)不可壓縮大迎角問題。在初始時(shí)刻,尖尾緣有螺旋渦產(chǎn)生,導(dǎo)致初始升力系數(shù)為無窮大并隨時(shí)間推移快速衰減；當(dāng)這個(gè)螺旋尾渦脫落后,新拖出的渦近似可以看成平面渦層(與小迎角時(shí)類似),升力系數(shù)隨時(shí)間逐漸增加；如果是尖前緣,那么尖前緣處也有渦脫落；前緣渦在前緣附近時(shí),使得升力系數(shù)曲線高于經(jīng)典 Wagner曲線,如果前緣渦移動(dòng)到尾緣附近,則引起升力下降,進(jìn)一步如果誘導(dǎo)出新的尾渦,那么升力系數(shù)會(huì)急劇下降；文獻(xiàn)[10]提出的渦升力線圖能用于有效刻畫點(diǎn)渦對(duì)升力變化的貢獻(xiàn)。

平板以外的翼型以及黏性等對(duì)上述結(jié)果有定量修正但定性結(jié)果依然成立。從現(xiàn)有文獻(xiàn)可以看出,可壓縮大迎角突然啟動(dòng)問題,缺乏分析理論和結(jié)果。在文獻(xiàn)[26]中,Bai等針對(duì)馬赫數(shù)Ma∞=0.5,0.8,0.9用CFD做了20°迎角時(shí)的計(jì)算,發(fā)現(xiàn)結(jié)果與圖3那樣的不可壓縮流動(dòng)結(jié)果相比有一定的相似性。其中針對(duì)亞聲速突然啟動(dòng)問題的一條重要結(jié)論是,在升力系數(shù)上升的起始階段,馬赫數(shù)越高升力系數(shù)越小,這與可壓縮性效應(yīng)提高升力系數(shù)有矛盾,因此需要進(jìn)一步研究。文獻(xiàn)[26]也計(jì)算了馬赫數(shù)為1.5時(shí)的超聲速大迎角突然啟動(dòng)問題,如圖11(a)所示。可見,在這種條件下,升力系數(shù)不像亞聲速那樣有震蕩,而是比較單調(diào)地變化。原因在于,在這樣的條件下,沒有明顯的渦脫落。

圖11(b)給出了高超聲速條件下(Ma∞=8.0)平板大迎角突然啟動(dòng)問題的升力系數(shù)。發(fā)現(xiàn),在極短的時(shí)間內(nèi),即達(dá)到定常解。但是,在初始時(shí)刻,升力系數(shù)先急劇上升,達(dá)到某個(gè)峰值,再急劇下降。這一結(jié)果與圖11(a)所示的低超聲速結(jié)果有明顯差異,具體原因有待進(jìn)一步分析。

4)特征時(shí)間。對(duì)于突然啟動(dòng)問題,人們一直采用特征時(shí)間τ,但圖6、圖7和圖11表明,升力系數(shù)演化的第一階段(近似線性階段)的結(jié)束時(shí)刻τ似乎與馬赫數(shù)Ma∞有關(guān)系。為此我們定義三個(gè)無量綱時(shí)間,即基于波速的無量綱時(shí)間:

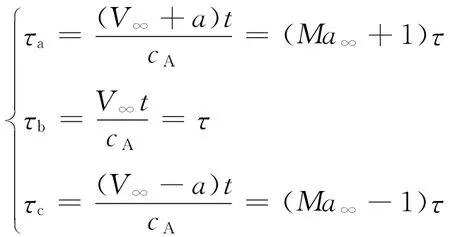
它們分別是最快運(yùn)動(dòng)的小擾動(dòng)波在當(dāng)前時(shí)刻移動(dòng)的弦長個(gè)數(shù),以對(duì)流速度運(yùn)動(dòng)的小擾動(dòng)波在當(dāng)前時(shí)刻移動(dòng)的弦長個(gè)數(shù)和最慢運(yùn)動(dòng)的小擾動(dòng)波當(dāng)前時(shí)刻移動(dòng)的現(xiàn)象個(gè)數(shù)。這里,λ1=V∞+a是第三簡(jiǎn)單波對(duì)應(yīng)的速度(特征值),λ2=V∞是對(duì)流速度,λ3=V∞-a是第一簡(jiǎn)單波對(duì)應(yīng)的速度(特征值)。流動(dòng)特性與升力曲線演化特性與這三個(gè)特征時(shí)間的具體關(guān)系,需要進(jìn)一步研究。

實(shí)際應(yīng)用很難做到真正的突然啟動(dòng),即翼型或機(jī)翼很難瞬間獲得最終速度(否則意味著初始時(shí)刻的加速度是無窮大),而是需要一個(gè)初始加速過程。此時(shí)V∞=V∞(t)。這一加速過程帶來兩個(gè)方面的影響:

1)附加慣性力。附加慣性力與加速度成正比,處理方法見文獻(xiàn)[7,9,10,23]以及其中引用的參考文獻(xiàn)。例如,平板的附加慣性導(dǎo)致的升力為

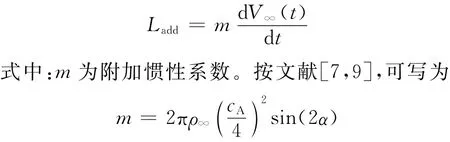
2)歷史效應(yīng)。文獻(xiàn)[10]將 Wagner經(jīng)典理論用于加速平板時(shí),針對(duì)每一時(shí)刻的當(dāng)前速度,直接套用原始Wagner公式。在文獻(xiàn)[7,9]中,也并沒有考慮加速過程歷史效應(yīng)的累計(jì)影響。但在氣動(dòng)彈性階躍函數(shù)研究中,歷史效應(yīng)用Duhamel法則[17,28-29]計(jì)入(卻不計(jì)入附加慣性力)。例如,對(duì)于小迎角不可壓縮任意運(yùn)動(dòng)問題:

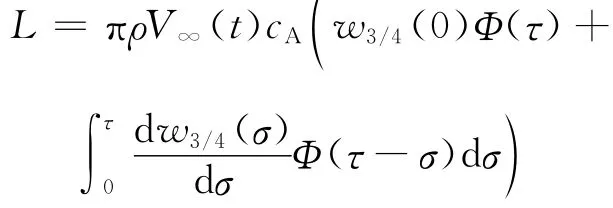
式中:w3/4=w3/4(τ)為3/4弦長處的下洗速度。對(duì)于定常問題,下洗速度就是來流速度被帶迎角的翼型向下折轉(zhuǎn)了速度分量。對(duì)于平板定常流動(dòng),w3/4(∞)=V∞(∞)sinα,Φ(∞)=1,因此

即退化為儒科夫斯基升力定理給出的升力。

附加慣性效應(yīng)和基于Duhamel法則的歷史效應(yīng)為何在兩類文獻(xiàn)中并不同時(shí)出現(xiàn),也是一個(gè)需要進(jìn)一步考慮的問題。

6 結(jié) 論

本文對(duì)突然啟動(dòng)問題涉及的流動(dòng)現(xiàn)象、升力演化規(guī)律和分析方法進(jìn)行了綜合介紹。過去人們將不可壓縮和可壓縮突然啟動(dòng)問題看成不同問題進(jìn)行研究,本文首次將二者進(jìn)行比較性研究。研究結(jié)果表明:

1)對(duì)于小迎角突然啟動(dòng)問題,現(xiàn)有分析方法可以給出大時(shí)間范圍中升力系數(shù)隨時(shí)間的演化曲線。在初始時(shí)刻,可壓縮與不可壓縮卻存在本質(zhì)區(qū)別,前者由小擾動(dòng)波主導(dǎo),后者由環(huán)量主導(dǎo)。

2)對(duì)于大迎角突然啟動(dòng)問題,初始時(shí)刻的升力無論對(duì)于可壓縮還是不可壓縮,都存在突然下降現(xiàn)象,但對(duì)于大時(shí)間范圍,不可壓縮流動(dòng)存在升力脈動(dòng)現(xiàn)象,對(duì)于高馬赫數(shù)可壓縮流動(dòng),脈動(dòng)現(xiàn)象明顯減弱甚至消失。

3)對(duì)于大迎角可壓縮問題,尚無理論分析方法可以給出長時(shí)間升力演化預(yù)測(cè)。一個(gè)針對(duì)高超聲速條件的計(jì)算表明,大迎角下可能存在特殊的初始升力脈動(dòng)現(xiàn)象。這一現(xiàn)象過去未見報(bào)道。

本文綜述結(jié)果對(duì)從事氣動(dòng)彈性、撲翼飛行和大迎角機(jī)動(dòng)研究具有借鑒作用。同時(shí)指出了存在的理論空白,包括大迎角可壓縮問題的理論方法尚未建立,以及高超聲速條件下存在一些升力系數(shù)脈動(dòng)現(xiàn)象。這些問題需要進(jìn)一步研究。

[1] Anderson J.McGraw-Hill series in aeronautical and aerospace engineering[M].[s.l.]:McGraw-Hill,1989.

[2] Sun M.Insect flight dynamics:stability and control[J].Reviews of Modern Physics,2014,86(2):615.

[3] Wagner H.über die Entstehung des dynamischen auftriebes von tragflügeln[J].ZAMM-Journal of Applied Mathematics and Mechanics/Zeitschrift für Angewandte Mathematik und Mechanik,1925,5(1):17-35.

[4] Walker P B.Experiments on the growth of circulation about a wing and an apparatus for measuring fluid motion[J].Rep.Memo.Aeronaut.Res.(Great Britain),1931,1402.

[5] Pullin D I.The large-scale structure of unsteady self-similar rolled-up vortex sheets[J].Journal of Fluid Mechanics,1978,88(3):401-430.

[6] Graham J M R.The lift on an aerofoil in starting flow[J].Journal of Fluid Mechanics,1983,133:413-425.

[7] Pitt Ford C W,Babinsky H.Lift and the leading-edge vortex[J].Journal of Fluid Mechanics,2013,720:280-313.

[8] Dickinson M H,Gotz K G.Unsteady aerodynamic performance of model wings at low Reynolds numbers[J].The Journal of Experimental Biology,1993,174(1):45-64.

[9] Xia X,Mohseni K.Lift evaluation of a two-dimensional pitching flat plate[J].Physics of Fluids(1994-present),2013,25(9):091901.

[10] Pullin D I,Wang Z.Unsteady forces on an accelerating plate and application to hovering insect flight[J].Journal of Fluid Mechanics,2004,509:1-21.

[11] Li J,Wu Z N.Unsteadylift for the wagner problem in the presence of additional leading/trailing edge vortices[J].Journal of Fluid Mechanics,2015,769:182-217.

[12] Ashley H,Zartarian G.Piston theory-a new aerodynamic tool for the aeroelastician[J].Journal of the Aeronautical Sciences(Institute of the Aeronautical Sciences),1956,23(12):1109-1118.

[13] Liu D D,Yao Z X,Sarhaddi D,et al.From piston theory to a unified hypersonic-supersonic lifting surface method[J].Journal of Aircraft,1997,34(3):304-312.

[14] Oppenheimer M W,Skujins T,Bolender M A,et al.A flexible hypersonic vehicle model developed with piston theory,AIAA-2007-6396[R].Reston:AIAA,2007.

[15] Lomax H,Heaslet M A,Fuller F B,et al.Two-and three-dimensional unsteady lift problems in high-speed flight,NAGA 1077[R].Washington,D.C.:NACA,1952.

[16] Leishman J G.Validation of approximate indicial aerodynamic functions for two-dimensional subsonic flow[J].Journal of Aircraft,1988,25(10):914-922.

[17] Leishman J G.Indicial lift approximations for two-dimensional subsonic flow as obtained from oscillatory measurements[J].Journal of Aircraft,1993,30(3):340-351.

[18] Leishman J G.Unsteady lift of a flapped airfoil by indicial concepts[J].Journal of Aircraft,1994,31(2):288-297.

[19] Hariharan N,Leishman J G.Unsteady aerodynamics of a flapped airfoil in subsonic flow by indicial concepts[J].Journal of Aircraft,1996,33(5):855-868.

[20] Sitaraman J,Baeder J D.Computational-fluid-dynamicsbased enhanced indicial aerodynamic models[J].Journal of Aircraft,2004,41(4):798-810.

[21] Jose A I,Leishman J G,Baeder J D.Unsteady aerodynamic modeling with time-varying free-stream mach numbers[J].Journal of The American Helicopter Society,2006,51(4):299-318.

[22] Wu Z N,Bai C Y,Li J,et al.Analysis of flow characteristics for hypersonic vehicle[J].Acta Aeronautica et Astronautica Sinica,2015,36(1):58-85(in Chinese).吳子牛,白晨媛,李娟,等.高超聲速飛行器流動(dòng)特征分析[J].航空學(xué)報(bào),2015,36(1):58-85.

[23] Bai C Y,Li J,Wu Z N.Generalized Kutta-Joukowski theorem for multi-vortex and multi-airfoil flow with vortex production—A general model[J].Chinese Journal of Aeronautics,2014,27(5):1037-1050.

[24] Li J,Wu Z N.A two-dimensional multibody integral approach for forces in inviscid flow with free vortices and vortex production[J].Journal of Fluids Engineering,2015,137(021205-1).

[25] Bai C Y,Wu Z N.Generalized Kutta-Joukowski theorem for multi-vortices and multi-airfoil flow(alumped vortex model)[J].Chinese Journal of Aeronautics,2014,27(1):34-39.

[26] Bai C Y,Li J,Wu Z N.Unsteady lift for impulsively started transonic/supersonic flow[C]//Proceedings of The ASME 2015 International Mechanical Engineering Congress&Exposition.to appear in,2015.

[27] Li J,Bai C Y,Wu Z N.Unsteady lift for the wagner problem of starting flow at large angle of attack[C]//Proceedings of The ASME 2015 International Mechanical Engineering Congress&Exposition.to appear in,2015.

[28] Gaunaa M,Bergami L,Heinz J.Indicial response function for finite-thickness airfoils,a semi-empirical approach,AIAA-2011-0542[R].Reston:AIAA,2011.

[29] Bisplinghoff R L,Ashley H,Halfman R L.Aeroelasticity[M].[s.l.]:Dover Publications,Inc,1996.