集合材料在音樂中的結構關系

廖軻

【摘要】作為二十世紀最重要的作曲家之一，勛伯格打破了傳統音樂的調性束縛，促進了無調性音樂的發展，他的鋼琴代表作之一《鋼琴小品六首》也被后人作為無調性的代表作品而廣泛分析與研究。本文就以《鋼琴小品六首》op.19no.3為例，運用集合理論進行音樂材料的結構分析，從而探索出集合材料在該音樂作品中的內在結構關系，并發掘出其在如何推動音樂的發展中所起到的重要地位。

【關鍵詞】音級集合；截斷；集合材料；結構關系

引言

奧地利作曲家、理論家和音樂教育家阿諾德·勛伯格（ArnoldSchoenberg）是二十世紀以來最具影響力的一位音樂大師，其對當代音樂的貢獻使得他在音樂史上占有著重要的位置。占有重要地位的傳統調性音樂統治著音樂界長達幾個世紀之久。然而這一情形被勛伯格最早打破，他擺脫了傳統調性音樂的束縛并開啟了無調性音樂時期，后來經過不斷了探索，他創造性的提出了十二音序列音樂寫作的模式，并以此為理論依據創作了大量音樂作品。然而從調性音樂劍無調性音樂的發展，這個改變的過程并非一帆風順，在這個過程巾，勛伯格不斷的打破傳統音樂的理論束縛，不儀在和聲上還是在曲式結構等方面，可以說勛伯格完全是在顛覆傳統音樂的理論理念。但經過不斷的摸索，勛伯格最終找到r適合自己的一套音樂體系，他的努力也成功的使他在音樂史上占有一席之地，為音樂理論的發展做出r巨大的貢獻。《鋼琴小品六首》op.19則是勛伯格的代表作品之一，而本文分析的是其中第二首，分析的方法采用的是音級集合理論，運用這一理論可以發掘音樂內在的結構關系，從而更為客觀的分析出音樂的材料運用和音樂的整體與細微之問的聯系。集合理論作為現代音樂的一種分析手段，最早由美國理論家彌爾頓·巴比特（Milton Bahhitt）提出，在二十世紀初開始形成，經過艾倫·福特（Allen Forte）的總結發展，漸漸成為了一套較為全面的理論體系，不過集合理論的發展遠未停止，許多音樂理論家不斷探索和研究，豐富著集合理論體系。

一、《鋼琴小品六首》op.19 no.2的集合材料

用集合的方法分析作品結構，第一步首先要劃分出音樂作品的材料結構塊，即集合理論中所說的截斷，從該作品的旋律線以及音樂段落的結構上看，我們可以劃分出8個截段材料。然后把這8個截斷材料從整首作品巾分離并依序表示出來，如圖1所示。

二、各截斷的集合

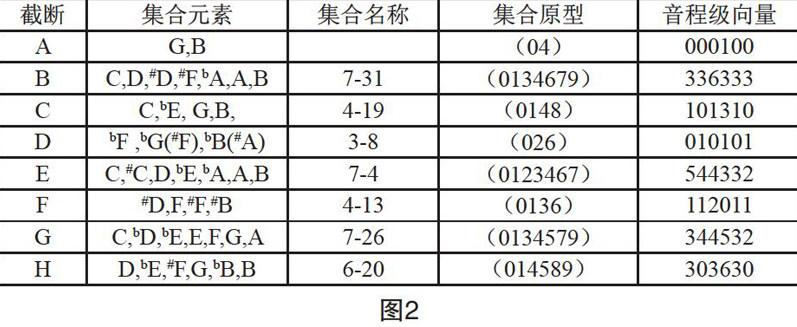
通過把各個截斷從整首作品中截取出來，我們便得到了類似于樂匯般的諸多音樂材料片段，這些片段及其一些發展和變化共同構成了這首完整的作品。接下來我們便是需要探尋這些截斷材料其本身的內涵與相互之問的內在關系。運用集合理論與集合族列表，能夠得到每個截斷具體的集合，如圖2所示。

三、各截斷在音樂整體中的結構關系

透過上面的截斷集合列表，我們能夠了解每個截斷的集合內容，包括集合原型以及音程級向量等。把所有截斷都截取出來后我們能夠觀察每個截斷的自身關系與特點，但在分析的過程巾每個材料都不是單獨存在的，通過每個材料與全曲之問關系的分析和每個材料相互之問的關系的分析，才能使我們對于整部作品的結構框架以及音樂表現的內容有所了解，首先是把截斷還原于樂曲本來的位置進行解釋分析。

樂曲的一開始出現的是截斷A的集合內容，截斷A是一個雙音級合，由于在艾倫·福特的集合表里標記出的最小集合為二音級合，因此，截斷A的雙音級合并沒有集合名稱（也稱為福特名）。但是按照音程級向量的計算方式依然可以將雙音級合的音程級向量算出，縱觀全曲，音樂的發展基于截斷A中的雙音級合，一直到樂曲結束；截斷B是一個七音級合，連音線使得這幾個音成劃分為—個整體，這個截斷的音樂形態在全曲中是一個具有旋律特線征的集合；截斷C是四音級合，是包含截斷A中雙音級合元素的一個發展；截斷D是由—個三音和弦和一個雙音組成，按照等音相同的概念，這兩個和弦中有兩對音組的集合元素相同，因此截斷D是—個四音級合；截斷E是由四組三度關系的雙音組成的一個七音級合；截斷F為一個有延留的七音柱式和弦結構的四音級合；截斷G與截斷E相似，由五組三度關系的雙音組成，與截斷E不同之處在于節奏與音符時值的不同；截斷H同樣為一個七音柱式和弦結構的四音級合再加上截斷G最后一個雙音的延留，共同組成了一個六音級合并全曲結束，截斷H相當于一個終止和弦的作用。

四、各截斷之間的結構關系

（一）截斷A與截斷C的關系

我們知道截斷A是一個雙音級合，包含G，B兩個集合元素；而截斷C是個四音級合，包含有C，bE，G，B四個集合元素，顯而易見的，截斷A的元素包含于截斷C中，因此它們屬于子集與母集的包含關系，即截斷A是截斷C的具象子集。

（二）截斷D與截斷E的關系

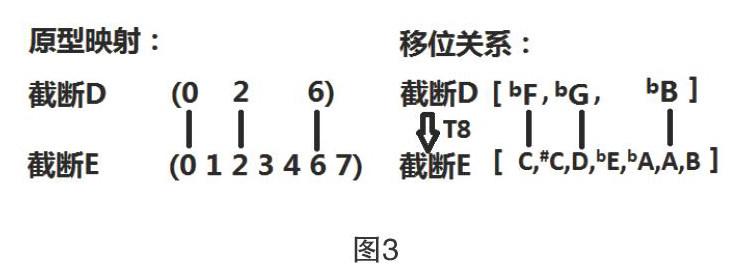
截斷D與截斷E的關系比較隱性，從集合元素上看，截斷D包含bF，bG（#F），bB（#A）三個集合元素，截斷E包含c，#C，D，bE，bA，A，B七個集合元素，從元素上看，兩者似乎無什么關系，但是把兩個截斷進行原型表示后我們會發現截斷D為3-8：（026）；截斷E為7-4：（0123467）。從原型上我們可以看到，截斷D是映射于截斷E的原型的，這表示截斷D其實是截斷E的抽象子集，需要進行移位的操作才會在集合元素上一一映射，移位關系如圖3所示。

（三）截斷B、截斷E與截斷G的關系

同樣作為七音級合的三個截斷，它們之間的關系是值得比較的，而通過觀察后會發現，這三個截斷無論在集合元素上還是在集合原型上都沒有什么聯系，那么它們之間到底什么關系呢？這就需要我們觀察其音程級向量了，觀察音程級向量是為了比較集合間的相似性關系，因此我們需要通過比較音程級向量來確定三者的關系是最大相似性還是最小相似性。比對過后我們呢會發現，截斷B與截斷E、G為最小相似性關系，截斷E與截斷c為最大相似性關系，如圖4所示。

（四）截斷C、截斷F與截斷H的關系

截斷c與截斷F都是四音級合，而截斷H為六音級合，但是仔細觀察截斷H會發現，它是由截斷G最后的雙音和一個四音和弦共同組成的這個六音級合。其組成關系如圖5所示。

因此我們可以在截斷H中得到一個新的四音級合4-19：（0148）。音程級向量為：101310-這個四音級合可以看做截斷H中六音級合的具象子集。這時對比這三個截斷便會發現，這個新的四音級合與截斷C的集合原型相同，二者互為移位關系。而截斷C、截斷H與截斷F互為最小相似性關系，如圖6所示。

五、結語

通過運用集合理論對音樂細節的分析，片段與整體，片段與片段之間的分析等，能夠對整首音樂作品在材料結構上有一個清晰的認識，這也是集合理論作為一種無詞性音樂分析手法所展現的功能與作用。在分析這首作品方面，我們能夠看到各集合截斷所表現的內涵與音樂之間的聯系，包括集合的包含關系、移位關系以及相似性關系等，使得我們能夠總結出這部作品在音樂材料的運用方面，不僅有發展還有對比，音樂語言比較豐富，整個音樂的結構和材料之間的聯系卻十分密切。不可否認這雖然是一首規模小巧的鋼琴小品，但是簡單的集合材料背后卻有著嚴密的邏輯關系，結構不緊不松，精煉新穎。