說說神奇的黃金比例Φ

首先，我們先說說Φ這個符號，它是一個希臘字母，中文發音是“佛愛”或“斐”。這個Φ代表的數字1.618034和第2期講的斐波那契數列有著密切的聯系。怎么密切呢？我們下面對斐波那契數列做一些簡單的運算。

斐波那契數列：1，1，2，3，5，8，13，21，34，55……

將斐波那契數列前后兩個數字相除：

1/1=1， 2/1=2，3/2=1.5，5/3=1.67，8/5=1.6，13/8=1.625，21/13=1.615，34/21=1.619，55/34=1.618……它越來越趨近于1.618034。

數學家和藝術家發現這個奇特的數字已經有幾千年了，很久以來人們認為這個數字具有魔力。萊昂納多·達·芬奇將“Φ”稱作“黃金比例”，并將它應用到繪畫當中，傳說他的名畫《蒙娜麗莎》中的人物面部就非常符合黃金比例。

奇異的Φ

1 ÷Ф=Ф-1 Ф×Ф=Ф+1

Φ具有奇特的屬性。比如說，Φ的平方正好等于Φ加上1。如果你用斐波那契數列中的某個數字除以它前面的一個數字，你將會得到一個近似于Φ的比率。這個比率將隨著數字的增大不斷地趨近于Φ，但是永遠也不會等于Φ。事實上，你無法將Φ用兩個數的比率表示出來，所以數學家將它稱為“無理數”。若你用十進制將Φ寫出來，小數點后的位數將是無窮無盡的。

Φ到底是什么？

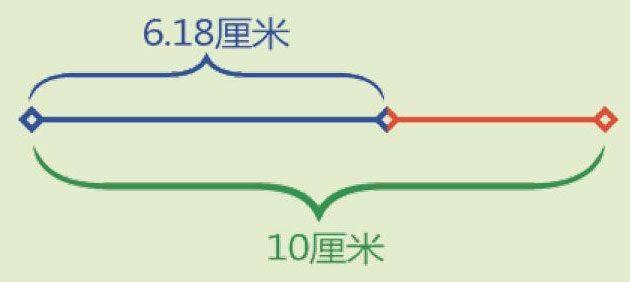
在紙上畫出一條10厘米長的線段，然后在6.18厘米處作上標記。這樣你就將這條線段分成了一長一短的兩部分。若用整條線段的長（10厘米）除以長線段的長（6.18厘米），結果等于1.618。同樣，若用長線段的長（6.18厘米）除以短線段的長（3.82厘米），結果也近似于1.618。這就是“黃金比例”，或者叫做“Φ”。

黃金比例都存在哪里？

古希臘人認為Φ具有魔力，因為它總是出現在那些他們認為很神圣的圖形上。比如說，在正五角星里，長線和短線長度的比率正好是Φ。

黃金螺旋

如果你畫出一個長為Φ寬為1的矩形，你就得到了一個藝術家所說的“黃金矩形”——你所能想到的最美麗的矩形。將這個矩形分割為一個正方形和一個一個小矩形，那么這個小矩形同樣也是一個黃金矩形。只要不斷地將它分割下去，就會出現一個螺旋圖案。這個“黃金螺旋”看上去與一種叫做鸚鵡螺的海洋生物的殼非常相似，但事實上它們是完全不同的。鸚鵡螺殼上的螺旋每旋轉1/2圈，半徑增加為原來的Φ倍，而黃金螺旋則是每1/4圈才會有這樣的變化。

多肉植物

如果你養多肉植物，你會發現有些多肉植物如多葉蘆薈也會呈現出“黃金螺旋”的形狀。植物以“黃金螺旋”的形式生長，能讓新生葉子與舊葉子之間不會相互遮擋太多，能最大程度地享用陽光和雨露。

帕特農神廟

據說古希臘的建筑師們常常把Φ應用到建筑中。很多人都認為雅典帕特農神廟的設計就是基于黃金矩形。你覺得呢？

卡特里娜颶風

2005年襲擊美國的卡特里娜颶風的衛星云圖，你覺得這個風暴是不是一個黃金螺旋？

銀河系

銀河系是一個巨型旋渦星系，呈完美的黃金螺旋狀。