基于“學習循環圈”的數學學習過程設計

摘 要：“自然學習設計”是目前美國當代中小學教育改革的一種重要模式，其核心內容是學習循環圈，借助四個象限呈現，這四個象限關注四類學習風格者. 本文基于“學習循環圈”設計數學學習過程模式，分“為什么——是什么——應怎樣——該是否”四個循環階段. 以對數運算性質為樣例，闡明學習循環圈符合數學知識發生發展的過程，關注學生思維的全面發展.

關鍵詞：學習循環圈；差異施教；對數運算性質

“學習循環圈”理論概述

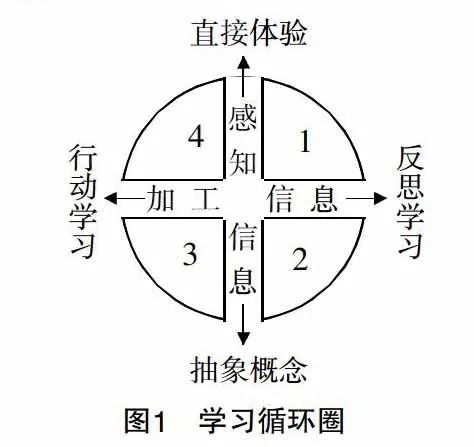
美國教育心理學博士伯尼斯·麥卡錫以提供教學指導為目的，借助四個象限（見圖1）提出了完整的“學習循環圈”. 它就像倒置的冰激凌甜筒，隨著課程的螺旋上升，循環圈上的每一個點所產生的相互關系也會越來越復雜，最佳狀態要等到整個課程螺旋上升結束. 圖1是它的俯視圖，好似一個時鐘，以“感知信息”和“加工信息”為經緯，學習依次經歷了“直接體驗”（12：00）——“反思學習”（3：00）——“抽象概念”（6：00）——“行動學習”（9：00），再融會貫通. 最后帶著新的起點又重新回到“直接體驗”開始新一輪的學習循環圈.

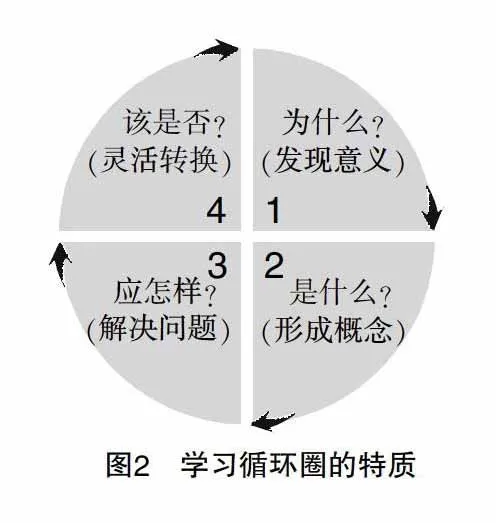
依據學習循環圈開展學習就是學習過程本身，完整的自然學習過程包括“為什么”、“是什么”、“應怎樣”、“該是否”四個象限（見圖2），四個象限關注四類學習風格者. 象限Ⅰ關注想象型學習者：他們傾向于在12：00逗留久一點，最愛問“為什么”，渴望了解知識的內在價值和意義；象限Ⅱ對應分析型學習者：他們傾向于在3：00逗留久一點，最愛問“是什么”，渴望理清知識的內在結構和知識間的聯系，力求掌握概念、理論；象限Ⅲ關注嘗試型學習者：他們傾向于在6：00逗留久一點，最愛問“如何運作”，尋求理論的實用價值，追求做事效率，動手能力強；象限Ⅳ關注創造型學習者：他們傾向于在9：00逗留久一點，最愛問“假如……那該會怎樣”，喜歡從自身的感知和體驗出發，去反思和質疑現有的各種理論，對理論進行補充和修正.要注意，學習循環圈是自變量，四類學習風格者是因變量. 學習循環圈是在符合認知規律的前提下有效地進行差異施教.

基于“學習循環圈”的數學學習過程設計模式

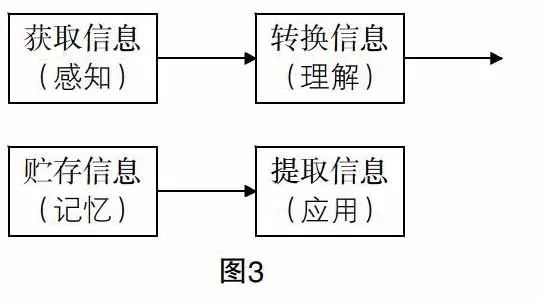
上文提到四類學習風格者，他們喜歡在各自象限逗留久一些，但并不代表他們不需要經歷其他象限. 由加涅的學習與記憶的信息加工模型可知，學習循環圈與學生的認知過程（見圖3）相吻合，而循環圈的獨特性在于既注重學生的認知發展過程，又關注四類學習風格者.

因此每個人的學習都應該經歷這四個階段.

因此在教學中可以依據學習循環圈開展教學，在教師的指導下，開展數學學習，我們將學習過程分為四個階段（見圖1和圖2），如下.

第一階段：“為什么”階段——為意義而教. 從直接體驗（12：00）——反思學習（03：00），發現學習內容的意義和價值.這一階段教師激發學生的想象力，學生建立新舊知識聯系.

第二階段：“是什么”階段——為理解而教. 從反思學習（03：00）——形成概念（06：00），透徹掌握概念. 這一階段教師傳授知識，學生建立專家知識.

第三階段：“應怎樣”階段——為掌握而學. 從形成概念（06：00）——解決問題（09：00）時，積極利用新學內容解決問題. 這一階段教師輔導學生，答疑解惑，學生熟練掌握知識技能，解決問題.

第四階段：“該是否”階段——為創新而學. 從解決問題（09：00）——融會貫通（無限趨近于12：00），加深知識理解，接受新的挑戰. 這一階段教師鼓勵學生積極思維，學生將所學知識融會貫通，靈活應用. 最后學生帶著新的起點又重新回到“直接體驗”開始新一輪的學習循環圈.

基于“學習循環圈”數學學習過程模式既注重數學知識的發生發展過程，又關注學生思維的全面發展和個性差異. 下面以對數運算性質數學學習過程設計為例，闡明學習循環圈為數學教學帶來的啟示和幫助，為學生提供合理的知識學習途徑，為數學教師指出教學實施的有效設計.

基于“學習循環圈”的數學學習過程設計樣例

教材分析：本節選自北師大版普通高中課程標準實驗教科書《數學（必修一）》第三章第四節第二課時. 在前一節學生已經學習了對數概念和對數運算，為本節儲備了知識和技能，由于對數與指數緊密關聯，故對數運算性質學習應類比指數學習步驟. 在本節課中讓學生經歷猜想和推導對數運算性質的過程，養成猜想、歸納和化歸的意識，培養學生提出問題、分析問題、解決問題、創造性思維的能力；讓學生感悟一級運算加減、二級運算乘除、三級運算乘方間的運算關系，感受對數運算的優越性；讓學生深切感受新舊知識間的聯系，學會將復雜的問題簡單化.

教學過程：

1. “為什么”階段

引語：上節課我們一起學習了對數與對數運算，了解了對數在生活中應用廣泛.例如以對數為坐標將天上的星星劃分等級，使用對數求解水溶液的PH值，利用對數算人口增長率、原子的核衰變、地震級數等等. 今天讓我們對對數進行更深入的研究.

（1）引入（使用多媒體PPT）

教師活動1：我們要研究對數，想想對數和哪些知識有關？

學生活動1：回顧舊知（對數源于指數，互化式ab=N?b=logaN（a>0，a≠1且N>0））.

教師活動2：回想我們是如何研究指數的？

學生活動2：思考研究指數的步驟和方法（先是指數概念，再是指數運算性質，最后是指數函數）.

教師活動3：仿照指數，接下來我們應該研究對數的什么內容？如何研究？

學生活動3：學生類比思考答案（指數運算性質對應對數運算性質）.

教師活動4：我們要研究對數的運算，首先清楚基本的數學運算有哪些？

學生活動4：思考基本數學運算有哪些（加、減、乘、除）.

【設計意圖】 就學習過程的本身，只有讓學生意識到知識“為什么”的價值性，學生才會探究知識“是什么”的重要性. 因此“為什么”階段是教師必須完成的過程. 在此階段，教師扮演激發者角色，通過列舉讓學生直接感受所學內容的意義，接著采用類比思想讓學生發現研究對數的方法，緊接著想到如何研究對數運算性質？引發學生認知沖突，拋出課題，完成“為什么”階段. 這一階段關注想象型學習者，使學生明白學習對數的意義和價值，發現指數與對數緊密聯系，明白為什么這樣研究對數.

2. “是什么”階段

（1）猜想

（說明由于對數運算分底數相同和底數不同，本節課解決相較簡單的同底數對數運算）

探究一

教師活動5：請同學們4人小組完成表格.第一組數據：M=8，N=32，計算log2M+log2N，log2M-log2N，log2M·log2N，，log2（M+N），log2（M-N），log2（M·N），log2. 第二組數據：M=3.141596，N=2.718281，計算lgM+lgN，lgM-lgN，lgM·lgN，，lg（M+N），lg（M-N），lg（MN），lg. 通過計算猜想對數運算性質（計算器輔助）.

學生活動5：小組計算，討論，得出猜想.

（1）logaM+logaN=loga（M·N）.

（2）logaM-logaN=log（a>0且a≠1，M>0，N>0）.

【設計意圖】 依據“是什么”階段，這是循環圈的傳授環節，教師扮演傳授者的角色幫助學生建立與專家知識間的聯系. 對于本節課而言，設置猜想環節，根據最基本的加減乘除和指數運算性質，探索對數運算性質. 讓學生經歷猜想、歸納、化歸的過程. 這一階段關注分析型學習者，幫助他們學會分析問題，為發現理論和公式打下基礎.

（2）證明

探究二

教師活動6：如何證明對數運算性質logaM+logaN=loga（M·N）？

學生活動6：思考證明對數的方法.

【設計意圖】 學生正在經歷“是什么”階段，在探索二中，學生對于對數源于指數十分熟悉，證明方法多樣. 設置預設補充環節，幫助學生理解化歸這一數學思想方法. 通過探究三和探究四，學生可以發現知識間緊密聯系，從而加深他們對知識的理解，深入認識劃歸思想. 提高推理歸納能力、分析問題的能力，完成“是什么”階段. 這一階段關注分析型學習者，幫助他們完善知識結構，理清知識脈絡.

3. “應怎樣”階段

教師活動12：講解例題，輔導練習.

學生活動12：進行“左推右”，“右推左”兩種方式的運算，掌握解題方法和技巧.

【設計意圖】 依據“應怎樣”階段，利用何小亞教授設計的對數運算測試量表優化例題，設置有梯度的題目. 設計例1、例2和例3可以加深學生對對數運算性質的理解和掌握. 有利于學生建立“A=B”時，“左推右”——將一級運算化為二級運算，實現了式子的簡化；“右推左”——將二級運算或三級運算化為一級運算，實現了將“大數”化為“小數”，這兩種運算途徑. 最后完成“應怎樣”階段.這一階段關注常識型學習者，教師幫助他們發現對數運算規律和技巧，培養學生的解決問題的能力.

4. “該是否”階段

教師活動13：請同學們談談這節課的收獲.

學生活動13：回想本節課所學知識內容和思想方法.

思考1：還有沒有其他證明對數運算性質的方法（提示：使用alogaN=N，logaab=b）.

思考2：如果底數不同又該如何計算？為什么計算器上只有以10為底的對數？

【設計意圖】 學生活動13旨在讓學生對本節課的內容融會貫通. 思考1是依據“該是否”階段，為創造而學，提示學生證明對數運算性質還有其他方法，激發學生的興趣和求知欲. 思考2則是為下節課的開展打好基礎，讓學生做好預習. 通過課后學習完成“該是否”階段. 這一階段關注創造型學習者，為他們獲得更多的證明方法和增生新的問題提供指導和方向.

基于“學習循環圈”進行數學學習過程設計的優勢

對數學教學而言，要特別關注兩個過程：一是數學知識的發生發展過程；二是學生的思維過程. 依據“學習循環圈”設計的數學學習過程模式正是從數學知識發生發展過程的角度構建的學習過程，并且設計的數學學習過程與學生認知過程相融合，進而有效培養學生思維能力.

1. 符合數學知識發生發展過程

一般來說，數學研究的問題可以歸納為兩類：一類是研究對象與對象之間的關系，另一類是研究對象要素之間的關系. 對數學教學而言就是引導學生探索對象之間或對象要素之間的關系，并在此過程中暴露知識的發生發展過程. 本文依據“學習循環圈”設計的樣例《對數運算性質》正是在研究指數與對數兩個對象間的關系，以及對數的和、差、乘方要素間的關系，因此“學習循環圈”能有效幫助學生經歷知識發生發展過程，培養學生發現研究對象的能力、圍繞研究對象確定研究角度的能力以及尋找知識之間聯系規律的能力.

2. 注重學生思維全面發展

首先，符合學生的認知規律. 依據加涅的學習與記憶的信息加工模型，我們可以知道基于“學習循環圈”數學學習過程設計把學生的認知規律和數學知識發生發展的過程相融合，如類比指數學習方式研究對數，再如通過公式（1）推導出減法公式和乘方公式，強調問題的預設和生成. 其次，培養學生的“四能”.數學學習過程的四個階段依次培養學生提出問題的能力、分析問題的能力、解決問題的能力、創新性思維能力，這一學習過程有效促進學生思維的全面發展. 最后，注重因材施教. 在學習過程設計模式的不同階段中，教師關注不同的學習風格者. 總之，就是“投其所好”，差異施教，促進四類學習者的個性發展.