基于經典微擾理論的特征值靈敏度和不確定度分析

劉 勇，曹良志，吳宏春，祖鐵軍

(西安交通大學 核科學與技術學院，陜西 西安 710049)

?

基于經典微擾理論的特征值靈敏度和不確定度分析

劉 勇，曹良志，吳宏春，祖鐵軍*

(西安交通大學 核科學與技術學院，陜西 西安 710049)

核數據不確定度作為組件/柵元計算不確定度的重要來源，備受重視和研究。本文采用經典微擾理論，推導輸運計算中keff對于核數據的靈敏度系數和不確定度的計算方法。基于ENDF/B-Ⅶ.1制作多群協方差數據庫，并根據所采用的組件輸運求解程序的截面模型對分反應道協方差矩陣進行歸并。開發靈敏度和不確定度分析程序COLEUS，對傳統壓水堆燃料柵元進行計算分析。數值結果表明，柵元計算的keff對235U每次裂變中子產額的擾動最為敏感，238U俘獲截面對keff不確定度的貢獻最大。目前的核數據的不確定度會給keff帶來0.4%～0.5%的不確定度。

微擾理論；協方差；靈敏度；不確定度

在核反應堆計算中，由于在計算模型、輸入參數和經驗修正等方面的不足，使得計算結果存在一定的不確定度。對重要參數靈敏度和不確定度的量化，不僅有利于確定合理的設計裕量，提高核反應堆設計的經濟性，還可指導核數據評價的優化方向。

核反應堆的計算從最初的柵元(組件)計算到堆芯計算，再到最終的核反應堆系統計算的各個階段，都存在不確定度的引入和傳遞[1]。作為核反應堆計算的基礎，柵元(組件)計算的不確定度來源有如下3方面[2]：1) 模型、計算方法和近似引入的偏差；2) 反應堆系統的物理參數測量偏差，如密度、尺寸等；3) 基本物理參數的偏差，如截面數據等。而第3個方面中的中子反應截面被認為是該計算過程最重要的不確定度來源之一[3]。

目前國際上以UAM(uncertainty analysis in modelling)[1]等為代表的合作項目，正在廣泛地開展針對反應堆計算敏感性和不確定性的分析。核數據的分析作為敏感性和不確定性分析中重要的一個環節，備受重視，其中的代表程序有TSUNAMI[4]、ERANOS[5]、SUSD3D[6]等。這些程序主要關注核數據的擾動和其測量不確定度導致的積分參數(keff、反應率、冷卻劑空泡反應性系數等)的擾動和不確定度。近年來國內也在這方面展開研究工作，具有代表性的程序有SUCA1D[7]、SURE[8]等，但這些程序均限于一維計算，研究的積分參數類型也較為局限。因此，本文關注核數據對計算結果的影響，包括keff對核數據擾動的靈敏度以及在當前核數據的測量精度下keff的不確定度。基于經典微擾理論，采用子群共振方法程序SUGAR[9]和二維任意幾何特征線輸運程序AutoMOC[10]，開發靈敏度和不確定度分析程序COLEUS，并對柵元計算中keff對中子反應截面的靈敏度和中子反應截面的不確定度對keff造成的不確定度進行計算和分析。

1 理論方法

1.1 靈敏度系數計算方法

在反應堆物理柵元計算中，典型過程包括共振計算和輸運計算。如果只考慮參數α的擾動在輸運方程中的作用，這種直接影響稱為顯式敏感性；如果考慮參數α在共振計算過程中對共振截面的作用，繼而間接影響到輸運方程的求解，這種間接影響稱為隱式敏感性[11]。本文主要關注顯式靈敏度系數及其不確定度的計算，在確定論方法中，顯式靈敏度系數的計算常采用微擾理論[12]。

中子輸運方程的算子形式為：

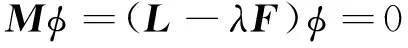
(1)

其中：φ=φ(r，Ω，E)為中子角通量密度；λ為方程的特征值，λ=1/keff；M為輸運算子；F為裂變源項算子；L為輸運算子中除裂變源項算子以外的其他算子。

中子輸運方程的共軛方程為：

(2)

其中：φ*=φ*(r，Ω，E)為共軛中子角通量密度；M*為輸運算子的共軛算子；F*為裂變源項算子的共軛算子；L*為輸運算子中除裂變源項算子以外的其他算子的共軛算子。

給系統一個微小的擾動后，算子M變成M′=M+δM，或記作：

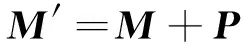
(3)

P=δM稱為擾動算子。設擾動后的中子通量密度φ′滿足：

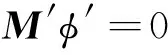
(4)

或

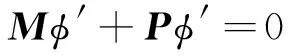
(5)

將擾動前的中子共軛通量密度φ*同式(5)兩端作內積，得到：

(6)

其中，〈·，·〉表示在相空間作內積。由于M*和M共軛，并假定邊界條件未受到擾動，則有：

(7)

而M*φ*=0，于是得到：

(8)

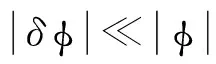
(9)

式(9)稱為擾動方程。

由于M=L-λF，則：

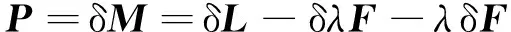
(10)

將式(10)代入式(9)，得：

(11)

從而有：

(12)

由于λ=1/keff，所以：

(13)

根據靈敏度系數的定義[1]，有：

(14)

從式(14)可看出，式中算符對核數據的偏導項容易求得，所以只需一次前向輸運計算和一次共軛輸運計算得到前向中子角通量密度和共軛中子角通量密度，就能得到keff對包含在輸運算子中的所有參數的靈敏度系數。本文采用子群共振方法程序SUGAR進行共振計算，采用二維任意幾何特征線輸運程序AutoMOC進行前向輸運計算，以獲得中子角通量密度；并對該輸運程序進行改進，獲得中子共軛角通量密度，然后根據式(14)計算keff對核素各種截面的靈敏度系數。

1.2 不確定度計算方法

keff可認為是截面的函數，寫成如下函數形式：

(15)

將keff在σi的期望值σi0處進行泰勒一階展開：

(16)

設σi的方差為V(σi)，keff的方差為V(keff)，對式(16)等號兩邊取方差得到：

(17)

其中，cov(σi，σj)為σi和σj的協方差，用來衡量兩個變量的總體誤差。式(17)即為不確定度傳播率，該式將截面數據的不確定度傳遞給keff。

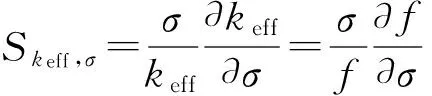
(18)

(19)

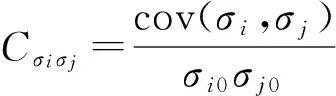
1.3 協方差數據

早期核數據的評價庫往往只給出核數據的一階矩，即期望值。從ENDF/B-Ⅳ開始，評價庫中就包含了一些核素的核數據的概率分布的二階矩，即協方差[14]，包括每次裂變的中子產額、共振參數、中子截面、次級粒子能量和角度分布、放射性核素產額等數據的協方差信息[1]。協方差數據文件提供了核數據的相關性和不確定度。從式(19)可看出，只要得到核數據的相對協方差信息，就能結合靈敏度系數，通過Sandwich Rule公式，計算積分參數(如keff)的不確定度。

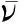
NJOY制作的多群協方差數據是各種分反應道的協方差數據，而大多基于確定論的中子輸運計算程序使用的截面模型是將各分反應道截面以求和形式給出的散射、俘獲截面，因此需要散射、俘獲截面的協方差，這樣的協方差數據無法從NJOY直接得到。一般有3種方法處理這種問題[3]：1) 修改程序的截面模型；2) 使用同問題無關的截面數據來計算keff對各反應道截面的靈敏度系數；3) 制作與輸運程序截面模型一致的協方差數據庫。本文采用第3種方法，將制作的分反應道協方差信息轉換成這種求和形式的截面的協方差信息。本文采用的截面模型中，俘獲截面為：

(20)

其中，NG為能群總數。

由于俘獲截面和散射截面同其分反應道截面是線性關系，所以由向量的協方差計算關系式可知：

(21)

其中：Kc為NG×8NG的系數矩陣；cov(σKc)為各反應道之間8NG×8NG的協方差矩陣。

本文采用的散射截面模型的形式為：

g=1，NG

(22)

同樣可知：

(23)

其中：Ks為NG×4NG的系數矩陣；cov(σKs)為各反應道之間4NG×4NG的協方差矩陣。

基于ENDF/B-Ⅶ.1制作的172群協方差數據庫中，俘獲反應的分反應道中存在協方差數據的中子核反應包括(n，2n)、(n，3n)和(n，γ)反應。評價庫中無其他分反應道協方差信息，假設為零。圖1為基于ENDF/B-Ⅶ.1制作的238U的172群俘獲反應各分反應道的相對協方差與歸并得到的俘獲截面的相對協方差矩陣。

由于(n，2n)和(n，3n)反應為閾能反應，所以圖2只示出了前10能群的俘獲截面及其分反應道截面隨能群的變化曲線。

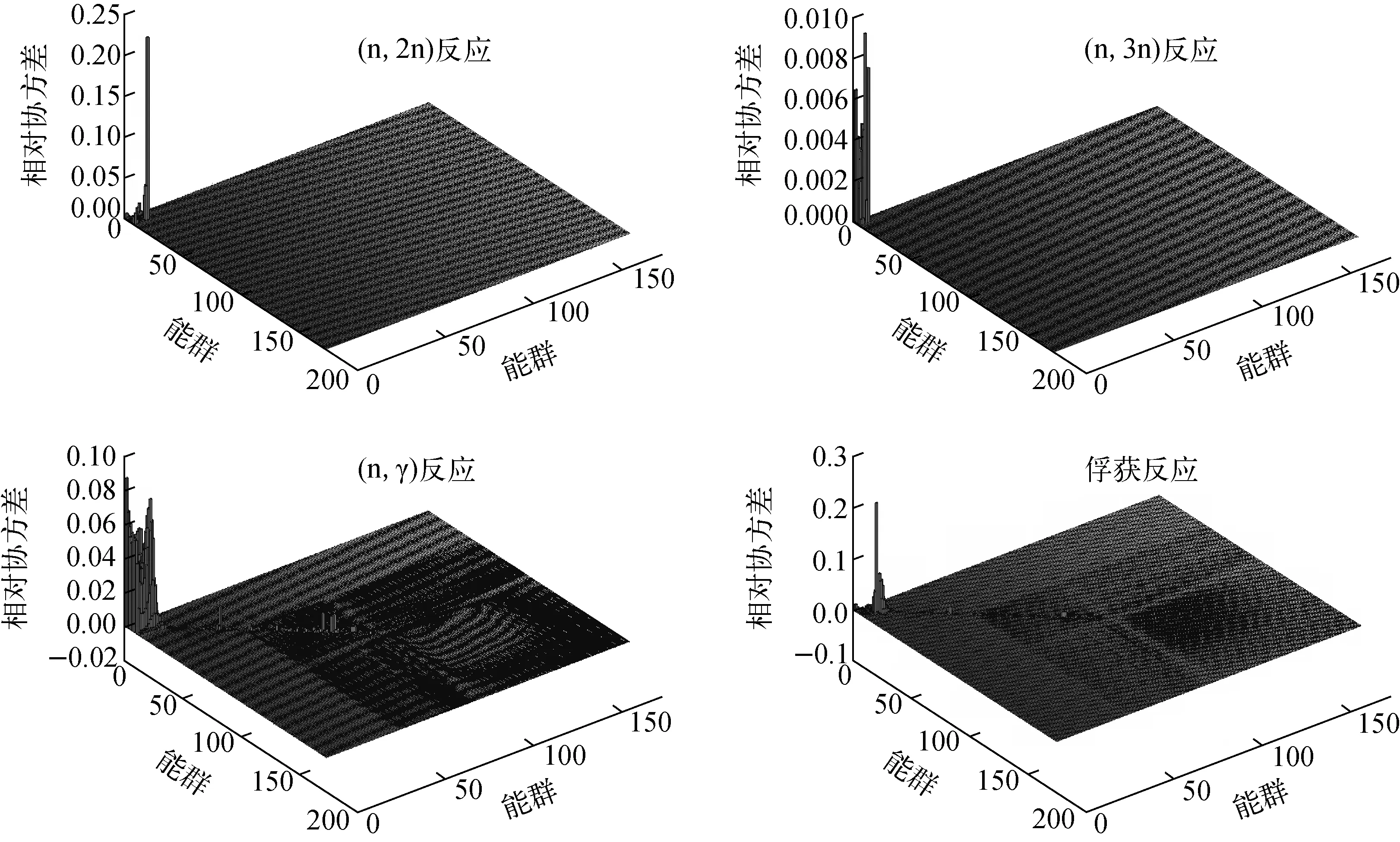
圖1 238U俘獲截面及其分反應道截面的相對協方差矩陣Fig.1 Relative covariance matrices corresponding to total capture cross section and individual capture cross section of 238U

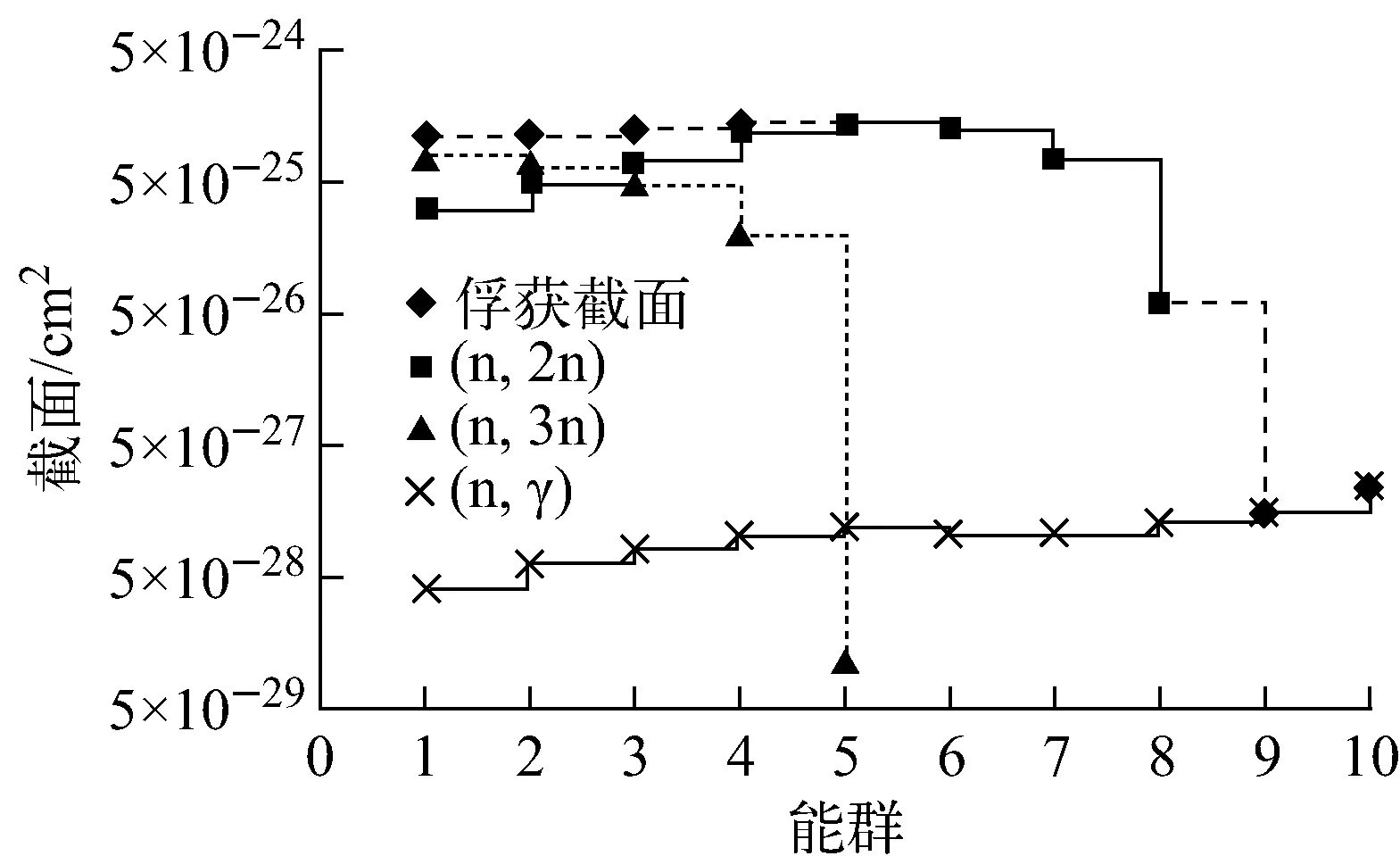
圖2 238U前10能群俘獲截面及其分反應道截面Fig.2 Total capture cross section and individual capture cross section of first ten energy groups of 238U

從圖1、2可發現，雖然238U(n，γ)反應的相對協方差在高能群較大，但由于其截面值小，所以在歸并成俘獲截面相對協方差后，(n，γ)反應高能群相對協方差對俘獲截面相對協方差的貢獻并不大。俘獲截面高能群的相對協方差主要來自(n，2n)和(n，3n)反應。值得注意的是，核數據的協方差大小并不能最終決定其對結果的不確定度貢獻，這需要結合靈敏度進行計算。

基于上述理論分析，本文敏感性和不確定性分析的計算流程圖如圖3所示。

圖3 敏感性和不確定性計算流程圖Fig.3 Flow chart of sensitivity and uncertainty calculation

2 計算結果

利用本文開發的程序COLEUS，對典型輕水堆燃料柵元進行靈敏度和不確定度分析，該問題來自OECD UAM LWR基準題[1]：TMI-1壓水堆燃料組件柵元。

表1列出了該問題前向和共軛keff的計算結果，以及截面數據導致的keff相對不確定度的計算結果，本文用Δkeff(標準偏差)表示keff的不確定度，Δkeff/keff表示keff的相對不確定度。其中TSUNAMI-1D和CASMO-4的結果均來自文獻[3]，二者輸運計算采用的截面數據庫基于ENDF/B-Ⅵ，本文采用的數據庫基于ENDF/B-Ⅶ.0制作。本文計算得到的keff的總不確定度為0.416 7%，較參考結果偏小。其原因是本文采用的核數據相對協方差與參考結果采用的相對協方差數據有部分不一致，此外能群結構對于靈敏度系數和協方差矩陣的制作也存在影響，同樣會導致不確定度計算結果的差異。但可發現，當前核數據的精度在傳統壓水堆柵元計算中對keff造成的不確定度在0.5%左右。

表1 keff及其不確定度計算結果Table 1 Calculation results of keff and its uncertainty

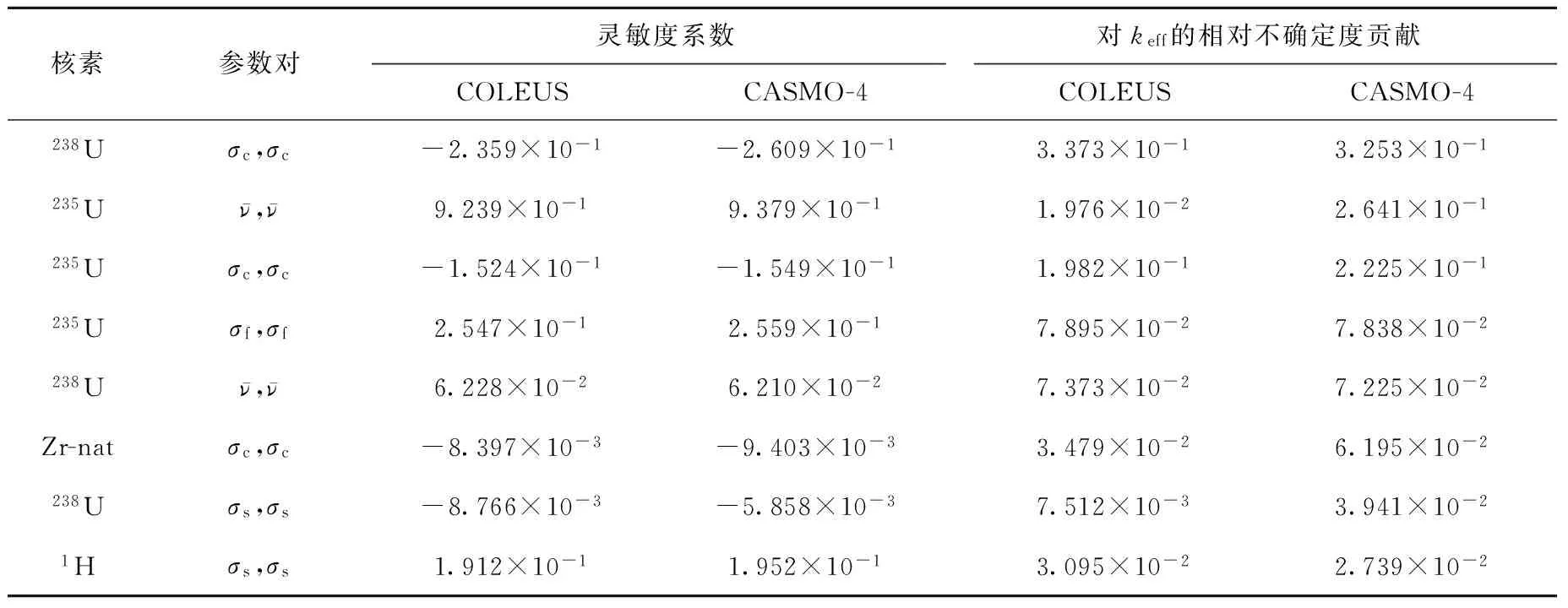
表2 PWR柵元中重要的不確定度來源及相對靈敏度系數Table 2 Most important sources of uncertainty in PWR pin-cell case and relative sensitivity coefficients

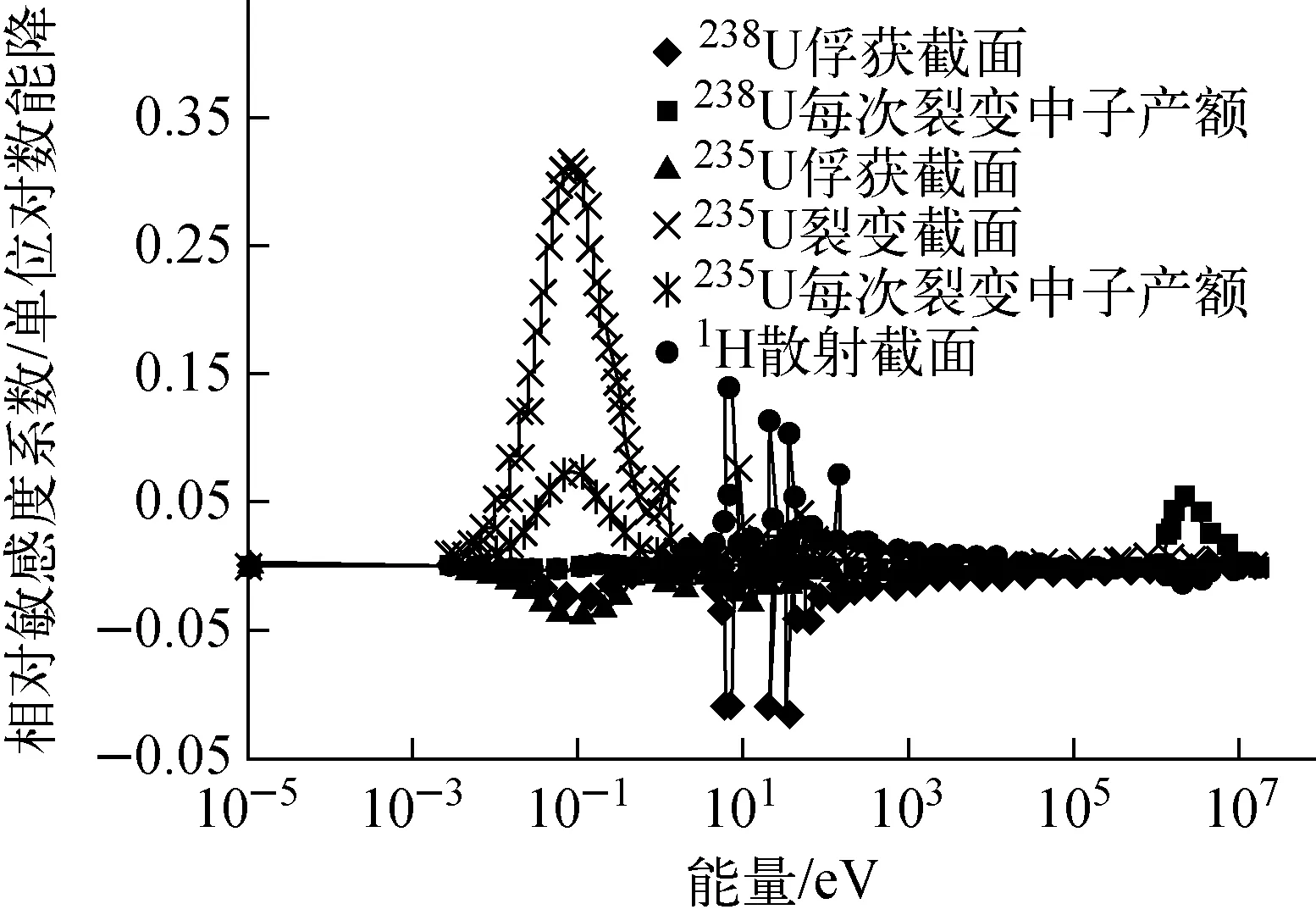
圖4 重要反應的靈敏度系數Fig.4 Sensitivity coefficients of some important reactions

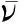
3 小結

微擾理論是計算微小擾動對響應影響的有效方法。基于經典微擾理論，開發了靈敏度和不確定度計算程序COLEUS，采用該程序分析了柵元計算中keff對各核素截面數據的靈敏度系數以及各核素截面對keff不確定度的貢獻。

計算結果表明，截面不確定度對keff不確定度的貢獻取決于靈敏度系數和協方差數據，keff對235U的每次裂變中子產額的擾動最為敏感，而238U俘獲截面對keff的不確定度的貢獻最大。目前核數據的測量精度會給傳統壓水堆UO2燃料柵元計算keff帶來0.4%～0.5%的不確定度。

[1] IVANOV K, AVRAMOVA M, KAMEROW S, et al. Benchmarks for uncertainty analysis in modelling (UAM) for the design, operation and safety analysis of LWRs, Vol Ⅰ: Specification and support data for neutronics cases (Phase Ⅰ), Version 2.1 (final specifications)[R]. [S. l.]: OECD Nuclear Energy Agency, 2013.

[2] WEISBIN C R, MARABLE J H, LUCIUS J L, et al. Application of FORSS sensitivity and uncertainty methodology to fast reactor benchmark analysis[R]. Oak Ridge: Oak Ridge National Laboratory, 1976.

[3] PUSA M. Incorporating sensitivity and uncertainty analysis to a lattice physics code with application to CASMO-4[J]. Annals of Nuclear Energy, 2012, 40(1): 153-162.

[4] REARDEN B T, HOPPER C M, ELAM K R, et al. Applications of the TSUNAMI sensitivity and uncertainty analysis methodology[C]∥ICNC2003. Tokai, Ibaraki, Japan: Japan Atomic Energy Research Institute, 2003.

[5] TAMAGNO P, Van ROOIJEN W F G, TAKEDA T, et al. Sensitivity analysis of Monju using ERANOS with JENDL-4.0[C]∥PHYSOR 2012. Knoxville, Tennessee, USA: American Nuclear Society, 2012.

[6] KODELI I. Multidimensional deterministic nuclear data sensitivity and uncertainty code system: Method and application[J]. Nuclear Science and Engineering, 2001, 138(1): 45-66.

[7] 剛直，周培德. 由截面不確定度引起積分參數keff不確定度一維分析程序開發[C]∥第十二屆反應堆數值計算與粒子輸運學術會議. 合肥：中國核學會，2008.

[8] 胡澤華，王佳，孫偉力，等. 基準模型keff對核數據的靈敏度分析及不確定度量化[J]. 原子能科學技術，2013，47(增刊)：312-317.

HU Zehua, WANG Jia, SUN Weili, et al. Sensitivity and uncertainty analysis of calculatedkeffon benchmark models due to uncertainties of nuclear data[J]. Atomic Energy Science and Technology, 2013, 47(Suppl.): 312-317(in Chinese).

[9] 劉慶杰. 二維任意幾何子群共振計算方法研究及其應用分析[D]. 西安：西安交通大學，2010.

[10]陳其昌. 任意幾何特征線方法及其在直接循環堆組件計算中的應用研究[D]. 西安：西安交通大學，2010.

[11]WILLIAMS M L, BROADHEAD B L, PARKS C V. Eigenvalue sensitivity theory for resonance-shielded cross sections[J]. Nuclear Science and Engineering, 2001, 138(2): 177-191.

[12]謝仲生，鄧力. 中子輸運理論數值計算方法[M]. 西安：西北工業大學出版社，2005.

[13]BALL M R. Uncertainty analysis in lattice reactor physics calculations[D]. McMaster: McMaster University, 2012.

[14]MacFARLANE R E, MUIR D W, BOICOURT R M, et al. The NJOY nuclear data processing system, Version 2012[R]. USA: Los Alamos National Laboratory, 2012.

[15]WILLIAMS M L, WIARDA D, ARBANAS D, et al. SCALE nuclear data covariance library[R]. Oak Ridge: Oak Ridge National Laboratory, 2009.

[16]MERCATALI L, IVANOV K, SANCHEZ V H. SCALE modeling of selected neutronics test problems within the OECD UAM LWR’s benchmark[J]. Science and Technology of Nuclear Installations, 2013, 2013: 1-11.

[17]KAMEROW S, IVANOV K, MORENO C A. Uncertainty analysis of light water reactor unit fuel pin cells[C]∥2011 International Conference on Mathematics and Computational Methods Applied to Nuclear Science and Engineering. Rio de Janeiro, RJ, Brazil: American Nuclear Society, 2011.

Eigenvalue Sensitivity and Uncertainty Analysis Based on Classical Perturbation Theory

LIU Yong, CAO Liang-zhi, WU Hong-chun, ZU Tie-jun*

(SchoolofNuclearScienceandTechnology,Xi’anJiaotongUniversity,Xi’an710049,China)

The uncertainty of nuclear data is being paid to more and more attention because it is one of the most important uncertainty sources in lattice calculation. The expressions of sensitivity and uncertainty ofkeffwith respect to the cross sections were deduced based on the classical perturbation theory. A covariance library was made based on ENDF/B-Ⅶ.1, and the individual covariance matrices of cross section were combined according to the cross section model for lattice calculation in this work. A code COLEUS (calculation tool for evaluating uncertainty and sensitivity) was developed for the sensitivity and uncertainty analysis, and a traditional PWR fuel pin cell problem was calculated and analyzed. Numerical results indicate thatkeffof lattice calculation is the most sensitive to the perturbation of the average number of neutrons released per fission of235U, while the capture cross section of238U has the biggest contribution to the final uncertainty. The measuring accuracy of present nuclear data will bring an uncertainty about 0.4%-0.5% forkeff.

perturbation theory; covariance; sensitivity; uncertainty

2014-03-25;

2014-07-15

國家自然科學基金資助項目(91226106)

劉 勇(1988—)，男，四川成都人，博士研究生，核能科學與工程專業

*通信作者：祖鐵軍，E-mail: tiejun@mail.xjtu.edu.cn

TL32

A

1000-6931(2015)07-1247-07

10.7538/yzk.2015.49.07.1247