利用HRRP序列提取彈道目標進動周期

何興宇，童寧寧，胡曉偉，陳振宇

(1.空軍工程大學 防空反導學院，陜西 西安 710051； 2. 中國人民解放軍95784部隊，四川 成都 614100)

利用HRRP序列提取彈道目標進動周期

何興宇1，童寧寧1，胡曉偉1，陳振宇2

(1.空軍工程大學 防空反導學院，陜西 西安 710051； 2. 中國人民解放軍95784部隊，四川 成都 614100)

進動是中段彈頭的特有屬性，依靠提取進動周期進行目標識別有很大的理論和實際意義。首先建立了中段彈頭的圓環邊緣滑動散射點模型，并給出各散射點的坐標表示。在此基礎上，利用解線頻調算法，通過控制慢時間采樣間隔獲取一維距離像序列，得到目標在不同姿態角下的成像結果。最后，分析成像序列特征，提出了一種新的進動周期估計算法。仿真實驗表明，所提方法能夠準確有效地提取目標的進動周期。

進動；散射點；成像序列；周期；估計

0 引言

彈頭在中段要進行姿態控制，其中自旋是最常用的姿態控制方式，同時由于大氣擾動、誘餌釋放等橫向干擾的作用，自旋錐體目標會產生進動[1-4]。依靠提取彈頭目標固有的進動特征進行彈道目標識別是當前研究的熱點之一。利用HRRP (high resolution range profile，一維距離像)和二維ISAR(inverse synthetic aperture radar，逆合成孔徑雷達)像提取目標特征信息是進行彈道目標識別的重要方法。一維距離像能攜帶的信息少并且敏感于目標的姿態變化，而ISAR像可以通過橫向分辨將這些距離上重合的點分開，提高目標的信息量[5]，但是獲取目標的二維像需要較長的相干積累時間。文獻[6]基于雷達散射截面積(radar cross section，RCS)時間序列估計進動參數，但目標RCS受進動影響較大，在進動參數估計完成之前，其RCS序列估計誤差較大。文獻[7]提出通過分析經驗模式分解(empirical mode decomposition, EMD)結果獲得目標的自旋頻率、錐旋頻率等特征信息，但是計算量和存儲量大，并且如果EMD分解方向確定不準確，容易對后續處理造成較大的誤差。

本文針對一維距離像和二維ISAR像提取目標特征的不足，在不考慮散射中心遮擋的情況下，提出在無翼錐體目標滑動散射點模型下，利用一維距離像序列提取目標的進動周期。進而帶來目標一維距離像的周期性變化，通過一維距離像的周期性來反演目標進動周期。仿真實驗表明，該方法簡單有效，并且在信噪比較低時仍能較準確地提取目標進動周期。

1 滑動散射點進動模型

1.1 進動模型建立

彈頭的進動是自旋和錐旋的疊加，當彈頭為旋轉對稱體時，自旋運動并不影響電磁波的散射特性，因而認為，自旋不會對目標的一維距離像產生影響[8-10]。

已有文獻對進動的建模大都基于理想散射點模型。文獻[11]中指出中段彈道目標在圓錐底部、錐柱結合部等部位的散射中心位置變化與目標本身的微動規律并不一致，屬于圓環結構邊緣滑動散射中心，是典型的非理想散射中心。所以，需要重新構建彈道目標進動模型，該模型應比較正確地反映彈道目標的微動和散射特征。本文構造參考坐標系下的平底錐彈道目標進動模型如圖1所示。

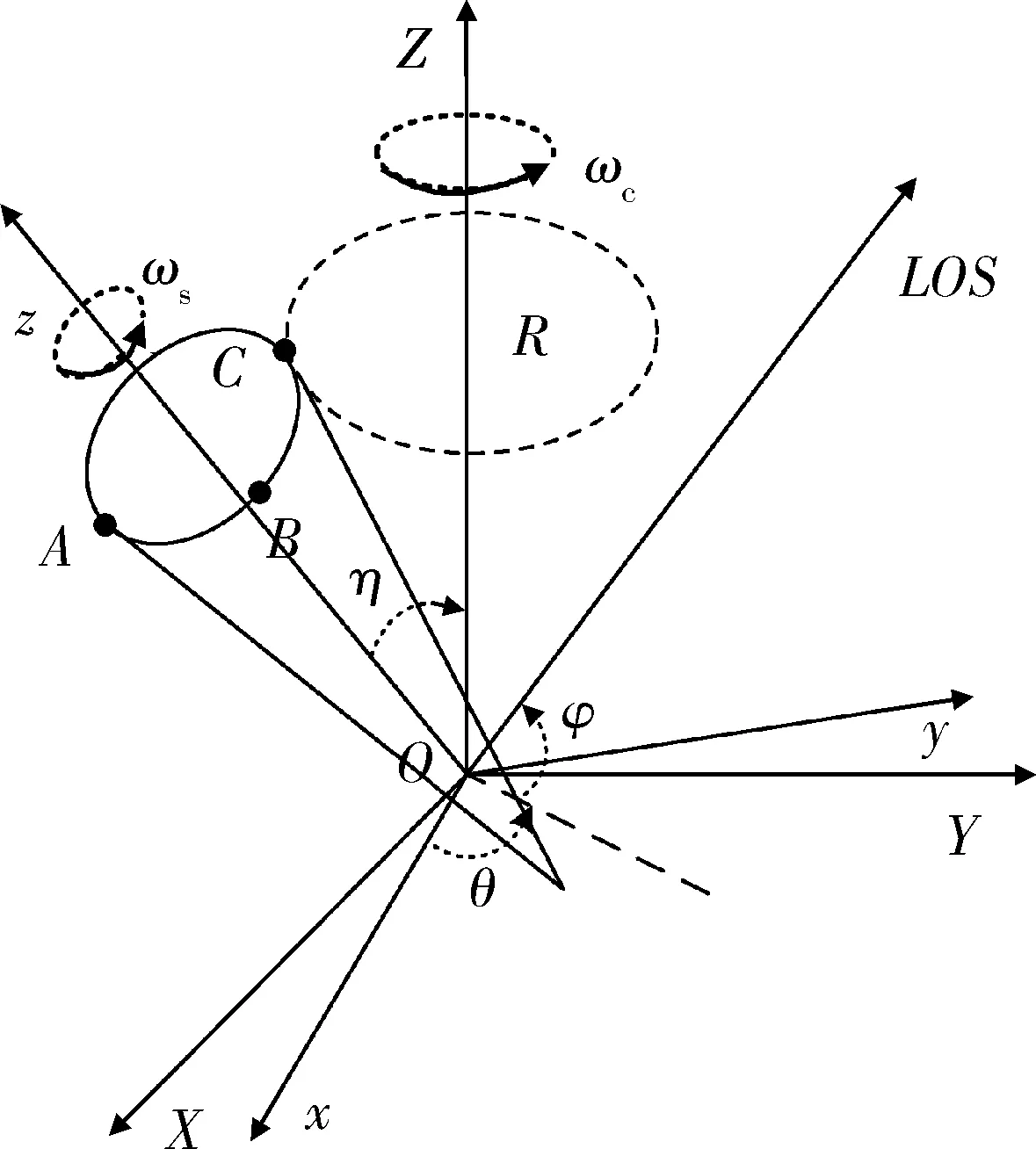
圖1 參考坐標系中目標位置Fig.1 Target’s position in reference coordinate system

以目標旋轉中心為坐標原點O，以目標錐旋軸為Z軸，Y軸位于初始時刻彈體對稱軸與錐旋軸構成的平面內，與錐旋軸OZ垂直，OX,OY與OZ構成右手坐標系。η為彈體對稱軸與錐旋軸的夾角，稱為進動角，θ和φ分別表示雷達視線在參考坐標系中的方位角和俯仰角。 (x,y,z)為本體坐標系，彈體對稱軸為Oz軸，Ox軸位于OZ與Oz構成的平面內，Ox與Oz垂直，Ox，Oy與Oz構成右手坐標系。

1.2 滑動散射點坐標表示

這里主要考察模型的滑動散射點，若同時考慮運動規律簡單的錐頂理想散射中心，其步驟與下面類似。

散射點A，B，C在本體坐標系中的坐標可分別表示為

(1)

式中：r為錐底半徑；z0為各點在本體坐標系中z軸的坐標位置，它在目標進動過程中為常數，在下面的分析中取z0為1。

由Euler旋轉矩陣得到本體坐標系到參考坐標系的變換矩陣為

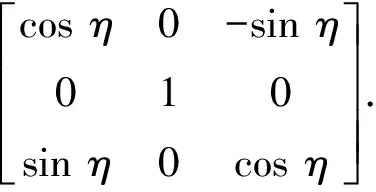
(2)

式中：φ0為初始時刻Oz在OXY平面上的投影與OX的夾角。

t時刻散射點在參考坐標系的位置為

rp(t)=Rconv(x,y,z)T.

(3)

雷達視線在參考坐標系中的單位向量n可表示為

n=(cosθcosφ,sinθcosφ,sinφ)T,

(4)

可得散射點在雷達視線上的距離為

R=R0+rp(t)n,

(5)

式中：R0為原點O在雷達視線上的距離。通過式(5)可求得散射點A，B，C在雷達視線上的距離。

2 基于解線頻調的成像序列

假設雷達發射線性調頻信號為[12]

(6)

在雷達視線上距離為R的散射點的差頻輸出為

(7)

式中：RΔ=Ri-Rref，Rref為參考距離。

將式(7)的差頻信號進行快時間FFT，由此得到在差頻域的表示式：

Sif(fi,tm)=

(8)

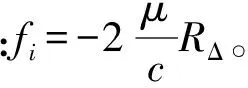
通常進行目標成像，雷達需要發射時寬帶寬積較大的信號，脈沖寬度通常在幾百μs左右，而彈道目標的進動周期一般不超過5 Hz。在脈沖重復頻率為幾百甚至上千Hz情況下，在相鄰慢時間里目標進動帶來的姿態變化很小，其成像結果并沒有太大變化，所以并不需要獲取太密集的成像序列。但是慢時間間隔的選取會影響周期估計的精度，間隔越小，提取的進動周期誤差越小。

3 進動周期估計

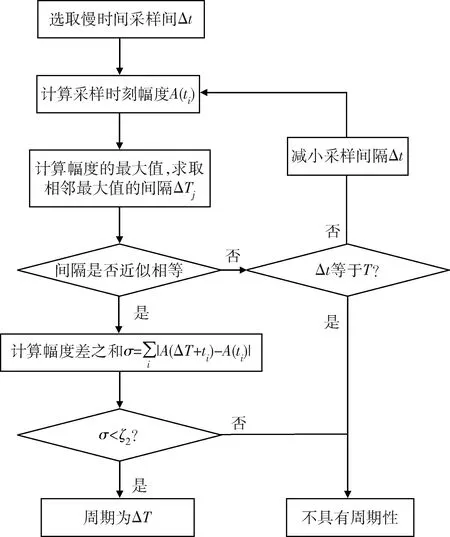
圖2 進動周期估計流程圖Fig.2 Flow chart of precession period estimation

慢時間采樣間隔的選取影響進動周期提取性能，如果選取的采樣間隔能被進動周期整除，則提取效果最好，否則需要減小采樣間隔以減小進動周期估計誤差。

4 仿真分析

4.1 仿真參數設置

目標進動模型仿真參數設置如下：初始相位角φ0=π/2，錐旋頻率fc=1 Hz，雷達視線在參考坐標系中的方位角θ=30°，俯仰角φ=45°，進動角η=15°，錐底半徑為0.5 m，發射信號中心頻率fc=5 GHz，信號帶寬B=1 GHz，采樣頻率Fs=2B，脈沖重復頻率prf=1 kHz，脈沖寬度Tp=100 μs，調頻斜率μ=B/Tp。

在上述的仿真參數設置下，取慢時間采樣間隔為0.1 s，在0～3 s的時間里，有31個慢時間采樣時刻。

4.2 不同信噪比下的仿真結果

當信噪比為5 dB時，得到目標的成像序列結果如圖3所示，圖4為圖3的投影圖，從投影圖中能更準確地判斷其周期性。

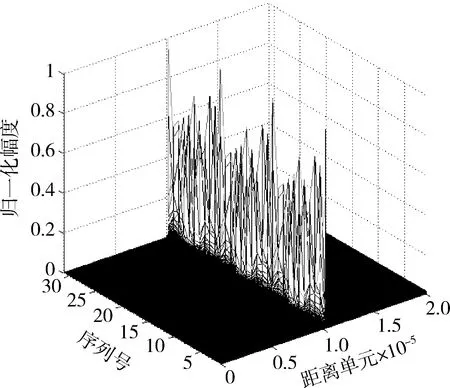
圖3 成像序列圖Fig.3 HRRP sequence

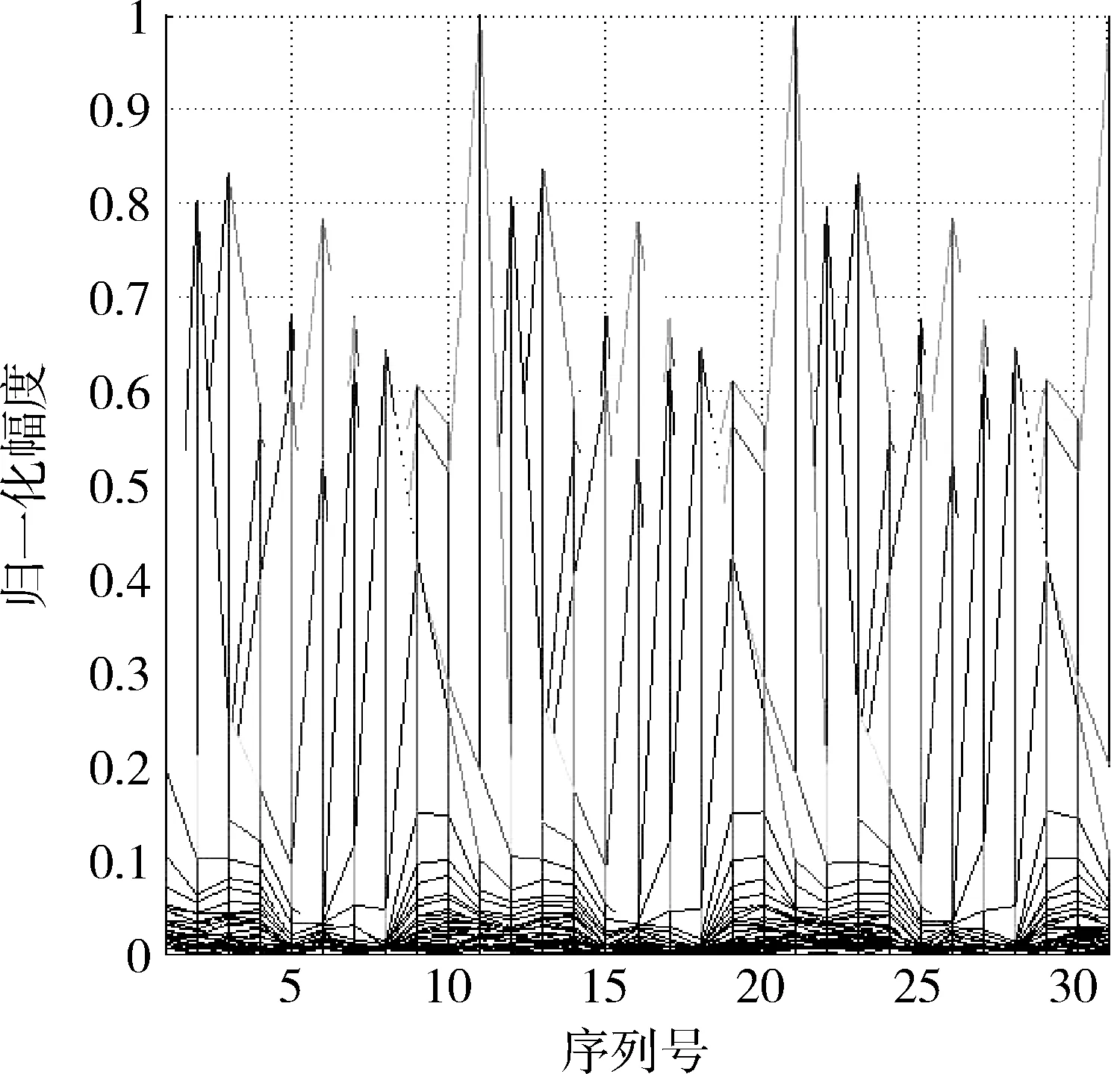
圖4 成像序列投影圖Fig.4 Projection drawing of HRRP sequence

提取圖4中各個成像時刻目標的幅值，得到目標一維距離像幅值序列如圖5所示。

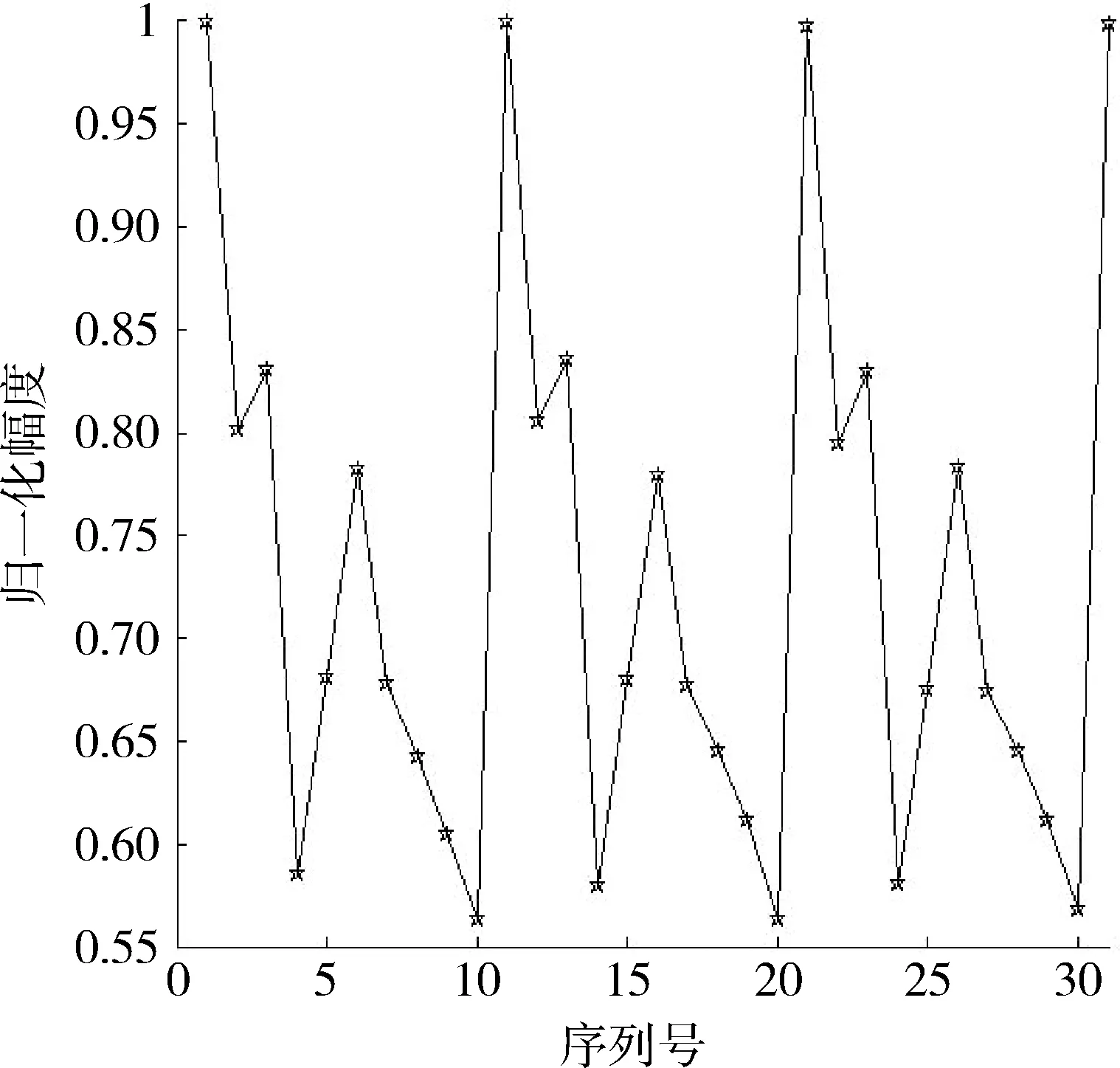
圖5 幅值軌跡圖Fig.5 Trajectory diagram of HRRP sequence’s amplitude

從圖5也可以看出，其幅值序列軌跡不規則，利用傳統的最小二乘擬合的多項式擬合，即使擬合階數很高，誤差仍然很大。

按照本文的提出的進動周期估計方法，取門限ξ2為0.05，已知慢時間采樣間隔為0.1 s，容易算得σ<ξ2，并可估計周期值為1 s，與仿真參數設置的進動頻率fc對應，估計效果較好。

信噪比為-10 dB時，成像序列投影圖如圖6所示。

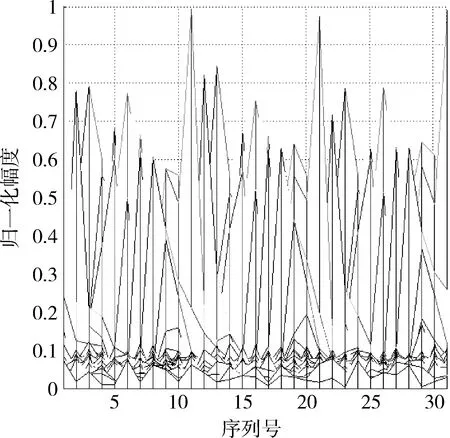
圖6 SNR為-10 dB時的成像序列投影圖Fig.6 Projection drawing of HRRP sequence while SNR=-10 dB

從上圖6的成像序列結果可以看出，雖然其周期性不再嚴格，但是在一定的門限ξ2(取為0.1)，仍可認為具有周期性并估計出其進動周期。說明本文的成像序列進動周期提取算法，在低信噪比時仍有較好的效果。

5 結束語

目標進動特征的提取是彈道導彈防御系統中段目標識別的重要手段。本文在忽略自旋對散射中心的調制和不發生散射中心遮擋的假設下，建立圓環邊緣滑動散射點模型，提出了一種基于一維距離像序列的進動周期提取算法，該方法依據一維距離像序列的周期性來反演進動周期，并根據所得成像序列，提出一種新的進動周期估計方法。實際中，對于結構復雜的有翼彈道目標及考慮遮擋時，分析過程更為復雜，方法需進一步完善。

[1] LEI P, WANG J, SUN J. Analysis of Radar Micro-Doppler Signatures from Rigid Targets in Space Based on Inertial Parameters[J]. IET Radar Sonar and Navigation，2011，5(2): 93-102.

[2] 田巳睿，蔣躍紅，郭汝江，等. 基于時頻變換的彈道目標微多普勒特征提取[J]. 現代雷達，2012，34(1): 40-43,48. TIAN Si-rui, JIANG Yue-hong, GUO Ru-jiang, et al. Ballistic Target Micro-Doppler Feature Extraction Method Based on the Time-Frequency Analysis[J]. Modern Radar，2012，34(1): 40-43,48.

[3] CHEN V C, FAYIN L, SHEN-SHYANG H, et al. Micro-Doppler Effect in Radar: Phenomenon, Model, and Simulation Study[J]. IEEE Transactions on Aerospace and Electronic Systems, 2006, 42(1): 2-21.

[4] 李松，馮有前，劉昌云，等. 彈道導彈微動模型及微多普勒特征研究[J]. 現代防御技術，2011,39(6)：95-99. LI Song，FENG You-qian，LIU Chang-yun，et al. Research of Micro-Motion Model and Micro-Doppler of Ballistic Missile[J]. Modern Defence Technology，2011,39(6)：95-99.

[5] 周萬幸．彈道導彈雷達目標識別技術[M]. 北京：電子工業出版社，2011． ZHOU Wan-xing. BMD Radar Target Recognition Technology[M]. Beijing: Publishing House of Electronics Industry，2011.

[6] 胡杰民，付耀文，黎湘. 空間錐體目標進動周期估計[J]. 電子與信息學報，2008，30(12): 2849-2853. HU Jie-min，FU Yao-wen，LI Xiang. Precession Cycle Estimation of Cone-Shaped Spatial Target[J]. Journal of Electronics & Information Technology，2008，30(12): 2849-2853.

[7] 羅迎，柏又青，張群,等. 彈道目標平動補償與微多普勒特征提取方法[J]. 電子與信息學報，2012，34(3): 602-608. LUO Ying，BAI You-qing，ZHANG Qun，et al. Translational Motion Compensation and Micro-Doppler Feature Extraction of Ballistic Targets[J]. Journal of Electronics & Information Technology，2012，34(3): 602-608.

[8] GHALEB A, VIGNAUD L, NICOLAS J M. Micro-Doppler Analysis of Wheels and Pedestrians in ISAR Imaging[J]. IET Signal Processing，2008，2(3):301-311.

[9] THAYAPARAN T, STANKOVIC L, DJUROVIC I. Micro-Doppler-Based Target Detection and Feature Extraction in Indoor and Outdoor Environments[J]. Journal of Franklin institute，2008(6): 700-722.

[10] 李松，馮有前，劉昌云，等. 彈道導彈微動模型及微多普勒特征研究[J]. 現代防御技術，2011，39(6):95-99. LI Song,FENG You-qian,LIU Chang-yun,et al. Research of Micro-Motion Model and Micro-Doppler of Ballistic Missile[J]. Modern Defense Technology，2011，39(6): 95-99.

[11] 劉進. 微動目標雷達信號參數估計與物理特征提取[D]. 長沙: 國防科學技術大學，2010. LIU Jin. Radar Signal Parameter Estimation and Physical Feature Extraction of Micro-Motion Targets[D]. Changsha: National University of Defense Technology，2010.

[12] 保錚，邢孟道，王彤．雷達成像技術[M]．北京：電子工業出版社，2005． BAO Zheng, XING Meng-dao, WANG Tong. Radar Imaging Technology[M]. Beijing: Publishing House of Electronics Industry，2005.

Precession Period Extraction of Ballistic Targets Using HRRP Series

HE Xing-yu1，TONG Ning-ning1，HU Xiao-wei1，CHEN Zhen-yu2

(1.AFEU，Air and Missile Defense School,Shaanxi Xi’an 710051, China；2.PLA,No.95784 Troop，Sichuan Chengdu 614100，China)

Precession is the inherent property of midcourse ballistic warheads. It is of great meaning to recognize the midcourse relying on the extraction of precession period both theoretically and practically. Firstly, the modeling of midcourse warheads’ cirque edge glide scattering centers is built and its coordinate representation are presented. Then, the HRRP series is obtained by controlling slow-time interval with dechirping method, and the imaging results are obtained in different attitude angles. Finally, the characteristics of HRRP series are analyzed and a new algorithm is presented to estimate the precession period. Simulation shows that the method has an effective and accurate performance in extracting targets’ precession period.

precession; scattering center; imaging series; period; estimation

2014-08-13；

2014-09-02

國家自然科學基金(61372166)

何興宇(1989-)，男，河北行唐人。碩士生，研究方向為雷達信號處理。

10.3969/j.issn.1009-086x.2015.04.036

TN953；TP391.9

A

1009-086X(2015)-04-0215-05

通信地址：710051 陜西省西安市長樂東路甲字1號空軍工程大學防空反導學院研2隊

E-mail：hxy_19890708@163.com