基于CFD 的混凝土輕舟船型阻力性能優化
葛 斌,胡堅城,黃蘊鈺,章 顏
(同濟大學 土木工程學院,上海200092)
0 引言
混凝土輕舟是ASCE主辦的美國賽中提出的一項比賽課題,在限定其長度不得超過6.7 m,寬度不得超過0.9 m的前提下,進行雙人、4人200 m或600 m劃行等比賽,從速度、密度、轉角靈敏度、穩定性等幾個方面衡量混凝土輕舟性能。
本文以2014年同濟大學混凝土輕舟隊在ASCE混凝土輕舟賽中的參賽輕舟為優化對象,欲在現有基礎上對輕舟的船型做進一步改進。影響輕舟速度、密度、靈敏度和穩定性等幾大性能的主要因素有船型、船重、水流條件等[1],其中船型是重中之重,而阻力最小的船體外形確定又是船型設計首先要追求的目標[2—4]。影響船型阻力的因素可分為橫剖面面積、設計水線、橫剖面形狀、船首船尾形狀等,而本文將以船長、型寬和最大橫剖面位置作為研究對象。
1 船舶設計理論分析
1.1 主要技術性能的分析
輕舟比賽是一項競速性比賽,船型對耐波性與穩定性的要求不高,而對快速性提出了極高的要求,因而設計時主要考慮船體的快速性。解決快速性問題主要是選擇合適的主尺度,優化船型,降低渦流阻力(形狀阻力)[1]。
在船型設計中,影響快速性的因素主要有:長寬比、最大橫剖面位置、橫剖面形狀以及船首船尾的構造。由于本文只限于二維船型設計分析,故以船長、型寬與最大橫剖面位置為主要研究對象。
1.2 主尺度的考慮與選擇
1.2.1 統計分析與初步選擇
首先,作者對其他各參賽學校的從2000年—2013年共75艘船型進行了研究與統計,關注的重點在于船長、型寬與長寬比。統計發現,各學校采用的船型尺寸在一定范圍內變化,特別是取得優異成績的船型主尺度具有一定規律。可得出以下結論:
(1)排名靠前的船長L:6.0~6.8 m;排名靠前的型寬B:0.66~0.81 m。
(2)L/B的取值在8.0~8.8較合適;當L/B>10.0時,普遍成績較差。
這些數值是基于10多年的參賽學校的成績統計值,因此具有一定的可靠性,本文所研究的范圍尺度也是在此基礎上。但由于此范圍較寬泛,為獲取更精確的值,本文進行了深入的理論分析。
1.2.2 船長的確定
考慮到船身越長,造價越高,且轉彎性能越差,而比賽中彎道所耗費的時間約占總耗時的1/3。為了減少轉彎帶來的不利影響,決定在上述結論上選擇最小船長作為研究對象,即選定船長為6 m。
1.2.3 型寬和最大橫剖面位置的確定
1.2.3.1 型寬B
(1)傅汝德數Fn
根據以往的比賽成績,排名靠前的輕舟劃行200 m直線距離所需時間t一般為90~120 s。可得傅汝德數的范圍為其中,g為重力加速度,g=9.8 m/s2。設計時取t為105 s,則 Fn=0.255。
(2)方形系數Cb
由方形系數的估算公式(亞歷山大公式適用于Fn <0.30)[1]可得:Cb=0.63。
(3)長寬比L/B
由方形系數Cb確定長寬比 L/B[1]:L/B≈6.8。則B=0.88 m。
1.2.3.2 最大橫剖面位置
根據已有的優良型線面積曲線的一般特性,對經驗公式進行修正后可得到適宜的進流段長度公式:

式中:LE為進流段長度,Lpp為船長,CP為棱形系數,Cp=Cb/Cm(Cm為中橫剖面系數補充)[1]。
根據文獻[1],Cb、Cm與 Cp的關系曲線圖可得Cp約為0.63~0.66,故 LE/Lpp=0.525~0.542。
因而進流段長度LE=3.15~3.25 m,也即最大橫剖面位置位于中點偏后0.15~0.25 m。
顯然L/B=6.8的結論與上文中的長寬比適宜范圍相差較遠。這是由于經典船舶設計理論中的型線設計考慮因素較綜合,沒有突出快速性的要求,因此本文尋找的最優寬度與最大橫剖面位置可能與上述結論存在出入。本文擬使用CFD方法進行數值模擬,以期得到一個更優的選擇。
2 船型優化思路
2.1 基本假定
(1)對于船舶粘性繞流來說,根據運動的相對性原理,輕舟在靜水中劃行時,可等效為輕舟靜止而水流以舟的速度流動。兩邊的河岸可設為管道壁,轉化為流體在管道中的流動問題。
(2)將輕舟的劃行看成勻速,即忽略人員劃槳的不連續性,故可將水流設為勻速。
(3)由于轉彎時分析較為復雜,故本文只考慮輕舟在直線劃行時的數值模擬。
(4)忽略輕舟的操縱難易程度,只把輕舟劃行時產生的阻力作為唯一評判指標。
(5)忽略由于寬度和最大橫剖面位置改變所引起的設計水線的變化。
(6)由于本文只考慮二維船型,即船長、船寬、最大橫剖面位置這幾個參數。而船長L經上文分析已確定,結合對往年各參賽船型的分析,得到型寬的范圍B=0.66~0.81 m。由經驗分析得到的最大橫剖面位置X=3.15~3.25 m,在建模時將范圍放大至X=3.0~3.30 m,對這2個參數進行組合得到以下24個不同模型進行二維建模:
船寬 B:0.66、0.69、0.72、0.75、0.78、0.81 m。最大橫剖面位置 X:3.0、3.1、3.2、3.3 m。
2.2 船型設計
本文以2014年同濟大學混凝土輕舟隊在美國ASCE混凝土輕舟賽中比賽用船作為優化對象。該船的船長6.19 m,型寬0.68 m,最大橫剖面位置距離船頭約3.4 m。該船的船型如圖1所示。

圖1 2014年ASCE混凝土輕舟賽同濟大學參賽船只
在大部分區段,該船的兩側壁垂直于水面,因此符合本文的基本思想,這為本模型得出較精確的解提供了保障。
通過Freeship等船型設計軟件,可以調整船型,并獲取船壁上任意點的坐標。通過一定的運算法則,可以將6.19 m的船型等效為6.0 m的船型;通過改變寬度及最大橫剖面的位置,可以得到不同的船型,從每個船型的船舷中選取20個控制點用于建模。以X=3.0 m,B=0.66 m時的船型曲線為例,如圖2所示。

圖2 X=3.0 m時的船型曲線
3 網格建立
本文中使用的網格由 GAMBIT軟件生成。GAMBIT是fluent的專業前處理軟件,生成的網格可直接導入fluent計算,其能夠生成結構和非結構2類網格。本文模型采用非結構化網格劃分方式,面網格采用Tri-Pave劃分方式。邊界層共設4層,第1層為0.05。網格的尺寸及劃分結果如圖3所示。
4 數值方法和理論計算
4.1 控制方程
流體流動符合質量守恒、動量守恒和能量守恒3大基本守恒定律。如果流動處于湍流狀態,系統還要遵守附加的湍流控制方程。控制方程是這些守恒定律的數學描述[5]。
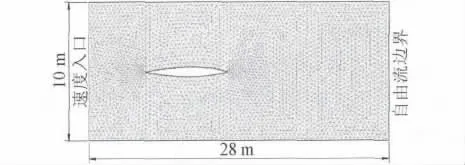
圖3 網格劃分結果
4.2 湍流模型
本文選用標準k-ε模型,具有數值穩定性好、求解壓力梯度精確等優點,是目前船舶粘性流動和粘性水動力求解應用最廣泛的湍流模型。
4.3 邊界條件
(1)入流邊界條件:速度入口(velocity inlet),模擬水流速度為2.3 m/s。
(2)出流邊界條件:由于控制域出口處離船尾部較遠,經過初步計算后發現出口處來流未受到船體的擾動影響,故可設為自由流邊界(outflow)。
(3)船體:設為無滑移壁面(wall)。考慮壁面粗糙度。
4.4 數值方法
4.4.1 方程離散
有限體積法(FVM)考慮在體積元邊界流出的矢通量等于相鄰體積元在該邊界流入的矢通量,從而保證了差分格式的守恒,因而即使在網格比較粗的情況下也能準確地顯示出積分守恒。同時FVM能采用各種形狀的網格以適應各種形狀的邊界幾何形狀。fluent軟件采用它來進行離散求解。
4.4.2 求解算法
本文采用SIMPLEC算法進行壓力-速度的耦合求解。離散格式均采用二階精度格式。
5 數據分析
從圖4、圖5可以得出以下2點結論:
(1)當型寬相同的情況下,以0.72 m為例,隨著最大橫剖面位置從船中3.0 m的位置往船尾移動,總阻力是先減小后增大,在3.2 m附近的位置減到最小。船寬為0.75、0.72、0.69、0.66 m時都基本符合上述規律,而0.81、0.78 m時結論有偏差。導致偏差的原因可能有:數值計算的系統誤差;當型寬較大時(如大于0.78 m),在3.2 m附近總阻力最小的結論不滿足。
(2)當最大橫剖面位置相同時,隨著型寬的增大,總阻力逐漸增大。

圖4 最大橫剖面位置與總阻力的關系
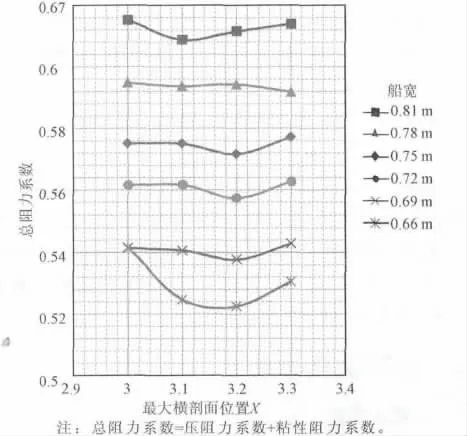
圖5 最大橫剖面位置與總阻力系數的關系
為了保證網格劃分的質量,作者對24個模型的壁面Yplus進行了統計(見圖6),發現均在53~55之間,說明模型網格劃分質量良好。
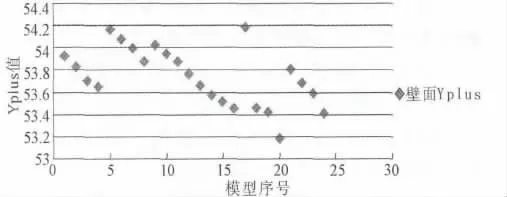
圖6 Yplus值
總結可得出以下結論:
(1)當型寬小于0.78 m時,最大橫剖面位置X=3.2 m時船體所受總阻力最小。
(2)型寬越大,總阻力越大,當B=0.66 m時,總阻力最小。
6 結論
本文通過統計分析、經典船舶設計理論分析與fluent軟件模擬等多方面分析,通過對復雜外形船體的二維模型建立,在船舶設計過程中優化船舶阻力的性能。從計算結果分析,得到如下2點結論:
(1)通過fluent數值模擬結果可知,優化后的船型最大橫剖面位置約為3.20 m處,此時總阻力最小,與經典船舶設計理論計算所得的3.15~3.25 m處吻合。
(2)在一定范圍內,長寬比L/B與快速性成正相關[1]。而在1.2.1的統計結果中對L/B有一定限制范圍,這是由于當L/B過大時,會對船體的穩定性造成較大影響。可取L/B=8.8,則優化后的船寬宜選0.68 m。
[1] 顧敏童.船舶設計原理[M].上海:上海交通大學出版社,2001.
[2] 馬坤,田中一朗.最小阻力船型優化研究[J].水動力學研究與進展,1997,12(1):113-122.
[3] 陳京普,朱德祥,何術龍.雙體船/三體船興波阻力數值預報方法研究[J].船舶力學,2006,10(2):23-29.
[4] 酈云,盧曉平.高速三體船阻力性能研究[J].船舶力學,2007,11(4):191-198.
[5] 周美,邢殿錄.流體力學[M].大連:大連理工大學出版社,2003.

