利用移動最小二乘法進行點云變形分析的研究

呂志鵬，伍吉倉,2，鄭二龍

(1.同濟大學測繪與地理信息學院，上海 200092； 2.現(xiàn)代工程測量國家測繪地理信息局重點實驗室，上海 200092)

?

利用移動最小二乘法進行點云變形分析的研究

呂志鵬1，伍吉倉1,2，鄭二龍1

(1.同濟大學測繪與地理信息學院，上海 200092； 2.現(xiàn)代工程測量國家測繪地理信息局
重點實驗室，上海 200092)

三維激光掃描儀能夠高精度快速翔實地獲得變形體的空間信息，同時諸多變形體的變形情況也需要完整的描述和分析。為此，本文通過三維激光掃描儀獲取變形體變形前后的點云數(shù)據(jù)，并利用移動最小二乘法進行均勻格網(wǎng)擬合內(nèi)插來提取變形信息。通過模擬簡支梁加載試驗和上述方法進行變形分析，并與TS30高精度測量機器人的測量結(jié)果進行對比，結(jié)果表明兩者精度相當，能夠探測到毫米級變形。

三維激光掃描儀；點云；移動最小二乘法；變形分析；TS30

一、引 言

對各種建筑物、構筑物及山體滑坡等自然災害頻發(fā)區(qū)的變形監(jiān)測是測繪領域的一項重要任務。從傳統(tǒng)的大地測量技術到GNSS技術，變形監(jiān)測的理論和方法已得到了廣泛而深入的研究。然而，這些觀測技術本質(zhì)上屬于基于點的測量方式，也就是說將變形體的變形特征用一些特征點進行離散化，然后通過測量這些特征點的空間位置變化來反演變形體的變形情況。它們的缺陷在于：一方面用有限的特征點反演變形體變形情況是否可靠仍值得商榷；另一方面由于對特征點的高度依賴性，一旦特征點被破壞將影響變形監(jiān)測成果的連續(xù)性。三維激光掃描儀的出現(xiàn)則改變了傳統(tǒng)變形監(jiān)測作業(yè)模式，它是一種“面”測量設備，能夠高精度、高分辨率、高效率地以非接觸的方式獲得變形體表面的點云數(shù)據(jù)，能夠?qū)ψ冃误w的變形情況進行全面的描述。利用三維激光掃描儀獲取的點云數(shù)據(jù)進行變形分析已經(jīng)取得了一些成果[1-7]。這些方法主要是利用點云數(shù)據(jù)擬合特征點、線來進行變形分析，應用范圍具有局限性，不能達到對變形體的變形情況進行全面分析的目的。為此，本文利用移動最小二乘法擬合內(nèi)插均勻格網(wǎng)來進行變形分析，以實現(xiàn)對變形體變形特征的整體把握。

二、移動最小二乘法

變形體空間變形中一類重要的情況就是沿著垂直方向的變形，分析該類變形需要根據(jù)點云數(shù)據(jù)擬合二維曲面，移動最小二乘法即可以利用不規(guī)則的空間數(shù)據(jù)建立連續(xù)的二維曲面函數(shù)[8-12]。因此，可利用移動最小二乘法進行點云數(shù)據(jù)的均勻格網(wǎng)擬合內(nèi)插。對于三維激光掃描儀采集到的點云數(shù)據(jù)可以構造如下二維曲面函數(shù)，即

(1)

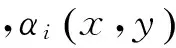
(2)

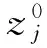
(3)

故有

(4)

其中

將式(4)代入式(1)可得

(5)

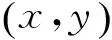
(6)

二維高斯函數(shù)圖像如圖1和圖2所示，二維高斯函數(shù)滿足上述權函數(shù)的緊支性要求。在圖2中可以清晰地看到若干同心圓，并且同心圓所對應的函數(shù)值隨其半徑的增大而減小。同時，在同心圓外側(cè)圖像原色趨于深藍色，其函數(shù)值趨近于0。

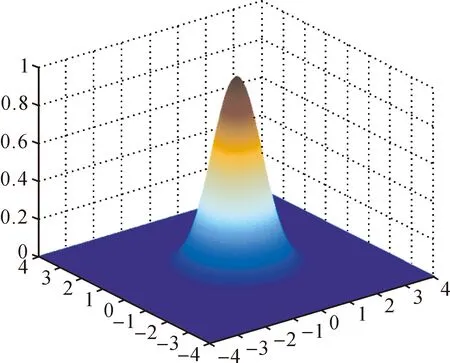
圖1 二維高斯函數(shù)圖像(h=1)

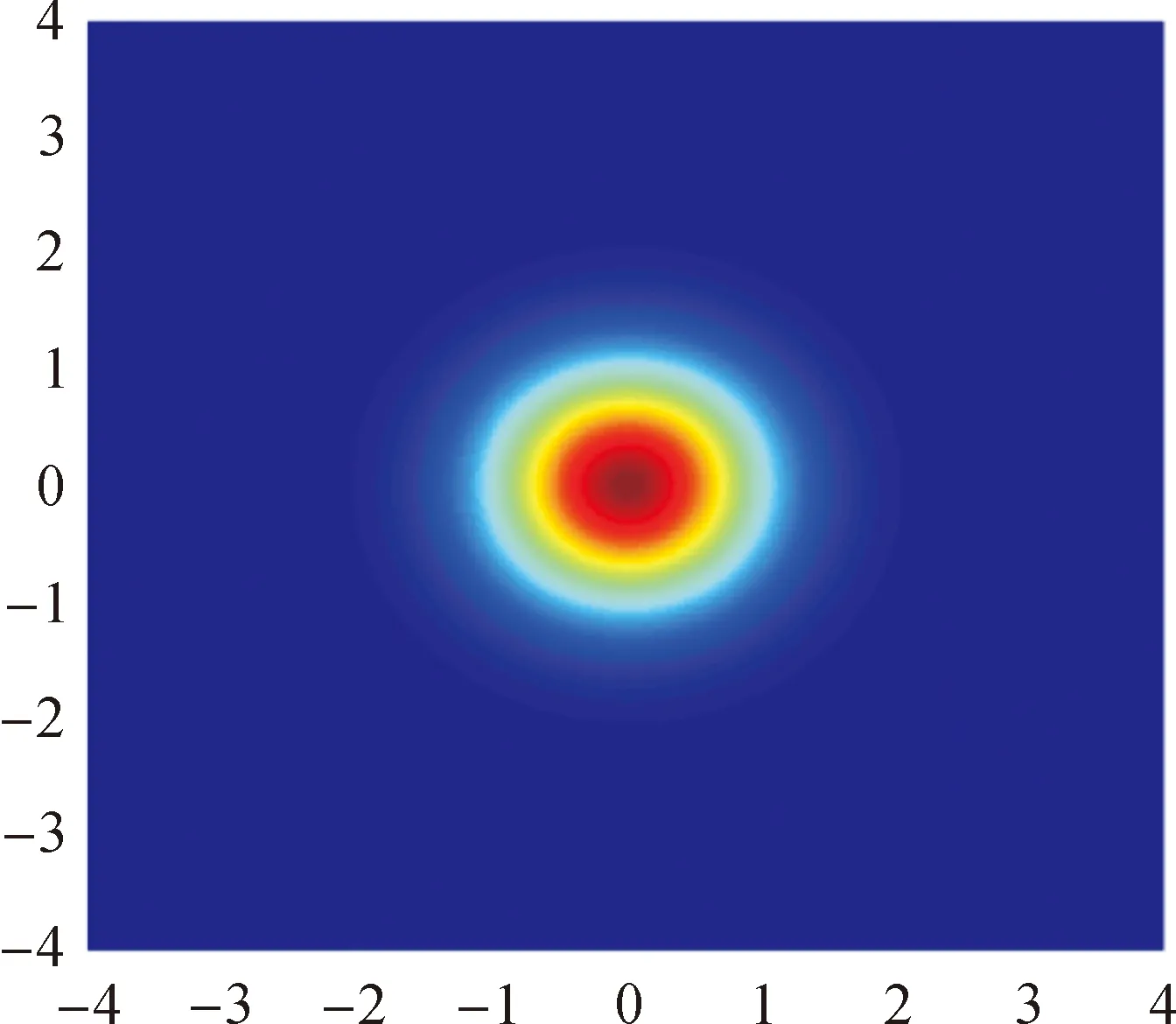
圖2 二維高斯函數(shù)圖像俯視圖

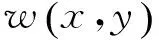
應用移動最小二乘法進行點云變形分析的一般流程如下：

1) 將變形前后的點云覆蓋范圍在水平面上進行相同的格網(wǎng)化。

2) 對于變形前后點云的每個格網(wǎng)點有：①根據(jù)權函數(shù)的影響域確定擬合點集；②根據(jù)式(4)和式(5)計算格網(wǎng)點的函數(shù)值。

3) 將變形前后對應格網(wǎng)點的函數(shù)值相減獲得變形量。

三、試驗結(jié)果分析

本次試驗通過不銹鋼扁管(規(guī)格2200 mm×80 mm×30 mm)中部受壓模擬簡支梁的加載變形過程(如圖3所示)。利用FARO Focus3D掃描儀在不銹鋼扁管受壓前后掃描其上頂面和正對掃描儀側(cè)面的點云數(shù)據(jù)，掃描采用最高分辨率和最優(yōu)掃描質(zhì)量。同時在不銹鋼扁管正對掃描儀側(cè)面粘貼15個平面靶紙。在不銹鋼扁管懸掛重物前后用Lecia TS30測量機器人(測角精度：0.5″，測距精度：0.6 mm+1×10-6D)測量15個平面靶紙的中心坐標，獲取不銹鋼扁管加載后的變形曲線。

圖3 扁管中部受壓試驗

圖3是不銹鋼扁管中部受壓試驗實物圖。不銹鋼扁管中部1.8 m的范圍(第一個到最后一個平面靶紙中心的距離)懸空。在試驗過程中首先在空載條件下掃描點云數(shù)據(jù)，然后在0.90 m處懸掛重物再進行掃描。掃描前后提取的不銹鋼扁管頂部點云如圖4和圖5所示。

圖4 受壓前扁管頂部點云

圖5 受壓后扁管頂部點云

在不銹鋼扁管伸展方向的0、0.15 m、0.30 m、0.45 m、0.60 m、0.75 m、0.825 m、0.90 m、0.975 m、1.05 m、1.20 m、1.35 m、1.50 m、1.65 m、1.80 m處粘貼平面靶紙。在加載前后用TS30分別測量15個平面靶紙的中心坐標。測量過程中建立獨立坐標系，坐標成果及變形量見表1。由表1可知，不銹鋼扁管的變形基本呈現(xiàn)對稱的特性，在加載點8號點處呈現(xiàn)出最大的變形量為15.5 mm，在兩端變形量最小，約為1.7 mm。

在利用移動最小二乘法進行均勻格網(wǎng)內(nèi)插時，需要將受壓前后扁管頂部點云從儀器坐標系轉(zhuǎn)換到變形體坐標系下。如圖6所示，oxyz為儀器坐標系，o′x′y′z′為變形體坐標系。實際上可以認為儀器坐標系的z軸和變形體坐標系的z′軸指向相同。因而，兩個坐標系之間變換可以簡化為儀器坐標系繞著z軸的旋轉(zhuǎn)和整體平移[15]。故有

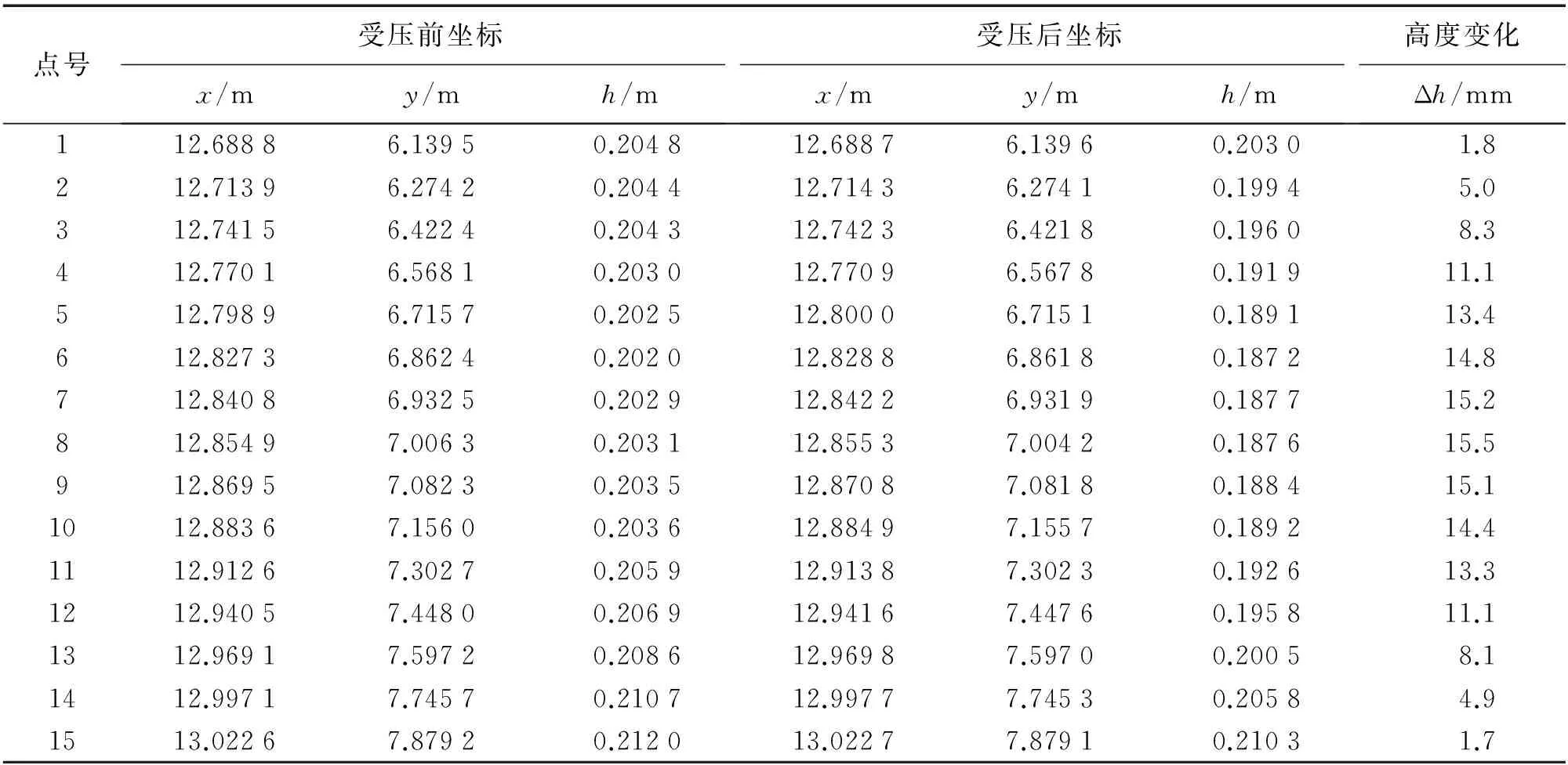
表1 扁管受壓前后平面靶紙中心坐標及其變化

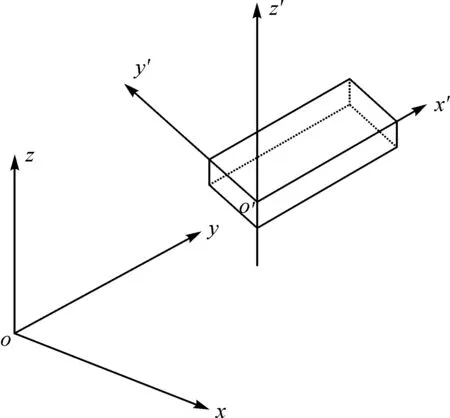
圖6 儀器坐標系和變形體坐標系關系

(7)

式中，(x,y,z)為儀器坐標系下坐標；(x′,y′,z′)為變形體坐標系下的坐標；(x0,y0,z0)為變形體坐標系的原點在儀器坐標系下的坐標，其確定了3個平移參數(shù)；γ為儀器坐標系繞z軸的旋轉(zhuǎn)角度。

提取出0和1.80 m處的平面靶紙的中心坐標，據(jù)此確定出儀器坐標系和變形體坐標系之間的旋轉(zhuǎn)角度為-0.025 1 rad，然后根據(jù)0處的擬合中心坐標及已知平面靶標內(nèi)圓的半徑為0.015 m確定平移向量為(0.900 5, -1.139 4, 0.550 9)。據(jù)此將不銹鋼扁管的頂部點云從儀器坐標系變換到變形體坐標系。

由上面的分析可知，不銹鋼扁管頂面的有效點云范圍是變形體坐標系x′o′y′面1.80 m×0.08 m范圍內(nèi)的點云。因此，首先將原始扁管頂部點云數(shù)據(jù)進行濾波降噪[16-17]并稀釋，得到加載前的點云數(shù)為13 489個，加載后的點云個數(shù)為14 392個；其次將點云根據(jù)式(7)從儀器坐標系變換到變形體坐標系；然后分別沿x′軸和y′軸方向每隔0.005 m獲得節(jié)點坐標形成均勻格網(wǎng)；最后用移動最小二乘法(式(6)中，h=0.005 m，采用1階完備多項式)內(nèi)插加載前后的均勻格網(wǎng)，按上節(jié)的方法獲得扁管表面垂直向的變形量，如圖7所示。

圖7 內(nèi)插均勻格網(wǎng)法變形圖

由圖7可知，不銹鋼扁管在受壓過程中整體上呈現(xiàn)對稱的變形特征。在中間的變形量最大，約為15 mm，在兩端的變形量最小，約為2 mm，這與TS30獲得的變形數(shù)據(jù)相吻合。同時可以看到，圖7中部區(qū)域呈現(xiàn)出微小的下深上淺特點，這與受壓時扁管頂面前后受力不均勻有關。在變形圖上邊緣處存在明顯的與整體不一致的變形趨勢，主要是因為這部分點云質(zhì)量不高，受到了掃描過程中邊緣效應的影響，特別是在右側(cè)上邊緣尤其嚴重。從圖3可以看出扁管后面偏右處是一黑色的椅子，激光束在掃描到扁管邊緣時，一部分返回到掃描儀而另一部分照射到反射特性并不明顯的椅子上造成較大邊緣效應誤差。

如圖8所示，獲取均勻格網(wǎng)在點(0, 0)、(0.15, 0)、(0.30, 0)、(0.45, 0)、(0.60, 0)、(0.75, 0)、(0.825, 0)、(0.90, 0)、(0.975, 0)、(1.05, 0)、(1.20, 0)、(1.35, 0)、(1.50, 0)、(1.65, 0)、(1.80, 0)處扁管在垂直方向的變形量，將其與TS30獲得的平面靶紙中心z坐標變化進行比較，兩者的變形趨勢整體一致，最大互差為0.9 mm，互差的均方差為0.4 mm，說明兩者具有良好的一致性。

四、結(jié)束語

三維激光掃描儀是一種“面”測量設備，能夠高精度、高密度、高速度地獲取變形體表面的空間信息，詳細描述變形體表面細部特征。本文應用移動最小二乘法擬合內(nèi)插均勻格網(wǎng)獲取變形量并形成變形面，更加詳細地描述了變形體的變形情況。同時，通過與TS30高精度測量機器人獲取的變形結(jié)果進行比較發(fā)現(xiàn)，兩種方法的變形量互差均方差僅為0.4 mm，具有良好的一致性。因而可以說，利用三維激光掃描儀探測毫米級變形具有可行性。三維激光掃描儀在高精度獲取變形體的整體變形趨勢方面應用前景廣闊。

圖8 變形量對比圖

[1] 徐進軍, 王海城, 羅喻真, 等.基于三維激光掃描的滑坡變形監(jiān)測與數(shù)據(jù)處理[J].巖土力學, 2010, 31(7): 2188-2191.

[2] 戴華陽, 廉旭剛, 陳炎, 等.三維激光掃描技術在采動區(qū)房屋變形監(jiān)測中的應用[J].測繪通報, 2011(11): 44-46.

[3] 王延亮, 夏國芳, 胡春梅.利用三維激光掃描技術進行工業(yè)設備三維重建及變形分析[J].測繪通報, 2012(2): 94-96.

[4] 黃曉陽, 欒元重, 閆勇, 等.基于三維激光掃描測量技術的井架變形觀測[J].工程勘察, 2012, 40(4): 66-69.

[5] 劉云廣.基于地面三維激光掃描的變形監(jiān)測點分析[J].北京建筑工程學院學報, 2013, 29(2): 43-48.

[6] 吳侃, 黃承亮, 陳冉麗.三維激光掃描技術在建筑物變形監(jiān)測的應用[J].遼寧工程技術大學學報：自然科學版, 2011, 30(2): 205-208.

[7] 畢俊, 馮琰, 顧星曄, 等.三維激光掃描技術在地鐵隧道收斂變形監(jiān)測中的應用研究[C]∥地理信息與物聯(lián)網(wǎng)論壇暨江蘇省測繪學會 2010 年學術年會論文集.南京：江蘇省測繪學會，2010.

[8] LANCASTER P, SALKAUSKAS K.Surfaces Generated by Moving Least Squares Methods[J].Mathematics of Computation, 1981, 37(155): 141-158.

[9] MAISURADZE G G, THOMPSON D L, WAGNER A F, et al.Interpolating Moving Least-squares Methods forFitting Potential Energy Surfaces: Detailed Analysis of One-dimensional Applications[J].The Journal of Chemical Physics, 2003, 119(19): 10002-10014.

[10] SCHAEFER S, MCPHAIL T, WARREN J.Image Deformation Using Moving Least Squares[J].ACM Transactions on Graphics (TOG)， 2006, 25(3): 533-540.

[11] AHN S H, YOO J, LEE B G, et al.3D Surface Reconstruction from Scattered Data Using Moving Least Square Method[C]∥ International Conference on Image Analysis and Processing.2005, 719-726.

[12] 曾清紅, 盧德唐.基于移動最小二乘法的曲線曲面擬合[J].工程圖學學報, 2004, 25(1): 84-89.

[13] LEVIN D.The Approximation Power of Moving Least-squares[J].Mathematics of Computation, 1998， 67(224): 1517-1531.

[14] PAULY M.Point Primitives for Interactive Modeling and Processing of 3D Geometry[M].[S.l.]: Hartung-Gorre, 2003.

[15] 施一民.現(xiàn)代大地控制測量[M].北京：測繪出版社，2003.

[16] TOMASI C, MANDUCHI R.Bilateral Filtering for Gray and Color Images[C]∥Sixth International Conference on Computer Vision.[S.l.]: IEEE, 1998: 839-846.

[17] FLEISHMAN S, DRORI I, COHEN-OR D.Bilateral Mesh Denoising[J].ACM Transactions on Graphics (TOG), 2003, 22(3): 950-953.

[18] 鄧念武，朱杰兵.全站儀在隧洞三維變形監(jiān)測中的應用研究[J].巖土力學，2003，24：158-161.

[19] 姜衛(wèi)平，劉鴻飛，劉萬科，等.西龍池上水庫GPS變形監(jiān)測系統(tǒng)研究及實現(xiàn)[J].武漢大學學報：信息科學版, 2012,37(8): 949-952.

On Point Cloud Deformation Analysis Using Moving Least Squares Method

LV Zhipeng，WU Jicang，ZHENG Erlong

呂志鵬，伍吉倉，鄭二龍.利用移動最小二乘法進行點云變形分析的研究[J].測繪通報，2015(7)：32-35.

10.13474/j.cnki.11-2246.2015.0205

2014-05-08

中美國際合作項目(2010DFB20190)；國家自然科學基金(41074019)

呂志鵬(1988—)，男，碩士生，主要研究方向為精密工程測量與變形監(jiān)測。E-mail: lvzhipeng2007@gmail.com

P237

：B

：0494-0911(2015)07-0032-04