Dirichlet空間上Toeplitz算子的乘積
馮麗霞
(1.西北大學數學與科學史研究中心,陜西 西安 710127;2.山西師范大學數學與計算機科學學院,山西 臨汾 041004)
Dirichlet空間上Toeplitz算子的乘積
馮麗霞1,2
(1.西北大學數學與科學史研究中心,陜西 西安 710127;2.山西師范大學數學與計算機科學學院,山西 臨汾 041004)
給出了Dirichlet空間上一個Toeplitz算子的共軛算子與另一個Toeplitz算子的乘積仍為Toeplitz算子的刻畫.并得到了Dirichlet空間上一個Toeplitz算子的共軛算子與另一個Toeplitz算子的乘積為零算子的充要條件.
Dirichlet空間;Toeplitz算子;共軛算子;乘積
1 預備知識
設D是復平面C上的單位開圓盤,dA表示D上正規化的面積測度.稱D上光滑函數f在范數
下,取閉包所得到的空間為Sobolev空間,記為S,則S是一個Hilbert空間,定義其上內積為
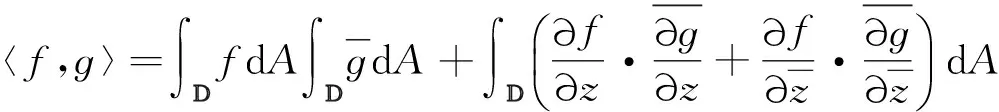
由S中所有滿足f(0)=0的解析函數構成的閉子空間稱為Dirichlet空間,記為D.
D上的一個非負測度μ稱為D-Carleson測度,如果存在非負常數c,使得
∫D|f|2dμ≤c‖f‖2,f∈D.
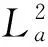
令

設φ∈M,則φ定義的D上Toeplitz算子Tφ為
Tφ(f)=P(φf),f∈D,
其中P是從S到D上的正交投影.容易驗證Tφ是D上的有界算子.一直以來,各種積分算子的有界性也是函數空間上算子理論的研究課題之一[1].
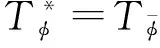
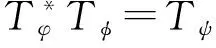
(1)φ=0,且ψ=0;
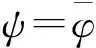
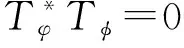
2 定理證明
下面引理表明,由S中的調和函數φ定義的Toeplitz算子Tφ在D上有界,當且僅當φ∈M.
引理1 設φ是S中的調和函數.如果Tφ在D上是有界的,則φ∈M.
證明 令
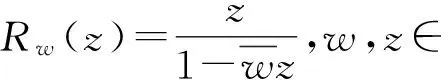
容易驗證:
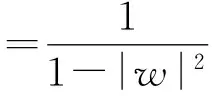
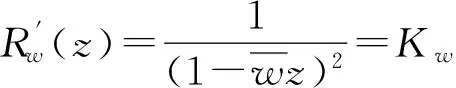
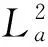
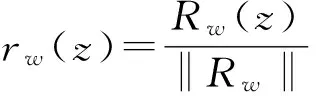
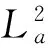
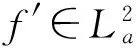
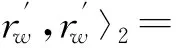
〈φ′rw,kw〉2+〈φkw,kw〉2=(1-|w|2)φ′(w)rw(w)+φ(w)=
w(1-|w|2)φ′(w)+φ(w)≤ω〈φ′,kw〉2+φ(w).
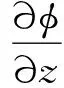
對任意f,ɡ∈D,
〈Tφf,ɡ〉=〈φf,ɡ〉=〈φ′f+φf′,ɡ′〉2=〈φ′f,ɡ′〉2+〈φf′,ɡ′〉2.
因為φ有界且Tφ有界,所以
|〈φ′f,ɡ′〉2|≤|〈Tφf,ɡ〉|+|〈φf′,ɡ′〉2|≤(‖Tφ‖+‖φ‖∞)‖f‖‖ɡ‖,
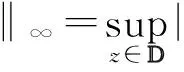

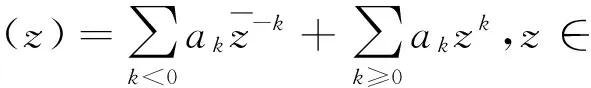
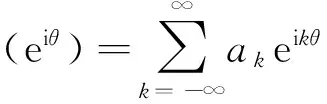
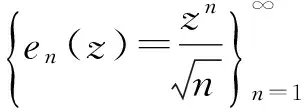
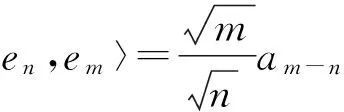
(1)
定理1的證明 充分性易驗證,我們只給出必要性的證明.
設
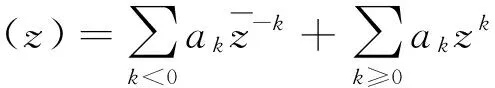
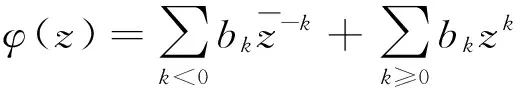
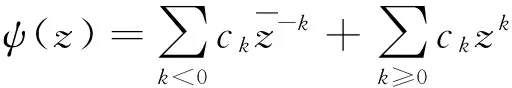
由(1)式,對于i,j≥1,
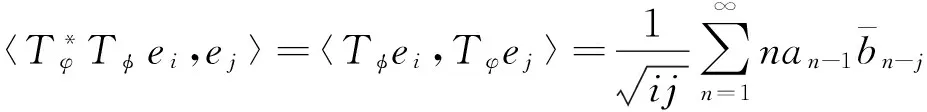
(2)
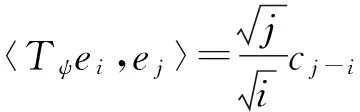
(3)
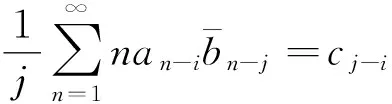
(4)
同理可得
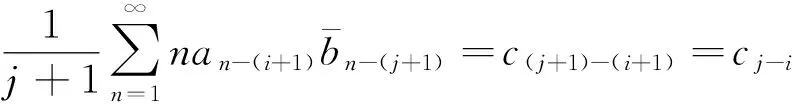
即
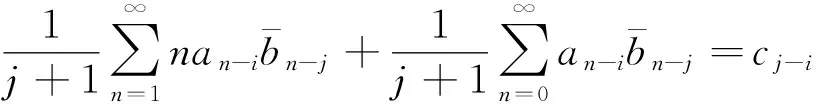
(5)
利用(4)和(5)式可知
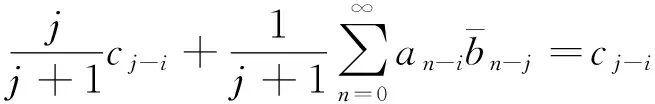
即
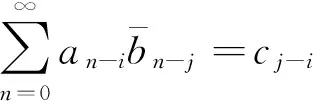
(6)
同時也有
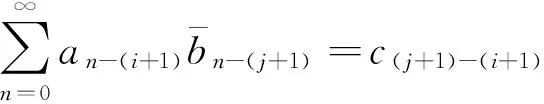
即
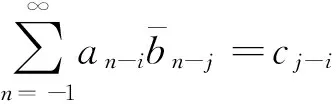
(7)
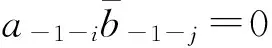
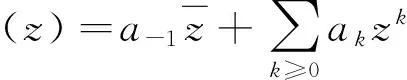
或
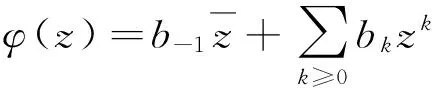
利用(4)與(6)式計算得
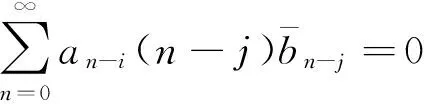
(8)
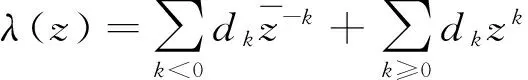
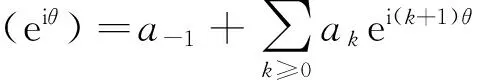
或
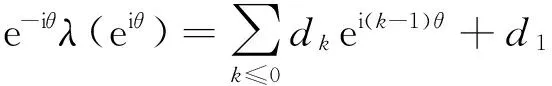
再由(8)式,
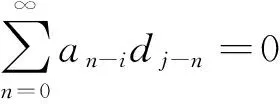
這表明eiθφ(eiθ)λ(eiθ)=0或e-iθφ(eiθ)λ(eiθ)=0,對幾乎處處的θ∈[0,2π]成立.由F.Riesz和M.Riesz定理[7]得φ=0或λ=0.
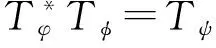
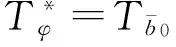
[1] 周淑娟.Marcinkiewicz積分在加權Hardy空間的有界性[J].東北師大學報(自然科學版),2015,47(2):21-24.
[2] CHEN Y,NGUYEN Q D.Toeplitz and Hankel operators with symbols on Dirichlet space[J].J Math Anal Appl,2010,369(1):368-376.
[3] LEE Y.Algebraic properties of Toeplitz operators on the Dirichlet space[J].J Math Anal Appl,2007,329(2):1316-1329.
[4] LEE Y.Finite sums of Toeplitz products on the Dirichlet space[J].J Math Anal Appl,2009,357(2):504-515.
[5] LEE Y,ZHU K.Sums of products of Toeplitz and Hankel operators on the Dirichlet space[J].Intergr Equ Oper Theory,2011,71(2):275-302.
[6] YU T.Toeplitz operators on the Dirichlet space[J].Integr Equ Oper Theory,2010,67(2):163-170.
[7] DOUGLAS R G.Banach algebra techniques in operator theory.2nd ed[M].New York:Springer-Verlag,1998:137.
(責任編輯:李亞軍)
Product of Toeplitz operators on the Dirichlet space
FENG Li-xia1,2
(1.Center for the History of Mathematics and Science,Northwest University,Xi’an 710127,China;2.School of Mathematics and Computer Sciences,Shanxi Normal University,Linfen 041004,China)
It is studied that the product of the adjoint of a Toeplitz operator and another Toeplitz operator can be a Toeplitz operator on the Dirichlet space under some conditions.As a corollary,we show that on the Dirichlet space,the zero product of the adjoint of a Toeplitz operator and another Toeplitz operator holds only for trivial symbols.
Dirichlet space;Toeplitz operators;conjugate operator;product
1000-1832(2015)04-0042-04
10.16163/j.cnki.22-1123/n.2015.04.009
2014-03-08
國家自然科學基金資助項目(11201274).
馮麗霞(1978—),女,博士,講師,主要從事泛函分析,數學史與數學教育研究.
O 177.1 [學科代碼] 110·57
A

