基于Gumbel Copula函數的金融高頻數據極大值相依性

霍俊爽，張若東，潘淑霞，邰志艷，董小剛

(1.吉林醫藥學院數學教研室，吉林 吉林 132013；2.長春工業大學基礎學院，吉林 長春 130012)

基于Gumbel Copula函數的金融高頻數據極大值相依性

霍俊爽1，張若東1，潘淑霞1，邰志艷1，董小剛2

(1.吉林醫藥學院數學教研室，吉林 吉林 132013；2.長春工業大學基礎學院，吉林 長春 130012)

基于Copula函數對股指期貨IF1112指數和上證000 001指數5 min極大值收益率序列的相依性進行了研究，探討了它們微觀結構的相依性.

Copula函數；Gumbel Copula函數；極值；相依性

伴隨著金融市場的全球化進程，金融市場間的相依性日趨緊密，一個金融市場的波動往往會迅速傳導至其他金融市場.本文從高頻數據極值這樣一個全新視角，研究不同金融市場高頻數據極值收益率變化的相依性，這對金融資產管理和風險控制具有良好的指導意義.

由于金融市場收益率的分布大多數呈現尖峰厚尾的形態，所以不能用正態分布或t分布來描述.而Copula函數在研究這類數據時有明顯優勢，本文將利用Gumbel Copula函數研究不同金融市場高頻數據極值的相依性.

1 模型方法與參數估計

1.1 Gumbel Copula函數與相依性分析

Gumbel Copula函數是二元阿基米德Copula函數族的一員，在金融數據的相依性分析中有著重要的應用[1-3].

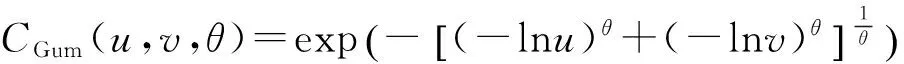
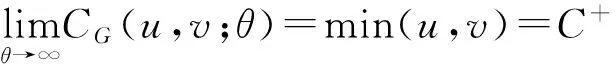
Gumbel Copula函數的密度函數呈非對稱性，具有“J”形分布.其上尾部高且下尾部低，下尾部相關性為零，它能較好地反映變量分布上尾部變化，使上尾部相關性的變化能夠被快速捕捉到，對牛市時期金融市場之間波動的變化規律有較好的描述.即兩個金融市場之間向上具有更強的相依性，而難以捕捉到下尾部相關變化.

1.2GumbelCopula函數的參數估計

Genest和Rivest[6]直接利用Kendall系數τ來估計阿基米德族Copula函數中的參數，而不需要求出邊緣分布函數.

設(x1，y1)，(x2，y2)，…，(xn，yn)為來自聯合分布H(x，y)的二元觀測值樣本，計算Kendall系數τ的無偏估計

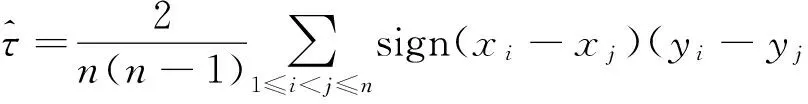
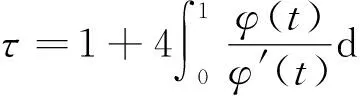
1.3 Copula模型的檢驗

常用的邊緣分布和Copula函數的檢驗方法有K-S檢驗、Q-Q圖檢驗和卡方檢驗.本文使用Q-Q圖檢驗，即分位數-分位圖檢驗，由變量的實際分布與變量的指定分布兩組樣本的分位數組成.若兩組樣本的對應分位數非常接近，則對應的Q-Q圖大致呈一條直線，可直觀形象地分析兩種分布的擬合情況；反之，偏離直線，擬合的就比較差.這種方法要求樣本容量要足夠大，否則影響結果的可靠性[7].

1.4 尾部相依性

尾部相依性能夠反映出當一個隨機變量暴漲或暴跌時，另一隨機變量也發生暴漲或暴跌的概率.由Copula函數的定義和性質，可以推導出尾部相依性Copula函數的表達式.正尾部相依性為

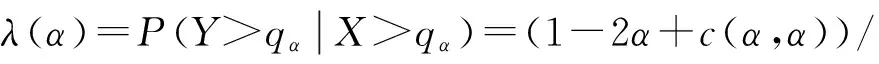
負尾部相依性為

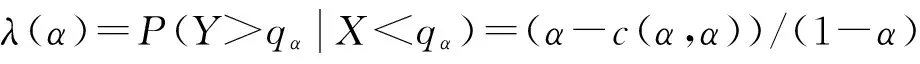
其中，α是概率，qα是相應于α的分位數.所以當α→1時，λU=2-2(1/θ)；當α→0時，λL=2(-1/θ).

2 實證分析

主要研究指數轉化為收益率的數據.選取2011年10月24日至11月18日股指期貨IF1112指數的5 min內最大值(GZD)和上證指數的5 min內最大值(SZD)數據.把每5 min內指數的最大值PT定義為價格，收益率定義為rt=100×ln(Pt/Pt-1).選取同期交易的數據構成兩個序列，每個序列有效數據1 200個.本文中使用了Eviews，SPSS，Matlab等軟件計算和繪圖.

2.1 極值收益率序列的波動圖

利用Eviews軟件計算并繪制極值收益率序列的波動圖，見圖1(橫坐標表示時間，每5 min為一個觀測點).

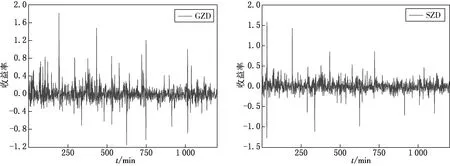
圖1 GZD和SZD收益率序列波動圖

從圖1中不難看出，對應的極值收益率序列波動具有一致性，即股指期貨的收益率序列上漲或下降時，對應的上證指數收益率序列也上漲或下降，并且有顯著的集群效應.初步說明我國股指期貨市場與股票市場之間的極值收益率序列之間有較強的相依性.針對各個序列統計分析可得其統計量，如表1所示.

表1 極值收益率序列的統計量

從極值收益率序列樣本的統計量不難看出：SZD收益率序列、GZD收益率序列都出現了右偏；SZD收益率序列、GZD收益率序列的J-B統計量分別為26 793.97，12 949.09，都拒絕了正態分布的假設.

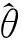
利用SPSS17.0軟件求得GZD與SZD收益率序列的相關系數τ=0.53，雙側檢驗的顯著概率小于0.01，相關性顯著.由τ與θ之間的關系計算參數θ=2.128.對于GZD與SZD收益率序列，參數θ在Gumbel Copula函數的參數定義域中.

2.3 檢驗Gumbel Copula函數

已求出參數θ的估計值，但是Gumbel Copula函數能否描述GZD與SZD收益率序列之間的相依性，還需檢驗.下面用均勻分布的Q-Q圖進行檢驗，結果見圖2.

從圖2中可以看出Q-Q圖大致呈一條直線，可直觀形象地分析兩種分布的擬合情況，說明Gumbel Copula函數非常適合描述最大值收益率序列的相依性.

2.4 尾部相關性

2.4.1 最優經驗分布散點圖

首先， 我們通過收益率序列最優經驗分布得到的序列散點圖，觀察一下對應極值的尾部相關性，見圖3.

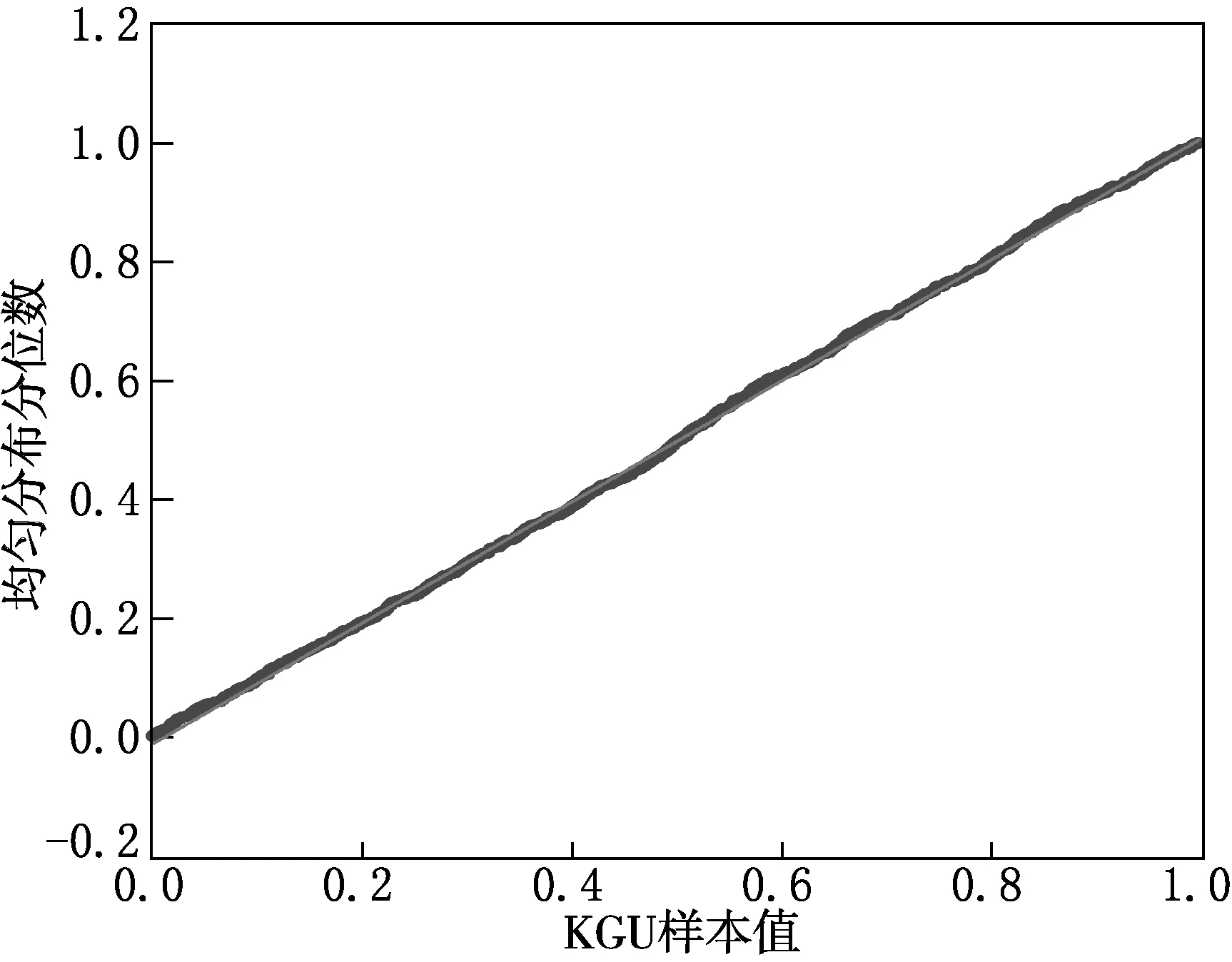
圖2 收益率的Gumbel Copula函數Q-Q圖檢驗

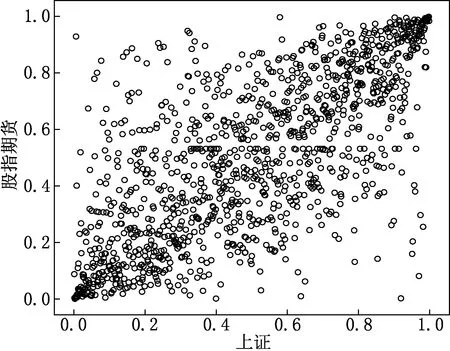
圖3 GZD與SZD對應收益率序列最優經驗分布散點圖

從圖3中我們可以看出GZD與SZD對應收益率序列最優經驗分布散點圖都具有很強的尾部相關性.

2.4.2 GZD與SZD收益率的相依性

利用Gumbel Copula函數計算上尾相關系數得：當α=0.925時，λU=0.635 3；當α=0.975時，λU=0.621 7；當α=0.995時，λU=0.616 3；當α→1時，λU= 0.615 0.

當GZD收益率超過q0.925，q0.975，q0.995時，SZD收益率超過對應的分位數的概率是0.635 3，0.621 7，0.616 3，都大于0.075，0.025，0.005，由此得出GZD與SZD收益率序列有很大的上尾部相依性.通過研究上尾部相依性，得到GZD收益率發生較大程度的波動時，SZD收益率發生大幅度變化的概率是很大的.

3 結論

通過實證研究我們發現，GZD與SZD收益率序列有很大的上尾部相依性.即GZD暴漲時，SZD的相依性會增強，但下跌時相依性減弱.此結論與股指期貨推出后我國股指期貨與上證指數之間的實際走勢基本吻合.從投資者投資行為上分析，可得其心理歷程：投資者看到股指期貨指數暴漲時，大多數投資者認為大部分投資者一致看好后市，都開始買入股票，從而使得上證指數也隨著暴漲；而股指期貨指數暴跌時，大多數投資者惜售從而導致上證指數不會暴跌，或暴跌滯后[8].

[1] GUMBEL E J. Bivariate exponential distributions [J]. Journal of American Statistical Association，1960，55:698-707.

[2] CLAYTON D G. A model for association in Bivariate life tables and its application in epidemiological studies of familial tendency in chronic disease incidence [J].Biometrika，1978，65:141-151.

[3] EMBRECHTS P，LINDSKOG C. Modeling dependence with copulas and applications to risk management [M]. Switzerland：Dept Math，2001：55-58

[4] FREES E W，VALDEZ E A. Understanding relationships using copulas[J].North American actuarial journal，1998，2(1):31-55.

[5] GENEST C，RIVEST L P. Statistical inference procedures for bivariate archimedean copulas [J]. Journal of the American Statistical Association，1993，88(423):1034-1043.

[6] HURLIMANN W. Fitting bivariate cumulative returns with copulas [J].Computational Statistics & Data Analysis，2004，45：355-372.

[7] ROCH O.Testing the bivariate distribution of daily equity returns using copulas：an application to the Spanish stock markert[J]. Computational Statistics & Data Analysis，2006，51:1312-1329.

[8] 鄭冬，梁錫坤.附加交易費用的動態投資組合魯棒策略[J].東北師大學報(自然科學版)，2014，46(2)：30-34.

(責任編輯：李亞軍)

Extreme interdependency of the high-frequency data in financial markets based on Gumbel Copula fuction

HUO Jun-shuang1，ZHANG Ruo-dong1，PAN Shu-xia1，TAI Zhi-yan1，DONG Xiao-gang2

(1.Department of Mathematics，Jilin Medical College，Jilin 132013，China；2.School of Basic Sciences，Changchun University of Technology，Changchun 130012，China)

Based on copula function，we mainly do the research on the dependency of the sequences yielded by 5 minutes maximum of index futures IF1112 and SSE 000 001.And explore the interdependence of their microstructure.

copula functions；gumbel copula function；extremum；interdependency

1000-1832(2015)04-0049-04

10.16163/j.cnki.22-1123/n.2015.04.011

2015-01-16

國家自然科學基金資助項目(11071026);吉林省教育廳“十二五”科學技術研究資助項目(2015393).

霍俊爽(1982—)，男，碩士，講師，主要從事應用數學與統計學研究；通訊作者：董小剛(1961—),男，博士，教授，主要從事應用數學研究.

O 212.1 [學科代碼] 110·2110

A