正弦機構在球面展開中的運用
龔凌云
(廣州鐵路職業技術學院機電工程學院,廣東廣州 510430)
1 引言
實現鋼球表面展開也就使鋼球在展開機構的作用下,連續、高速的運動,并將其表面各區完全的送到傳感器下進行檢測,在這一過程中球表面不能有盲區。鋼球表面展開運動實際上是鋼球受兩套獨立驅動機構的作用,完成一種比較復雜空間螺旋運動。本文利用正弦機構原理提出了一種新的球面運動展開方法。
2 正弦機構原理
正弦機構如圖1所示。在此機構中,從動件2與3(實為鋼球,其球心固定不動)只有滾動而無滑動,故為同步運動[1]。從動件2與原動件1的轉角α的正弦成正比,即
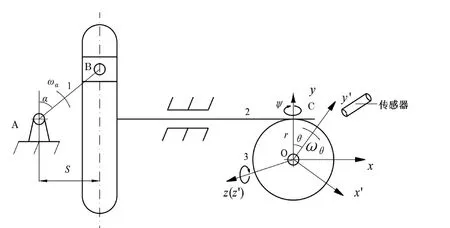
圖1 正弦機構

上式中, lAB為桿AB的長度,α為桿AB的轉角,ωα為桿AB的轉動角速度, t為轉動時間。對從動件3而言,則有:

上式中,r為球O的半徑,θ為球O的轉角。
由(2)式可得:

由此可知,當主動件1勻速轉動時,鋼球的轉角θ是按正弦規律變化的,轉角θ的最大值θmax取決于桿 AB的長度lAB與鋼球的半徑r,即
3 球面運動展開法
正弦機構實現了球繞Oz的來回偏轉,如果球同時繞Oy回轉,那么就能實現球體的偏轉,即也就實現球面的運動展開,即為球面的運動展開法。
鋼球在展開運動中,鋼球的球心O在空間的位置保持不變。選取O-xyz為固定坐標系,取O-x’y’z’為動坐標系與球固結,在初始位置與固定坐標系重合。如圖1所示。球繞固定坐標系Oy旋轉的同時,繞Oz旋轉,球繞Oy’與繞Oz’的轉角分別為ψ和θ。
鋼球在這整個運動過程中必須連續。因此,球對這兩個軸的轉動是有規律地定時重復,這樣球面上一點運動的軌跡曲線才能是閉合的[2]。在正弦機構的作用下,θ繞Oz’(Oz)規律做往復運動,即
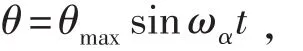
角速度大小
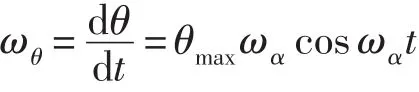
角速度矢量方向與OZ’(OZ)軸一致。轉角ψ為鋼球繞OY’軸在勻速運動時發生的轉角,即ψ=ωψt,ωψ為鋼球繞Oy/軸在勻速運動時的角速度,角速度矢量方向與Oy/軸一致。
鋼球上點的位置用矢量r表示,設半徑為R球面上一點P的初始坐標為(x0,y0,z0),經時間t變換后的坐標為(x,y,z)。則有

球面上P點的瞬時速度
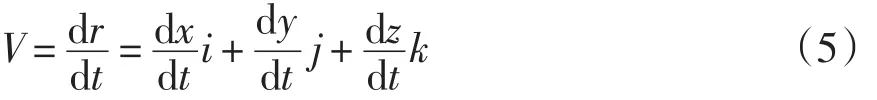
而
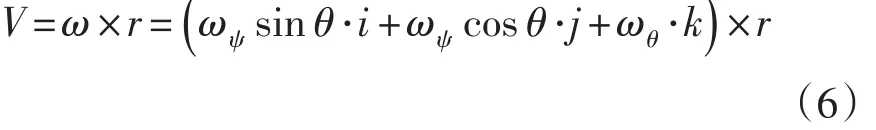
由以上二式得:
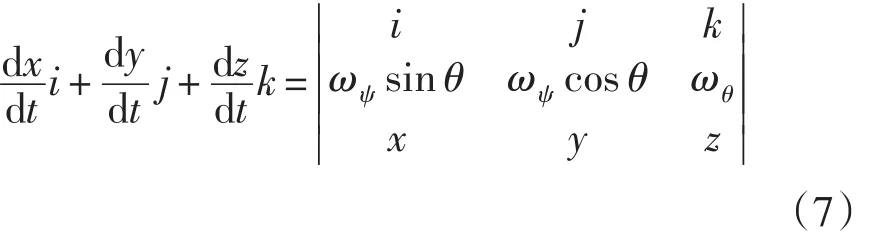
可知運動學方程為:

而動坐標系O-XYZ與靜坐標系O-X/Y′Z′之間的轉換矩陣為

球做自轉運動時,其上的任一點的坐標變換矩陣為

將(10)式代入(9)式,并引入初始解條件((x , y,z|t=0=(x0,y0,z0),可得P點運動的軌跡方程即

(11)式精確地給出了鋼球在正弦機構(ωα)與勻速運動機構(ωψ)綜合作用下,其上的一點P(x0,y0,z0經過時間t后,運動到球面上另一點(x,y,z)處的運動學方程。這一研究為鋼球展開機構的優化提供了必要的數學工具與理論基礎。
4 結論與實例
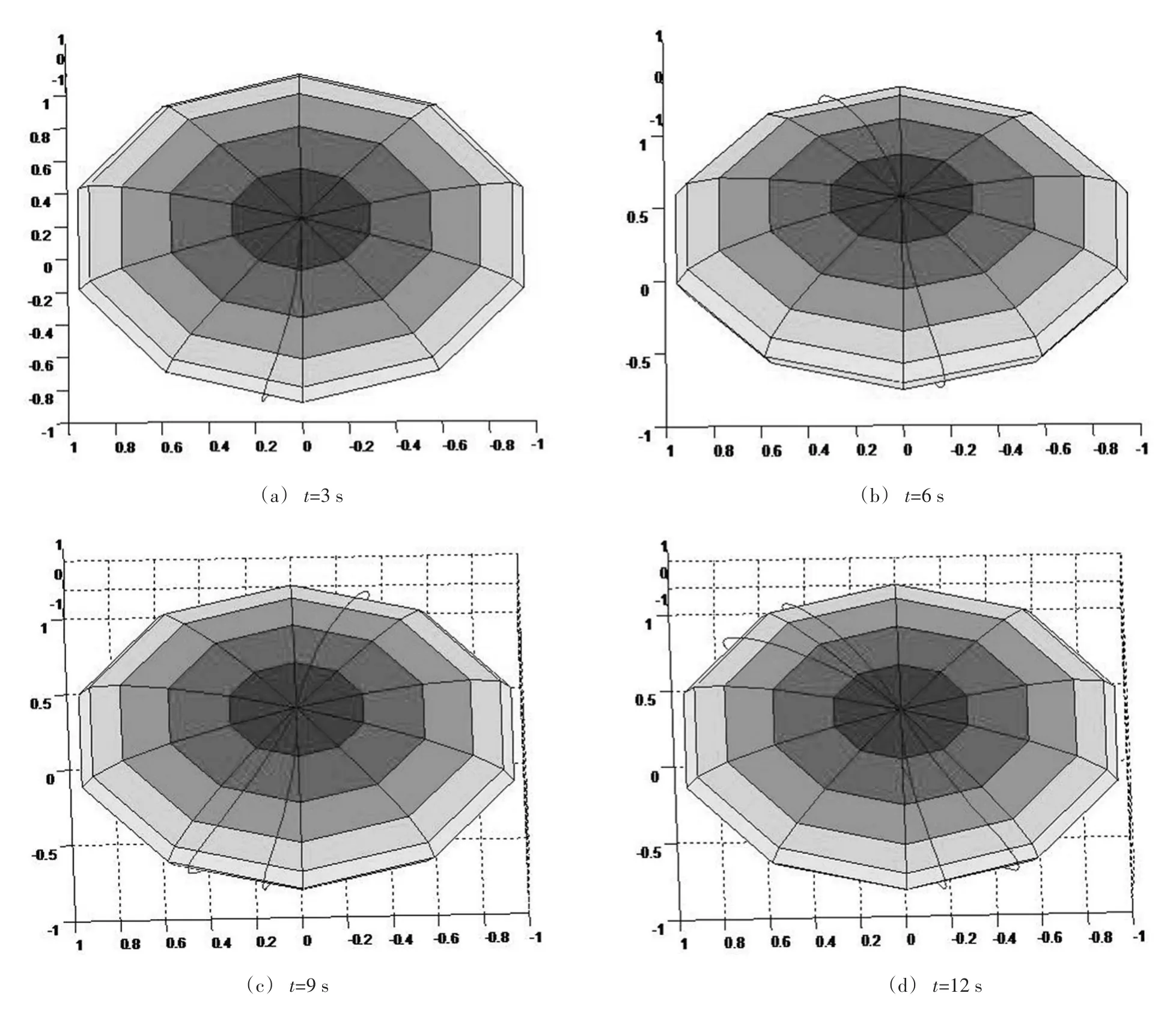
圖2 不同時刻P點的運動軌跡
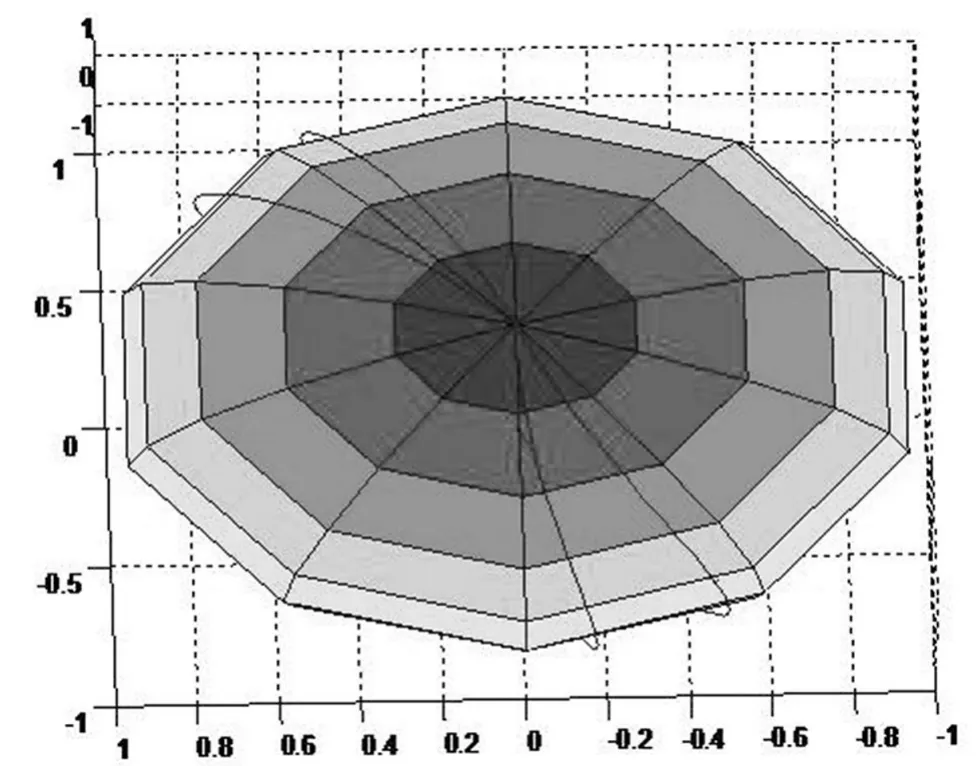
圖3 P點的綜合運動軌跡圖
本文利用展開輪推動鋼球轉角呈現正弦規律變化的趨勢,得出了鋼球運動變化的解析式(11)。為實現鋼球展開機構的優化,以此兩種特定的運動定量地研究鋼球的運動規律,建立一套更為準確、有效、簡便的數學工具是本文研究的重點。
為了驗證(11)式的正確同時利用MATLAB的數值計算功能和函數可視化功能,根據上面所提供的解析式得出球面上P點在不同時刻的運動軌跡圖如圖2所示。當球按照上述運動規律連續運動,直至完成一次全面展開,球面上P點的運動軌跡如圖3所示,可以看出時間化分得越小,P點的運動軌跡包絡成的曲線就是一個球面。
[1]蘇步青,華宣積,忻元龍.實用微分幾何引論[M].北京:科學出版社,1986.
[2]J.B.Marion.質點與系統的經典動力學[M].北京:高等教育出版社,1985.

