整體設計、自主探究、拓展思維
——等腰三角形概念及性質探究的教學實錄與說明

☉浙江省舟山南海實驗初中 張宏政

整體設計、自主探究、拓展思維
——等腰三角形概念及性質探究的教學實錄與說明

☉浙江省舟山南海實驗初中 張宏政

2014年9月25日，學校教研組要筆者開設一堂組內觀摩課，借此來一起研究“學為中心”理念下數學課堂的組織形態問題.按照教學進度是上浙教版八上教材第二章特殊三角形中第2節等腰三角形的概念.但筆者在仔細研讀教材后，對教學內容進行了重組設計，并取得了較好的課堂教學效果.現將它整理出來，以饗讀者，也歡迎廣大同仁批評指正.

一、目標定位與學情分析

1.教學目標

（1）通過分類理解等腰三角形的概念，并能正確識別；

（2）探索并證明等腰三角形的性質；

（3）應用等腰三角形的性質解決一些簡單的幾何證明問題.

2.教學重點

等腰三角形的概念與性質探索是本節課的重點，其中性質證明是本節課的難點.

3.學情分析

筆者任教的八（1）班是年段10個平行班中的1個.我校從2002年開始就對八、九年級施行數學、科學間的A、B班分層教學.本次開課的是八（1）班的A班25名學生，七年級（下）期末數學年段平均分為85.88分，八（1）班的平均分為87.56分，而A班學生的平均分為92.84分.一年多來的數學學習與熏陶，這些學生對數學的學習興趣普遍濃厚，思維活躍，學習能力也較強，同時，對幾何的整體框架與基本研究思路已有了初步的了解，小學里對等腰三角形的知識也有所涉及，這就為筆者整合教材提供了堅實的基礎.

二、課堂實錄

1.開門見山，直指概念

（請學生朗讀）定義、性質、判定——幾何研究的三個內容；觀察、猜想、論證——幾何學習的基本途徑.

師：大家都知道，幾何是一門直觀與邏輯相結合的學科.下面就讓我們從觀察開始進入到今天的學習之中（出示圖1與問題）.

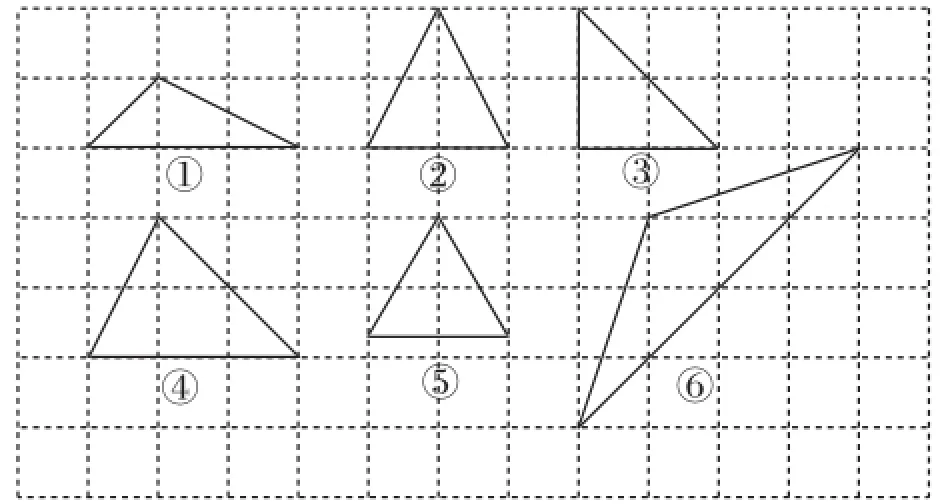
圖1

觀察圖1中的6個三角形，你認為是否存在特殊的三角形.若存在，是哪幾個？特殊在什么地方？

生1：我認為②③⑥是一類，它們都有兩條邊相等；⑤也是一類，它的三邊相等.

師：大家都同意他的觀點嗎？

生2：三邊相等其實也可以包含在兩邊相等之內，所以②③⑤⑥都可以算一類.

師（看到個別學生還有一點疑惑）：哦，看來個別學生還有疑惑.舉個例子吧，今天有很多老師來聽課，那么聽課的女老師是老師嗎？

生眾：那當然是的.

師：所以，三邊都相等的三角形包含在兩邊相等的三角形中.好，為了研究方便，請給這一類三角形取個名字，并且下一個定義吧.

生眾：叫等腰三角形吧.它的定義是：至少有兩邊相等的三角形叫等腰三角形.

師：非常好，這樣三角形按邊分類就是：

下面我們來了解等腰三角形的一些概念（PPT呈現）.

如圖2所示，已知△ABC中，AB=AC，則△ABC就是等腰三角形.

等腰三角形中，相等的兩邊叫做腰，另一邊叫做底邊.

兩腰的夾角叫做頂角，腰和底邊的夾角叫做底角.

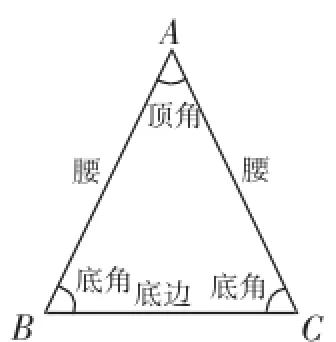
圖2

師：大家是否理解了這些概念呢？讓我們從問題解決中來證實.

做一做：

（1）如圖3，點D在AC上，AB=AC，AD= BD.你能在圖中找到幾個等腰三角形？說出每個等腰三角形的腰、底邊和頂角.

生3：有兩個，分別是△ABC與△ABD.△ABC的腰是AB和AC，底邊是BC，頂角是∠A；△ABD的腰是AD和BD，底邊是AB，頂角是∠ADB.

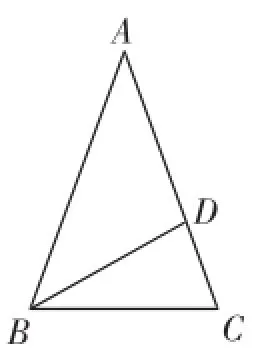
圖3

師：這位同學回答得怎樣？別的同學是否有異議.生眾：回答正確.

師：同學們理解得都很好，圖中的△BDC并沒有條件支撐，故不能想當然地認為它也是等腰三角形.請看第（2）題.

（2）已知等腰三角形一邊的長為3，另一邊的長為5，求它的周長.

生4：若腰長為3，則底邊長為5，于是周長=3+3+5= 11；若腰長為5，則底邊長為3，于是周長=5+5+3=13.

師：哦，懂得用分類討論來解決問題，非常不錯.那把題目變一變又如何呢？

（3）已知等腰三角形一邊的長為3，另一邊的長為7，則它的周長又為多少？

生5：周長為17.當三邊為7，7，3時，周長為17；當三條線段長分別為3，3，7時，因為3+3＜7，所以不能組成三角形.

師：看來，就算是同種類型的問題，也要充分考慮條件不同所帶來的變化.下面就讓我們一起來研究等腰三角形的性質吧.

2.操作實踐，自主探究

猜想、驗證、證明：

如圖4，已知△ABC中，AB=AC.

（1）通過觀察，你認為等腰三角形有哪些性質？

生眾：∠B=∠C.（師板書：猜想∠B=∠C）

（2）請你通過操作驗證你的猜想.

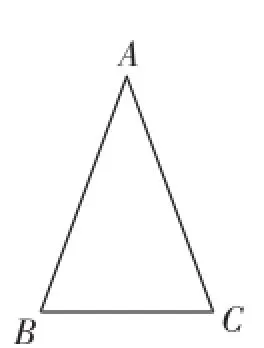
圖4

（3）由操作方法，你是否想到了證明的思路？請你完成證明.

給每個小組發兩張全等的等腰△ABC紙片，操作前提示學生：若用一張紙片如何驗證，用兩張紙片又該如何驗證？約7分鐘后，小組代表匯報.

生6：用一張紙片，可以通過對折驗證.若用兩張紙片，可以把第一個三角形的∠B與第二個三角形的∠C重疊在一起驗證.

師：那你們組是如何證明的呢？

生6：如圖5，作∠A的平分線AD，則∠BAD=∠CAD.又因為AB=AC，AD=AD，故△ABD≌△ACD，所以∠B=∠C.如圖6，因為AB=AC，AC=AB，BC=CB，所以△ABC≌△ACB，所以∠B=∠C.

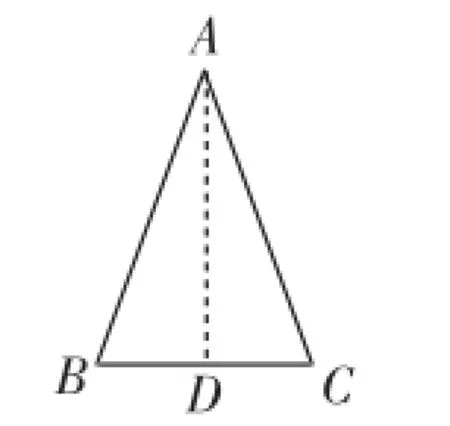
圖5

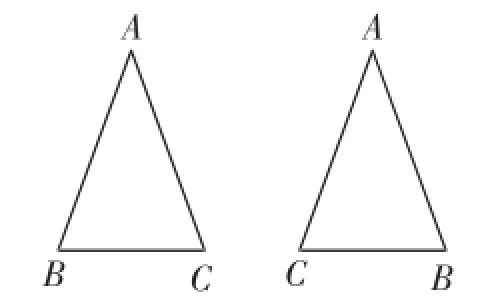
圖6

生7（補充道）：也可以用SAS證明，因為還有∠A=∠A.

師：很不錯，學習數學就是學習轉化.兩種方法都是把證明角相等的問題轉化成證明全等三角形的問題，可謂殊途同歸.但第一種是把三角形分割成一對全等三角形，第二種則是無中生有，復制出一對全等三角形，真是條條大道通羅馬啊.那么，通過第一種證明還能得到哪些副產品？

生8：因為△ABD≌△ACD，所以BD=CD，∠BDA=∠CDA=90°，所以等腰三角形頂角的平分線、底邊上的高線與中線互相重合.

生9：因為△ABD≌△ACD，所以等腰三角形還是軸對稱圖形，角平分線AD所在直線是它的對稱軸.

師：非常好，這樣我們就從邊、角、重要線段、整體這四個視角分別詮釋了等腰三角形的定義與性質（板書……）.下面我們把這些性質來鞏固一下.

3.鞏固新知，內化方法

用一用：

如圖7，已知△ABC中，AB=AC，D為BC的中點，過點D作DE⊥AB于點E，DF⊥AC于點F.求證：DE=DF.

生10：因為AB=AC，所以∠B=∠C.因為D為BC的中點，所以BD=CD.又因為DE⊥AB，DF⊥AC，所以∠BED=∠DFC=90°，所以△BED≌△CFD，所以DE=DF.

師：利用性質來證明全等，思路很清晰，掌聲鼓勵一下.還有不同方法嗎？

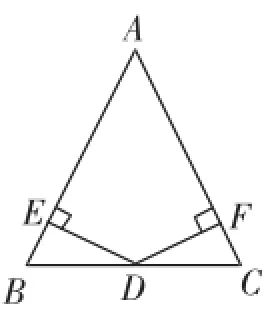
圖7

生11：如圖8，連接AD，因為AB= AC，D為BC的中點，所以AD平分∠BAC.又因為DE⊥AB，DF⊥AC，所以DE=DF（角平分線上的點到角兩邊的距離相等）.

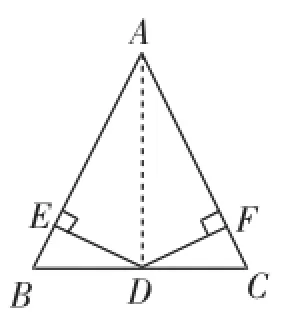
圖8

師：由距離相等聯想角平分線性質，進而聯想等腰三角形三線合一的性質，真不錯.看來，思路決定出路啊.還有不同的方法嗎，由兩條高線你還能聯想到什么？

生12：如圖8，連接AD，因為D為BC的中點，所以S=S.因為DE⊥AB，DF⊥AC，所以AB·DE=AC·

△ABD△ACDDF.因為AB=AC，所以DE=DF.

師：面積法在幾何證明中有時會有很大用處，值得同學們好好品味.同時也告訴我們，具備良好的知識結構是多么的重要.下面讓我們來練一練.

（1）如圖9，已知AB=AC，BD=CD，求證：①∠ABD=∠ACD；②AD⊥BC.

生13：①因為AB=AC，BD=CD，AD=AD，所以△ABD≌△ACD，所以∠ABD=∠ACD.

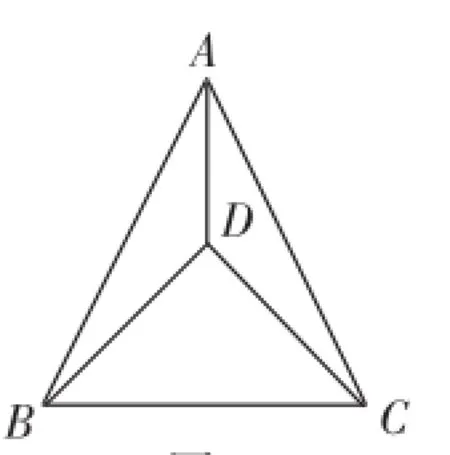
圖9

②因為△ABD≌△ACD，所以∠BAD=∠CAD.因為AB=AC，所以AD⊥BC.

師：還有不同方法嗎？

生14：①的證明還可以由AB=AC得到∠ABC=∠ACB，由BD=CD得到∠ABD=∠ACD，再分別相減得到∠ABD=∠ACD，從而問題得證.

師：從上面的證明分析，大家已經明白了證明邊（角）相等的方法，既可以考慮兩個三角形全等，也可以考慮用同一個三角形等邊對等角的方法，關鍵是要認真分析題中的條件.讓我們再看下面的問題.

（2）如圖10，已知△ABC中，AB= AC，BD、CE分別為AC、AB邊上的高線，求證：BD=CE.

生15：因為BD、CE分別為AC、AB邊上的高線，所以∠AEC=∠ADB= 90°.又因為AB=AC，∠A=∠A，所以△AEC≌△ADB，故BD=CE.

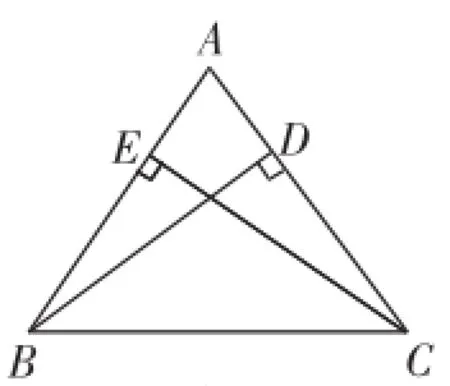
圖10

師：能用△BEC≌△CDB來證明嗎？

生15（思考片刻后）：可以的，因為∠BEC=∠CDB= 90°，BC=CB，由AB=AC可得到∠ABC=∠ACB.

師：看來大家對全等的證明方法理解得非常好，還有不同方法嗎？

△ABCAC·BD，又AB=AC，所以BD=CD.

師：哦，如此說來，面積法也應該成為求證線段相等的基本方法，大家同意吧.同時，同學們平時在解題的過程中不應該僅僅滿足于完成任務，而應該通過解題來優化思維，總結經驗，提煉方法.下面大家就來一起歸納一下本課學習的知識與方法吧……（余略）

三、對教學設計及課堂實踐的思考

1.對教材內容重組的認識

先讓我們看看教材的安排，等腰三角形從概念到性質共設計3個課時進行探索，其中第1課時是了解等腰三角形的概念，掌握等腰三角形的軸對稱性（基于操作基礎之上的感性認識）并應用，第2課時先探究等腰（等邊）三角形角的性質，第3課時再探索等腰三角形的三線合一性質.同時，教材對等腰三角形的概念是通過“在小學我們已經學過，有兩邊相等的三角形是等腰三角形”這樣一段文字直接給出的，缺少為什么要研究的動因，而教材對性質探究的安排，又人為割裂了知識發生發展的過程與相互聯系，按照這樣的設計展開教學，容易讓學生只見樹木，不見森林，難以對幾何的基本研究套路形成清晰而完整的認知.就像欣賞一首優美的曲子時總是在動聽處嘎然而止，極不自然.于是便有了本課一氣呵成的重組：從若干三角形中尋求特殊（按邊特殊分類）→定義等腰三角形（提出課題）→研究性質→觀察猜想→驗證解釋→分析證明→鞏固運用→歸納小結.這樣的設計，遵循了學生的認知規律，既為后面直角三角形（按角特殊分類）的教學進行了鋪墊，也為今后讓學生自主研究特殊平行四邊形奠定了必要的方法基礎.

2.對等腰三角形性質探究及內化設計的說明

本課的教學重點是等腰三角形性質的探究，因此，如何讓學生自主發現證明思路就是本課的關鍵事件.事實上，多年的教學實踐經驗告訴筆者，第一種證明思路學生容易想到，而第二種證明思路學生確實不容易想到.于是，本設計借用了兩張全等的等腰三角形紙片，讓學生在自主驗證猜想的過程中發現兩種證明的思路，并在后面的方法對比環節讓學生從思想方法的高度體驗兩種證明思路的本質是一致的.值得一提的是，這樣的設計是可行也是有效的，學生在后面探究勾股定理逆定理的時候，就比較自然地想到了復制一個直角三角形進行證明.

數學教學的本質是思維活動的教學，這就要在課堂上給學生留下充裕的思考時間.而本課的容量又很大，為克服這對矛盾，就必須在問題的設計上做到典型、精煉且解法多樣，能滿足學生鞏固知識，領會方法的目標.于是筆者僅安排一道內涵豐富的例題進行鞏固，用兩個習題進行內化.課堂實踐表明，學生的思維空前活躍，有效達成了教學目標.

3.對課堂教學組織的思考

本課觀摩的初衷是研究“學為中心”理念下課堂教學的基本組織形態，這也是目前課堂教學變革的熱門話題.但不可否認的是，目前的一些課堂變革存在庸俗化、功利化的傾向.特別是一些不管學科特點的模式化做法從一個極端走向了另一個極端.這里，筆者無意去評論這些現象.只是從數學教育的本質，學生思維發展的目標思考，我們的數學課堂既要不斷提高學生學習的自覺性，也要有效發揮教師啟發、引領的作用；既要重視學生的獨立思考，也要給學生的合作交流、思維碰撞提供機會.本課的實踐過程正是以此為指導思想而展開，探究時放開，交流時等待，介入時引導，自主時明確要求.以知識的發生發展為線索，以學生鞏固知識、內化方法、體驗思想作為教學的根本與歸宿.正所謂，一節好課，其深厚之處一定在于教師對教學內容獨到的解讀，在于對學生精準的理解，在于對教育理念的深刻把握.故此，教學之美一定是在調動教與學雙方力量的過程中產生的.它既是規律之美，也是藝術之美.

1.義務教育教科書·數學（八年級上冊）［M］.杭州：浙江教育出版社，2013.

2.章建躍.探究數學規律，造就數學名師［J］.中國數學教育（初中版），2011（1-2）.

3.裴光亞.教學的智慧［J］.中學數學教學參考（下），2008（4）.

4.浦敘德，謝潔紅.從知識整體性視角設計主問題引領課堂教學［J］.中學數學（上），2014（10）.

5.余慧娟.教學改革的方向性思考［J］.人民教育，2011（1）.