追求邏輯連貫的數(shù)學教學
——以“多邊形內(nèi)角和”教學為例

☉江蘇省徐州高級中學 劉 華

追求邏輯連貫的數(shù)學教學
——以“多邊形內(nèi)角和”教學為例

☉江蘇省徐州高級中學 劉 華

我們知道，初中平面幾何內(nèi)容主要來源于《幾何原本》，前后知識的邏輯連貫是其特色.筆者最近觀摩了一次同課異構教學活動，開課課題是“多邊形內(nèi)角和”，本文記錄兩種不同風格的教學設計，并給出解讀和反思，與同行研討.

一、兩種教學設計

（一）第一種教學設計

教學環(huán)節(jié)1：創(chuàng)設情境，引入新課.

問題1：某個多邊形所有的角加起來等于它的外角和，那么該多邊形是幾邊形？小明僅用幾分鐘就解決了問題，你能嗎？

問題2：用四塊大小、形狀完全相同的四邊形可拼成一塊無空隙的紙板，你知道為什么嗎？

設計意圖：這樣一開始設疑，學生很容易發(fā)問，這個多邊形是幾邊形呢？用四塊大小、形狀完全相同的四邊形可拼成一塊無空隙的紙板，為什么會產(chǎn)生這種效果呢？從而可調(diào)動學生的學習興趣和注意力，創(chuàng)設恰當?shù)慕虒W情境.

教學環(huán)節(jié)2：合作交流，探索新知.

（1）問題：三角形的內(nèi)角和等于多少度？外角和等于多少度？長方形的內(nèi)角和等于多少度？正方形的內(nèi)角和等于多少度？

（2）問題：任意四邊形的內(nèi)角和等于多少度呢？你是怎樣得到的？你有幾種方法？

（3）學生思考并分組討論，教師深入小組參與活動，指導傾聽學生交流.

（4）學生分組選代表展示小組的探索成果，師生共同進行評判，對學生找到的不同的方法及時給予肯定.

設計意圖：學生可能找到以下幾種方法：“量”——先測量四邊形四個內(nèi)角的度數(shù)，然后求四個內(nèi)角的和；“拼”——把四邊形的四個內(nèi)角剪下來，然后拼在一起形成一個周角；“分”——通過添加輔助線的方法，把四邊形割成三角形.

教師在學生展示完后提問：在“量”“拼”“分”這幾種方法中，哪種方法簡單又相對準確？我們剛才找到了幾種作輔助線的方法，它們的共同點是什么？

教學環(huán)節(jié)3：自主探究，得出結論.

（1）問題：用剛才類似的方法，你能算出五邊形、六邊形、七邊形的內(nèi)角和嗎？

（2）問題：依次類推，n邊形的內(nèi)角和等于多少度呢？

設計意圖：讓學生自己歸納總結，得出n邊形內(nèi)角和公式為（n-2）·180.

教學環(huán)節(jié)4：應用新知，嘗試練習.

（1）想一想：如果一個四邊形的對角互補，那么另一組對角有什么關系？為什么？

（2）算一算：四邊形、五邊形、六邊形以及n邊形的外角和呢？

教學環(huán)節(jié)5：歸納總結，形成體系.

從以下幾方面引導學生進行小結.

（1）現(xiàn)在你能解決情境中的兩個問題嗎？

（2）這節(jié)課你學習了哪些知識和方法？你有什么收獲？

（二）第二種教學設計

教學環(huán)節(jié)1：回顧舊知，猜想新知.

提問：回顧三角形的內(nèi)角和和外角和，猜想多邊形的內(nèi)角和與外角和.

預設與引導：三角形的內(nèi)角和等于180°，外角和等于360°.如圖1，可以通過作平行線，平移∠1、∠2、∠3到三角形的一個頂點處，得到一個周角，說明∠1＋∠2＋∠3＝360°.例如過點C作CD∥AB.

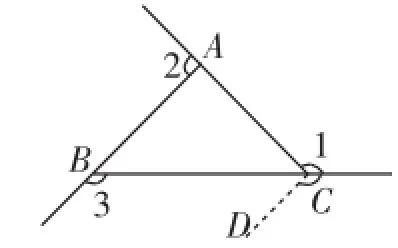
圖1

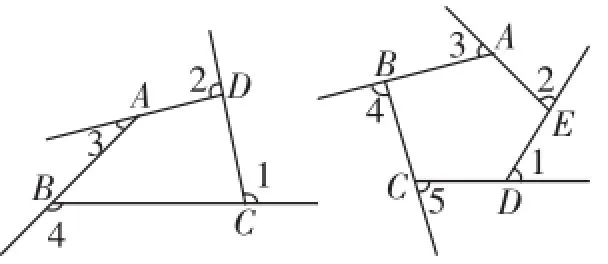
圖2

當邊數(shù)增加時（如圖2），多邊形的內(nèi)角個數(shù)、外角個數(shù)隨之增加，多邊形的內(nèi)角和和外角和會隨之發(fā)生變化嗎？

（同學們自己思考、探究、猜想、伴以小組討論）

教學環(huán)節(jié)2：全班交流研究的方法和成果.

（1）先研究內(nèi)角和，后研究外角和.

以四邊形為例.

怎樣研究？——作輔助線，將原多邊形分成若干個三角形（如圖3）.

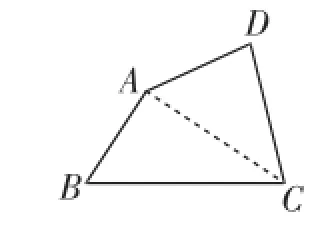
圖3

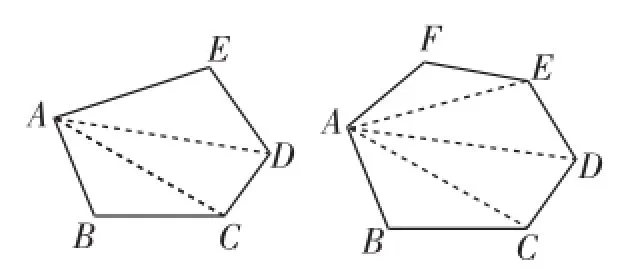
圖4

方法1：過四邊形ABCD的一個頂點作對角線，再由四邊形擴展到n邊形（如圖4）.歸納出：

過一個頂點所作的對角線條數(shù)等于（n-3）；

過一個頂點作對角線，將原n邊形分成的三角形的個數(shù)為（n-2）.

n邊形的內(nèi)角和等于（n-2）·180°.

方法2：在多邊形的邊上、形內(nèi)或形外任取一點O（如圖5），與各頂點連接，運用“三角形內(nèi)角和等于180°”同樣可得上述結論.

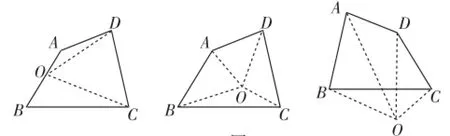
圖5

由多邊形內(nèi)角和公式和多邊形外角定義，易得：多邊形的外角和等于360°.

（2）先研究外角和，后研究內(nèi)角和.

如圖6，過C作CE∥DA，CF∥AB.則∠DCE＝∠2，∠ECF＝∠3，∠FCM＝∠4.

由周角定義可得：∠1＋∠2＋∠3＋∠4＝360°.

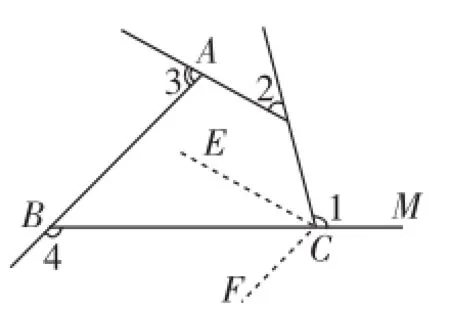
圖6

即：n邊形的外角和等于360°.

根據(jù)多邊形外角定義及“多邊形的外角和等于360°”，易得多邊形的內(nèi)角和公式：多邊形的內(nèi)角和等于（n-2）·180°.

師生總結：

當多邊形的邊數(shù)變化時，多邊形的內(nèi)角和隨之變化，為變量，而外角和卻始終不變，為一個常量360°；

在研究變化過程中的數(shù)量關系時，可從變量入手，也可從不變的量入手研究；

教學環(huán)節(jié)3：練習鞏固.

練習1：（改編自教材習題）如圖7，五邊形ABCDE中，必須已知怎樣的條件方可求得∠E的度數(shù)？

預設意圖：學生自己思考編題、解題.教師預設如下.

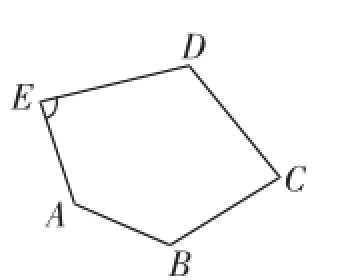
圖7

（1）已知其他4個角的度數(shù)（∠A＝135°，∠B＝120°，∠C＝60°，∠D＝150°）；

（2）已知與∠E相鄰的外角的度數(shù)或它們之間的數(shù)量關系.

練習2：一個多邊形的各內(nèi)角都等于120°，它是幾邊形？

變式：根據(jù)多邊形的外角與相鄰內(nèi)角的互補關系，正多邊形的各個內(nèi)角相等，外角也相等.還可編出哪些求邊數(shù)的問題？

如：一個正多邊形的內(nèi)角和等于外角和的4倍，求邊數(shù)；

一個多邊形的內(nèi)角和比它的外角和的5倍少180°，求邊數(shù).

教學環(huán)節(jié)4：小結.（略）

二、解讀和反思

1.第一種設計的主要立意

首先是教材處理上較有特色，比如將教材中的例題改編成練習，由學生自己嘗試解答；將教材中求六邊形的外角和，改為練習中的“算一算”，先讓學生求四邊形的外角和，再探索五邊形、六邊形及n邊形的外角和.這樣處理主要是體現(xiàn)學生的自主性，使學生變“被動”為“主動”.教學形式上，將不少練習采取分組競賽的形式合作完成，使學生產(chǎn)生強烈的學習興趣，追求較好的課堂氣氛.

2.第二種設計的主要立意

開課階段，教者首先從學生實際出發(fā)，引導學生回顧三角形內(nèi)、外角和定理及其證明方法，在教師設置的問題引領下，使學生選擇適當?shù)难芯坎呗裕箤W生認識到只要類比三角形的內(nèi)角和定理及外角和的證明方法，通過添加輔助線，將其轉(zhuǎn)化為三角形就可以解決新問題.這樣做不僅讓學生再次體會類比和擴展方法的使用，以及把復雜問題化為簡單問題，化未知為已知的思維方法，而且使學生體驗到事物的“對立和統(tǒng)一”“矛盾與轉(zhuǎn)化”的規(guī)律.

3.兩種教學設計的對比

可以發(fā)現(xiàn)，第一種設計只是對教材的亦步亦趨、小修小改，屬于尊重教材、嚴守教材的一種教學取向，課堂容量有限，表面上學生活動形式多樣、課堂氣氛活躍、有大量展示，但是數(shù)學的思維活動卻不能與第二種教學設計相比.在第二種教學設計的課堂上，我們注意到課中教者巧妙地把同類的問題放在一起讓學生去感受、去體會、去總結；引導學生從問題個性中探求共性，尋求變異，多角度、多層次去構思、延伸、拓展，這樣引導學生自主探究，有利于激活學生的思維，使學生的學力得到有效鍛煉和提高，是一節(jié)更有數(shù)學味兒的課堂，也是我們應該追求的前后一致、邏輯連貫的數(shù)學教學取向.

1.李庾南.自學·議論·引導教學論［M］.北京：人民教育出版社，2013.

2.章建躍，陳向蘭.數(shù)學教育之取勢明道優(yōu)術［J］.數(shù)學通報，2014（10）.

3.中華人民共和國教育部制定.義務教育數(shù)學課程標準（2011年版）［M］.北京：北京師范大學出版社，2012.

4.【日】佐滕學.21世紀學校改革的方向［J］.人民教育，2014（1）.

5.馬立平，著.小學數(shù)學的掌握和教學［M］.李士锜，吳穎康，等，譯.上海：華東師范大學出版社，2011.